1.2 矩形的性质与判定 同步练习(解析版)
文档属性
| 名称 | 1.2 矩形的性质与判定 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 00:00:00 | ||
图片预览



文档简介
初中数学北师大版九年级上学期 第一章 1.2 矩形的性质与判定
一、单选题
1.下列结论中,矩形具有而菱形不一定具有的性质是(?? )
A.?内角和为360°???????????? ?????B.?对角线互相平分?????????? ???????C.?对角线相等?????????? ???????D.?对角线互相垂直
2.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( ??)
A.?AB=CD??????????????????????????????B.?AB=BC??????????????????????????????C.?AC⊥BD??????????????????????????????D.?AC=BD
3.对于任意的矩形,下列说法一定正确的是(?? )
A.?对角线垂直且相等 B.?四边都互相垂直 C.?四个角都相等 D.?是轴对称图形,但不是中心对称图形www.21-cn-jy.com
4.如图,矩形ABCD的对角线交于点O.若∠BAO=55°,则∠AOD等于(??? )
A.?110°????????????????????????????????????
B.?115°????????????????????????????????????
C.?120°????????????????????????????????????
D.?125°
5.如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为(??? )
A.??????????????????????????????????????????
B.?2?????????????????????????????????????????
C.??????????????????????????????????????????
D.?6
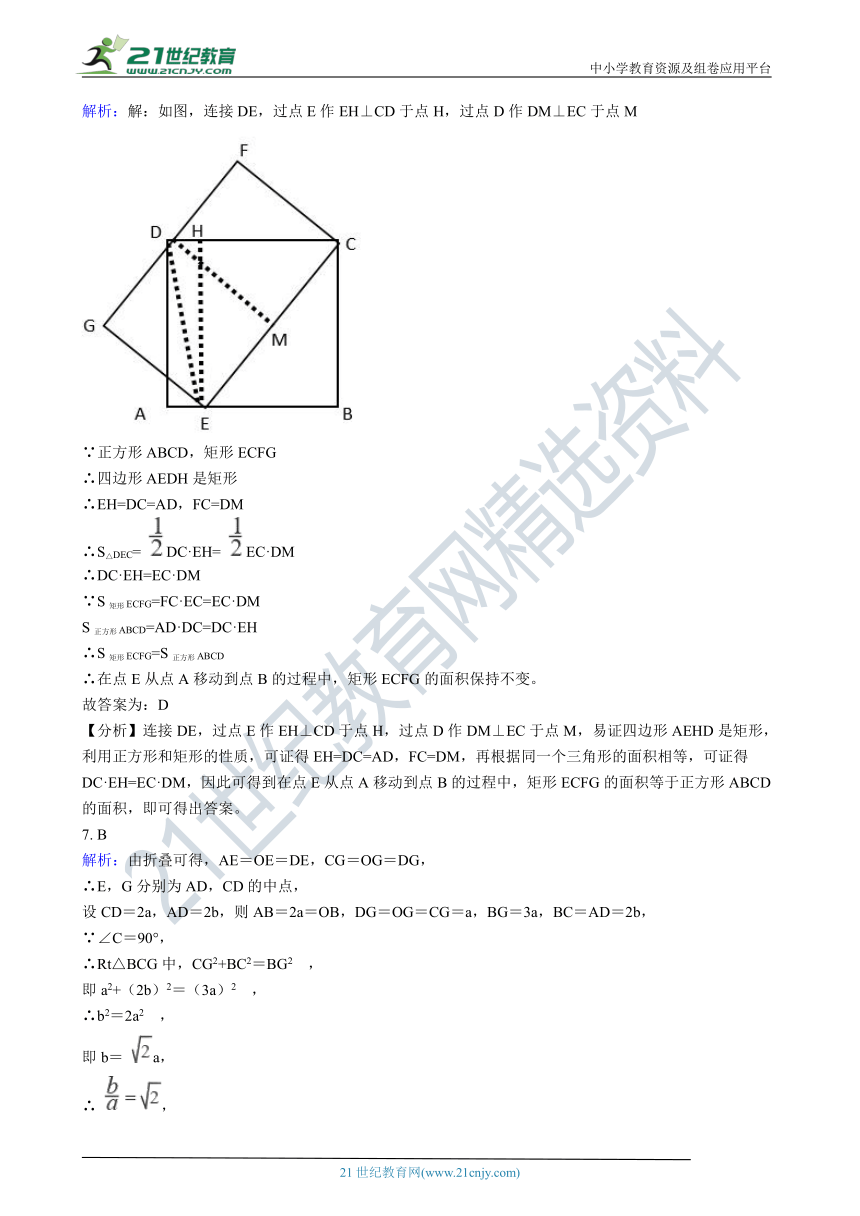
6.正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( ??) 21·cn·jy·com
A.?先变大后变小???????????????????????
B.?先变小后变大???????????????????????
C.?一直变大???????????????????????
D.?保持不变
7.将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则 的值为(?? )
A.?????????????????????????????????????????
B.?????????????????????????????????????????
C.?????????????????????????????????????????
D.?
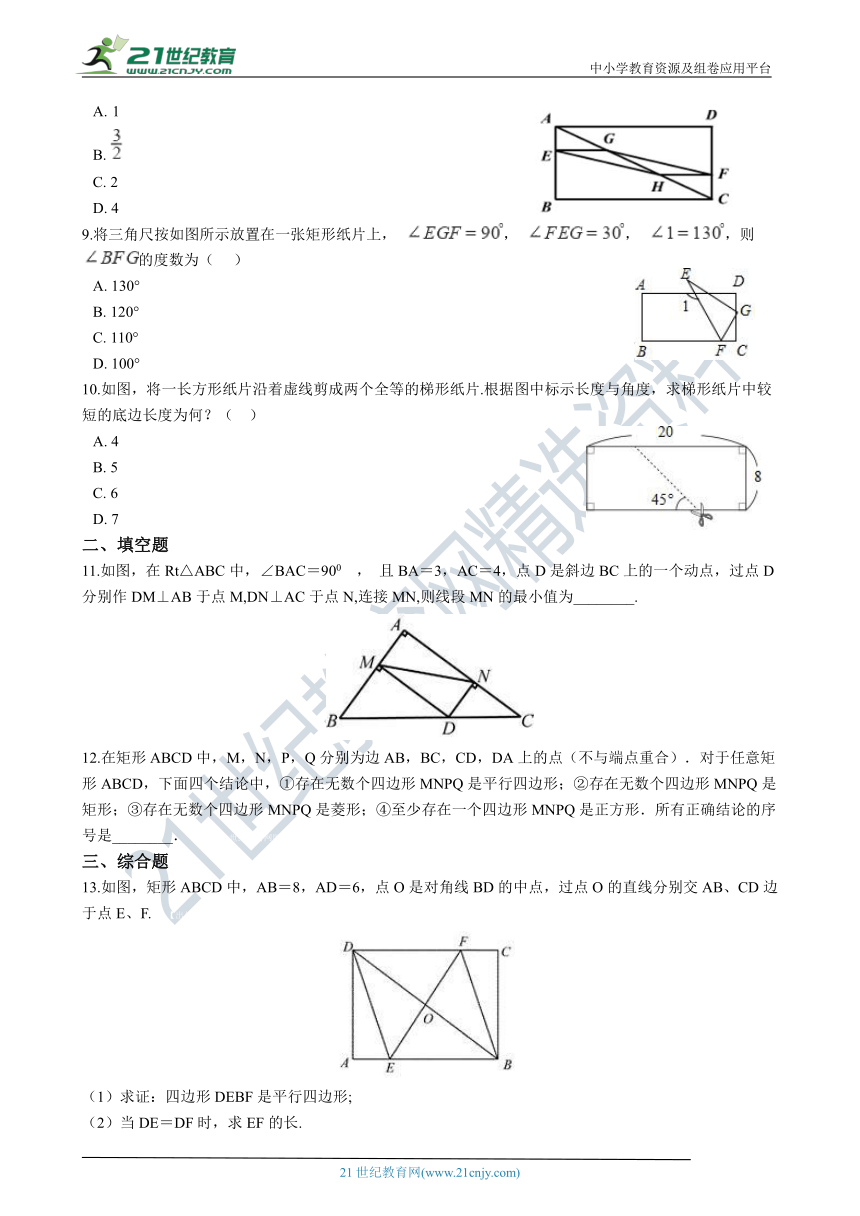
8.如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为(??? ) 2-1-c-n-j-y
1??????????????????????????????????????????
B.????????????????????????????????????????????
C.?2??????????????????????????????????????????
D.?4
9.将三角尺按如图所示放置在一张矩形纸片上, , , ,则 的度数为(??? )
A.?130°????????????????????????????????????
B.?120°????????????????????????????????????
C.?110°????????????????????????????????????
D.?100°
10.如图,将一长方形纸片沿着虚线剪成两个全等的梯形纸片.根据图中标示长度与角度,求梯形纸片中较短的底边长度为何?(?? ) 【来源:21cnj*y.co*m】
A.?4???????????????????????????????????????????
B.?5???????????????????????????????????????????
C.?6???????????????????????????????????????????
D.?7
二、填空题
11.如图,在Rt△ABC中,∠BAC=900 , 且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为________.
12.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是________. 21世纪教育网版权所有
三、综合题
13.如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F. 【出处:21教育名师】
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求EF的长.
14.已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)如图1,求证:AE=CF;
(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的 . 【版权所有:21教育】
15.如图,在平面直角坐标系中,O是原点,点A在x轴的负半轴上,点B在y轴的正半轴上,AO=2OB,且线段OB的长是方程x2-2x-8=0的一个根. 21教育名师原创作品
(1)求直线AB的函数解析式.
(2)将△ABD绕点O逆时针方向旋转90°得到△EDO,直线ED交线段AB 于点C,点F是直线CE上一点,分别过点E、F作x轴和y轴的平行线交于点G,将△EFG沿EF折叠,使点G的对应点落在坐标轴上,求点F的坐标.
(3)在(2)的条件下,点M是DO中点,点N、P、Q在直线BD或者y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请利用备用图画出示意图并直接写出点P的坐标;若不存在,请说明理由.
答案解析部分
一、单选题
1. C
解析:A、菱形、矩形的内角和都为360°,故不符合题意;
B、对角互相平分,菱形、矩形都具有,故不符合题意;
C、对角线相等菱形不具有,而矩形具有,故符合题意
D、对角线互相垂直,菱形具有而矩形不具有,故不符合题意,
故答案为:C.
【分析】所有的四边形的内角和都是360°;所有的平行四边形的对角线都互相平分;菱形、矩形都是四边形且都是平行四边形,故可判断A,B都不符合题意;矩形的对角线相等,但不垂直;菱形的对角线互相垂直,但不相等,故可判断C符合题意,D不符合题意。21教育网
2. D
解析:四边形的对角线互相平分,即可得出四边形为平行四边形 添加AC=BD,可根据矩形判定定理对角线相等的平行四边形是矩形,判定四边形为矩形。
故答案为:D
【分析】根据矩形的判定定理可添加条件。
3. C
解析: A.矩形的对角线相等,但不垂直,故此选项不符合题意;
B、矩形的邻边都互相垂直,对边互相平行,故此选项不符合题意;
C.矩形的四个角都相等,符合题意;
D.矩形是轴对称图形,也是中心对称图形,故此选项不符合题意.
故答案为:C. 【分析】矩形的四个角都相等且都等于90°,矩形的对边相等、对角线相等,矩形是轴对称图形也是中心对称图形,据此逐一判断即可.
4. A
解析:∵四边形ABCD是矩形,∴AC=BD,OA=OB,∠OAB=∠OBA=55°,∠AOD=∠OAB+∠OBA=55°+55°=110°. 故答案为:A
【分析】由矩形的对角线互相平分得,OA=OB,再由三角形的外角性质得到∠AOD等于∠OAB和∠OBA之和即可求解。
5. B
解析:由题意可得,大正方形的边长为 ,小正方形的边长为 ,
∴图中阴影部分的面积为: ,
故答案为:B. 【分析】根据正方形的性质可求出大正方形的边长及小正方形的边长,图中阴影部分利用平移可得一个矩形,利用矩形的面积公式计算即可.
6. D
解析:解:如图,连接DE,过点E作EH⊥CD于点H,过点D作DM⊥EC于点M
∵正方形ABCD,矩形ECFG
∴四边形AEDH是矩形
∴EH=DC=AD,FC=DM
∴S△DEC= DC·EH= EC·DM
∴DC·EH=EC·DM
∵S矩形ECFG=FC·EC=EC·DM
S正方形ABCD=AD·DC=DC·EH
∴S矩形ECFG=S正方形ABCD
∴在点E从点A移动到点B的过程中,矩形ECFG的面积保持不变。
故答案为:D
【分析】连接DE,过点E作EH⊥CD于点H,过点D作DM⊥EC于点M,易证四边形AEHD是矩形,利用正方形和矩形的性质,可证得EH=DC=AD,FC=DM,再根据同一个三角形的面积相等,可证得DC·EH=EC·DM,因此可得到在点E从点A移动到点B的过程中,矩形ECFG的面积等于正方形ABCD的面积,即可得出答案。
7. B
解析:由折叠可得,AE=OE=DE,CG=OG=DG,
∴E,G分别为AD,CD的中点,
设CD=2a,AD=2b,则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=2b,
∵∠C=90°,
∴Rt△BCG中,CG2+BC2=BG2 ,
即a2+(2b)2=(3a)2 ,
∴b2=2a2 ,
即b= a,
∴ ,
∴ 的值为 。
故答案为:B。
【分析】由折叠的性质可得,AE=OE=DE,CG=OG=DG,设CD=2a,AD=2b,则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=2b,在Rt△BCG中,利用勾股定理建立方程求解得出a,b的关系进而即可求出答案。
8. C
解析:如图,延长FH交AB于点M,
∵BE=2AE,DF=2FC,AB=AE+BE,CD=CF+DF,
∴AE:AB=1:3,CF:CD=1:3,
又∵G、H分别是AC的三等分点,
∴AG:AC=CH:AC=1:3,
∴AE:AB=AG:AC,CF:CD=CH:CA,
∴EG//BC,FH//AD,
∴△AEG∽△ABC,△CFH∽△CDA,BM:AB=CF:CD=1:3,∠EMH=∠B,
∴EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,
∵四边形ABCD是矩形,AB=3,BC=6,
∴CD=AB=3,AD=BC=6,∠B=90°,
∴AE=1,EG=2,CF=1,HF=2,BM=1,
∴EM=3-1-1=1,EG=FH,
∴EG FH,
∴四边形EHFG为平行四边形,
∴S四边形EHFG=2×1=2,
故答案为:C。
【分析】如图,延长FH交AB于点M,根据线段之间的关系可以得出AE:AB=AG:AC,CF:CD=CH:CA,根据平行线分线段成比例定理的逆用得出EG//BC,FH//AD,根据平行于三角形一边的直线,截其它两边,所截的三角形与原三角形相似得出△AEG∽△ABC,△CFH∽△CDA,根据相似三角形对应边成比例得出EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,根据矩形的性质进而即可得出EG=2,HF=2,根据一组对边平行且相等的四边形是平行四边形判断出四边形EHFG为平行四边形,进而根据平行四边形面积的计算方法即可算出答案。21*cnjy*com
9. C
解析:∵ , ,
∴ ,
又∵ , ,
∴ ,
∴ 。
故答案为:C。
【分析】根据矩形的对边平行得出AD∥BC,根据二直线平行,同旁内角互补得出∠BFE的度数,根据三角形的内角和得出∠EFG的度数,进而根据角的和差,由∠BFR+∠EFG=∠BFG算出答案。
10. C
解析:过F作FQ⊥AD于Q,
则∠FQE=90°,
∵四边形ABCD是长方形,
∴∠A=∠B=90°,AB=DC=8,AD∥BC,
∴四边形ABFQ是矩形,
∴AB=FQ=DC=8,
∵AD∥BC,
∴∠QEF=∠BFE=45°,
∴EQ=FQ=8,
∴AE=CF= ×(20-8)=6,
故答案为:C.
【分析】过F作FQ⊥AD于Q,很容易判断出四边形ABFQ是矩形,根据矩形的性质得出AB=FQ=DC=8,进而判断出△EFQ是等腰直角三角形,根据等腰直角三角形的性质得出EQ=FQ=8,从而根据线段的和差即可算出答案。2·1·c·n·j·y
二、填空题
11. (或2.4)
解析:如图,连接AD. ∵ ∠BAC=90°,且BA=3,AC=4 , ∴BC=5, ∵ DM⊥AB于点M,DN⊥AC于点N ,∠BAC=90°, ∴四边形AMCN是矩形, ∴MN=AD, 由垂线段最短可得CP⊥AB时,线段MN的值最小, 此时,△ABC的面积=, , 解得AD=即 线段MN的最小值为 : 故答案为: 【分析】首先根据UGG多了算出BC的长,然后判断出四边形AMCN是矩形,根据矩形的对角线相等得出MN=AD,由垂线段最短可得CP⊥AB时,线段MN的值最小,然后滚局三角形的面积法即可算出AD的长,从而得出答案。21·世纪*教育网
12. ①②③
解析:①如图,∵四边形ABCD是矩形,连接AC,BD交于O,
过点O直线MP和QN,分别交AB,BC,CD,AD于M,N,P,Q,
则四边形MNPQ是平行四边形,
故当MQ∥PN,PQ∥MN,四边形MNPQ是平行四边形,
故存在无数个四边形MNPQ是平行四边形;故正确;
②如图,当PM=QN时,四边形MNPQ是菱形,故存在无数个四边形MNPQ是矩形;故正确;
③如图,当PM⊥QN时,存在无数个四边形MNPQ是菱形;故正确;
④当四边形MNPQ是正方形时,MQ=PQ,
则△AMQ≌△DQP,
∴AM=QD,AQ=PD,
∵PD=BM,
∴AB=AD,
∴四边形ABCD是正方形与任意矩形ABCD矛盾,故错误;
故答案为:①②③.
【分析】分别根据矩形,平行四边形,菱形的判定定理以及性质得到答案即可。
三、综合题
13. (1)证明:∵四边形ABCD是矩形
∴AB∥CD
∴∠DFO=∠BEO,
又因为∠DOF=∠BOE,OD=OB
∴△DOF≌△BOE∴DF=BE
又因为DF∥BE,
∴四边形BEDF是平行四边形 (2)解:∵DE=DF,四边形BEDF是平行四边形
∴ BEDF是菱形∴DE=BE,EF⊥BD,OE=OF
设AE=x,则DE=BE=8-x
在Rt△ADE中,根据勾股定理,有AE2+AD2=DE2
∴x2+62=(8-x)2解之得:x=
∴DE=8- =
在Rt△ABD中,根据勾股定理,有AB2+AD2=BD2
∴BD= ∴OD= BD=5,
在Rt△DOE中,根据勾股定理,有DE2-OD2=OE2 ,
∴OE=
∴EF=2OE=
解析:(1)抓住题给条件 点O是对角线BD的中点,证明三角形全等,得对应边相等。再利用平行四边形判定定理,一组对边平行且相等是平行四边形。 (2)因为邻边相等的平行四边形是菱形,由菱形的性质知,四边都相等,在Rt△ADE中,设AE=x, 利用勾股定理列关系式解出x. x值解出,后面就容易了,根据菱形性质对角线互相垂直平分,用勾股定理即可求解。21cnjy.com
14. (1)证明: ∵四边形ABCD是矩形 ∴AB∥CD,AB=CD ∴∠ABE=∠CDF ∵AE⊥BD,CE⊥BD ∴∠AEB=∠CFD=90° 在△ABE和△CDF中 ∴△ABE≌△CDF(AAS) ∴AE=CF (2)解: ∵△ABE≌△CDF ∴BE=DF ∴S△AFD=S△ABE=S△FDC=S△BEC ∵ ∠ADB=30° ∴∠BAE=30° 在Rt△ABE中,∠BAE=30° 设BE=x,则AB=2x,AE= 在Rt△ABD中,∠BDA=30°,则∠ABD=60° ∴AD=ABtan60°= ∵S△ABE= S矩形ABCD= ∴S△ABE:S矩形ABCD= ∴ 每个三角形的面积都等于矩形ABCD面积的 的三角形有: △AFD,△ABE,△FDC,△BEC 【来源:21·世纪·教育·网】
解析:(1)利用矩形的性质易证AB∥CD,AB=CD,利用平行线的性质及垂直的定义,可证得∠ABE=∠CDF及∠AEB=∠CFD,然后利用AAS可得到△ABE≌△CDF,然后利用全等三角形的性质,可证得结论。 (2)利用全等三角形的性质,可证得BE=DF,再根据全等三角形的面积相等及等底等高的三角形的面积相等,就可证得S△AFD=S△ABE=S△FDC=S△BEC , 在Rt△ABE中,由∠BAE=30°,设BE=x,利用解直角三角形分别表示出AE、AD、AB,然后分别求出△ABE和矩形ABCD的面积,就可得到△ABE和矩形ABCD的面积之比,继而可得出结果。www-2-1-cnjy-com
15. (1)解: x2-2x-8=0,得: (x-4)(x+2)=0, ∴x-4=0, 或x+2=0, 即x1=4, 或x2=-2,? ∵点B在y轴正半轴上,∴OB=4, ∵OA=2OB,∴OA=8, ∴A的坐标为(-8,0),B的坐标为(4,0), 设直线AB的函数解析式为y=kx+b, 则, 解得:k=, b=4, ∴直线AB的函数解析式为y=x+4 ; (2)解: 如图,设F的坐标为(m, n), G‘点的坐标是(a, 0), 由旋转的特点可知,D点坐标为(-4,0),E点坐标为(0,-8), 设直线ED的函数式为y=kx+b,? 则0=-4k+b, -8=b, 解得k=-2, b=-8, ∴ y=-2x-8?, F在直线ED上,n=-2m-8 由折叠图形的特点可知,EG=EG’,FG=FG', 列关系式得: 解得m=-10, n=12,? 故F点坐标为(-10,12), (3)如图:过M作MN∥DB,交y轴于N点, 过M、N作MQ⊥BD,NP⊥BD,则四边形MNPQ为矩形, B点坐标为(0,4),D点坐标为(-4,0), 设直线BD的函数式为y=kx+b,? 则0=-4k+b, 4=b, 解得k=1, b=4, ∴ y=x+4, ∵M为OD的中点,MN∥BD,则N为OB的中点, BN=2 由于OB=OD,则∠DBO=45°,过P作PK⊥BN, 则PK=BN=1, 则P点横坐标为-1,纵坐标为-1+4=3, ∴P点坐标为(-1,3)。
解析:(1)解一元二次方程,结合OB在y轴正半轴求得B点坐标,OA在x轴负半轴,?且AO=2OB,求得A点坐标,用待定系数法求出直线AB的函数解析式即可; ? (2) 设F的坐标为(m, n), G‘点的坐标是(a, 0), 根据旋转图形的特点求得D、E点的坐标,用待定系数法求出直线DE的函数解析式,F在直线DE上,根据函数解析式则可求得m、n关系式, 根据折叠图形的特点得到 EG=EG’,FG=FG' ,据此列两个关系式,组成方程组求解即可得到m、n的值,则F点坐标可求; (3) 过M作MN∥DB,交y轴于N点,过M、N作MQ⊥BD,NP⊥BD,显然四边形MNPQ为矩形,?根据B、D点坐标用待定系数法求出直线BD的函数解析式,再由M、N是OD、OB的中点,求得M、N点坐标,过P作过P作PK⊥BN,求得PK的长度,得出P点横坐标,将其代入直线BD的函数式得到纵坐标,从而得出P点坐标。
一、单选题
1.下列结论中,矩形具有而菱形不一定具有的性质是(?? )
A.?内角和为360°???????????? ?????B.?对角线互相平分?????????? ???????C.?对角线相等?????????? ???????D.?对角线互相垂直
2.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( ??)
A.?AB=CD??????????????????????????????B.?AB=BC??????????????????????????????C.?AC⊥BD??????????????????????????????D.?AC=BD
3.对于任意的矩形,下列说法一定正确的是(?? )
A.?对角线垂直且相等 B.?四边都互相垂直 C.?四个角都相等 D.?是轴对称图形,但不是中心对称图形www.21-cn-jy.com
4.如图,矩形ABCD的对角线交于点O.若∠BAO=55°,则∠AOD等于(??? )
A.?110°????????????????????????????????????
B.?115°????????????????????????????????????
C.?120°????????????????????????????????????
D.?125°
5.如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为(??? )
A.??????????????????????????????????????????
B.?2?????????????????????????????????????????
C.??????????????????????????????????????????
D.?6
6.正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( ??) 21·cn·jy·com
A.?先变大后变小???????????????????????
B.?先变小后变大???????????????????????
C.?一直变大???????????????????????
D.?保持不变
7.将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则 的值为(?? )
A.?????????????????????????????????????????
B.?????????????????????????????????????????
C.?????????????????????????????????????????
D.?
8.如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为(??? ) 2-1-c-n-j-y
1??????????????????????????????????????????
B.????????????????????????????????????????????
C.?2??????????????????????????????????????????
D.?4
9.将三角尺按如图所示放置在一张矩形纸片上, , , ,则 的度数为(??? )
A.?130°????????????????????????????????????
B.?120°????????????????????????????????????
C.?110°????????????????????????????????????
D.?100°
10.如图,将一长方形纸片沿着虚线剪成两个全等的梯形纸片.根据图中标示长度与角度,求梯形纸片中较短的底边长度为何?(?? ) 【来源:21cnj*y.co*m】
A.?4???????????????????????????????????????????
B.?5???????????????????????????????????????????
C.?6???????????????????????????????????????????
D.?7
二、填空题
11.如图,在Rt△ABC中,∠BAC=900 , 且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为________.
12.在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是________. 21世纪教育网版权所有
三、综合题
13.如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F. 【出处:21教育名师】
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求EF的长.
14.已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)如图1,求证:AE=CF;
(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的 . 【版权所有:21教育】
15.如图,在平面直角坐标系中,O是原点,点A在x轴的负半轴上,点B在y轴的正半轴上,AO=2OB,且线段OB的长是方程x2-2x-8=0的一个根. 21教育名师原创作品
(1)求直线AB的函数解析式.
(2)将△ABD绕点O逆时针方向旋转90°得到△EDO,直线ED交线段AB 于点C,点F是直线CE上一点,分别过点E、F作x轴和y轴的平行线交于点G,将△EFG沿EF折叠,使点G的对应点落在坐标轴上,求点F的坐标.
(3)在(2)的条件下,点M是DO中点,点N、P、Q在直线BD或者y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请利用备用图画出示意图并直接写出点P的坐标;若不存在,请说明理由.
答案解析部分
一、单选题
1. C
解析:A、菱形、矩形的内角和都为360°,故不符合题意;
B、对角互相平分,菱形、矩形都具有,故不符合题意;
C、对角线相等菱形不具有,而矩形具有,故符合题意
D、对角线互相垂直,菱形具有而矩形不具有,故不符合题意,
故答案为:C.
【分析】所有的四边形的内角和都是360°;所有的平行四边形的对角线都互相平分;菱形、矩形都是四边形且都是平行四边形,故可判断A,B都不符合题意;矩形的对角线相等,但不垂直;菱形的对角线互相垂直,但不相等,故可判断C符合题意,D不符合题意。21教育网
2. D
解析:四边形的对角线互相平分,即可得出四边形为平行四边形 添加AC=BD,可根据矩形判定定理对角线相等的平行四边形是矩形,判定四边形为矩形。
故答案为:D
【分析】根据矩形的判定定理可添加条件。
3. C
解析: A.矩形的对角线相等,但不垂直,故此选项不符合题意;
B、矩形的邻边都互相垂直,对边互相平行,故此选项不符合题意;
C.矩形的四个角都相等,符合题意;
D.矩形是轴对称图形,也是中心对称图形,故此选项不符合题意.
故答案为:C. 【分析】矩形的四个角都相等且都等于90°,矩形的对边相等、对角线相等,矩形是轴对称图形也是中心对称图形,据此逐一判断即可.
4. A
解析:∵四边形ABCD是矩形,∴AC=BD,OA=OB,∠OAB=∠OBA=55°,∠AOD=∠OAB+∠OBA=55°+55°=110°. 故答案为:A
【分析】由矩形的对角线互相平分得,OA=OB,再由三角形的外角性质得到∠AOD等于∠OAB和∠OBA之和即可求解。
5. B
解析:由题意可得,大正方形的边长为 ,小正方形的边长为 ,
∴图中阴影部分的面积为: ,
故答案为:B. 【分析】根据正方形的性质可求出大正方形的边长及小正方形的边长,图中阴影部分利用平移可得一个矩形,利用矩形的面积公式计算即可.
6. D
解析:解:如图,连接DE,过点E作EH⊥CD于点H,过点D作DM⊥EC于点M
∵正方形ABCD,矩形ECFG
∴四边形AEDH是矩形
∴EH=DC=AD,FC=DM
∴S△DEC= DC·EH= EC·DM
∴DC·EH=EC·DM
∵S矩形ECFG=FC·EC=EC·DM
S正方形ABCD=AD·DC=DC·EH
∴S矩形ECFG=S正方形ABCD
∴在点E从点A移动到点B的过程中,矩形ECFG的面积保持不变。
故答案为:D
【分析】连接DE,过点E作EH⊥CD于点H,过点D作DM⊥EC于点M,易证四边形AEHD是矩形,利用正方形和矩形的性质,可证得EH=DC=AD,FC=DM,再根据同一个三角形的面积相等,可证得DC·EH=EC·DM,因此可得到在点E从点A移动到点B的过程中,矩形ECFG的面积等于正方形ABCD的面积,即可得出答案。
7. B
解析:由折叠可得,AE=OE=DE,CG=OG=DG,
∴E,G分别为AD,CD的中点,
设CD=2a,AD=2b,则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=2b,
∵∠C=90°,
∴Rt△BCG中,CG2+BC2=BG2 ,
即a2+(2b)2=(3a)2 ,
∴b2=2a2 ,
即b= a,
∴ ,
∴ 的值为 。
故答案为:B。
【分析】由折叠的性质可得,AE=OE=DE,CG=OG=DG,设CD=2a,AD=2b,则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=2b,在Rt△BCG中,利用勾股定理建立方程求解得出a,b的关系进而即可求出答案。
8. C
解析:如图,延长FH交AB于点M,
∵BE=2AE,DF=2FC,AB=AE+BE,CD=CF+DF,
∴AE:AB=1:3,CF:CD=1:3,
又∵G、H分别是AC的三等分点,
∴AG:AC=CH:AC=1:3,
∴AE:AB=AG:AC,CF:CD=CH:CA,
∴EG//BC,FH//AD,
∴△AEG∽△ABC,△CFH∽△CDA,BM:AB=CF:CD=1:3,∠EMH=∠B,
∴EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,
∵四边形ABCD是矩形,AB=3,BC=6,
∴CD=AB=3,AD=BC=6,∠B=90°,
∴AE=1,EG=2,CF=1,HF=2,BM=1,
∴EM=3-1-1=1,EG=FH,
∴EG FH,
∴四边形EHFG为平行四边形,
∴S四边形EHFG=2×1=2,
故答案为:C。
【分析】如图,延长FH交AB于点M,根据线段之间的关系可以得出AE:AB=AG:AC,CF:CD=CH:CA,根据平行线分线段成比例定理的逆用得出EG//BC,FH//AD,根据平行于三角形一边的直线,截其它两边,所截的三角形与原三角形相似得出△AEG∽△ABC,△CFH∽△CDA,根据相似三角形对应边成比例得出EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,根据矩形的性质进而即可得出EG=2,HF=2,根据一组对边平行且相等的四边形是平行四边形判断出四边形EHFG为平行四边形,进而根据平行四边形面积的计算方法即可算出答案。21*cnjy*com
9. C
解析:∵ , ,
∴ ,
又∵ , ,
∴ ,
∴ 。
故答案为:C。
【分析】根据矩形的对边平行得出AD∥BC,根据二直线平行,同旁内角互补得出∠BFE的度数,根据三角形的内角和得出∠EFG的度数,进而根据角的和差,由∠BFR+∠EFG=∠BFG算出答案。
10. C
解析:过F作FQ⊥AD于Q,
则∠FQE=90°,
∵四边形ABCD是长方形,
∴∠A=∠B=90°,AB=DC=8,AD∥BC,
∴四边形ABFQ是矩形,
∴AB=FQ=DC=8,
∵AD∥BC,
∴∠QEF=∠BFE=45°,
∴EQ=FQ=8,
∴AE=CF= ×(20-8)=6,
故答案为:C.
【分析】过F作FQ⊥AD于Q,很容易判断出四边形ABFQ是矩形,根据矩形的性质得出AB=FQ=DC=8,进而判断出△EFQ是等腰直角三角形,根据等腰直角三角形的性质得出EQ=FQ=8,从而根据线段的和差即可算出答案。2·1·c·n·j·y
二、填空题
11. (或2.4)
解析:如图,连接AD. ∵ ∠BAC=90°,且BA=3,AC=4 , ∴BC=5, ∵ DM⊥AB于点M,DN⊥AC于点N ,∠BAC=90°, ∴四边形AMCN是矩形, ∴MN=AD, 由垂线段最短可得CP⊥AB时,线段MN的值最小, 此时,△ABC的面积=, , 解得AD=即 线段MN的最小值为 : 故答案为: 【分析】首先根据UGG多了算出BC的长,然后判断出四边形AMCN是矩形,根据矩形的对角线相等得出MN=AD,由垂线段最短可得CP⊥AB时,线段MN的值最小,然后滚局三角形的面积法即可算出AD的长,从而得出答案。21·世纪*教育网
12. ①②③
解析:①如图,∵四边形ABCD是矩形,连接AC,BD交于O,
过点O直线MP和QN,分别交AB,BC,CD,AD于M,N,P,Q,
则四边形MNPQ是平行四边形,
故当MQ∥PN,PQ∥MN,四边形MNPQ是平行四边形,
故存在无数个四边形MNPQ是平行四边形;故正确;
②如图,当PM=QN时,四边形MNPQ是菱形,故存在无数个四边形MNPQ是矩形;故正确;
③如图,当PM⊥QN时,存在无数个四边形MNPQ是菱形;故正确;
④当四边形MNPQ是正方形时,MQ=PQ,
则△AMQ≌△DQP,
∴AM=QD,AQ=PD,
∵PD=BM,
∴AB=AD,
∴四边形ABCD是正方形与任意矩形ABCD矛盾,故错误;
故答案为:①②③.
【分析】分别根据矩形,平行四边形,菱形的判定定理以及性质得到答案即可。
三、综合题
13. (1)证明:∵四边形ABCD是矩形
∴AB∥CD
∴∠DFO=∠BEO,
又因为∠DOF=∠BOE,OD=OB
∴△DOF≌△BOE∴DF=BE
又因为DF∥BE,
∴四边形BEDF是平行四边形 (2)解:∵DE=DF,四边形BEDF是平行四边形
∴ BEDF是菱形∴DE=BE,EF⊥BD,OE=OF
设AE=x,则DE=BE=8-x
在Rt△ADE中,根据勾股定理,有AE2+AD2=DE2
∴x2+62=(8-x)2解之得:x=
∴DE=8- =
在Rt△ABD中,根据勾股定理,有AB2+AD2=BD2
∴BD= ∴OD= BD=5,
在Rt△DOE中,根据勾股定理,有DE2-OD2=OE2 ,
∴OE=
∴EF=2OE=
解析:(1)抓住题给条件 点O是对角线BD的中点,证明三角形全等,得对应边相等。再利用平行四边形判定定理,一组对边平行且相等是平行四边形。 (2)因为邻边相等的平行四边形是菱形,由菱形的性质知,四边都相等,在Rt△ADE中,设AE=x, 利用勾股定理列关系式解出x. x值解出,后面就容易了,根据菱形性质对角线互相垂直平分,用勾股定理即可求解。21cnjy.com
14. (1)证明: ∵四边形ABCD是矩形 ∴AB∥CD,AB=CD ∴∠ABE=∠CDF ∵AE⊥BD,CE⊥BD ∴∠AEB=∠CFD=90° 在△ABE和△CDF中 ∴△ABE≌△CDF(AAS) ∴AE=CF (2)解: ∵△ABE≌△CDF ∴BE=DF ∴S△AFD=S△ABE=S△FDC=S△BEC ∵ ∠ADB=30° ∴∠BAE=30° 在Rt△ABE中,∠BAE=30° 设BE=x,则AB=2x,AE= 在Rt△ABD中,∠BDA=30°,则∠ABD=60° ∴AD=ABtan60°= ∵S△ABE= S矩形ABCD= ∴S△ABE:S矩形ABCD= ∴ 每个三角形的面积都等于矩形ABCD面积的 的三角形有: △AFD,△ABE,△FDC,△BEC 【来源:21·世纪·教育·网】
解析:(1)利用矩形的性质易证AB∥CD,AB=CD,利用平行线的性质及垂直的定义,可证得∠ABE=∠CDF及∠AEB=∠CFD,然后利用AAS可得到△ABE≌△CDF,然后利用全等三角形的性质,可证得结论。 (2)利用全等三角形的性质,可证得BE=DF,再根据全等三角形的面积相等及等底等高的三角形的面积相等,就可证得S△AFD=S△ABE=S△FDC=S△BEC , 在Rt△ABE中,由∠BAE=30°,设BE=x,利用解直角三角形分别表示出AE、AD、AB,然后分别求出△ABE和矩形ABCD的面积,就可得到△ABE和矩形ABCD的面积之比,继而可得出结果。www-2-1-cnjy-com
15. (1)解: x2-2x-8=0,得: (x-4)(x+2)=0, ∴x-4=0, 或x+2=0, 即x1=4, 或x2=-2,? ∵点B在y轴正半轴上,∴OB=4, ∵OA=2OB,∴OA=8, ∴A的坐标为(-8,0),B的坐标为(4,0), 设直线AB的函数解析式为y=kx+b, 则, 解得:k=, b=4, ∴直线AB的函数解析式为y=x+4 ; (2)解: 如图,设F的坐标为(m, n), G‘点的坐标是(a, 0), 由旋转的特点可知,D点坐标为(-4,0),E点坐标为(0,-8), 设直线ED的函数式为y=kx+b,? 则0=-4k+b, -8=b, 解得k=-2, b=-8, ∴ y=-2x-8?, F在直线ED上,n=-2m-8 由折叠图形的特点可知,EG=EG’,FG=FG', 列关系式得: 解得m=-10, n=12,? 故F点坐标为(-10,12), (3)如图:过M作MN∥DB,交y轴于N点, 过M、N作MQ⊥BD,NP⊥BD,则四边形MNPQ为矩形, B点坐标为(0,4),D点坐标为(-4,0), 设直线BD的函数式为y=kx+b,? 则0=-4k+b, 4=b, 解得k=1, b=4, ∴ y=x+4, ∵M为OD的中点,MN∥BD,则N为OB的中点, BN=2 由于OB=OD,则∠DBO=45°,过P作PK⊥BN, 则PK=BN=1, 则P点横坐标为-1,纵坐标为-1+4=3, ∴P点坐标为(-1,3)。
解析:(1)解一元二次方程,结合OB在y轴正半轴求得B点坐标,OA在x轴负半轴,?且AO=2OB,求得A点坐标,用待定系数法求出直线AB的函数解析式即可; ? (2) 设F的坐标为(m, n), G‘点的坐标是(a, 0), 根据旋转图形的特点求得D、E点的坐标,用待定系数法求出直线DE的函数解析式,F在直线DE上,根据函数解析式则可求得m、n关系式, 根据折叠图形的特点得到 EG=EG’,FG=FG' ,据此列两个关系式,组成方程组求解即可得到m、n的值,则F点坐标可求; (3) 过M作MN∥DB,交y轴于N点,过M、N作MQ⊥BD,NP⊥BD,显然四边形MNPQ为矩形,?根据B、D点坐标用待定系数法求出直线BD的函数解析式,再由M、N是OD、OB的中点,求得M、N点坐标,过P作过P作PK⊥BN,求得PK的长度,得出P点横坐标,将其代入直线BD的函数式得到纵坐标,从而得出P点坐标。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
