1.1 菱形的性质与判定 同步练习(解析版)
文档属性
| 名称 | 1.1 菱形的性质与判定 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 00:00:00 | ||
图片预览



文档简介
初中数学北师大版九年级上学期 第一章 1.1 菱形的性质与判定
一、单选题
1.菱形不具备的性质是(?? )
A.?是轴对称图形???????????????B.?是中心对称图形???????????????C.?对角线互相垂直???????????????D.?对角线一定相等
2.下列说法正确的是(?? ?)
A.?一组对边平行,另一组对边相等的四边形是平行四边形 B.?对角线相等的平行四边形是菱形 C.?三个角都是直角的四边形是矩形 D.?一组邻边相等的平行四边形是正方形www.21-cn-jy.com
3.在数学课拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长是1,且一个内角是60°的小菱形拼成的图形,P是其中4个小菱形的公共顶点,小新在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是(??? ) 【来源:21·世纪·教育·网】
A.?2 ???????????????????????????????????B.?3 ???????????????????????????????????
C.????????????????????????????????????D.?
4.在正方形ABCD中,E、F是对角线AC上两点连接BE、BF、DE、DF,则A添加下列哪一个条件可以判定四边形BEDF是菱形( ??) 21·世纪*教育网
A.?∠1=∠2???????????????????????? ?????B.?BE=DF?????????????????????????????
C.?∠EDF=60°?????????????????????????????D.?AB=AF
5.如图,在四边形 中, , 是对角线, 分别是 的中点,连接 ,则四边形 的形状是( ??) 2-1-c-n-j-y
A.?平行四边形????????????????????????????????
B.?矩形????????????????????????????????
C.?菱形????????????????????????????????
D.?正方形
6.一个菱形的边长为 ,面积为 ,则该菱形的两条对角线的长度之和为( ??)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
7.如图,正方形ABCD的边长为3,点EF在正方形ABCD内若四边形AECF恰是菱形连结FB,DE,且AF2-FB2=3,则菱形AECF的边长为(??? ). 【出处:21教育名师】
A.?????????????????????????????????????????
B.?????????????????????????????????????????
C.?2????????????????????????????????????????
D.?
8.如图,在菱形 中,E,F分别是 的中点,若∠B=50°,则∠AFE的度数为( ??)
A.?50°??????????????????????????????????????
B.?60°???????????????????????????????????????
C.?65°???????????????????????????????????????
D.?70°
9.如图,在平面直角坐标系xOy中,已知点A( ,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是(??? )
A.?向左平移1个单位,再向下平移1个单位??????????????
B.?向左平移(2 -1个单位,再向上平移1个单位 C.?向右平移 个单位,再向上平移1个单位?????????
D.?向右平移1个单位,再向上平移1个单位
二、填空题
10.如图,将菱形纸片ABCD折叠,使点C,D的对应点C',D'都落在直线AB上,折痕为EF,若EF=6.AC'=8,则阴影部分(四边形ED'BF)的面积为________?。
11.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H,已知BO=4,S菱形ABCD=24,则AH=________?.
12.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是________.
13.如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是________.
三、作图题
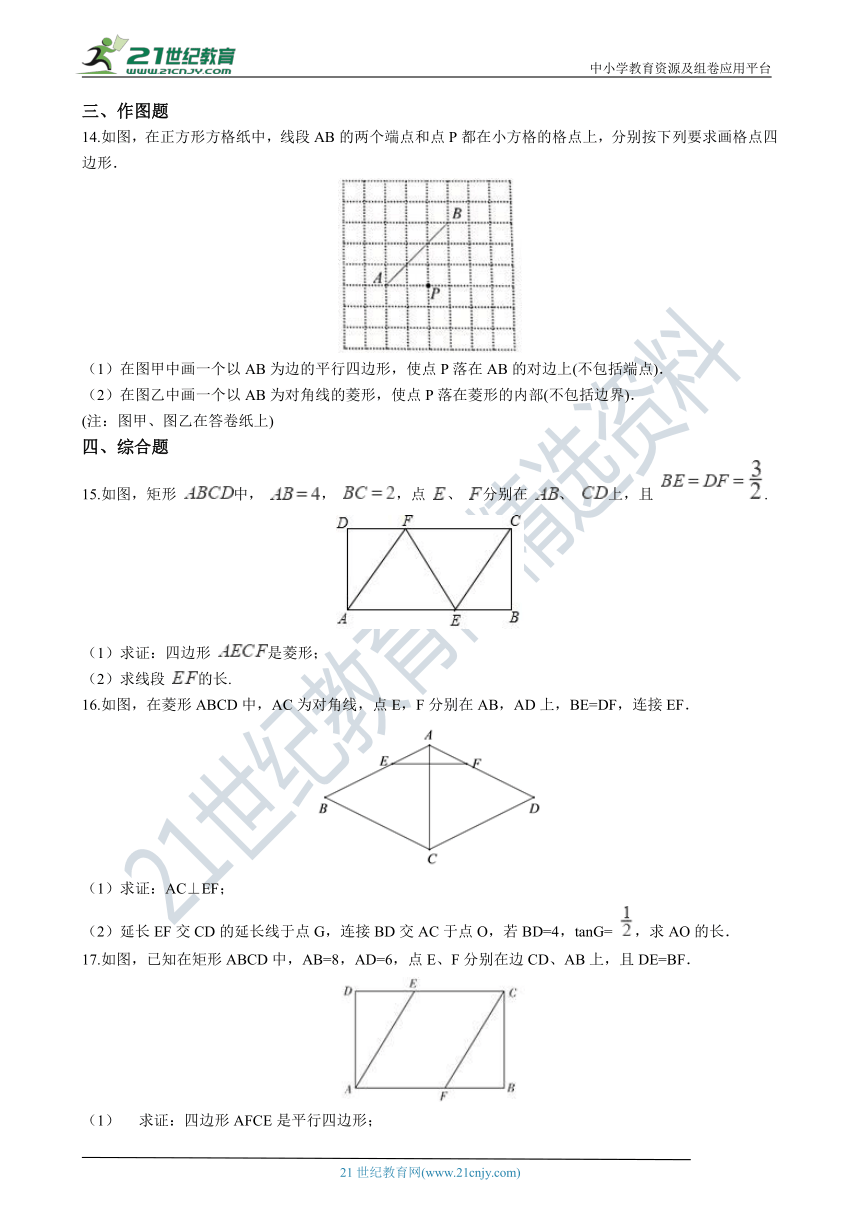
14.如图,在正方形方格纸中,线段AB的两个端点和点P都在小方格的格点上,分别按下列要求画格点四边形. www-2-1-cnjy-com
(1)在图甲中画一个以AB为边的平行四边形,使点P落在AB的对边上(不包括端点).
(2)在图乙中画一个以AB为对角线的菱形,使点P落在菱形的内部(不包括边界).
(注:图甲、图乙在答卷纸上)
四、综合题
15.如图,矩形 中, , ,点 、 分别在 、 上,且 .
(1)求证:四边形 是菱形;
(2)求线段 的长.
16.如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连接EF.
(1)求证:AC⊥EF;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O,若BD=4,tanG= ,求AO的长.
17.如图,已知在矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上,且DE=BF.
(1)? 求证:四边形AFCE是平行四边形;
(2)若□AFCE是菱形,求菱形AFCE的周长.
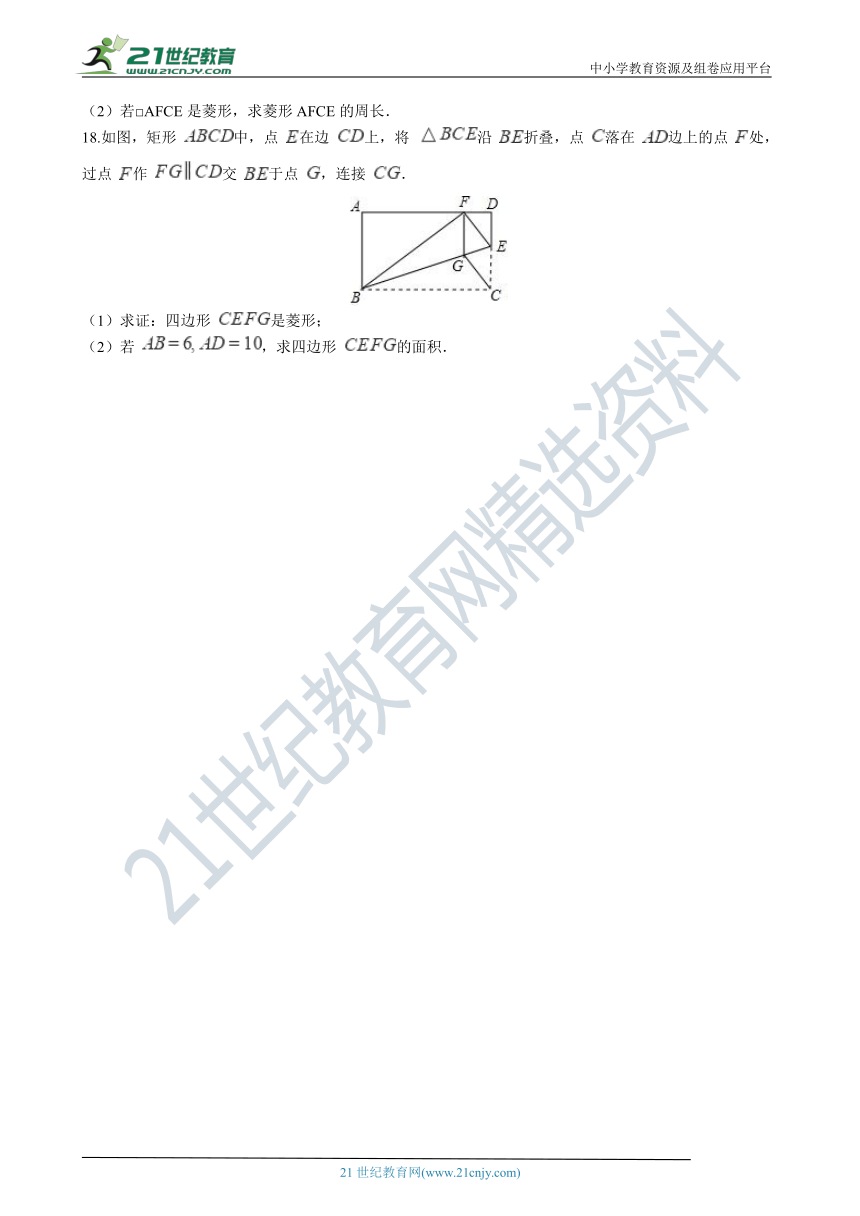
18.如图,矩形 中,点 在边 上,将 沿 折叠,点 落在 边上的点 处,过点 作 交 于点 ,连接 . 21教育网
(1)求证:四边形 是菱形;
(2)若 ,求四边形 的面积.
答案解析部分
一、单选题
1. D
解析:A、是轴对称图形,故正确,但不符合题意;
B、是中心对称图形,故正确,但不符合题意;
C、对角线互相垂直,故正确,但不符合题意;
D、对角线不一定相等,故不正确,符合题意。
故答案为:D。
【分析】根据菱形的性质即可一一判断得出答案。
2. C
解析:A、 一组对边平行且相等,或两组对边分别相等的的四边形是平行四边形?, 不符合题意; B、 对角线相等的平行四边形是矩形,不符合题意; C、三个角都是直角的四边形是矩形,符合题意; D、 一组邻边相等的平行四边形是菱形, 不符合题意. 故答案为:C 【分析】分别根据平行四边形、矩形、菱形、正方形的判定定理分析即可判断。21教育名师原创作品
3. D
解析:如图据题意,剪痕是连接两个菱形的对角线的交点的直线, 作OH⊥AC,PG⊥BC,OM⊥PG, ∵在小菱形中,∠OAC=30°,∠AOC=90°, ∴OC=, 又∵∠OCH=60°, , 同理PG=?, ?, 由图可得:?, , ∵菱形是中心对称图形, ∴LO=JO, KP=JP, ∴LO+KP=JO+JP, ∴剪痕:?. 故答案为:D 【分析】先根据题意找出折痕,因为折痕同时平分两个菱形的面积,则折痕是两个菱形对角线的交点连线。作垂线,构造直角三角形,利用勾股定理求出有关线段的长,现知OP的长,由于菱形是中心对称图形,所以折痕是OP长的2倍,从而求出折痕的长。21*cnjy*com
4. B
解析:可添加条件BE=BF, ∵AB=AD, ∠ DAE= ∠ BAE,AE=AE ∴A△ADEQ≌△ABE(SAS) 所以ED=EB,DF=EF,EB=FB, ∴四边形BEDF是菱形. 【来源:21cnj*y.co*m】
故答案为:B.
【分析】根据三角形全等的判定定理判定全等,利用性质和添加的条件可证得菱形。
5. C
解析:∵ 分别是 的中点,
∴在 中, 为 的中位线,所以 且 ;同理 且 ,同理可得 ,
则 且 ,
∴四边形 为平行四边形,又 ,所以 ,
∴四边形 为菱形.
故答案为:C. 【分析】根据三角形中位线定理可得且 , 且 ?,?,从而可得EH∥FG且EH=FG,利用一组对边平行且相等可证四边形EFGH为平行四边形,由AB=CD,即得EF=EH,利用一组邻边相等的平行四边形是菱形即证.
6. C
解析:如图所示:
四边形 是菱形,
, , ,
面积为 ,
? ①
菱形的边长为 ,
②,
由①②两式可得: ,
,
,
即该菱形的两条对角线的长度之和为 ,
故答案为:C. 【分析】根据菱形的面积=对角线乘积的一半=底×高,可得2OD·OA=28.利用菱形的性质及勾股定理可得OD2+OA2=36,从而求出OD+OA的长,继而求出菱形的两条对角线的长度之和.21*cnjy*com
7. A
解析:如图,连接AC、EF,
则AC垂直平分BD,也垂直平分EF, ∵AB=3,AC= 则OA=OB=, AF2=OA2+OF2=OA2+(OA-FB)2 , AF2=+(-FB)2 , AF2=+-3FB+FB2 , AF2-FB2=9-?3FB=3, 3FB=6, 则FB=, 故答案为:A. 【分析】连接AC、EF,利用勾股定理先求出AC,则得OA和OB的长度,再根据已知条件 AF2-FB2=3 列式,求解FB即可。【版权所有:21教育】
8. C
解析:∵四边形ABCD是菱形, ∴AB=BC, ∵∠B=50°, ∴∠BCA=, ∵E、F分别是AB、AC的中点, ∴EF是△ABC的中位线, ∴EF∥BC, ∴∠AFE=∠ACB=65°. 故答案为:C 【分析】因为EF是中位线,根据两直线平行同位角相等,把∠AEF转化为∠ACB, 由四边形ABCD是菱形,得到AB=BC,再由三角形内角和定理得到∠ACB=65°,即可求出∠AFE。
9. D
解析:过B作射线BD∥OA,在射线BC上截取BC=OA,则四边形OACB是平行四边形, 过B作BH⊥x轴于H, ∵B(1,1), ∴BH=OH=1 ∴OB= ∵A(, 0), ∴OA= ∴OA=OB, ∴四边形OACB是菱形 ∴点C的横坐标为OA+OH=+1 ∴C(1+, 1) ∵A(, 0), ∴点A平移到点C,是向右平移1个单位,再向上平移1个单位而得到。 故答案为:D
【分析】过B作射线BC∥OA,在BC上截取BC=OA,则四边形OACB是平行四边形,过B作BH⊥x轴于H,在Rt△OBH中,利用勾股定理可求出OB的长,再根据点A的坐标可得到OA的长,就可证得OA=OB,可知四边形OACB是菱形,利用菱形的性质,可得到点C的坐标,然后根据点A、C的坐标变化,可得到点A向左或向右平移的距离,及向上或向下平移的距离。
二、填空题
10. 10
解析:如图,过E作EH⊥AC’,? 由对称图形的特征可知: EF=AB=D'C', ∴AD'+D'B=D'B+BC', ∴AD'=BC’, ∵AB+BC‘=AC'=8, ∴BC'=8-6=2=AD', ∴BD'=AB-AD'=6-2=4, 又∵EA=ED', ∴, , 故答案为: 10?, 【分析】根据对称图形的特点,算出BC和AD’的长,则D'B的长可求,然后过E作EH垂直AB, 由勾股定理求出EH的长,将所求线段代入梯形面积公式即可求出阴影部分的面积。
11.
解析:∵四边形ABCD是菱形 ∴BD=2OB=2×4=8, ∵S菱形ABCD= 解之:AC=6 ∴OC=AC=×6=3 在Rt△OBC中 BC= ∵ S菱形ABCD=24, AH⊥BC ∴BC·AH=24=5AH 解之:AH= 故答案为: 【分析】利用菱形的性质,可求出BD的长,再根据菱形的面积等于两对角线之积的一半,就可求出AC的长,从而可得OC的长,利用勾股定理求出BC,然后利用菱形的面积等于底乘以高,就可求出AH的长。
12. ﹣1
解析:连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC= ∠BAD=30°,OA=OC,AC⊥BD,
∴OB= AB=1,
∴OA= OB= ,
∴AC=2 ,
由旋转的性质得:AE=AB=2,∠EAG=∠BAD=60°,
∴CE=AC﹣AE=2 ﹣2,
∵四边形AEFG是菱形,
∴EF∥AG,
∴∠CEP=∠EAG=60°,
∴∠CEP+∠ACD=90°,
∴∠CPE=90°,
∴PE= CE= ﹣1,PC= PE=3﹣ ,
∴DP=CD﹣PC=2﹣(3﹣ )= ﹣1。
故答案为 ﹣1。
【分析】连接BD交AC于O,如图所示:根据菱形的性质得出CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC= ∠BAD=30°,OA=OC,AC⊥BD,根据含30°角的直角三角形的边之间的关系得出OB、OA的长,进而得出AC的长,由旋转的性质得:AE=AB=2,∠EAG=∠BAD=60°,根据线段的和差得出CE的长,根据二直线平行,同位角相等得出∠CEP=∠EAG=60°,进而根据三角形的内角和得出∠CPE=90°,根据含30°角的直角三角形的边之间的关系得出PE,PC的长,最后根据DP=CD﹣PC算出答案。
13.
解析:如图,连接 交 于点 ,
∵四边形 为正方形,
∴ , ,
∵ ,
∴ ,即 ,
∴四边形 为平行四边形,且 ,
∴四边形 为菱形,
∴ ,
∵ , ,
由勾股定理得: ,
∴四边形 的周长 ,
故答案为: . 【分析】根据正方形的对角线相等且互相垂直平分得到=, 且, 则可得OE=OF,由对角线互相垂直平分的四边形为菱形可得四边形 为菱形,在Rt△DOE中根据勾股定理可得DE的长,则四边形 的周长=4DE。21世纪教育网版权所有
三、作图题
14. (1)解:如下图
(2)解:如下图
解析:(1)根据一组对边平行且相等是平行四边形,过P作AB的平行线,使其作为平行四边形的一边,并且使这条边等于AB,端点在格点上即可。方案不唯一。 (2)根据四条边相等的四边形是菱形,由三角形全等的性质构造菱形的四条边,且使P点在菱形的内部即可。方案不唯一。
四、综合题
15. (1)证明:∵在矩形 中, , ,
∴ , , , ,
∵ ,
∴ ,
∴ ,
∴ ,
∴四边形 是菱形 (2)解:过 作 于 ,
则四边形 是矩形,
∴ , ,
∴ ,
∴
解析:(1)根据矩形的性质得出 , , , , 根据线段的和差得出 , 根据勾股定理得出AF=CE=,故 ,根据四边相等的四边形是菱形得出结论: 四边形 是菱形 ; (2) 过 作 于 , 很容易得知 四边形 是矩形 根据矩形的性质得出 , ,进而利用勾股定理即可算出EF的长。21cnjy.com
16. (1)证明:∵四边形ABCD为菱形? ∴AB=AD,AC平分∠BAD
∵BE=DF, ∴ ? , ∴AE=AF
∴△AEF是等腰三角形, ∵AC平分∠BAD, ∴AC⊥EF (2)解:如图2所示:
∵四边形ABCD为菱形,∴CG∥AB,BO= BD=2,∵EF∥BD
∴四边形EBDG为平行四边形,∴∠G=∠ABD,∴tan∠ABD=tan∠G=
∴tan∠ABD= ,∴AO=1
解析:(1)根据菱形的性质,即可判断三角形AEF为等腰三角形,即可求出答案。 (2)根据菱形的性质,证明四边形EBDG为平行四边形,得到答案即可。
17. (1)证明:在矩形ABCD中,
∴AB//CD,AB=CD,
∵DE=BF,
∴CE=AF,且CE//AF,
∴四边形AFCE是平行四边形. (2)解:∵平行四边形AFCE是菱形,
∴AE=CE,
设AE=CE=x,
∵AB=CD=8,AD=6,∴DE=8-x,
在矩形ABCD中,∠D=90°,
∴AD2+DE2=AE2 ,
(8-x)2+62=x2,
解得 .
∴菱形的周长为25.
解析:(1)矩形的对边互相平行且相等,由DE=BF,等量代换得EC=AF,根据一组对边平行且相等求得 四边形AFCE是平行四边形。 (2)设菱形的边长为x,把DE、AE用含x的代数式表示,在Rt△ADE中,用勾股定理列式,求出x. 则菱形的周长可求。21·cn·jy·com
18. (1)证明:由题意可得,
,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴四边形 是平行四边形,
又∵
∴四边形 是菱形 (2)解:∵矩形 中, ,
∴ ,
∴ ,
∴ ,
设 ,则 ,
∵ ,
∴ ,
解得, ,
∴ ,
∴四边形 的面积是:
解析:(1)根据折叠的性质,可得∠BEC=∠BEF,EF=CE.根据两直线平行,内错角相等,可得∠FGE=∠BEF,即得∠FGE=∠FEG,由等角对等边,可得FG=EF,即得FG=EC,利用一组对边平行且相等的四边形是平行四边形,可证四边形CEFG是平行四边形,由CE=EF,即证四边形CEFG是菱形。 (2)根据矩形的矩形的性质及折叠的性质,可得∠BAF=90°,AD=BC=BF=10,由勾股定理可求AF=8,从而可得DF=2,设? ? , 则? ?,在Rt△DEF中,可得22+(6-x)2=x2,求出x的值,即得CE的长,利用平行四边形的面积公式计算即可.2·1·c·n·j·y
一、单选题
1.菱形不具备的性质是(?? )
A.?是轴对称图形???????????????B.?是中心对称图形???????????????C.?对角线互相垂直???????????????D.?对角线一定相等
2.下列说法正确的是(?? ?)
A.?一组对边平行,另一组对边相等的四边形是平行四边形 B.?对角线相等的平行四边形是菱形 C.?三个角都是直角的四边形是矩形 D.?一组邻边相等的平行四边形是正方形www.21-cn-jy.com
3.在数学课拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长是1,且一个内角是60°的小菱形拼成的图形,P是其中4个小菱形的公共顶点,小新在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是(??? ) 【来源:21·世纪·教育·网】
A.?2 ???????????????????????????????????B.?3 ???????????????????????????????????
C.????????????????????????????????????D.?
4.在正方形ABCD中,E、F是对角线AC上两点连接BE、BF、DE、DF,则A添加下列哪一个条件可以判定四边形BEDF是菱形( ??) 21·世纪*教育网
A.?∠1=∠2???????????????????????? ?????B.?BE=DF?????????????????????????????
C.?∠EDF=60°?????????????????????????????D.?AB=AF
5.如图,在四边形 中, , 是对角线, 分别是 的中点,连接 ,则四边形 的形状是( ??) 2-1-c-n-j-y
A.?平行四边形????????????????????????????????
B.?矩形????????????????????????????????
C.?菱形????????????????????????????????
D.?正方形
6.一个菱形的边长为 ,面积为 ,则该菱形的两条对角线的长度之和为( ??)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
7.如图,正方形ABCD的边长为3,点EF在正方形ABCD内若四边形AECF恰是菱形连结FB,DE,且AF2-FB2=3,则菱形AECF的边长为(??? ). 【出处:21教育名师】
A.?????????????????????????????????????????
B.?????????????????????????????????????????
C.?2????????????????????????????????????????
D.?
8.如图,在菱形 中,E,F分别是 的中点,若∠B=50°,则∠AFE的度数为( ??)
A.?50°??????????????????????????????????????
B.?60°???????????????????????????????????????
C.?65°???????????????????????????????????????
D.?70°
9.如图,在平面直角坐标系xOy中,已知点A( ,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是(??? )
A.?向左平移1个单位,再向下平移1个单位??????????????
B.?向左平移(2 -1个单位,再向上平移1个单位 C.?向右平移 个单位,再向上平移1个单位?????????
D.?向右平移1个单位,再向上平移1个单位
二、填空题
10.如图,将菱形纸片ABCD折叠,使点C,D的对应点C',D'都落在直线AB上,折痕为EF,若EF=6.AC'=8,则阴影部分(四边形ED'BF)的面积为________?。
11.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H,已知BO=4,S菱形ABCD=24,则AH=________?.
12.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是________.
13.如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是________.
三、作图题
14.如图,在正方形方格纸中,线段AB的两个端点和点P都在小方格的格点上,分别按下列要求画格点四边形. www-2-1-cnjy-com
(1)在图甲中画一个以AB为边的平行四边形,使点P落在AB的对边上(不包括端点).
(2)在图乙中画一个以AB为对角线的菱形,使点P落在菱形的内部(不包括边界).
(注:图甲、图乙在答卷纸上)
四、综合题
15.如图,矩形 中, , ,点 、 分别在 、 上,且 .
(1)求证:四边形 是菱形;
(2)求线段 的长.
16.如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连接EF.
(1)求证:AC⊥EF;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O,若BD=4,tanG= ,求AO的长.
17.如图,已知在矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上,且DE=BF.
(1)? 求证:四边形AFCE是平行四边形;
(2)若□AFCE是菱形,求菱形AFCE的周长.
18.如图,矩形 中,点 在边 上,将 沿 折叠,点 落在 边上的点 处,过点 作 交 于点 ,连接 . 21教育网
(1)求证:四边形 是菱形;
(2)若 ,求四边形 的面积.
答案解析部分
一、单选题
1. D
解析:A、是轴对称图形,故正确,但不符合题意;
B、是中心对称图形,故正确,但不符合题意;
C、对角线互相垂直,故正确,但不符合题意;
D、对角线不一定相等,故不正确,符合题意。
故答案为:D。
【分析】根据菱形的性质即可一一判断得出答案。
2. C
解析:A、 一组对边平行且相等,或两组对边分别相等的的四边形是平行四边形?, 不符合题意; B、 对角线相等的平行四边形是矩形,不符合题意; C、三个角都是直角的四边形是矩形,符合题意; D、 一组邻边相等的平行四边形是菱形, 不符合题意. 故答案为:C 【分析】分别根据平行四边形、矩形、菱形、正方形的判定定理分析即可判断。21教育名师原创作品
3. D
解析:如图据题意,剪痕是连接两个菱形的对角线的交点的直线, 作OH⊥AC,PG⊥BC,OM⊥PG, ∵在小菱形中,∠OAC=30°,∠AOC=90°, ∴OC=, 又∵∠OCH=60°, , 同理PG=?, ?, 由图可得:?, , ∵菱形是中心对称图形, ∴LO=JO, KP=JP, ∴LO+KP=JO+JP, ∴剪痕:?. 故答案为:D 【分析】先根据题意找出折痕,因为折痕同时平分两个菱形的面积,则折痕是两个菱形对角线的交点连线。作垂线,构造直角三角形,利用勾股定理求出有关线段的长,现知OP的长,由于菱形是中心对称图形,所以折痕是OP长的2倍,从而求出折痕的长。21*cnjy*com
4. B
解析:可添加条件BE=BF, ∵AB=AD, ∠ DAE= ∠ BAE,AE=AE ∴A△ADEQ≌△ABE(SAS) 所以ED=EB,DF=EF,EB=FB, ∴四边形BEDF是菱形. 【来源:21cnj*y.co*m】
故答案为:B.
【分析】根据三角形全等的判定定理判定全等,利用性质和添加的条件可证得菱形。
5. C
解析:∵ 分别是 的中点,
∴在 中, 为 的中位线,所以 且 ;同理 且 ,同理可得 ,
则 且 ,
∴四边形 为平行四边形,又 ,所以 ,
∴四边形 为菱形.
故答案为:C. 【分析】根据三角形中位线定理可得且 , 且 ?,?,从而可得EH∥FG且EH=FG,利用一组对边平行且相等可证四边形EFGH为平行四边形,由AB=CD,即得EF=EH,利用一组邻边相等的平行四边形是菱形即证.
6. C
解析:如图所示:
四边形 是菱形,
, , ,
面积为 ,
? ①
菱形的边长为 ,
②,
由①②两式可得: ,
,
,
即该菱形的两条对角线的长度之和为 ,
故答案为:C. 【分析】根据菱形的面积=对角线乘积的一半=底×高,可得2OD·OA=28.利用菱形的性质及勾股定理可得OD2+OA2=36,从而求出OD+OA的长,继而求出菱形的两条对角线的长度之和.21*cnjy*com
7. A
解析:如图,连接AC、EF,
则AC垂直平分BD,也垂直平分EF, ∵AB=3,AC= 则OA=OB=, AF2=OA2+OF2=OA2+(OA-FB)2 , AF2=+(-FB)2 , AF2=+-3FB+FB2 , AF2-FB2=9-?3FB=3, 3FB=6, 则FB=, 故答案为:A. 【分析】连接AC、EF,利用勾股定理先求出AC,则得OA和OB的长度,再根据已知条件 AF2-FB2=3 列式,求解FB即可。【版权所有:21教育】
8. C
解析:∵四边形ABCD是菱形, ∴AB=BC, ∵∠B=50°, ∴∠BCA=, ∵E、F分别是AB、AC的中点, ∴EF是△ABC的中位线, ∴EF∥BC, ∴∠AFE=∠ACB=65°. 故答案为:C 【分析】因为EF是中位线,根据两直线平行同位角相等,把∠AEF转化为∠ACB, 由四边形ABCD是菱形,得到AB=BC,再由三角形内角和定理得到∠ACB=65°,即可求出∠AFE。
9. D
解析:过B作射线BD∥OA,在射线BC上截取BC=OA,则四边形OACB是平行四边形, 过B作BH⊥x轴于H, ∵B(1,1), ∴BH=OH=1 ∴OB= ∵A(, 0), ∴OA= ∴OA=OB, ∴四边形OACB是菱形 ∴点C的横坐标为OA+OH=+1 ∴C(1+, 1) ∵A(, 0), ∴点A平移到点C,是向右平移1个单位,再向上平移1个单位而得到。 故答案为:D
【分析】过B作射线BC∥OA,在BC上截取BC=OA,则四边形OACB是平行四边形,过B作BH⊥x轴于H,在Rt△OBH中,利用勾股定理可求出OB的长,再根据点A的坐标可得到OA的长,就可证得OA=OB,可知四边形OACB是菱形,利用菱形的性质,可得到点C的坐标,然后根据点A、C的坐标变化,可得到点A向左或向右平移的距离,及向上或向下平移的距离。
二、填空题
10. 10
解析:如图,过E作EH⊥AC’,? 由对称图形的特征可知: EF=AB=D'C', ∴AD'+D'B=D'B+BC', ∴AD'=BC’, ∵AB+BC‘=AC'=8, ∴BC'=8-6=2=AD', ∴BD'=AB-AD'=6-2=4, 又∵EA=ED', ∴, , 故答案为: 10?, 【分析】根据对称图形的特点,算出BC和AD’的长,则D'B的长可求,然后过E作EH垂直AB, 由勾股定理求出EH的长,将所求线段代入梯形面积公式即可求出阴影部分的面积。
11.
解析:∵四边形ABCD是菱形 ∴BD=2OB=2×4=8, ∵S菱形ABCD= 解之:AC=6 ∴OC=AC=×6=3 在Rt△OBC中 BC= ∵ S菱形ABCD=24, AH⊥BC ∴BC·AH=24=5AH 解之:AH= 故答案为: 【分析】利用菱形的性质,可求出BD的长,再根据菱形的面积等于两对角线之积的一半,就可求出AC的长,从而可得OC的长,利用勾股定理求出BC,然后利用菱形的面积等于底乘以高,就可求出AH的长。
12. ﹣1
解析:连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC= ∠BAD=30°,OA=OC,AC⊥BD,
∴OB= AB=1,
∴OA= OB= ,
∴AC=2 ,
由旋转的性质得:AE=AB=2,∠EAG=∠BAD=60°,
∴CE=AC﹣AE=2 ﹣2,
∵四边形AEFG是菱形,
∴EF∥AG,
∴∠CEP=∠EAG=60°,
∴∠CEP+∠ACD=90°,
∴∠CPE=90°,
∴PE= CE= ﹣1,PC= PE=3﹣ ,
∴DP=CD﹣PC=2﹣(3﹣ )= ﹣1。
故答案为 ﹣1。
【分析】连接BD交AC于O,如图所示:根据菱形的性质得出CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC= ∠BAD=30°,OA=OC,AC⊥BD,根据含30°角的直角三角形的边之间的关系得出OB、OA的长,进而得出AC的长,由旋转的性质得:AE=AB=2,∠EAG=∠BAD=60°,根据线段的和差得出CE的长,根据二直线平行,同位角相等得出∠CEP=∠EAG=60°,进而根据三角形的内角和得出∠CPE=90°,根据含30°角的直角三角形的边之间的关系得出PE,PC的长,最后根据DP=CD﹣PC算出答案。
13.
解析:如图,连接 交 于点 ,
∵四边形 为正方形,
∴ , ,
∵ ,
∴ ,即 ,
∴四边形 为平行四边形,且 ,
∴四边形 为菱形,
∴ ,
∵ , ,
由勾股定理得: ,
∴四边形 的周长 ,
故答案为: . 【分析】根据正方形的对角线相等且互相垂直平分得到=, 且, 则可得OE=OF,由对角线互相垂直平分的四边形为菱形可得四边形 为菱形,在Rt△DOE中根据勾股定理可得DE的长,则四边形 的周长=4DE。21世纪教育网版权所有
三、作图题
14. (1)解:如下图
(2)解:如下图
解析:(1)根据一组对边平行且相等是平行四边形,过P作AB的平行线,使其作为平行四边形的一边,并且使这条边等于AB,端点在格点上即可。方案不唯一。 (2)根据四条边相等的四边形是菱形,由三角形全等的性质构造菱形的四条边,且使P点在菱形的内部即可。方案不唯一。
四、综合题
15. (1)证明:∵在矩形 中, , ,
∴ , , , ,
∵ ,
∴ ,
∴ ,
∴ ,
∴四边形 是菱形 (2)解:过 作 于 ,
则四边形 是矩形,
∴ , ,
∴ ,
∴
解析:(1)根据矩形的性质得出 , , , , 根据线段的和差得出 , 根据勾股定理得出AF=CE=,故 ,根据四边相等的四边形是菱形得出结论: 四边形 是菱形 ; (2) 过 作 于 , 很容易得知 四边形 是矩形 根据矩形的性质得出 , ,进而利用勾股定理即可算出EF的长。21cnjy.com
16. (1)证明:∵四边形ABCD为菱形? ∴AB=AD,AC平分∠BAD
∵BE=DF, ∴ ? , ∴AE=AF
∴△AEF是等腰三角形, ∵AC平分∠BAD, ∴AC⊥EF (2)解:如图2所示:
∵四边形ABCD为菱形,∴CG∥AB,BO= BD=2,∵EF∥BD
∴四边形EBDG为平行四边形,∴∠G=∠ABD,∴tan∠ABD=tan∠G=
∴tan∠ABD= ,∴AO=1
解析:(1)根据菱形的性质,即可判断三角形AEF为等腰三角形,即可求出答案。 (2)根据菱形的性质,证明四边形EBDG为平行四边形,得到答案即可。
17. (1)证明:在矩形ABCD中,
∴AB//CD,AB=CD,
∵DE=BF,
∴CE=AF,且CE//AF,
∴四边形AFCE是平行四边形. (2)解:∵平行四边形AFCE是菱形,
∴AE=CE,
设AE=CE=x,
∵AB=CD=8,AD=6,∴DE=8-x,
在矩形ABCD中,∠D=90°,
∴AD2+DE2=AE2 ,
(8-x)2+62=x2,
解得 .
∴菱形的周长为25.
解析:(1)矩形的对边互相平行且相等,由DE=BF,等量代换得EC=AF,根据一组对边平行且相等求得 四边形AFCE是平行四边形。 (2)设菱形的边长为x,把DE、AE用含x的代数式表示,在Rt△ADE中,用勾股定理列式,求出x. 则菱形的周长可求。21·cn·jy·com
18. (1)证明:由题意可得,
,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴四边形 是平行四边形,
又∵
∴四边形 是菱形 (2)解:∵矩形 中, ,
∴ ,
∴ ,
∴ ,
设 ,则 ,
∵ ,
∴ ,
解得, ,
∴ ,
∴四边形 的面积是:
解析:(1)根据折叠的性质,可得∠BEC=∠BEF,EF=CE.根据两直线平行,内错角相等,可得∠FGE=∠BEF,即得∠FGE=∠FEG,由等角对等边,可得FG=EF,即得FG=EC,利用一组对边平行且相等的四边形是平行四边形,可证四边形CEFG是平行四边形,由CE=EF,即证四边形CEFG是菱形。 (2)根据矩形的矩形的性质及折叠的性质,可得∠BAF=90°,AD=BC=BF=10,由勾股定理可求AF=8,从而可得DF=2,设? ? , 则? ?,在Rt△DEF中,可得22+(6-x)2=x2,求出x的值,即得CE的长,利用平行四边形的面积公式计算即可.2·1·c·n·j·y
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
