高中数学必修一 对数的概念 教学设计
文档属性
| 名称 | 高中数学必修一 对数的概念 教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 134.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 15:08:28 | ||
图片预览

文档简介
对数的概念
一、三维目标
1、知识与技能
(1)理解对数的概念
(2)能熟练的进行指数式与对数式的互化
2、过程与方法
学生经历有指数得到对数的过程,归纳对数的定义并体会定义的合理性。体会由特殊到一般、转化划归的思想
3、情感、态度与价值观
学生经历探索、研究、体会、感受对数概念的形成和发展过程,培养学生的探索精神和学习兴趣
二、教学重难点
重点:对数的定义
难点:对数定义和对数符号的理解
三、教学过程
1、复习回顾
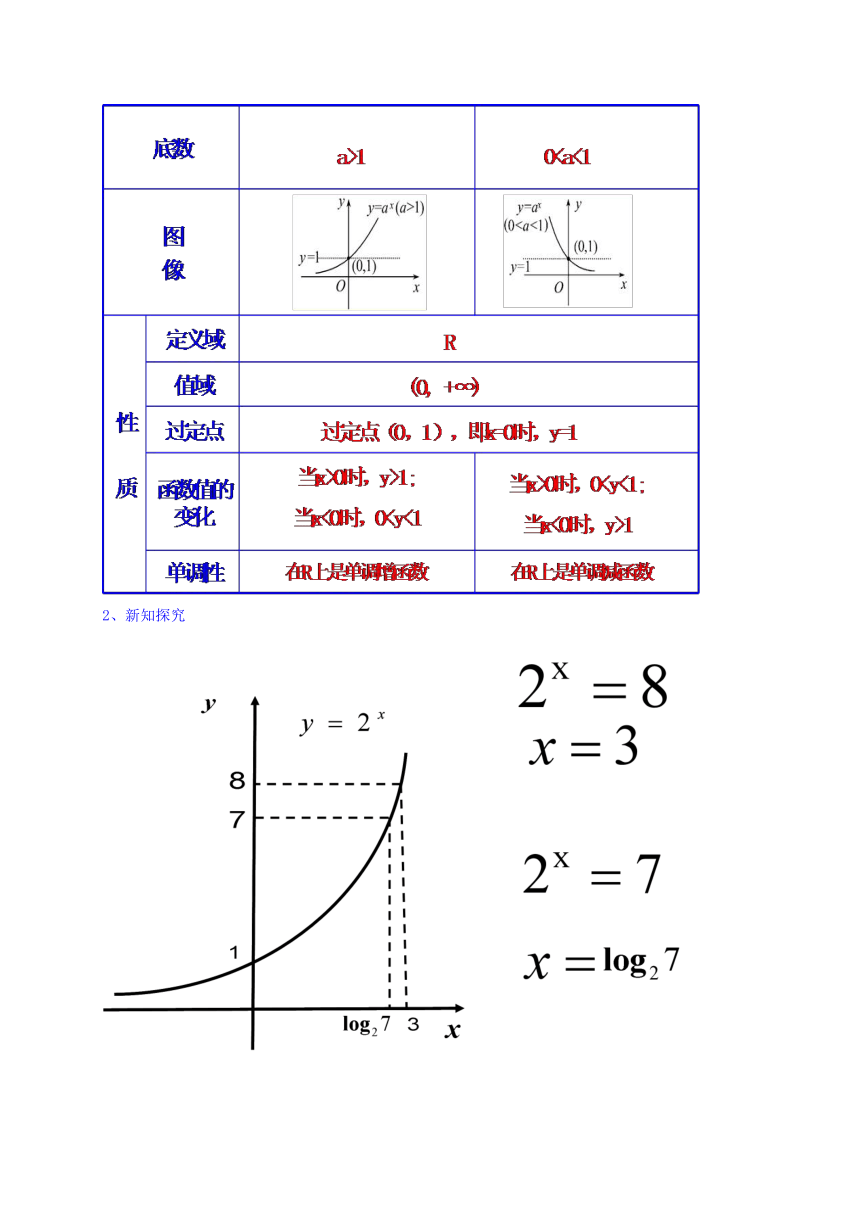
指数函数的图像与性质
2、新知探究
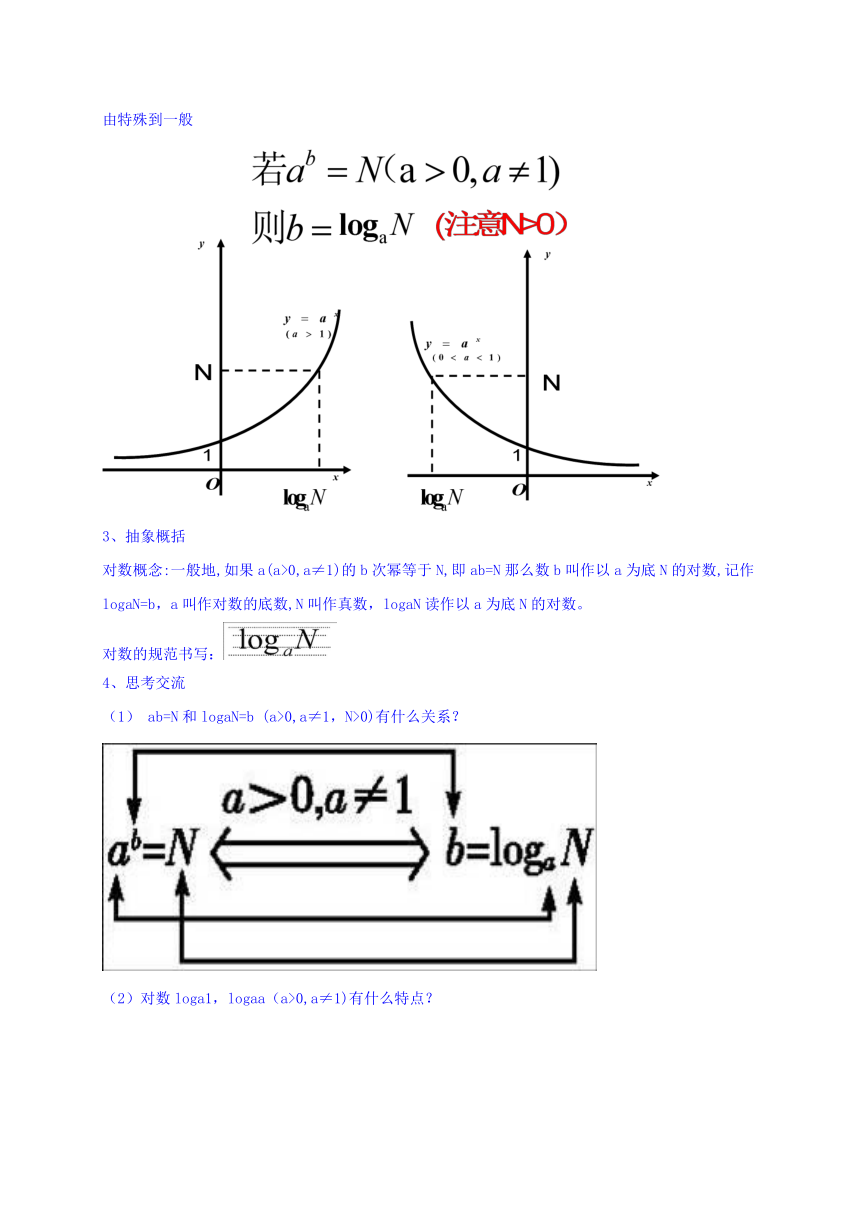
由特殊到一般
3、抽象概括
对数概念:一般地,如果a(a>0,a≠1)的b次幂等于N,即ab=N那么数b叫作以a为底N的对数,记作logaN=b,a叫作对数的底数,N叫作真数,logaN读作以a为底N的对数。
对数的规范书写:
4、思考交流
(1) ab=N和logaN=b (a>0,a≠1,N>0)有什么关系?
(2)对数loga1,logaa(a>0,a≠1)有什么特点?
(4)零和负数没有对数
5、两个常用的对数
(1)常用对数:我们通常将以10为底的对数叫作常用对数.为了简便,N的常用对数log10N简记作lgN
例如: log105 简记作lg5;log103.5 简记作lg3.5
(2)自然对数:
在科学技术中常常使用以无理e=2.718 28……为底的对数,以e为底的对数称为自然对数. 为了简便,N的自然对数 logeN简记作lnN例如: loge3简记作ln3; loge10简记作ln10
6例题讲解
例1.使对数loga(-2a+1)有意义的a的取值范围为( B )
A.a> 1/2 且a≠1 B.0 C.a>0且a≠1 D.a<1/2
例2: 将下列指数式写成对数式:
7、课堂小结
8、作业
课本80页1、2、3题
9、板书设计 对数概念....................... 例1................................. 例4..................................
..................................... ....................................... .........................................
....................................... ....................................... ..........................................
常用对数....................... 例2................................ 例5.....................................
...................................... ........................................ ............................................
.................................... ........................................ ............................................
自然对数....................... 例3...............................
....................................... .......................................
....................................... ........................................
10、课后反思
一、三维目标
1、知识与技能
(1)理解对数的概念
(2)能熟练的进行指数式与对数式的互化
2、过程与方法
学生经历有指数得到对数的过程,归纳对数的定义并体会定义的合理性。体会由特殊到一般、转化划归的思想
3、情感、态度与价值观
学生经历探索、研究、体会、感受对数概念的形成和发展过程,培养学生的探索精神和学习兴趣
二、教学重难点
重点:对数的定义
难点:对数定义和对数符号的理解
三、教学过程
1、复习回顾
指数函数的图像与性质
2、新知探究
由特殊到一般
3、抽象概括
对数概念:一般地,如果a(a>0,a≠1)的b次幂等于N,即ab=N那么数b叫作以a为底N的对数,记作logaN=b,a叫作对数的底数,N叫作真数,logaN读作以a为底N的对数。
对数的规范书写:
4、思考交流
(1) ab=N和logaN=b (a>0,a≠1,N>0)有什么关系?
(2)对数loga1,logaa(a>0,a≠1)有什么特点?
(4)零和负数没有对数
5、两个常用的对数
(1)常用对数:我们通常将以10为底的对数叫作常用对数.为了简便,N的常用对数log10N简记作lgN
例如: log105 简记作lg5;log103.5 简记作lg3.5
(2)自然对数:
在科学技术中常常使用以无理e=2.718 28……为底的对数,以e为底的对数称为自然对数. 为了简便,N的自然对数 logeN简记作lnN例如: loge3简记作ln3; loge10简记作ln10
6例题讲解
例1.使对数loga(-2a+1)有意义的a的取值范围为( B )
A.a> 1/2 且a≠1 B.0
例2: 将下列指数式写成对数式:
7、课堂小结
8、作业
课本80页1、2、3题
9、板书设计 对数概念....................... 例1................................. 例4..................................
..................................... ....................................... .........................................
....................................... ....................................... ..........................................
常用对数....................... 例2................................ 例5.....................................
...................................... ........................................ ............................................
.................................... ........................................ ............................................
自然对数....................... 例3...............................
....................................... .......................................
....................................... ........................................
10、课后反思
