北京市第四中学2018-2019学年高二下学期期中考试数学试题(Word版)
文档属性
| 名称 | 北京市第四中学2018-2019学年高二下学期期中考试数学试题(Word版) |  | |
| 格式 | zip | ||
| 文件大小 | 523.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 15:48:24 | ||
图片预览



文档简介
北京四中2018-2019学年下学期高二年级期中测试数学试卷
试卷分为两卷,卷(I)100分,卷(II)50分,满分共计150分
考试时间:120分钟
卷(I)
一、选择题:本大题共10小题,每小题4分,共40分
1. 复数(为虚数单位)在复平面内对应的点位于
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2. 下列求导正确的是
A. B.
C. D.
3. 曲线在点P(1,1)处的切线方程是
A. B.
C. D.
4. 函数=3+xlnx的单调递增区间为
A. (0,) B. (0,e)
C. (,+) D. (e,+)
5. 函数在区间(-l,+)上是减函数,则实数b的取值范围是
A. (-,-l] B. [-1,+)
C. (-,-1) D. (-1,+)
6. 当(i为虚数单位)时,的值为
A. 1 B. -1
C. i D. -i
7. 函数在区间[-1,1]上的最大值是
A. 4 B. 2[]
C. 0 D. -2
8. 函数,若其导数的图象如图所示,则函数的极小值是
A. a+b+c
B. 8a+4b+c
C. 3a+2b
D. c
9. 已知复数z满足|z|=1,则|z-i|(i为虚数单位)的最大值是
A. 0 B. 1
C. 2 D. 3
10. 函数=,若方程有且只有两个不相等的实数根,则实数a的取值范围是
A. (-,1) B. (-,1]
C. (0,1) D. [0,+)
二、填空题:本大题共6小题,每小题4分,共24分
11. 曲线在x=l处的切线的斜率是_________。
12. 函数的极大值点是_______,极大值是________。
13. 函数在区间(1,+)上是增函数,则实数a的取值范围是_______。
14. 设复数(i为虚数单位),若z为纯虚数,则实数a=_______。
15. 设函数,若的值域为R,则实数a的取值范围是_______。
16. 若函数,且<0,则实数a的取值范围是_______。
三、解答题:本大题共3小题,共36分
17. (本小题满分10分)
已知:复数与在复平面上所对应的点关于y轴对称,且(i为虚数单位),||=。
(I)求的值;
(II)若的虚部大于零,且(m,n∈R),求m,n的值。
18. (本小题满分12分)
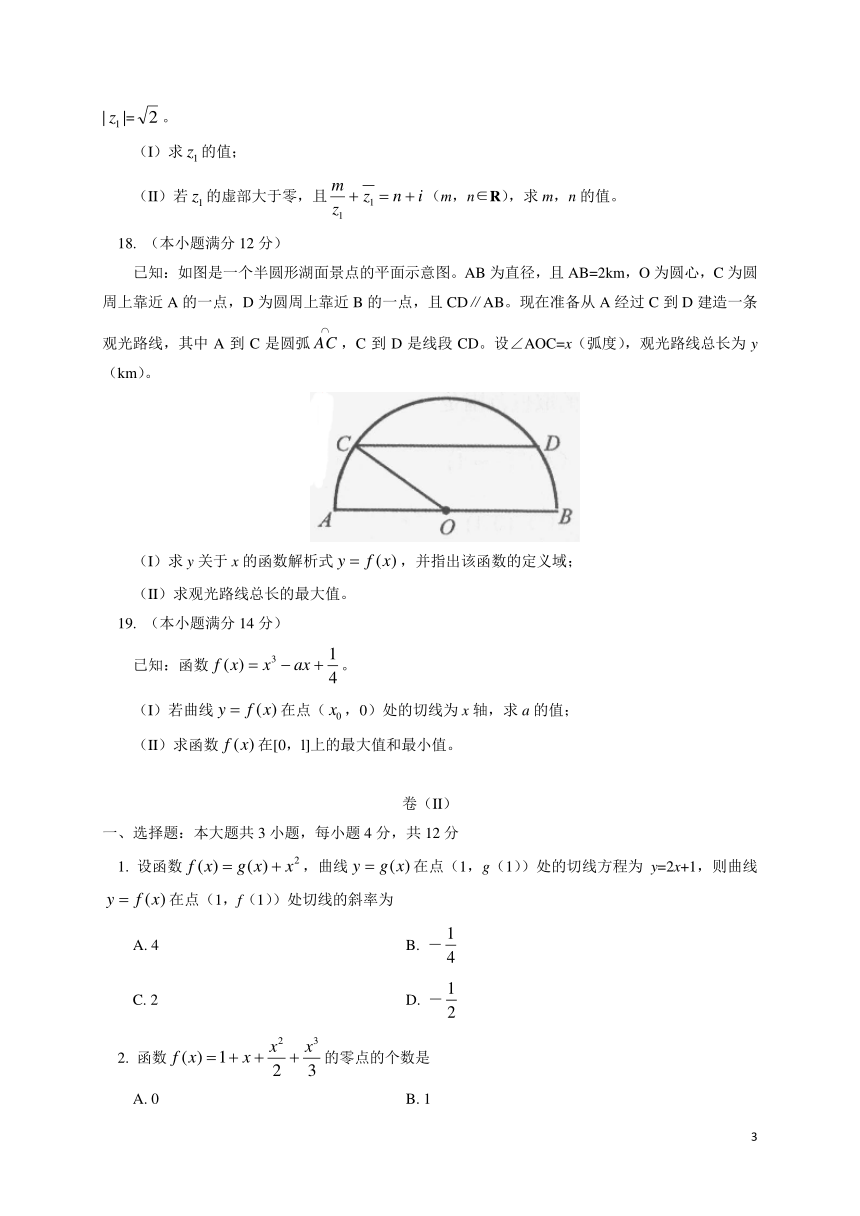
已知:如图是一个半圆形湖面景点的平面示意图。AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB。现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧,C到D是线段CD。设∠AOC=x(弧度),观光路线总长为y(km)。
(I)求y关于x的函数解析式,并指出该函数的定义域;
(II)求观光路线总长的最大值。
19. (本小题满分14分)
已知:函数。
(I)若曲线在点(,0)处的切线为x轴,求a的值;
(II)求函数在[0,l]上的最大值和最小值。
卷(II)
一、选择题:本大题共3小题,每小题4分,共12分
1. 设函数,曲线在点(1,g(1))处的切线方程为y=2x+1,则曲线在点(1,f(1))处切线的斜率为
A. 4 B. -
C. 2 D. -
2. 函数的零点的个数是
A. 0 B. 1
C. 2 D. 3
3. 设函数,则
A. 的极大值点在(-1,0)内 B. 的极大值点在(0,1)内
C. 的极小值点在(-1,0)内 D. 的极小值点在(0,1)内
二、填空题:本大题共3小题,每小题4分,共12分
4. 若复数(i为虚数单位)的实部与虚部相等,则实数a=________。
5. 已知函数(m∈R)在区间[-2,2]上有最大值3,那么在区间[-2,2]上,当x=_______时,取得最小值。
6. 已知函数满足:
(1)既有极大值,也有极小值;
(2)∈[0,1],都有>0。
请你给出一个满足上述两个条件的函数的例子________。
三、解答题:本大题共2小题,共26分
7. (本小题满分12分)
已知函数=
(I)求函数的单调区间;
(II)设函数=(x+1)lnx-x+1,证明:当x>0且x≠1时,x-1与同号。
8. (本小题满分14分)
如果函数在定义域内存在区间[a,b],使在[a,b]上的值域是[2a,2b],那么称为“倍增函数”。
(I)判断=是否为“倍增函数”,并说明理由;
(II)证明:函数=是“倍增函数”;
(III)若函数=ln()是“倍增函数”,写出实数m的取值范围。(只需写出结论)
参考答案
卷(I)
DABC ADBD CA
11. 2e; 12. 2,16: 13. a≥-3; 14. -8;
15. (-,-1][2,+); 16. (-,-1);
17. 解:(I)设(x,y∈R),则z2=-x+yi,
∵z1(1-i)=z2(1+i),|z1|=,∴,
∴或,即或 ……………………6分
(II)∵z1的虚部大于零,∴,∴,
则有,∴,∴。………10分
18. 解:(I)由题意知,=,…………………………………2分
CD=2cosx, …………………………………4分
因为C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,
所以0
(II)记=x+2cosx,则=l-2sinx,………………………………7分
令=0,得x=,………………………………………………8分
当x变化时,与的变化情况如下表:
x (0,) (,)
+ 0 -
↗ 极大值 ↘
…………………………………10分
所以函数在x=处取得极大值,这个极大值就是最大值, …………11分
即()=+,
答:观光路线总长的最大值为+千米。 ……………………………12分
19. 解:(I)由于x轴为的切线,则,……①……1分
又=0,即3=0, ……②……3分
②代入①,解得=,所以a=。……5分
(II)=,
①当a≤0时,≥0,在[0,1]单调递增,
所以x=0时,取得最小值。
x=1时,取得最大值。 ……7分
②当a≥3时,<0,在[0,1]单调递减,
所以,x=1时,取得最小值。
x=0时,取得最大值。 ……9分
③当0
x (0,) (,1)
- 0 +
↘ 极小值 ↗
由上表可知,当时,取得最小值;………12分
由于,,
当0
卷(Ⅱ)
A B A 4. -1; 5. -2; 6. ,
7. 解:(I)函数的定义域是(0,+),
又=,令=0,得x=1,
当x变化时,与的变化情况如下表:
x (0,1) 1 (1,+)
- 0 +
↘ ↗
所以,的增区间是(1,+),减区间是(0,1) …………………6分
(II)函数的定义域是(0,+),又=lnx+=lnx+=,
由(I)可知,==1,所以,当x>0时,>0,
所以,在区间(0,+)上单调递增。
因为,
所以当x>1时,>且x-1>0;
当0
8. 解:(I)=是“倍增函数”,理由如下:
=的定义域是R,且在[0,+)上单调递增;
所以,当[0,2]时,∈[0,4],
所以,=是“倍增函数”。 …………………………………4分
(II)=的定义域是R。
当x>0时,=>0,所以在区间(0,+)上单调递增。
设=-2x=,=。
设h(x)==,=>0,
所以,h(x)在区间(-,+)上单调递增。
又h(0)=-2<0,h(1)=e-1>0,
所以,存在唯一的∈(0,1),使得h()==0,
所以,当x变化时,与的变化情况如下表:
x (-,) (,+)
- 0 +
↘ ↗
因为g(1)=e-3<0,g(2)=>0,
所以,存在唯一的∈(1,2),使得=0,
又=0,所以函数只有两个零点,即0与。
所以=0,=2。
结合在区间(0,+)上单调递增可知,当x∈[0,]时的值域是[0,2]。
所以,令[a,b]=[0,],=是“倍增函数”。………………11分
(III)
PAGE
2
同课章节目录
