27.2.1相似三角形的判定 第1课时平行线分线段成比例 同步课件
文档属性
| 名称 | 27.2.1相似三角形的判定 第1课时平行线分线段成比例 同步课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
27.2 相似三角形
27.2.1 相似三角形的判定
课程讲授
新知导入
随堂练习
课堂小结
第1课时 平行线分线段成比例
第二十七章 相似
知识要点
1.相似三角形的有关概念
2.平行线分线段成比例及其推论
3.相似三角形判定的预备定理
新知导入
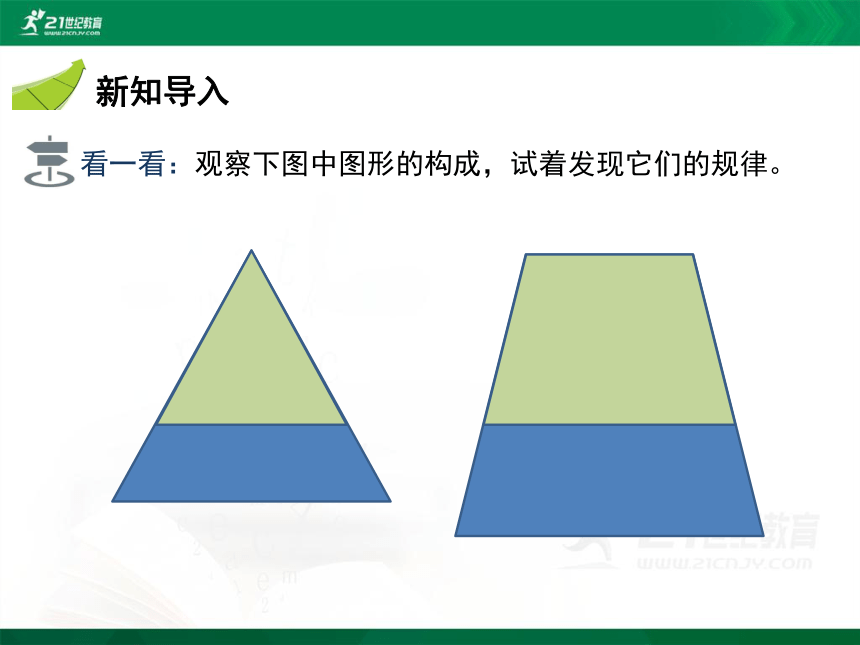
看一看:观察下图中图形的构成,试着发现它们的规律。
课程讲授
1
相似三角形的有关概念
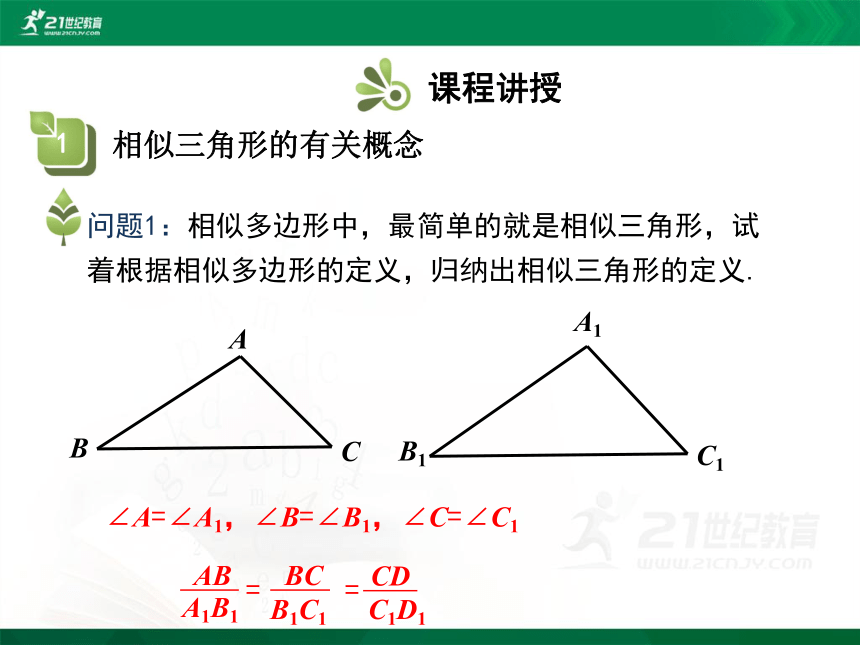
问题1:相似多边形中,最简单的就是相似三角形,试着根据相似多边形的定义,归纳出相似三角形的定义.
A
B
C
A1
B1
C1
∠A=∠A1,∠B=∠B1,∠C=∠C1
B1C1
AB
A1B1
BC
=
=
C1D1
CD
1
相似三角形的有关概念
A
B
C
A1
B1
C1
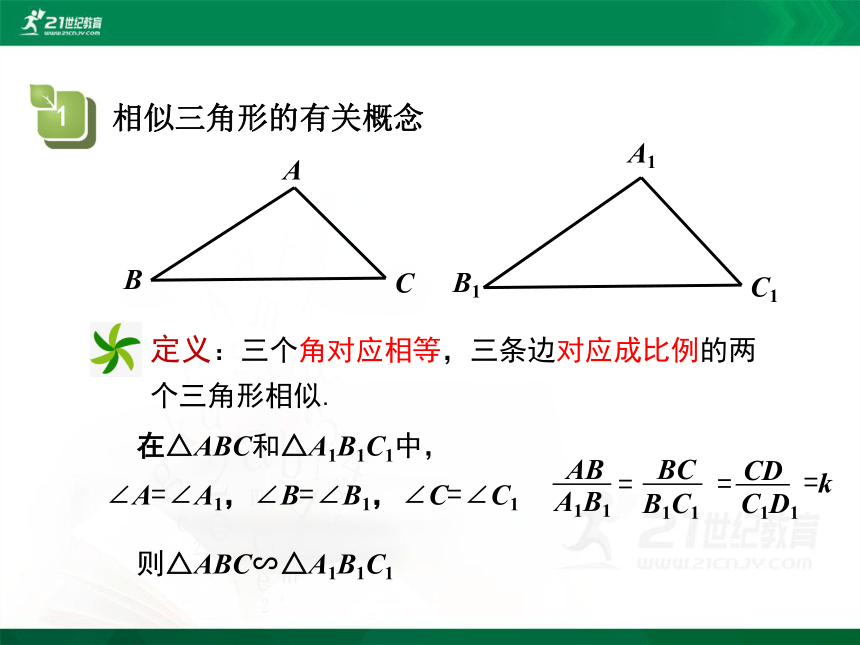
定义:三个角对应相等,三条边对应成比例的两个三角形相似.
在△ABC和△A1B1C1中,
∠A=∠A1,∠B=∠B1,∠C=∠C1
B1C1
AB
A1B1
BC
=
=
C1D1
CD
=k
则△ABC∽△A1B1C1
1
相似三角形的有关概念
练一练:如图,△ABC∽△AED,∠AED=∠B,那么下列比例式成立的是( )
A.
B.
C.
D.
A
2
平行线分线段成比例及其推论
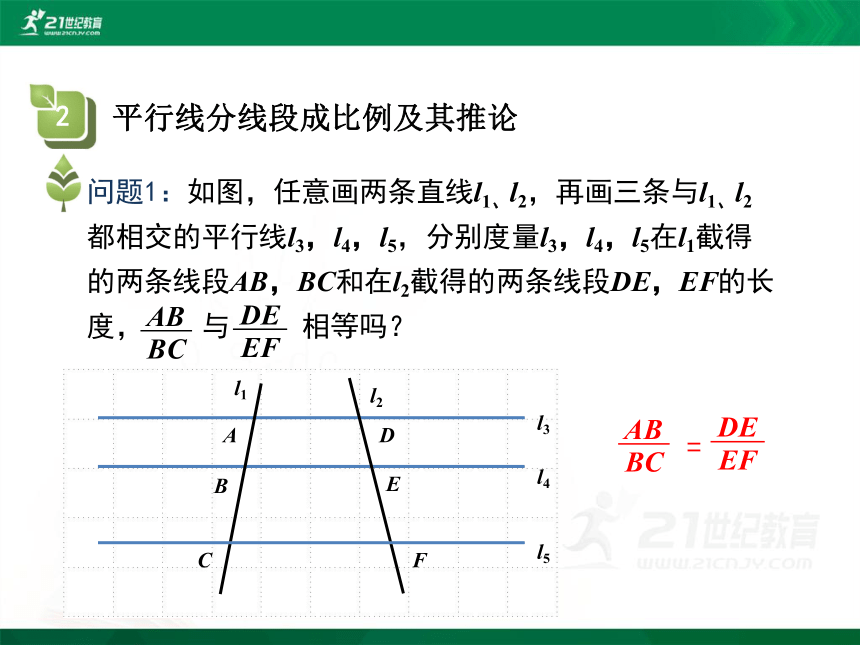
问题1:如图,任意画两条直线l1、l2,再画三条与l1、l2都相交的平行线l3,l4,l5,分别度量l3,l4,l5在l1截得的两条线段AB,BC和在l2截得的两条线段DE,EF的长度, 与 相等吗?
AB
BC
DE
EF
l2
l1
l4
l3
l5
A
B
C
D
E
F
AB
BC
DE
EF
=
2
平行线分线段成比例及其推论
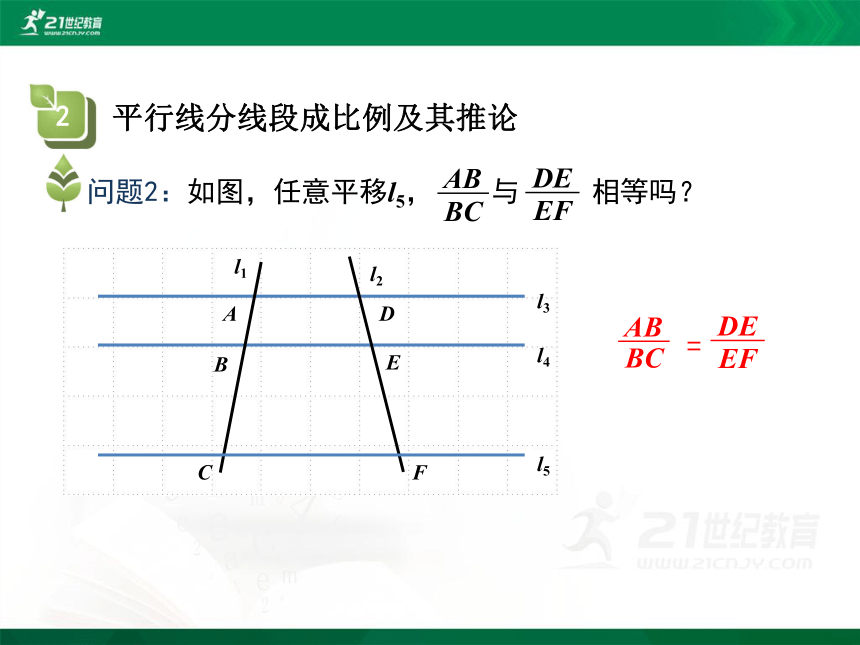
问题2:如图,任意平移l5, 与 相等吗?
AB
BC
DE
EF
l2
l1
l4
l3
l5
A
B
C
D
E
F
AB
BC
DE
EF
=
2
平行线分线段成比例及其推论
归纳: 一般地,我们有平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段______.
成比例
2
平行线分线段成比例及其推论
l1
l2
l4
l3
l5
A
D
B
E
C
把平行线分线段成比例的基本事实应用到三角形中,会出现以下两种情况:
把l4看成平行△ABC的边BC的直线
2
平行线分线段成比例及其推论
l1
l2
l4
l3
l5
A
B
C
D
E
把平行线分线段成比例的基本事实应用到三角形中,会出现以下两种情况:
把l3看成平行△ABC的边BC的直线
2
平行线分线段成比例及其推论
归纳:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段______.
成比例
2
平行线分线段成比例及其推论
练一练:如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A.
B.
C.
D.
A
3
相似三角形判定的预备定理
问题1:如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.△ADE与△ABC的三个角分别相等吗?
B
C
A
D
E
∠A=∠A,∠B=∠D,∠C=∠E
3
相似三角形判定的预备定理
问题2:如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
B
C
A
D
E
CA
AD
DE
EA
AB
BC
=
=
3
相似三角形判定的预备定理
问题3:如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
B
C
A
D
E
△ADE∽△ABC
平行移动DE的位置,结论还成立
D'
E'
△AD'E'∽△ABC
△ADE∽△ABC,且只要DE∥BC,这个结论恒成立.
我们发现:
3
相似三角形判定的预备定理
问题3:试着运用所学知识证明你的结论.
B
C
A
D
E
证明:在△ADE与△ABC中,∠A=∠A.
∴ ∠ADE=∠B,∠AED=∠C.
∵ DE∥BC,
过点D作DF∥AC,交BC于点F.
再证明两个三角形的边成比例,
F
∵ DE∥BC,DF∥AC,
AC
AD
AE
AB
=
BF
BC
=
AC
AE
∴
∵ 四边形DFCE为平行四边形,
∴ DE=FC,
∴
BC
AD
AE
DE
AB
AC
=
=
∴△ADE∽△ABC
3
相似三角形判定的预备定理
相似三角形判定的预备定理:
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形______.
相似
3
相似三角形判定的预备定理
练一练:如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则下列结论正确的是( )
A.
B.
C.
D.
B
随堂练习
1.已知△ABC和△A′B′C′相似,且△ABC与△A′B′C′的相似比为R1,△A′B′C′与△ABC的相似比为R2,则R1与R2的关系是( )
A.R1=R2
B.R1R2=-1
C.R1+R2=0
D.R1R2=1
D
2.如图,在平行四边形ABCD中,点E是边AD 的中点,EC交对角线BD于点F,则EF∶FC等于( )
A.3∶2
B.3∶1
C.1∶1
D.1∶2
B
3.如图,在△ABC中,DE∥BC, ,则 =_____.
=
AB
AD
1
3
1
3
AC
AE
4.如图,AB∥DE,若AC=4,BC=2,DC=1,则EC=_______.
2
5.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F.已知 = ,求 的值.
AC
3
AB
1
DE
EF
解:∵l1∥l2∥l3,
∴ = = ,
AC
AB
DF
DE
3
1
∴ =2.
DE
EF
6.如图,在△ABC中,DE∥BC,DF∥AB,
求证:△ADE∽△DCF.
∴△ADE∽△DCF.
证明:∵DE∥BC,
∴△ADE∽△ACB.
∵DF∥AB,
∴△DCF∽△ACB.
课堂小结
平行线分线段成比例
相似三角形
三个角对应相等,三条边对应成比例的三角形相似
平行线分线段成比例及其推论
两条直线被一组平行线所截,所得的对应线段成比例
相似三角形判定的预备定理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
27.2 相似三角形
27.2.1 相似三角形的判定
课程讲授
新知导入
随堂练习
课堂小结
第1课时 平行线分线段成比例
第二十七章 相似
知识要点
1.相似三角形的有关概念
2.平行线分线段成比例及其推论
3.相似三角形判定的预备定理
新知导入
看一看:观察下图中图形的构成,试着发现它们的规律。
课程讲授
1
相似三角形的有关概念
问题1:相似多边形中,最简单的就是相似三角形,试着根据相似多边形的定义,归纳出相似三角形的定义.
A
B
C
A1
B1
C1
∠A=∠A1,∠B=∠B1,∠C=∠C1
B1C1
AB
A1B1
BC
=
=
C1D1
CD
1
相似三角形的有关概念
A
B
C
A1
B1
C1
定义:三个角对应相等,三条边对应成比例的两个三角形相似.
在△ABC和△A1B1C1中,
∠A=∠A1,∠B=∠B1,∠C=∠C1
B1C1
AB
A1B1
BC
=
=
C1D1
CD
=k
则△ABC∽△A1B1C1
1
相似三角形的有关概念
练一练:如图,△ABC∽△AED,∠AED=∠B,那么下列比例式成立的是( )
A.
B.
C.
D.
A
2
平行线分线段成比例及其推论
问题1:如图,任意画两条直线l1、l2,再画三条与l1、l2都相交的平行线l3,l4,l5,分别度量l3,l4,l5在l1截得的两条线段AB,BC和在l2截得的两条线段DE,EF的长度, 与 相等吗?
AB
BC
DE
EF
l2
l1
l4
l3
l5
A
B
C
D
E
F
AB
BC
DE
EF
=
2
平行线分线段成比例及其推论
问题2:如图,任意平移l5, 与 相等吗?
AB
BC
DE
EF
l2
l1
l4
l3
l5
A
B
C
D
E
F
AB
BC
DE
EF
=
2
平行线分线段成比例及其推论
归纳: 一般地,我们有平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段______.
成比例
2
平行线分线段成比例及其推论
l1
l2
l4
l3
l5
A
D
B
E
C
把平行线分线段成比例的基本事实应用到三角形中,会出现以下两种情况:
把l4看成平行△ABC的边BC的直线
2
平行线分线段成比例及其推论
l1
l2
l4
l3
l5
A
B
C
D
E
把平行线分线段成比例的基本事实应用到三角形中,会出现以下两种情况:
把l3看成平行△ABC的边BC的直线
2
平行线分线段成比例及其推论
归纳:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段______.
成比例
2
平行线分线段成比例及其推论
练一练:如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A.
B.
C.
D.
A
3
相似三角形判定的预备定理
问题1:如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.△ADE与△ABC的三个角分别相等吗?
B
C
A
D
E
∠A=∠A,∠B=∠D,∠C=∠E
3
相似三角形判定的预备定理
问题2:如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
B
C
A
D
E
CA
AD
DE
EA
AB
BC
=
=
3
相似三角形判定的预备定理
问题3:如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
B
C
A
D
E
△ADE∽△ABC
平行移动DE的位置,结论还成立
D'
E'
△AD'E'∽△ABC
△ADE∽△ABC,且只要DE∥BC,这个结论恒成立.
我们发现:
3
相似三角形判定的预备定理
问题3:试着运用所学知识证明你的结论.
B
C
A
D
E
证明:在△ADE与△ABC中,∠A=∠A.
∴ ∠ADE=∠B,∠AED=∠C.
∵ DE∥BC,
过点D作DF∥AC,交BC于点F.
再证明两个三角形的边成比例,
F
∵ DE∥BC,DF∥AC,
AC
AD
AE
AB
=
BF
BC
=
AC
AE
∴
∵ 四边形DFCE为平行四边形,
∴ DE=FC,
∴
BC
AD
AE
DE
AB
AC
=
=
∴△ADE∽△ABC
3
相似三角形判定的预备定理
相似三角形判定的预备定理:
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形______.
相似
3
相似三角形判定的预备定理
练一练:如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则下列结论正确的是( )
A.
B.
C.
D.
B
随堂练习
1.已知△ABC和△A′B′C′相似,且△ABC与△A′B′C′的相似比为R1,△A′B′C′与△ABC的相似比为R2,则R1与R2的关系是( )
A.R1=R2
B.R1R2=-1
C.R1+R2=0
D.R1R2=1
D
2.如图,在平行四边形ABCD中,点E是边AD 的中点,EC交对角线BD于点F,则EF∶FC等于( )
A.3∶2
B.3∶1
C.1∶1
D.1∶2
B
3.如图,在△ABC中,DE∥BC, ,则 =_____.
=
AB
AD
1
3
1
3
AC
AE
4.如图,AB∥DE,若AC=4,BC=2,DC=1,则EC=_______.
2
5.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F.已知 = ,求 的值.
AC
3
AB
1
DE
EF
解:∵l1∥l2∥l3,
∴ = = ,
AC
AB
DF
DE
3
1
∴ =2.
DE
EF
6.如图,在△ABC中,DE∥BC,DF∥AB,
求证:△ADE∽△DCF.
∴△ADE∽△DCF.
证明:∵DE∥BC,
∴△ADE∽△ACB.
∵DF∥AB,
∴△DCF∽△ACB.
课堂小结
平行线分线段成比例
相似三角形
三个角对应相等,三条边对应成比例的三角形相似
平行线分线段成比例及其推论
两条直线被一组平行线所截,所得的对应线段成比例
相似三角形判定的预备定理
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
