27.2.1相似三角形的判定 第2课时相似三角形的判定定理1,2 同步课件
文档属性
| 名称 | 27.2.1相似三角形的判定 第2课时相似三角形的判定定理1,2 同步课件 |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 11:54:28 | ||
图片预览



文档简介
(共26张PPT)
27.2 相似三角形
27.2.1 相似三角形的判定
课程讲授
新知导入
随堂练习
课堂小结
第2课时 相似三角形的判定定理1,2
第二十七章 相似
知识要点
1.三边成比例的两个三角形相似
2.两边成比例且夹角相等的两个三角形相似
新知导入
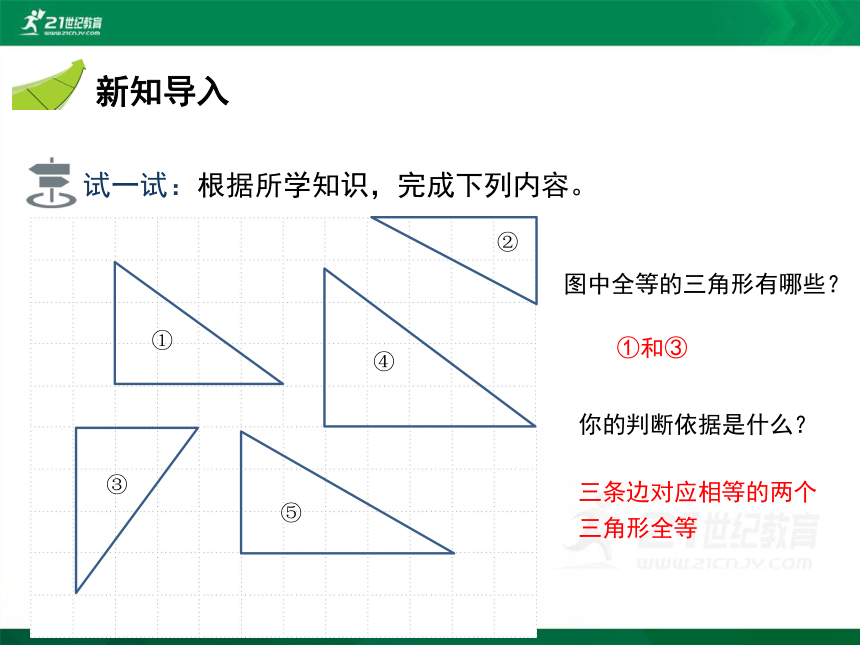
试一试:根据所学知识,完成下列内容。
图中全等的三角形有哪些?
①
③
⑤
④
②
①和③
你的判断依据是什么?
三条边对应相等的两个三角形全等
课程讲授
1
三边成比例的两个三角形相似
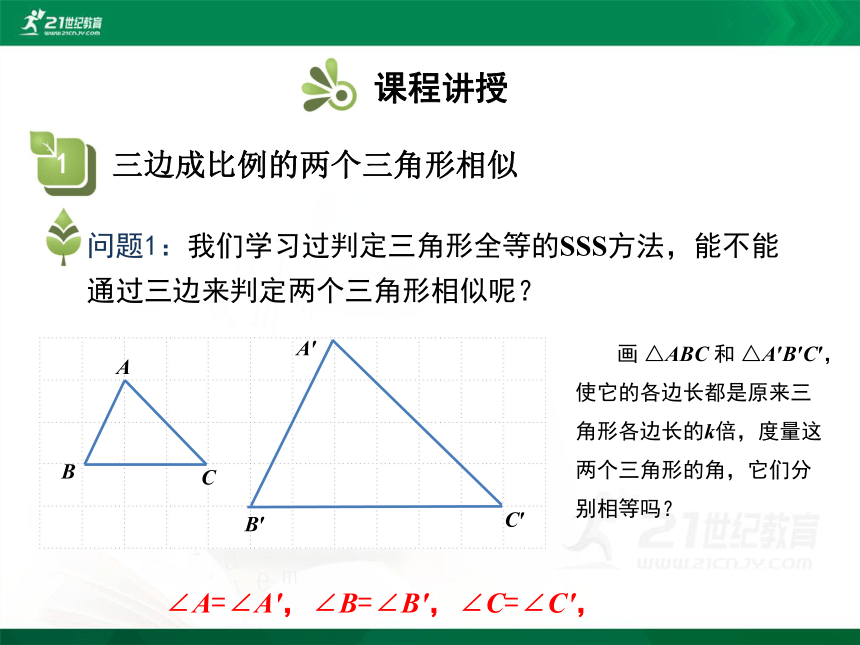
问题1:我们学习过判定三角形全等的SSS方法,能不能通过三边来判定两个三角形相似呢?
画 △ABC 和 △A′B′C′,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的角,它们分别相等吗?
B
A
C
C′
A′
B′
∠A=∠A',∠B=∠B',∠C=∠C',
1
三边成比例的两个三角形相似
B
A
C
C′
A′
B′
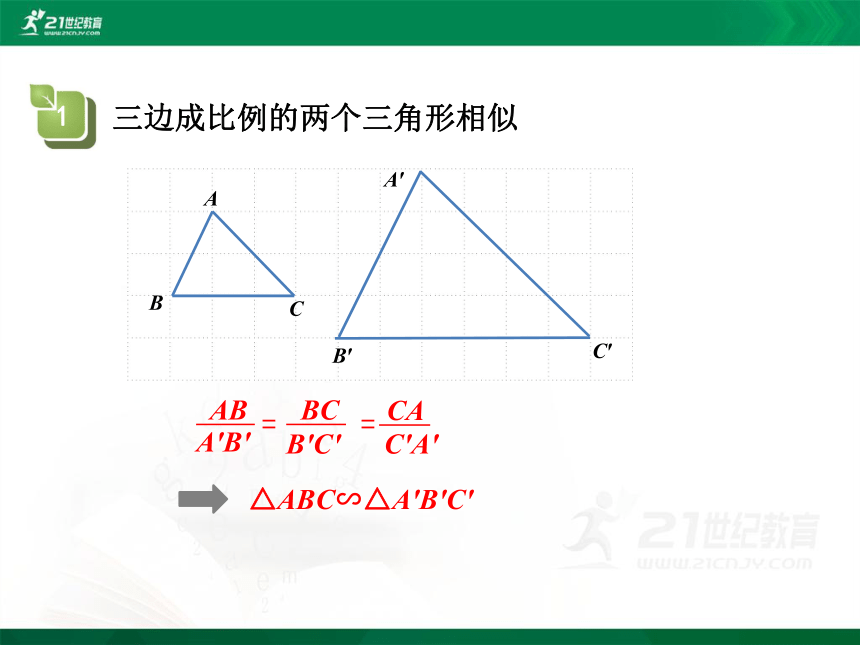
B'C'
AB
A'B'
BC
=
=
C'A'
CA
△ABC∽△A'B'C'
1
三边成比例的两个三角形相似
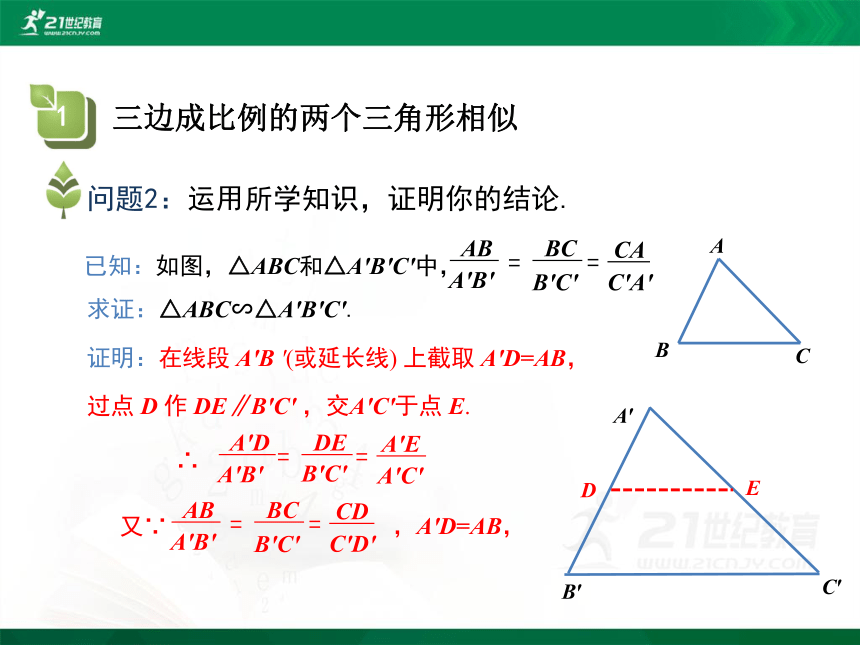
问题2:运用所学知识,证明你的结论.
B
A
C
C′
A′
B′
已知:如图,△ABC和△A'B'C'中,
B'C'
AB
A'B'
BC
=
=
C'A'
CA
求证:△ABC∽△A'B'C'.
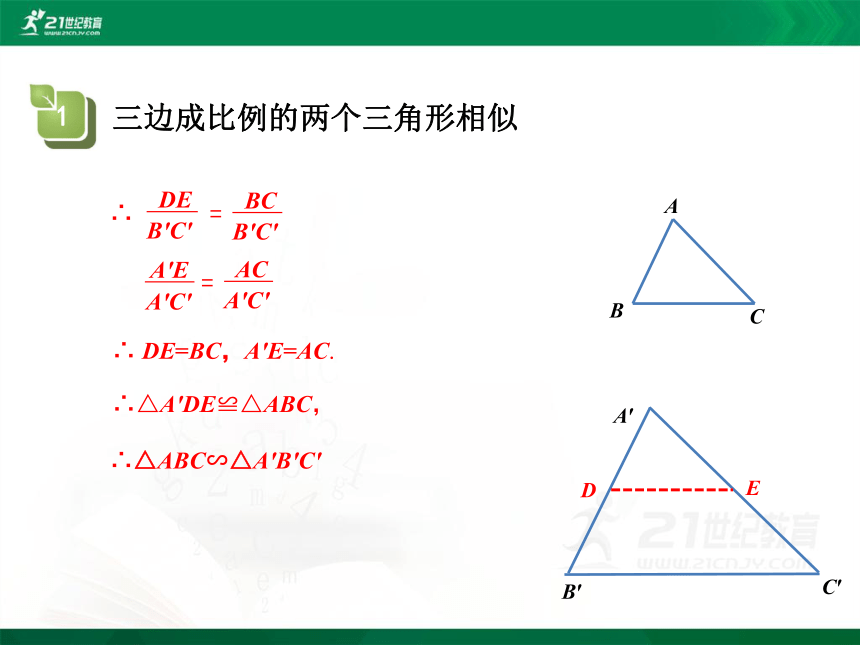
证明:在线段 A'B '(或延长线) 上截取 A'D=AB,过点 D 作 DE∥B'C' ,交A'C'于点 E.
E
D
B'C'
A'D
A'B'
DE
=
=
A'C'
A'E
∴
又∵
B'C'
AB
A'B'
BC
=
=
C'D'
CD
,A'D=AB,
1
三边成比例的两个三角形相似
B
A
C
C′
A′
B′
E
D
∴
B'C'
DE
=
B'C'
BC
A'C'
A'E
=
A'C'
AC
∴ DE=BC,A'E=AC.
∴△A′DE≌△ABC,
∴△ABC∽△A'B'C'
1
三边成比例的两个三角形相似
B
A
C
C′
A′
B′
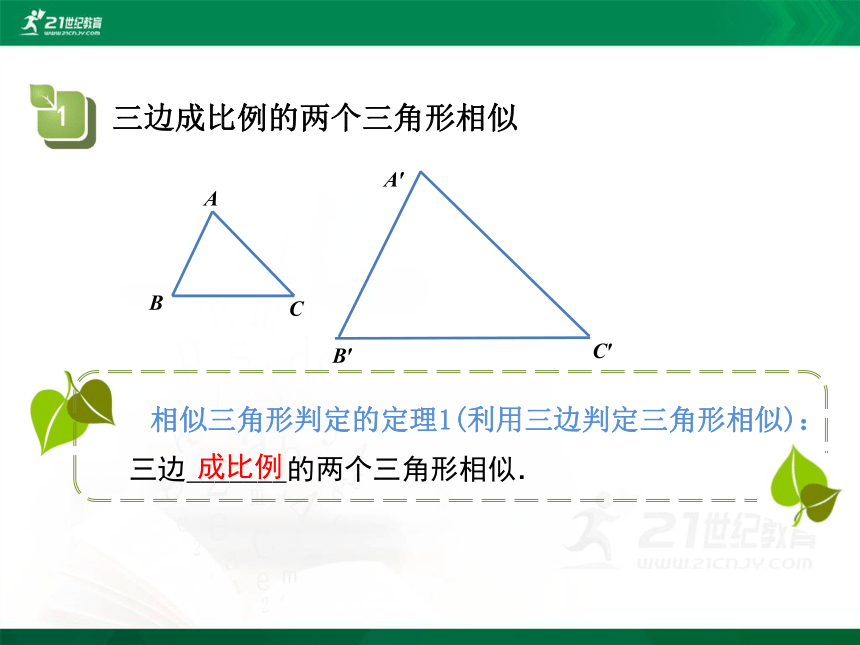
相似三角形判定的定理1(利用三边判定三角形相似):
三边_______的两个三角形相似.
成比例
例 根据下列条件,判断 △ABC 和 △A′B′C′ 是否相似,并说明理由:
AB =4cm, BC =6cm, AC=8cm,
A'B' =12cm, B'C' =18cm, A'C'=24cm,;
1
三边成比例的两个三角形相似
解:∵
AB
A'B'
=
4
12
=
1
3
BC
B'C'
=
6
18
=
1
3
AC
A'C'
=
8
24
=
1
3
B'C'
AB
A'B'
BC
=
=
C'A'
CA
∴
∴△ABC∽△A'B'C'
1
三边成比例的两个三角形相似
练一练:有甲、乙两个三角形木框,甲三角形木框的三边长分别为1, , ,乙三角形木框的三边长分别为5, , ,则甲、乙两个三角形( )
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断
A
2
两边成比例且夹角相等的两个三角形相似
问题1:我们学习过判定三角形全等的SAS方法,能不能通过两边和夹角来判定两个三角形相似呢?
画 △ABC 和 △A′B′C′,使∠A=∠A′,夹角的两边边长都是原来三角形边长的k倍,度量这两个三角形的另外的两个角,它们分别相等吗?
B
A
C
C′
A′
B′
∠B=∠B',∠C=∠C',
∠A=∠A'
2
两边成比例且夹角相等的两个三角形相似
B
A
C
C′
A′
B′
∠A=∠A'
AB
A'B'
=
C'A'
CA
△ABC∽△A'B'C'
2
两边成比例且夹角相等的两个三角形相似
问题2:运用所学知识,证明你的结论.
已知:如图,△ABC和△A'B'C'中,∠A=∠A'
AB
A'B'
=
C'A'
CA
求证:△ABC∽△A'B'C'.
B
A
C
C′
A′
B′
证明:在 △A′B′C′ 的边 A′B′ 上截取点D,使 A′D = AB.过点 D 作 DE∥B′C′,交 A′C′ 于点 E.
E
D
∵ DE∥B′C′,
∴ △A′DE∽△A′B′C′.
2
两边成比例且夹角相等的两个三角形相似
B
A
C
C′
A′
B′
E
D
∴
A'C'
A'E
=
A'B'
A'D
∵ A′D=AB,
AB
A'B'
=
C'A'
CA
∴
A'B'
A'D
=
A'C'
A'E
=
C'A'
CA
又∵ ∠A′ = ∠A.
∴ A′E = AC .
∴ △A′DE ≌ △ABC,
∴ △A′B′C′ ∽ △ABC.
2
两边成比例且夹角相等的两个三角形相似
B
A
C
C′
A′
B′
相似三角形判定的定理2(利用两边和夹角判定三角形相似):
两边_______且夹角______的两个三角形相似.
成比例
相等
2
两边成比例且夹角相等的两个三角形相似
例 根据下列条件,判断 △ABC 和 △A′B′C′ 是否相似,并说明理由:
∠A=120°,AB=7 cm,AC=14 cm,
∠A′=120°,A′B′=3 cm ,A′C′=6 cm.
解:∵
AB
A'B'
=
7
3
AC
A'C'
=
14
6
=
7
3
A'C'
AB
A'B'
AC
=
∴
又∵ ∠A′ = ∠A.
∴ △A′B′C′ ∽ △ABC.
2
两边成比例且夹角相等的两个三角形相似
练一练:如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.
B.
C.
D.
C
随堂练习
1.已知△ABC的三边长分别为6 cm,7.5 cm,9 cm,△DEF的一边长为4 cm,当另两边的长是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm
B.4 cm,5 cm
C.5 cm,6 cm
D.6 cm,7 cm
C
2.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
B
3.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
D
4.如图,在△ABC中,AB=25,BC=40,AC=20;在△ADE中,AE=12,AD=15,DE=24.试判断这两个三角形是否相似,并说明理由.
解:相似.
理由如下:
∵ = = ,
AC
20
5
AE
12
3
= = ,
AB
25
5
AD
15
3
= = ,
BC
40
5
DE
24
3
∴△ABC∽△ADE.
∴ = = ,
AC
AE
AB
AD
BC
DE
5.如图,已知AD·AC=AB·AE.
(1)求证:△ADE∽△ABC;
∴△ADE∽△ABC.
证明:∵AD·AC=AB·AE,
在△ADE与△ABC 中,
∴ = .
AD
AE
AB
AC
∵ = ,
AD
AE
AB
AC
∠A=∠A,
5.如图,已知AD·AC=AB·AE.
(2)若∠A=45°,∠C=95°,求∠ADE的度数.
∴∠ADE=40°.
解:∵△ADE∽△ABC,
∴∠ADE=∠B.
∵∠A=45°,∠C=95°,
∴∠B=180°-∠A-∠C
=40°,
课堂小结
相似三角形的判定
判定定理1
判定定理2
三边成比例的两个三角形相似.
两边成比例且夹角相等的两个三角形相似.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
27.2 相似三角形
27.2.1 相似三角形的判定
课程讲授
新知导入
随堂练习
课堂小结
第2课时 相似三角形的判定定理1,2
第二十七章 相似
知识要点
1.三边成比例的两个三角形相似
2.两边成比例且夹角相等的两个三角形相似
新知导入
试一试:根据所学知识,完成下列内容。
图中全等的三角形有哪些?
①
③
⑤
④
②
①和③
你的判断依据是什么?
三条边对应相等的两个三角形全等
课程讲授
1
三边成比例的两个三角形相似
问题1:我们学习过判定三角形全等的SSS方法,能不能通过三边来判定两个三角形相似呢?
画 △ABC 和 △A′B′C′,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的角,它们分别相等吗?
B
A
C
C′
A′
B′
∠A=∠A',∠B=∠B',∠C=∠C',
1
三边成比例的两个三角形相似
B
A
C
C′
A′
B′
B'C'
AB
A'B'
BC
=
=
C'A'
CA
△ABC∽△A'B'C'
1
三边成比例的两个三角形相似
问题2:运用所学知识,证明你的结论.
B
A
C
C′
A′
B′
已知:如图,△ABC和△A'B'C'中,
B'C'
AB
A'B'
BC
=
=
C'A'
CA
求证:△ABC∽△A'B'C'.
证明:在线段 A'B '(或延长线) 上截取 A'D=AB,过点 D 作 DE∥B'C' ,交A'C'于点 E.
E
D
B'C'
A'D
A'B'
DE
=
=
A'C'
A'E
∴
又∵
B'C'
AB
A'B'
BC
=
=
C'D'
CD
,A'D=AB,
1
三边成比例的两个三角形相似
B
A
C
C′
A′
B′
E
D
∴
B'C'
DE
=
B'C'
BC
A'C'
A'E
=
A'C'
AC
∴ DE=BC,A'E=AC.
∴△A′DE≌△ABC,
∴△ABC∽△A'B'C'
1
三边成比例的两个三角形相似
B
A
C
C′
A′
B′
相似三角形判定的定理1(利用三边判定三角形相似):
三边_______的两个三角形相似.
成比例
例 根据下列条件,判断 △ABC 和 △A′B′C′ 是否相似,并说明理由:
AB =4cm, BC =6cm, AC=8cm,
A'B' =12cm, B'C' =18cm, A'C'=24cm,;
1
三边成比例的两个三角形相似
解:∵
AB
A'B'
=
4
12
=
1
3
BC
B'C'
=
6
18
=
1
3
AC
A'C'
=
8
24
=
1
3
B'C'
AB
A'B'
BC
=
=
C'A'
CA
∴
∴△ABC∽△A'B'C'
1
三边成比例的两个三角形相似
练一练:有甲、乙两个三角形木框,甲三角形木框的三边长分别为1, , ,乙三角形木框的三边长分别为5, , ,则甲、乙两个三角形( )
A.一定相似
B.一定不相似
C.不一定相似
D.无法判断
A
2
两边成比例且夹角相等的两个三角形相似
问题1:我们学习过判定三角形全等的SAS方法,能不能通过两边和夹角来判定两个三角形相似呢?
画 △ABC 和 △A′B′C′,使∠A=∠A′,夹角的两边边长都是原来三角形边长的k倍,度量这两个三角形的另外的两个角,它们分别相等吗?
B
A
C
C′
A′
B′
∠B=∠B',∠C=∠C',
∠A=∠A'
2
两边成比例且夹角相等的两个三角形相似
B
A
C
C′
A′
B′
∠A=∠A'
AB
A'B'
=
C'A'
CA
△ABC∽△A'B'C'
2
两边成比例且夹角相等的两个三角形相似
问题2:运用所学知识,证明你的结论.
已知:如图,△ABC和△A'B'C'中,∠A=∠A'
AB
A'B'
=
C'A'
CA
求证:△ABC∽△A'B'C'.
B
A
C
C′
A′
B′
证明:在 △A′B′C′ 的边 A′B′ 上截取点D,使 A′D = AB.过点 D 作 DE∥B′C′,交 A′C′ 于点 E.
E
D
∵ DE∥B′C′,
∴ △A′DE∽△A′B′C′.
2
两边成比例且夹角相等的两个三角形相似
B
A
C
C′
A′
B′
E
D
∴
A'C'
A'E
=
A'B'
A'D
∵ A′D=AB,
AB
A'B'
=
C'A'
CA
∴
A'B'
A'D
=
A'C'
A'E
=
C'A'
CA
又∵ ∠A′ = ∠A.
∴ A′E = AC .
∴ △A′DE ≌ △ABC,
∴ △A′B′C′ ∽ △ABC.
2
两边成比例且夹角相等的两个三角形相似
B
A
C
C′
A′
B′
相似三角形判定的定理2(利用两边和夹角判定三角形相似):
两边_______且夹角______的两个三角形相似.
成比例
相等
2
两边成比例且夹角相等的两个三角形相似
例 根据下列条件,判断 △ABC 和 △A′B′C′ 是否相似,并说明理由:
∠A=120°,AB=7 cm,AC=14 cm,
∠A′=120°,A′B′=3 cm ,A′C′=6 cm.
解:∵
AB
A'B'
=
7
3
AC
A'C'
=
14
6
=
7
3
A'C'
AB
A'B'
AC
=
∴
又∵ ∠A′ = ∠A.
∴ △A′B′C′ ∽ △ABC.
2
两边成比例且夹角相等的两个三角形相似
练一练:如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.
B.
C.
D.
C
随堂练习
1.已知△ABC的三边长分别为6 cm,7.5 cm,9 cm,△DEF的一边长为4 cm,当另两边的长是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm
B.4 cm,5 cm
C.5 cm,6 cm
D.6 cm,7 cm
C
2.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
B
3.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
D
4.如图,在△ABC中,AB=25,BC=40,AC=20;在△ADE中,AE=12,AD=15,DE=24.试判断这两个三角形是否相似,并说明理由.
解:相似.
理由如下:
∵ = = ,
AC
20
5
AE
12
3
= = ,
AB
25
5
AD
15
3
= = ,
BC
40
5
DE
24
3
∴△ABC∽△ADE.
∴ = = ,
AC
AE
AB
AD
BC
DE
5.如图,已知AD·AC=AB·AE.
(1)求证:△ADE∽△ABC;
∴△ADE∽△ABC.
证明:∵AD·AC=AB·AE,
在△ADE与△ABC 中,
∴ = .
AD
AE
AB
AC
∵ = ,
AD
AE
AB
AC
∠A=∠A,
5.如图,已知AD·AC=AB·AE.
(2)若∠A=45°,∠C=95°,求∠ADE的度数.
∴∠ADE=40°.
解:∵△ADE∽△ABC,
∴∠ADE=∠B.
∵∠A=45°,∠C=95°,
∴∠B=180°-∠A-∠C
=40°,
课堂小结
相似三角形的判定
判定定理1
判定定理2
三边成比例的两个三角形相似.
两边成比例且夹角相等的两个三角形相似.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
