27.2.2相似三角形的性质 同步课件
图片预览






文档简介
(共28张PPT)
课程讲授
新知导入
随堂练习
课堂小结
27.2.2 相似三角形的性质
第二十七章 相似
27.2 相似三角形
知识要点
1.相似三角形对应线段的比等于相似比
2.相似三角形的周长的比等于相似比
3.相似三角形的面积的比等于相似比的平方
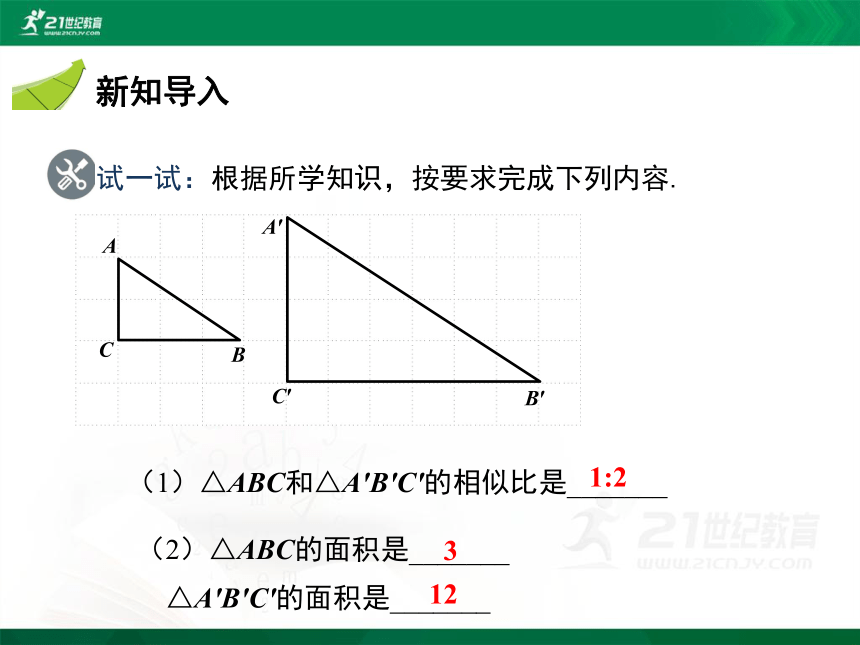
新知导入
试一试:根据所学知识,按要求完成下列内容.
B′
A′
C′
C
A
B
(1)△ABC和△A′B′C′的相似比是_______
(2)△ABC的面积是_______
△A′B′C′的面积是_______
1:2
3
12
课程讲授
1
相似三角形对应线段的比等于相似比
问题1:如图,△ABC ∽△A′B′C′,相似比为k,它们对应高的比是多少?试着证明你的结论.
B
A
C
C′
A′
B′
如图,分别作出 △ABC 和 △A' B' C' 的高 AD 和 A' D' .
D
D'
△ABC 和 △A' B' C' 对应高的比是k
1
相似三角形对应线段的比等于相似比
已知:如图,△ABC和△A'B'C'中,△ABC ∽△A′B′C′, 相似比为k,AD 和 A' D'是 △ABC 和 △A' B' C' 的高.
求证:AD 和 A' D'的比是k.
B
A
C
D
C′
A′
B′
D'
证明:∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
又∵△ABD和△A'B'D'都是直角三角形。
∴△ABD ∽△A'B'D',
∴ = =k
A' D'
AD
AB
A'B'
1
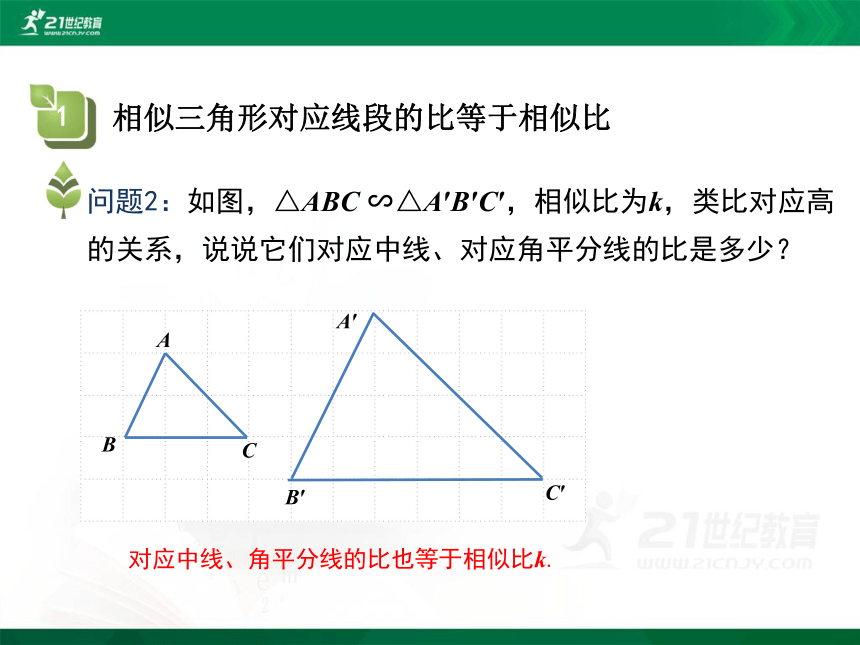
相似三角形对应线段的比等于相似比
问题2:如图,△ABC ∽△A′B′C′,相似比为k,类比对应高的关系,说说它们对应中线、对应角平分线的比是多少?
B
A
C
C′
A′
B′
对应中线、角平分线的比也等于相似比k.
1
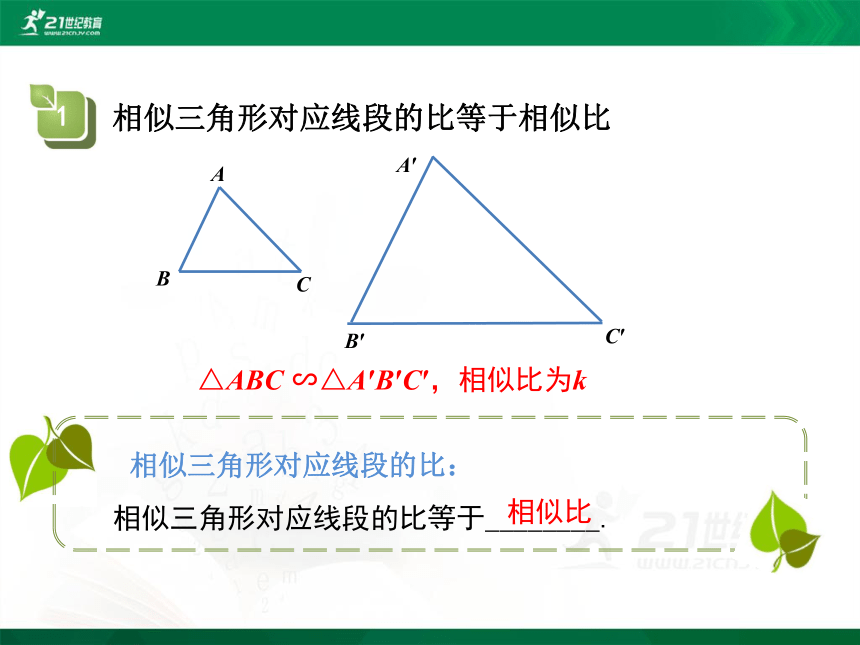
相似三角形对应线段的比等于相似比
相似三角形对应线段的比:
相似三角形对应线段的比等于________.
B
A
C
C′
A′
B′
△ABC ∽△A′B′C′,相似比为k
相似比
1
相似三角形对应线段的比等于相似比
练一练:若△ABC∽△DEF,相似比为3∶2,则对应角平分线的比为( )
A.3∶2
B.3∶5
C.9∶4
D.4∶9
A
2
相似三角形的周长的比等于相似比
问题1:根据相似三角形的特点和已经学习的知识,想一想相似三角形的周长比是多少?
B
A
C
C′
A′
B′
相似三角形的周长比等于相似比k.
2
相似三角形的周长的比等于相似比
问题2:根据所学知识,试着证明你的猜想.
已知:如图,△ABC和△A'B'C'中,△ABC ∽△A′B′C′, 相似比为k.
求证:△ABC和△A'B'C'的周长比是k.
B
A
C
C′
A′
B′
证明:∵△ABC ∽△A′B′C′, 相似比为k,
B'C'
AB
A'B'
BC
=
=
C'A'
CA
= k
∴AB=k A'B',BC=kB'C',CA=kC'A',
∴
∴
AB+BC +CA
A'B'+B'C'+C'A'
=
kA'B'+kB'C'+kC'A'
A'B'+B'C'+C'A'
= k
2
相似三角形的周长的比等于相似比
相似三角形周长的比:
相似三角形周长的比等于________.
B
A
C
C′
A′
B′
△ABC ∽△A′B′C′,相似比为k
相似比
2
相似三角形的周长的比等于相似比
练一练:若△ABC∽△A′B′C′,且 ,△ABC的周长为15 cm,则△A′B′C′的周长为( )
A.18 cm
B.20 cm
C. cm
D. cm
B
3
相似三角形的面积的比等于相似比的平方
问题1:我们已经知道相似三角形对应的高等于相似比,那么相似三角形的面积比等于多少?
B
A
C
C′
A′
B′
D
D'
3
12
3
相似三角形的面积的比等于相似比的平方
由前面的结论,我们有
B
A
C
D
C′
A′
B′
D'
S△ABC
S△A'B'C'
=
2
1
2
1
BC ·AD
B'C' ·A'D'
B'C'
BC
=
A'D'
AD
=k·k
=k2
3
相似三角形的面积的比等于相似比的平方
B
A
C
D
C′
A′
B′
D'
△ABC ∽△A′B′C′,相似比为k
相似三角形面积的比:
相似三角形面积的比等于____________.
相似比的平方
3
相似三角形的面积的比等于相似比的平方
例 如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
E
D
F
C
A
B
3
相似三角形的面积的比等于相似比的平方
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
∴
AB
DE
=
AC
DF
=
2
1
又∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
2
1
面积为( )2× =
2
1
3
相似三角形的面积的比等于相似比的平方
练一练:已知△ABC与△A1B1C1相似,且相似比为1∶3,则△ABC与△A1B1C1的面积比为( )
A.1∶1
B.1∶3
C.1∶6
D.1∶9
D
随堂练习
1.将一个三角形改成与它相似的三角形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
A.9倍
B.3倍
C.81倍
D.18倍
B
2.两个相似三角形的最短边长分别为5 cm和3 cm,它们的周长之差为12 cm,那么大三角形的周长为( )
A.14 cm
B.16 cm
C.18 cm
D.30 cm
D
3.如图,在平行四边形ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
A.
B.
C.
D.
D
4.已知△ABC∽△A′B′C′,CD是AB边上的中线,C′D′是A′B′边上的中线,CD=4 cm,C′D′=10 cm,AE是△ABC的一条高,AE=4.8 cm,求△A′B′C′中对应高A′E′的长.
解:∵△ABC∽△A′B′C′,CD是AB边上的中线,C′D′是A′B′边上的中线,且AE,A′E′是对应的高线,
∴A′E′=12 cm.
= ,
∴
AE
CD
A′E′
C′D′
10
即
4.8
4
= ,
A′E′
5.已知△ABC∽△DEF,△ABC和△DEF的周长分别为20 cm和25 cm,且BC=5 cm,DF=4 cm,求EF和AC的长.
解:∵相似三角形周长的比等于相似比,
∴ = ,
EF
25
BC
20
∴EF= ×BC= ×5= (cm).
4
5
4
5
4
25
同理可得
= ,
EF
20
25
DF
∴EF= ×DF= ×4= (cm).
5
4
5
4
5
16
6.如图,在平行四边形ABCD中,AE∶EB=1∶2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6 cm2,求S△CDF的值.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△CDF∽△AEF.
∵AE∶EB=1∶2,
∴AE∶AB=1∶3,
∴AE∶CD=1∶3,
∴△AEF与△CDF的周长比为1∶3.
∴S△CDF=9S△AEF=54 cm2.
6.如图,在平行四边形ABCD中,AE∶EB=1∶2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6 cm2,求S△CDF的值.
解:(2)∵△CDF∽△AEF,AE∶CD=1∶3,
∴S△AEF∶S△CDF=1∶9,
课堂小结
相似三角形的性质
对应线段的比
相似三角形对应线段的比等于相似比.
周长的比
相似三角形周长的比等于相似比.
面积的比
相似三角形面积的比等于相似比的平方.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
课程讲授
新知导入
随堂练习
课堂小结
27.2.2 相似三角形的性质
第二十七章 相似
27.2 相似三角形
知识要点
1.相似三角形对应线段的比等于相似比
2.相似三角形的周长的比等于相似比
3.相似三角形的面积的比等于相似比的平方
新知导入
试一试:根据所学知识,按要求完成下列内容.
B′
A′
C′
C
A
B
(1)△ABC和△A′B′C′的相似比是_______
(2)△ABC的面积是_______
△A′B′C′的面积是_______
1:2
3
12
课程讲授
1
相似三角形对应线段的比等于相似比
问题1:如图,△ABC ∽△A′B′C′,相似比为k,它们对应高的比是多少?试着证明你的结论.
B
A
C
C′
A′
B′
如图,分别作出 △ABC 和 △A' B' C' 的高 AD 和 A' D' .
D
D'
△ABC 和 △A' B' C' 对应高的比是k
1
相似三角形对应线段的比等于相似比
已知:如图,△ABC和△A'B'C'中,△ABC ∽△A′B′C′, 相似比为k,AD 和 A' D'是 △ABC 和 △A' B' C' 的高.
求证:AD 和 A' D'的比是k.
B
A
C
D
C′
A′
B′
D'
证明:∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
又∵△ABD和△A'B'D'都是直角三角形。
∴△ABD ∽△A'B'D',
∴ = =k
A' D'
AD
AB
A'B'
1
相似三角形对应线段的比等于相似比
问题2:如图,△ABC ∽△A′B′C′,相似比为k,类比对应高的关系,说说它们对应中线、对应角平分线的比是多少?
B
A
C
C′
A′
B′
对应中线、角平分线的比也等于相似比k.
1
相似三角形对应线段的比等于相似比
相似三角形对应线段的比:
相似三角形对应线段的比等于________.
B
A
C
C′
A′
B′
△ABC ∽△A′B′C′,相似比为k
相似比
1
相似三角形对应线段的比等于相似比
练一练:若△ABC∽△DEF,相似比为3∶2,则对应角平分线的比为( )
A.3∶2
B.3∶5
C.9∶4
D.4∶9
A
2
相似三角形的周长的比等于相似比
问题1:根据相似三角形的特点和已经学习的知识,想一想相似三角形的周长比是多少?
B
A
C
C′
A′
B′
相似三角形的周长比等于相似比k.
2
相似三角形的周长的比等于相似比
问题2:根据所学知识,试着证明你的猜想.
已知:如图,△ABC和△A'B'C'中,△ABC ∽△A′B′C′, 相似比为k.
求证:△ABC和△A'B'C'的周长比是k.
B
A
C
C′
A′
B′
证明:∵△ABC ∽△A′B′C′, 相似比为k,
B'C'
AB
A'B'
BC
=
=
C'A'
CA
= k
∴AB=k A'B',BC=kB'C',CA=kC'A',
∴
∴
AB+BC +CA
A'B'+B'C'+C'A'
=
kA'B'+kB'C'+kC'A'
A'B'+B'C'+C'A'
= k
2
相似三角形的周长的比等于相似比
相似三角形周长的比:
相似三角形周长的比等于________.
B
A
C
C′
A′
B′
△ABC ∽△A′B′C′,相似比为k
相似比
2
相似三角形的周长的比等于相似比
练一练:若△ABC∽△A′B′C′,且 ,△ABC的周长为15 cm,则△A′B′C′的周长为( )
A.18 cm
B.20 cm
C. cm
D. cm
B
3
相似三角形的面积的比等于相似比的平方
问题1:我们已经知道相似三角形对应的高等于相似比,那么相似三角形的面积比等于多少?
B
A
C
C′
A′
B′
D
D'
3
12
3
相似三角形的面积的比等于相似比的平方
由前面的结论,我们有
B
A
C
D
C′
A′
B′
D'
S△ABC
S△A'B'C'
=
2
1
2
1
BC ·AD
B'C' ·A'D'
B'C'
BC
=
A'D'
AD
=k·k
=k2
3
相似三角形的面积的比等于相似比的平方
B
A
C
D
C′
A′
B′
D'
△ABC ∽△A′B′C′,相似比为k
相似三角形面积的比:
相似三角形面积的比等于____________.
相似比的平方
3
相似三角形的面积的比等于相似比的平方
例 如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
E
D
F
C
A
B
3
相似三角形的面积的比等于相似比的平方
解:在 △ABC 和 △DEF 中,
∵ AB=2DE,AC=2DF,
∴
AB
DE
=
AC
DF
=
2
1
又∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
2
1
面积为( )2× =
2
1
3
相似三角形的面积的比等于相似比的平方
练一练:已知△ABC与△A1B1C1相似,且相似比为1∶3,则△ABC与△A1B1C1的面积比为( )
A.1∶1
B.1∶3
C.1∶6
D.1∶9
D
随堂练习
1.将一个三角形改成与它相似的三角形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )
A.9倍
B.3倍
C.81倍
D.18倍
B
2.两个相似三角形的最短边长分别为5 cm和3 cm,它们的周长之差为12 cm,那么大三角形的周长为( )
A.14 cm
B.16 cm
C.18 cm
D.30 cm
D
3.如图,在平行四边形ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
A.
B.
C.
D.
D
4.已知△ABC∽△A′B′C′,CD是AB边上的中线,C′D′是A′B′边上的中线,CD=4 cm,C′D′=10 cm,AE是△ABC的一条高,AE=4.8 cm,求△A′B′C′中对应高A′E′的长.
解:∵△ABC∽△A′B′C′,CD是AB边上的中线,C′D′是A′B′边上的中线,且AE,A′E′是对应的高线,
∴A′E′=12 cm.
= ,
∴
AE
CD
A′E′
C′D′
10
即
4.8
4
= ,
A′E′
5.已知△ABC∽△DEF,△ABC和△DEF的周长分别为20 cm和25 cm,且BC=5 cm,DF=4 cm,求EF和AC的长.
解:∵相似三角形周长的比等于相似比,
∴ = ,
EF
25
BC
20
∴EF= ×BC= ×5= (cm).
4
5
4
5
4
25
同理可得
= ,
EF
20
25
DF
∴EF= ×DF= ×4= (cm).
5
4
5
4
5
16
6.如图,在平行四边形ABCD中,AE∶EB=1∶2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6 cm2,求S△CDF的值.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△CDF∽△AEF.
∵AE∶EB=1∶2,
∴AE∶AB=1∶3,
∴AE∶CD=1∶3,
∴△AEF与△CDF的周长比为1∶3.
∴S△CDF=9S△AEF=54 cm2.
6.如图,在平行四边形ABCD中,AE∶EB=1∶2.
(1)求△AEF与△CDF的周长比;
(2)如果S△AEF=6 cm2,求S△CDF的值.
解:(2)∵△CDF∽△AEF,AE∶CD=1∶3,
∴S△AEF∶S△CDF=1∶9,
课堂小结
相似三角形的性质
对应线段的比
相似三角形对应线段的比等于相似比.
周长的比
相似三角形周长的比等于相似比.
面积的比
相似三角形面积的比等于相似比的平方.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
