27.2.3相似三角形应用举例 同步课件
图片预览






文档简介
(共24张PPT)
课程讲授
新知导入
随堂练习
课堂小结
27.2.3 相似三角形应用举例
第二十七章 相似
27.2 相似三角形
知识要点
1.测量物高
2.测量距离
新知导入
看一看:观察下图中的建筑,想一想人们如何测量出它们的实际高度。
上海中心大厦建筑主体为119层,总高为632米,结构高度为580米
新知导入
哈利法塔高828米,楼层总数162层
看一看:观察下图中的建筑,想一想人们如何测量出它们的实际高度。
课程讲授
1
测量物高
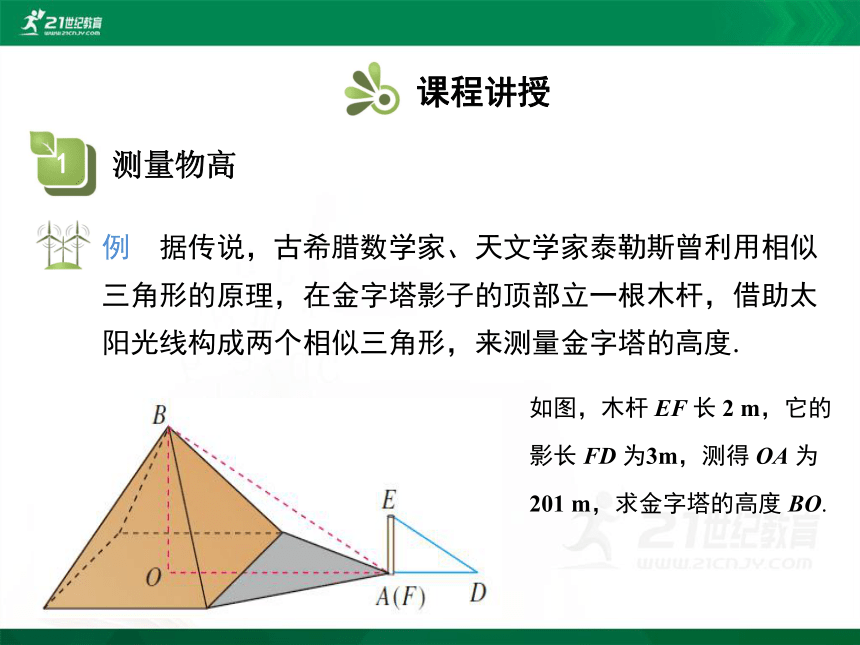
例 据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,木杆 EF 长 2 m,它的影长 FD 为3m,测得 OA 为 201 m,求金字塔的高度 BO.
1
测量物高
解:太阳光是平行的光线,因此
∠BAO =∠EDF.
又 ∠AOB =∠DFE = 90°,
∴△ABO ∽△DEF.
∴ = ,
BO
OA
EF
FD
∴ = = =134 (m).
BO
OA·EF
FD
201×2
3
因此金字塔的高度为134 m.
1
测量物高
归纳:测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
物1高 :物2高 = 影1长 :影2长
1
测量物高
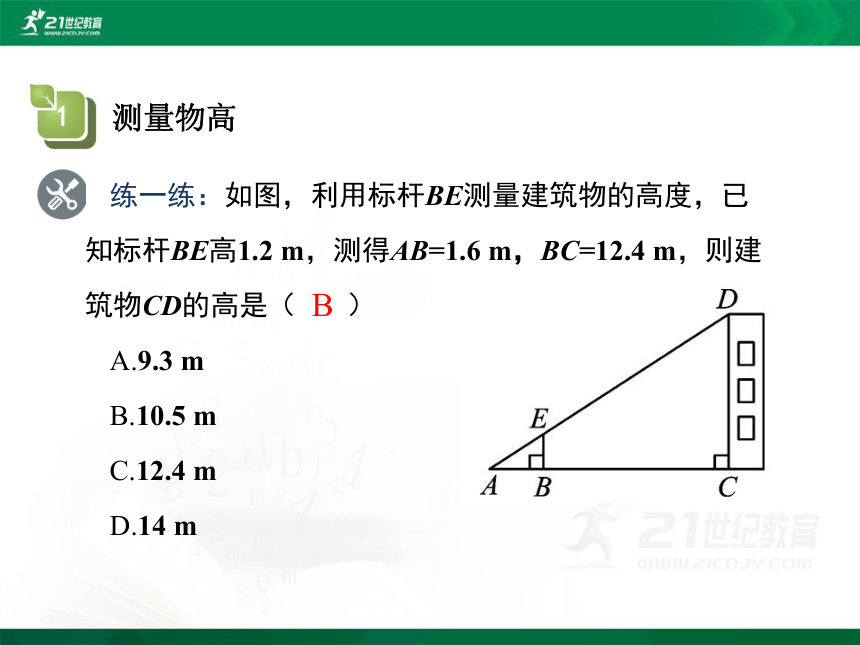
练一练:如图,利用标杆BE测量建筑物的高度,已知标杆BE高1.2 m,测得AB=1.6 m,BC=12.4 m,则建筑物CD的高是( )
A.9.3 m
B.10.5 m
C.12.4 m
D.14 m
B
2
测量距离
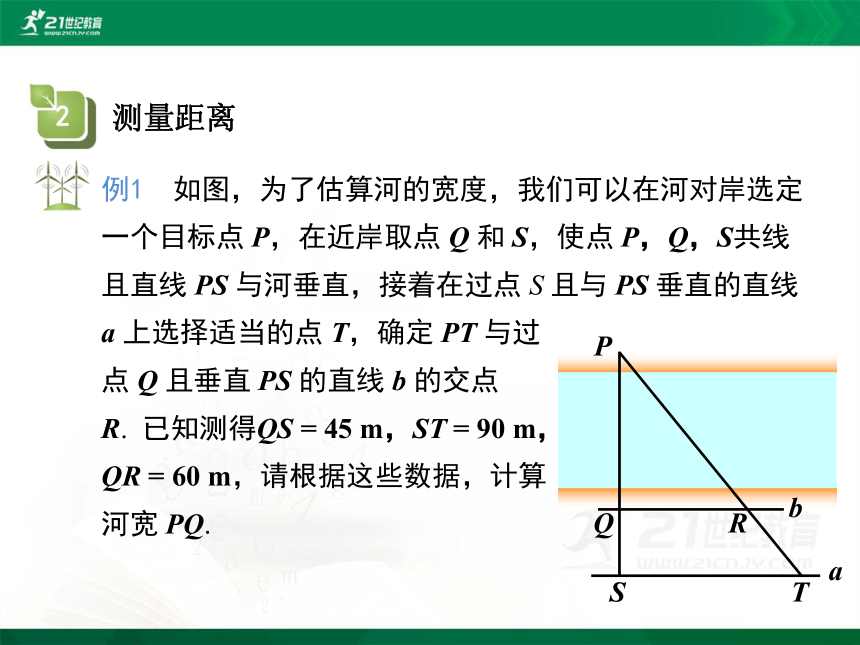
例1 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点 P,在近岸取点 Q 和 S,使点 P,Q,S共线且直线 PS 与河垂直,接着在过点 S 且与 PS 垂直的直线 a 上选择适当的点 T,确定 PT 与过
点 Q 且垂直 PS 的直线 b 的交点
R. 已知测得QS = 45 m,ST = 90 m,
QR = 60 m,请根据这些数据,计算
河宽 PQ.
P
R
Q
S
b
T
a
2
测量距离
P
R
Q
S
b
T
a
解:∵∠PQR =∠PST =90°,∠P=∠P,
∴△PQR∽△PST.
∴ = ,
PQ
QR
PS
ST
即 =
PQ
PQ+QS
QR
ST
=
PQ
PQ+45
60
90
PQ×90 = (PQ+45)×60.
因此,河宽大约为 90 m.
解得 PQ = 90.
2
测量距离
例2 如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了?
2
测量距离
解:如图,假设观察者从左向右走到点 E 时,她的眼睛的位置点 E 与两棵树的顶端点 A,C 恰在一条直线上.
∵AB⊥l,CD⊥l,
∴AB∥CD.
∴△AEH∽△CEK.
∴ = ,
EH
AH
EK
CK
∴ = = ,
EH
8-1.6
EH+5
12-1.6
6.4
10.4
解得 EH=8.
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
2
测量距离
归纳:测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解.
2
测量距离
练一练:如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB∶AP=2∶5,BC=20 cm,则PQ的长是( )
A.45 cm
B.50 cm
C.60 cm
D.80 cm
B
随堂练习
1.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为点B,D.若AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的高度CD为____________m.
0.4
2.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,则河宽AB=_________m.
100
3.墨子是春秋战国时期墨家学派的创始人,著名思想家、教育家、科学家、军事家.墨子曾和他的学生做过小孔成像的实验.他的做法是,在一间黑暗的屋子里,一面墙上开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小华在学习了小孔成像的原理后,利用如图所示的装置来验证小孔成像的现象.已知一根点燃的蜡烛距小孔20 cm,光屏在距小孔30 cm处,小华测量了蜡烛的火焰高度为2 cm,则光屏上火焰所成像的高度为________cm.
3
4.如图是一位同学设计的用手电筒来测量墙面高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=4米,BP=6米,PD=24米,求CD的高度.
∴CD=16米.
解:由题意,得∠APB=∠CPD.
∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,
∴△ABP∽△CDP,
∴ = ,
AB
BP
CD
DP
即 = ,
4
CD
6
24
答:CD的高度为16米.
5.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C,A共线.
已知CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m,测量示意图如图所示.请根据相关测量信息,求河宽AB.
答:河宽AB为17 m.
解:∵CB⊥AD,ED⊥AD,
∴BC∥DE,
∴△ABC∽△ADE,
∴ = ,
BC
AB
DE
AD
∴ = ,
1
AB
1.5
AD+8.5
∴AB=17 m.
课堂小结
相似三角形应用举例
测量物高
测量距离
在同一时刻物高与影长成正比例
测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
课程讲授
新知导入
随堂练习
课堂小结
27.2.3 相似三角形应用举例
第二十七章 相似
27.2 相似三角形
知识要点
1.测量物高
2.测量距离
新知导入
看一看:观察下图中的建筑,想一想人们如何测量出它们的实际高度。
上海中心大厦建筑主体为119层,总高为632米,结构高度为580米
新知导入
哈利法塔高828米,楼层总数162层
看一看:观察下图中的建筑,想一想人们如何测量出它们的实际高度。
课程讲授
1
测量物高
例 据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,木杆 EF 长 2 m,它的影长 FD 为3m,测得 OA 为 201 m,求金字塔的高度 BO.
1
测量物高
解:太阳光是平行的光线,因此
∠BAO =∠EDF.
又 ∠AOB =∠DFE = 90°,
∴△ABO ∽△DEF.
∴ = ,
BO
OA
EF
FD
∴ = = =134 (m).
BO
OA·EF
FD
201×2
3
因此金字塔的高度为134 m.
1
测量物高
归纳:测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
物1高 :物2高 = 影1长 :影2长
1
测量物高
练一练:如图,利用标杆BE测量建筑物的高度,已知标杆BE高1.2 m,测得AB=1.6 m,BC=12.4 m,则建筑物CD的高是( )
A.9.3 m
B.10.5 m
C.12.4 m
D.14 m
B
2
测量距离
例1 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点 P,在近岸取点 Q 和 S,使点 P,Q,S共线且直线 PS 与河垂直,接着在过点 S 且与 PS 垂直的直线 a 上选择适当的点 T,确定 PT 与过
点 Q 且垂直 PS 的直线 b 的交点
R. 已知测得QS = 45 m,ST = 90 m,
QR = 60 m,请根据这些数据,计算
河宽 PQ.
P
R
Q
S
b
T
a
2
测量距离
P
R
Q
S
b
T
a
解:∵∠PQR =∠PST =90°,∠P=∠P,
∴△PQR∽△PST.
∴ = ,
PQ
QR
PS
ST
即 =
PQ
PQ+QS
QR
ST
=
PQ
PQ+45
60
90
PQ×90 = (PQ+45)×60.
因此,河宽大约为 90 m.
解得 PQ = 90.
2
测量距离
例2 如图,左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m,两树底部的距离 BD = 5 m,一个人估计自己眼睛距离地面 1.6 m,她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就看不到右边较高的树的顶端C 了?
2
测量距离
解:如图,假设观察者从左向右走到点 E 时,她的眼睛的位置点 E 与两棵树的顶端点 A,C 恰在一条直线上.
∵AB⊥l,CD⊥l,
∴AB∥CD.
∴△AEH∽△CEK.
∴ = ,
EH
AH
EK
CK
∴ = = ,
EH
8-1.6
EH+5
12-1.6
6.4
10.4
解得 EH=8.
由此可知,如果观察者继续前进,当她与左边的树的距离小于 8 m 时,由于这棵树的遮挡,就看不到右边树的顶端 C .
2
测量距离
归纳:测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解.
2
测量距离
练一练:如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB∶AP=2∶5,BC=20 cm,则PQ的长是( )
A.45 cm
B.50 cm
C.60 cm
D.80 cm
B
随堂练习
1.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为点B,D.若AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的高度CD为____________m.
0.4
2.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,则河宽AB=_________m.
100
3.墨子是春秋战国时期墨家学派的创始人,著名思想家、教育家、科学家、军事家.墨子曾和他的学生做过小孔成像的实验.他的做法是,在一间黑暗的屋子里,一面墙上开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小华在学习了小孔成像的原理后,利用如图所示的装置来验证小孔成像的现象.已知一根点燃的蜡烛距小孔20 cm,光屏在距小孔30 cm处,小华测量了蜡烛的火焰高度为2 cm,则光屏上火焰所成像的高度为________cm.
3
4.如图是一位同学设计的用手电筒来测量墙面高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到CD的顶端C处.已知AB⊥BD,CD⊥BD,测得AB=4米,BP=6米,PD=24米,求CD的高度.
∴CD=16米.
解:由题意,得∠APB=∠CPD.
∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,
∴△ABP∽△CDP,
∴ = ,
AB
BP
CD
DP
即 = ,
4
CD
6
24
答:CD的高度为16米.
5.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C,A共线.
已知CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m,测量示意图如图所示.请根据相关测量信息,求河宽AB.
答:河宽AB为17 m.
解:∵CB⊥AD,ED⊥AD,
∴BC∥DE,
∴△ABC∽△ADE,
∴ = ,
BC
AB
DE
AD
∴ = ,
1
AB
1.5
AD+8.5
∴AB=17 m.
课堂小结
相似三角形应用举例
测量物高
测量距离
在同一时刻物高与影长成正比例
测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
