27.3位似(用坐标表示位似)第2课时 课件
文档属性
| 名称 | 27.3位似(用坐标表示位似)第2课时 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 15:31:24 | ||
图片预览




文档简介
(共20张PPT)
27.3 位似
第二十七章 相似
课程讲授
新知导入
随堂练习
课堂小结
第2课时 用坐标表示位似
知识要点
1.位似图形的坐标变化规律
2.在坐标系中作位似图形
新知导入
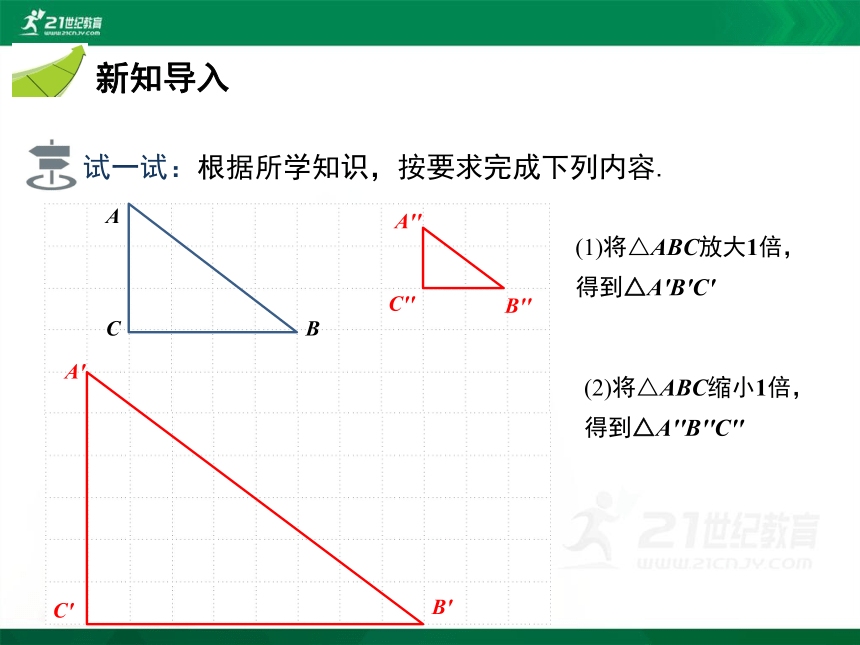
试一试:根据所学知识,按要求完成下列内容.
C
A
B
(1)将△ABC放大1倍,得到△A'B'C'
(2)将△ABC缩小1倍,得到△A''B''C''
C''
A''
B''
C'
A'
B'
课程讲授
1
位似图形的坐标变化规律
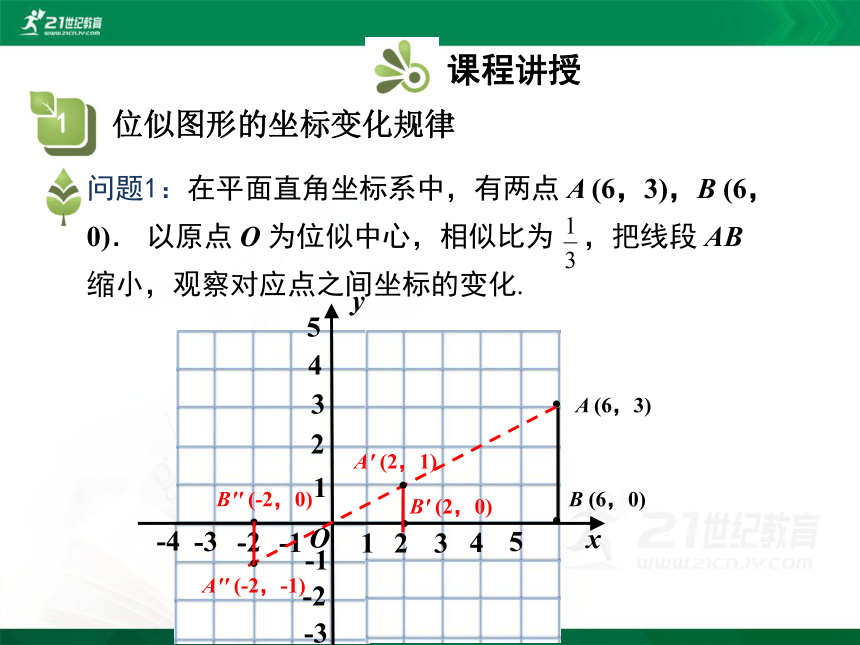
问题1:在平面直角坐标系中,有两点 A (6,3),B (6,0). 以原点 O 为位似中心,相似比为 ,把线段 AB 缩小,观察对应点之间坐标的变化.
-1
-2
-3
-4
5
1
-2
3
-1
2
-3
4
1
2
3
4
5
y
O
x
A (6,3)
B (6,0)
A' (2,1)
B' (2,0)
A'' (-2,-1)
B'' (-2,0)
1
位似图形的坐标变化规律
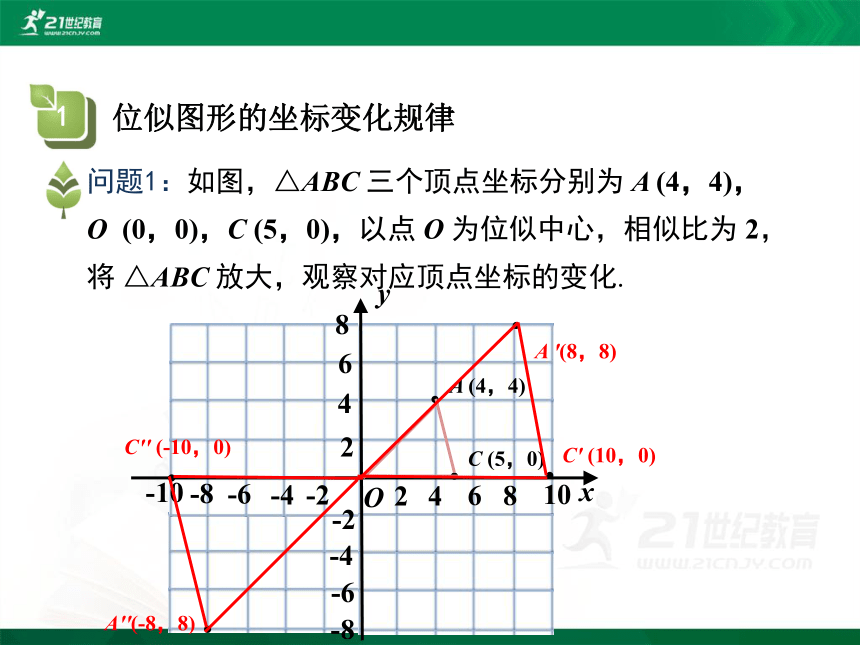
问题1:如图,△ABC 三个顶点坐标分别为 A (4,4),O (0,0),C (5,0),以点 O 为位似中心,相似比为 2,将 △ABC 放大,观察对应顶点坐标的变化.
-2
-4
-6
-8
-8
2
-4
6
-2
4
-6
8
-10
2
4
6
8
10
y
O
x
A (4,4)
C (5,0)
A '(8,8)
C' (10,0)
A''(-8,8)
C'' (-10,0)
1
位似图形的坐标变化规律
归纳:在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
1
位似图形的坐标变化规律
位似图形的坐标变化规律:
一般地,在平面直角坐标系中,画一个与原图形位似的图形,使它和原图形的相似比为k,那么原图形上的点(x,y),对应位似图形上的点的坐标为_______或__________.
(kx,ky)
(-kx,-ky)
1
位似图形的坐标变化规律
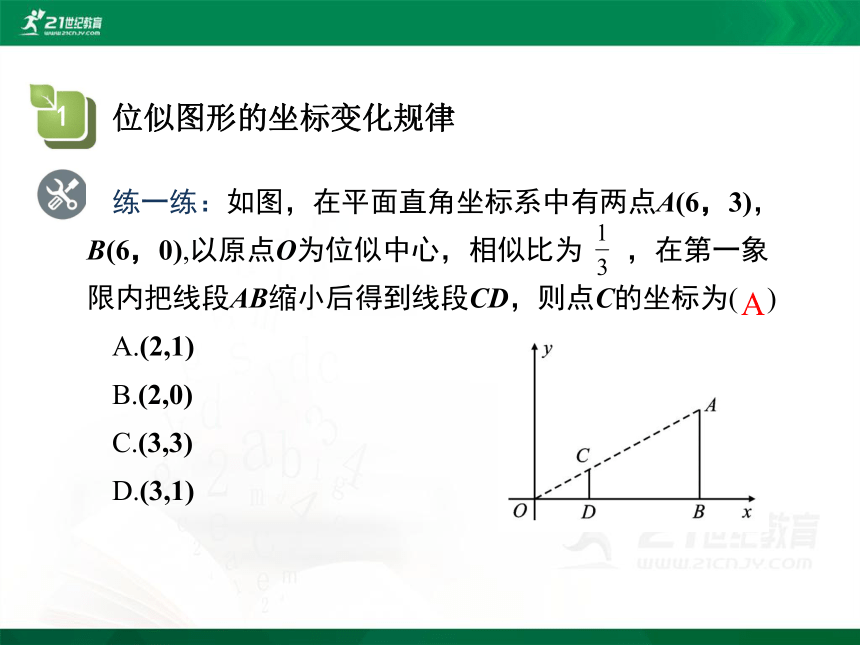
练一练:如图,在平面直角坐标系中有两点A(6,3),B(6,0),以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(2,0)
C.(3,3)
D.(3,1)
A
2
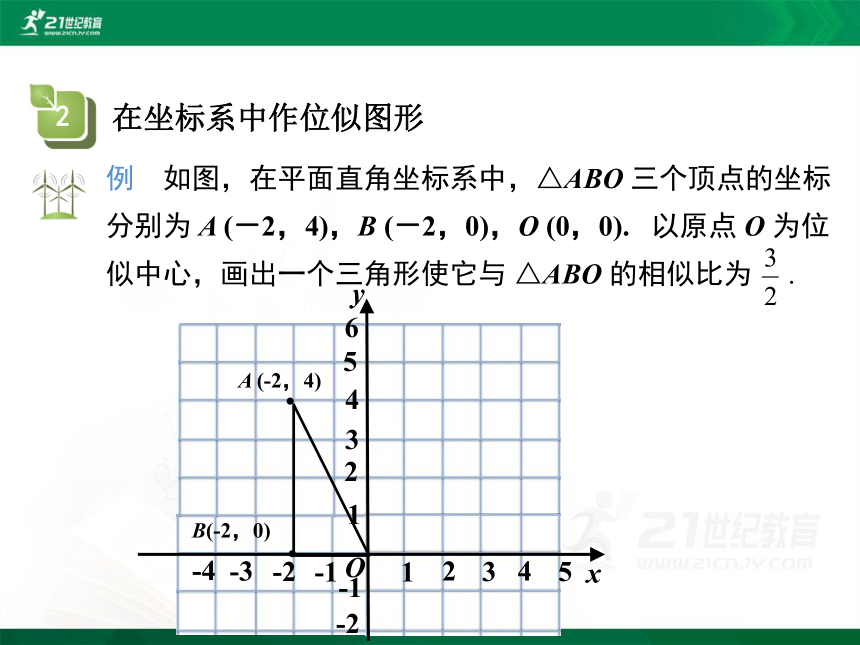
在坐标系中作位似图形
例 如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 .
-1
-2
-3
-4
5
1
-2
3
-1
2
6
4
1
2
3
4
5
y
O
x
A (-2,4)
B(-2,0)
2
在坐标系中作位似图形
-1
-2
-3
-4
5
1
-2
3
-1
2
6
4
1
2
3
4
5
y
O
x
A (-2,4)
B(-2,0)
解:利用位似中对应点的坐标的变化规律,分别取点 A′ (-3,6),B′ (-3,0),O (0,0).
A' (-3,6)
B' (-3,0)
顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
2
在坐标系中作位似图形
练一练:如图,在直角坐标系中,作出五边形ABCDE的位似图形,使得新图形A1B1C1D1E1与原图形对应线段比为2∶1,位似中心是坐标原点O.
E1
A1
B1
C1
D1
随堂练习
1.如图,在平面直角坐标中,以原点为位似中心,将△AOB扩大到原来的2倍,得到△OA′B′,若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4)
B.(-1,-2)
C.(-2,-4)
D.(-2,-1)
C
2.如图,在直角坐标系中,矩形OABC的顶点 O在坐标原点,边 OA在 x轴上,边OC在 y轴上.如果矩形OA′B′C′与矩形OABC关于点 O位似,且矩形OA′B′C′与矩形OABC的相似比为1:2,那么点 B′的坐标是( )
A.(-2,3)
B.(2,-3)
C.(3,-2)或(-2,3)
D.(-2,3)或(2,-3)
D
3.如图,△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2),以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且相似比为2∶1,点C1的坐标是( )
A.(1,0)
B.(1,1)
C.(-3,2)
D.(0,0)
A
4.如图,正方形OABC与正方形ODEF是位似图形,点O是位似中心,相似比为1∶ .若点D的坐标为(0,2 ),则点B的坐标是___________.
(2,2)
5.如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B和点B′的坐标分别为B(3,1),B′(6,2).
(1)请你根据位似的特征并结合点B的坐标变化回答下列问题:
①若点A的坐标为(2.5,3),则
点A′的坐标为_________;
②△ABC与△A′B′C′的相似比
为________;
(5,6)
1:2
(2)若△ABC的面积为m,求△A′B′C′的面积.(用含m的代数式表示)
∴△A′B′C′的面积为4m.
解:∵△ABC与△A′B′C′的相似比为1∶2,
∴S△ABC:S△A′B′C′=1:4.
∵△ABC的面积为m,
课堂小结
在坐标系中作位似图形
用坐标表示位似
位似图形的坐标变化规律
一般地,在平面直角坐标系中,画一个与原图形位似的图形,使它和原图形的相似比为k,那么原图形上的点(x,y),对应位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
(3)顺次连接上述各点,得到放大或缩小的图形.
(1)根据相似比,计算对应点的坐标;
(2)分别在坐标系中画出上述对应点;
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
27.3 位似
第二十七章 相似
课程讲授
新知导入
随堂练习
课堂小结
第2课时 用坐标表示位似
知识要点
1.位似图形的坐标变化规律
2.在坐标系中作位似图形
新知导入
试一试:根据所学知识,按要求完成下列内容.
C
A
B
(1)将△ABC放大1倍,得到△A'B'C'
(2)将△ABC缩小1倍,得到△A''B''C''
C''
A''
B''
C'
A'
B'
课程讲授
1
位似图形的坐标变化规律
问题1:在平面直角坐标系中,有两点 A (6,3),B (6,0). 以原点 O 为位似中心,相似比为 ,把线段 AB 缩小,观察对应点之间坐标的变化.
-1
-2
-3
-4
5
1
-2
3
-1
2
-3
4
1
2
3
4
5
y
O
x
A (6,3)
B (6,0)
A' (2,1)
B' (2,0)
A'' (-2,-1)
B'' (-2,0)
1
位似图形的坐标变化规律
问题1:如图,△ABC 三个顶点坐标分别为 A (4,4),O (0,0),C (5,0),以点 O 为位似中心,相似比为 2,将 △ABC 放大,观察对应顶点坐标的变化.
-2
-4
-6
-8
-8
2
-4
6
-2
4
-6
8
-10
2
4
6
8
10
y
O
x
A (4,4)
C (5,0)
A '(8,8)
C' (10,0)
A''(-8,8)
C'' (-10,0)
1
位似图形的坐标变化规律
归纳:在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
1
位似图形的坐标变化规律
位似图形的坐标变化规律:
一般地,在平面直角坐标系中,画一个与原图形位似的图形,使它和原图形的相似比为k,那么原图形上的点(x,y),对应位似图形上的点的坐标为_______或__________.
(kx,ky)
(-kx,-ky)
1
位似图形的坐标变化规律
练一练:如图,在平面直角坐标系中有两点A(6,3),B(6,0),以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1)
B.(2,0)
C.(3,3)
D.(3,1)
A
2
在坐标系中作位似图形
例 如图,在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形使它与 △ABO 的相似比为 .
-1
-2
-3
-4
5
1
-2
3
-1
2
6
4
1
2
3
4
5
y
O
x
A (-2,4)
B(-2,0)
2
在坐标系中作位似图形
-1
-2
-3
-4
5
1
-2
3
-1
2
6
4
1
2
3
4
5
y
O
x
A (-2,4)
B(-2,0)
解:利用位似中对应点的坐标的变化规律,分别取点 A′ (-3,6),B′ (-3,0),O (0,0).
A' (-3,6)
B' (-3,0)
顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
2
在坐标系中作位似图形
练一练:如图,在直角坐标系中,作出五边形ABCDE的位似图形,使得新图形A1B1C1D1E1与原图形对应线段比为2∶1,位似中心是坐标原点O.
E1
A1
B1
C1
D1
随堂练习
1.如图,在平面直角坐标中,以原点为位似中心,将△AOB扩大到原来的2倍,得到△OA′B′,若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4)
B.(-1,-2)
C.(-2,-4)
D.(-2,-1)
C
2.如图,在直角坐标系中,矩形OABC的顶点 O在坐标原点,边 OA在 x轴上,边OC在 y轴上.如果矩形OA′B′C′与矩形OABC关于点 O位似,且矩形OA′B′C′与矩形OABC的相似比为1:2,那么点 B′的坐标是( )
A.(-2,3)
B.(2,-3)
C.(3,-2)或(-2,3)
D.(-2,3)或(2,-3)
D
3.如图,△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2),以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且相似比为2∶1,点C1的坐标是( )
A.(1,0)
B.(1,1)
C.(-3,2)
D.(0,0)
A
4.如图,正方形OABC与正方形ODEF是位似图形,点O是位似中心,相似比为1∶ .若点D的坐标为(0,2 ),则点B的坐标是___________.
(2,2)
5.如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B和点B′的坐标分别为B(3,1),B′(6,2).
(1)请你根据位似的特征并结合点B的坐标变化回答下列问题:
①若点A的坐标为(2.5,3),则
点A′的坐标为_________;
②△ABC与△A′B′C′的相似比
为________;
(5,6)
1:2
(2)若△ABC的面积为m,求△A′B′C′的面积.(用含m的代数式表示)
∴△A′B′C′的面积为4m.
解:∵△ABC与△A′B′C′的相似比为1∶2,
∴S△ABC:S△A′B′C′=1:4.
∵△ABC的面积为m,
课堂小结
在坐标系中作位似图形
用坐标表示位似
位似图形的坐标变化规律
一般地,在平面直角坐标系中,画一个与原图形位似的图形,使它和原图形的相似比为k,那么原图形上的点(x,y),对应位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
(3)顺次连接上述各点,得到放大或缩小的图形.
(1)根据相似比,计算对应点的坐标;
(2)分别在坐标系中画出上述对应点;
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
