28.1 锐角三角函数(余弦与正切)第2课时 课件
文档属性
| 名称 | 28.1 锐角三角函数(余弦与正切)第2课时 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
28.1 锐角三角函数
第二十八章 锐角三角函数
课程讲授
新知导入
随堂练习
课堂小结
第2课时 余弦与正切
知识要点
1.余弦
2.正切
3.锐角三角函数
新知导入
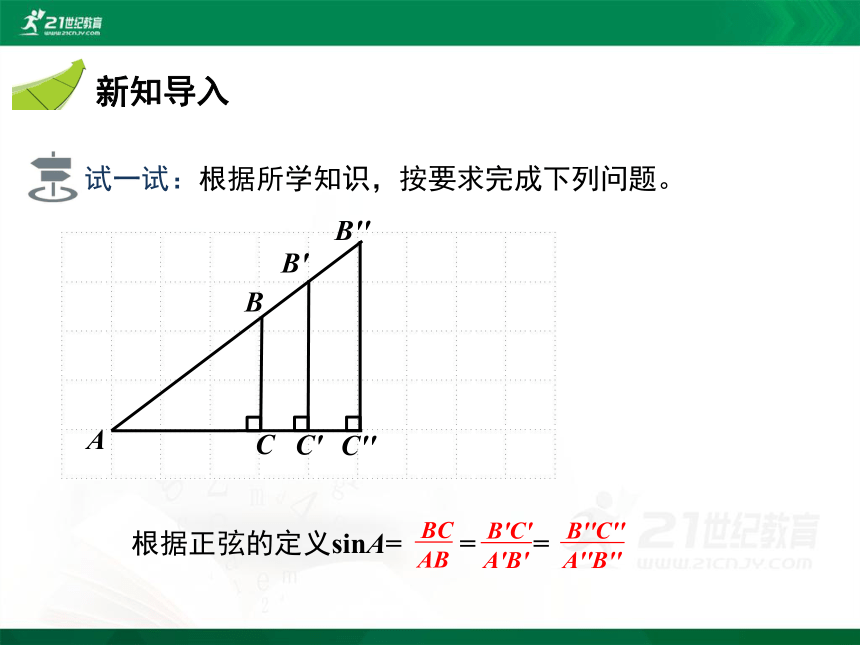
试一试:根据所学知识,按要求完成下列问题。
A
B
C
B'
B''
C'
C''
根据正弦的定义sinA= = =
AB
BC
A'B'
B'C'
A''B''
B''C''
课程讲授
1
余弦
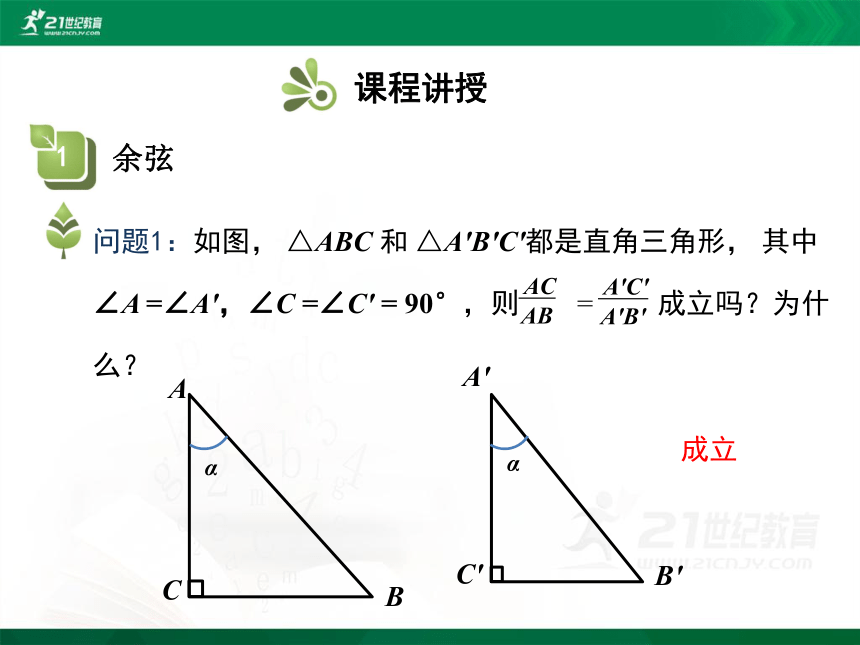
问题1:如图, △ABC 和 △A'B'C'都是直角三角形, 其中∠A =∠A',∠C =∠C' = 90°,则 = 成立吗?为什么?
AB
AC
A'B'
A'C'
A
B
C
α
A'
B'
C'
α
成立
1
余弦
A
B
C
α
A'
B'
C'
α
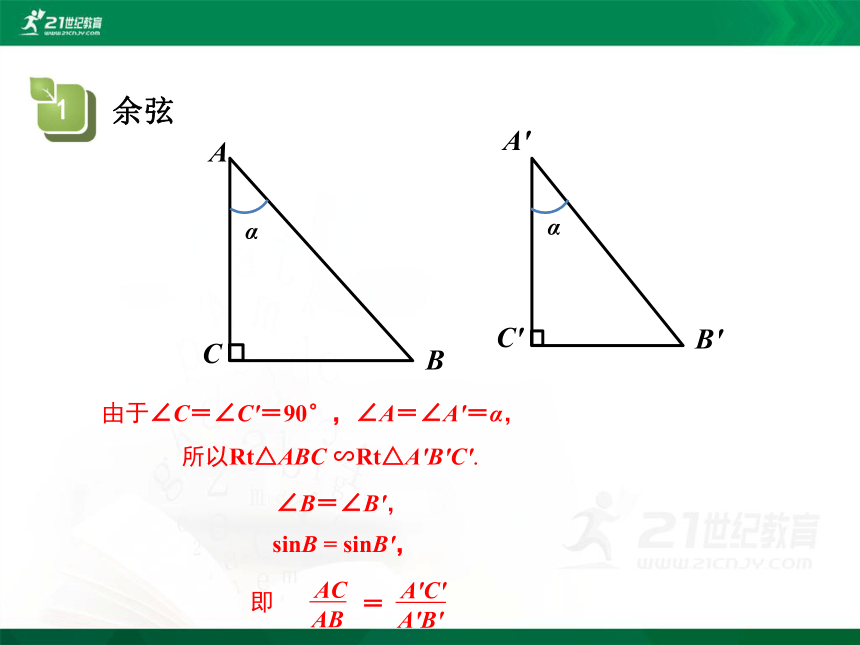
由于∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'.
∠B=∠B',
sinB = sinB',
AB
AC
A'B'
A'C'
=
即
1
余弦
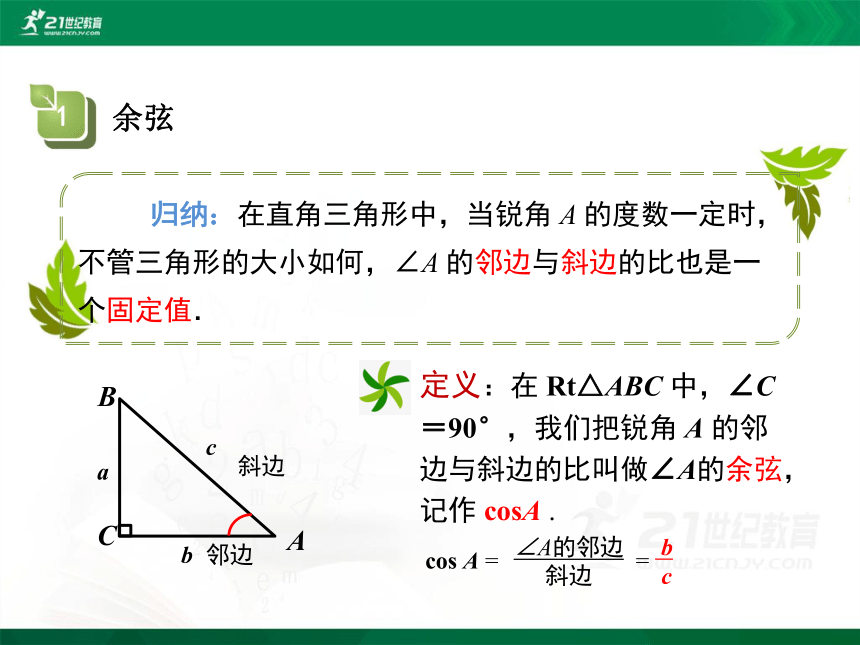
归纳:在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的邻边与斜边的比也是一个固定值.
B
A
C
c
a
b
斜边
邻边
定义:在 Rt△ABC 中,∠C=90°,我们把锐角 A 的邻边与斜边的比叫做∠A的余弦,记作 cosA .
∠A的邻边
斜边
cos A = =
c
b
1
余弦
A
B
C
α
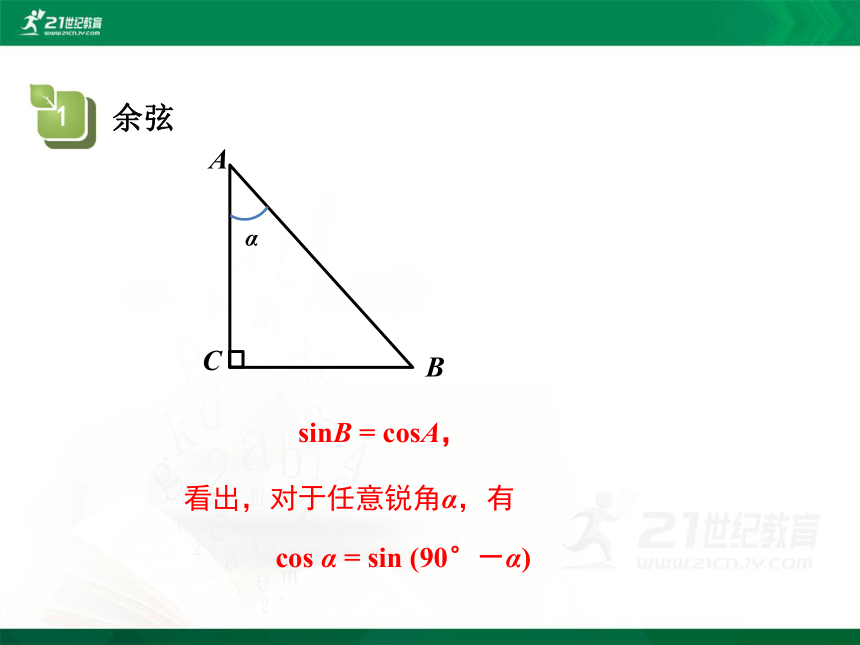
sinB = cosA,
看出,对于任意锐角α,有
cos α = sin (90°-α)
1
余弦
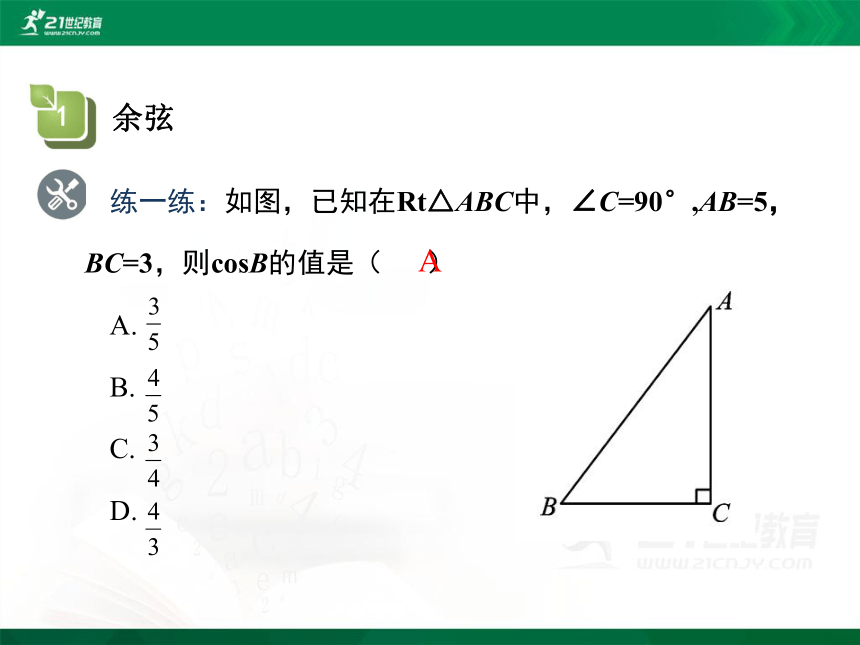
练一练:如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
A.
B.
C.
D.
A
2
正切
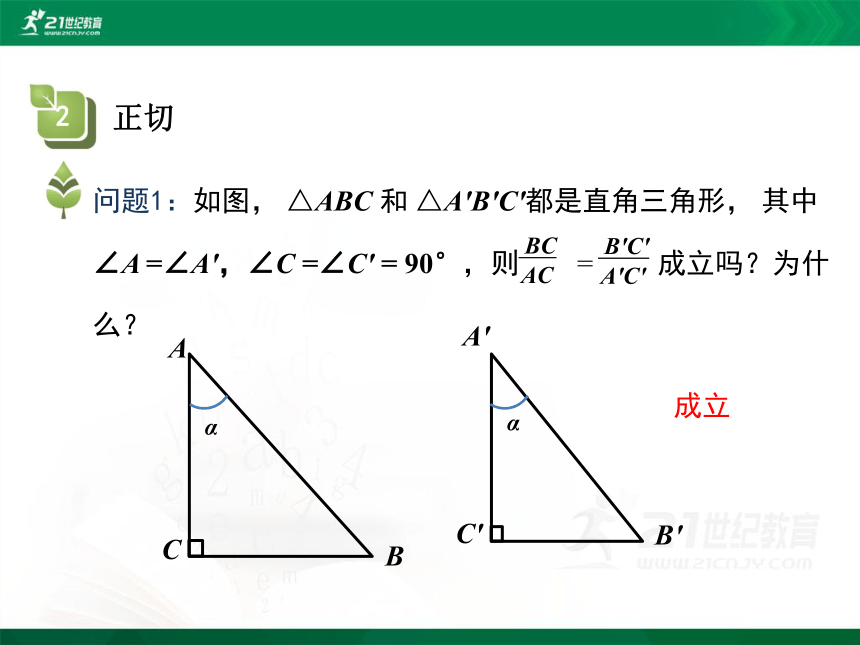
问题1:如图, △ABC 和 △A'B'C'都是直角三角形, 其中∠A =∠A',∠C =∠C' = 90°,则 = 成立吗?为什么?
AC
BC
A'C'
B'C'
A
B
C
α
A'
B'
C'
α
成立
2
正切
A
B
C
α
A'
B'
C'
α
由于∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'.
A'C'
AC
B'C'
BC
=
即
AC
BC
A'C'
B'C'
=
2
正切
归纳:在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与邻边的比也是一个固定值.
B
A
C
c
a
b
对边
邻边
定义:在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与邻边的比叫做∠A的正切,记作 tanA .
∠A的对边
∠A的斜边
tan A = =
b
a
2
正切
练一练:在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )
A.3
B.
C.
D.
A
3
锐角三角函数
B
A
C
c
a
b
斜边
邻边
对边
∠A的对边
斜边
sin A = =
c
a
∠A的邻边
斜边
cos A = =
c
b
∠A的对边
∠A的斜边
tan A = =
b
a
定义:在 Rt△ABC 中,∠C=90°,我们把∠A的正弦、余弦和正切,叫作 ∠A的锐角三角函数 .
3
锐角三角函数
例 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
sinA= = ,
AB
BC
5
3
cosA= = ,
AB
AC
5
4
tanA= = .
AB
BC
4
3
因此
3
锐角三角函数
练一练:已知在Rt△ABC中,∠C=90°,AB=7,BC=5,那么下列式子中正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.tanA=
A
随堂练习
1.△ABC在正方形网格中的位置如图所示,则cosα的值是( )
A.
B.
C.
D.
C
2.如图,在Rt△ABC中,∠C=90°.
(1)若AC=6,BC=8,则cosA=________;
(2)若AC=5,cosA= ,则AB=_________.
5
3
13
3.如图,P(12,a)在反比例函数y= 的图象上,PH⊥x轴于点H,则tan∠POH的值为__________.
x
60
12
5
4. 如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
解:∵MN⊥AB,
∴∠ANM=90°,
∴∠A+∠AMN=90°.
∵∠C=90°,
∴∠A+∠B=90°,
∴∠B=∠AMN,
∴cosB=cos∠AMN.
在Rt△AMN中,
∴cos∠AMN= = ,
AM
MN
∴cosB= .
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若BC=2,AB=3,求tan∠BCD的值.
解:∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°.
∵∠BCD+∠ACD=∠ACB=90°,
∴∠BCD=∠A.
在Rt△ABC中,
∴tanA= = ,
AC
BC
∴tan∠BCD=tanA= .
6.在Rt△ABC中,∠C=90°,AB=25,BC=7.
(1)求AC的长;
(2)求锐角A的正弦值、余弦值和正切值.
解:(1)由勾股定理得
(2)sinA= = ,
AB
BC
25
7
cosA= = ,
AB
AC
25
24
tanA= = .
AB
BC
24
7
课堂小结
余弦与正切
余弦
B
A
C
c
a
b
斜边
邻边
正切
B
A
C
c
a
b
对边
邻边
锐角三角函数
∠A的邻边
斜边
cos A = =
c
b
∠A的对边
∠A的斜边
tan A = =
b
a
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
28.1 锐角三角函数
第二十八章 锐角三角函数
课程讲授
新知导入
随堂练习
课堂小结
第2课时 余弦与正切
知识要点
1.余弦
2.正切
3.锐角三角函数
新知导入
试一试:根据所学知识,按要求完成下列问题。
A
B
C
B'
B''
C'
C''
根据正弦的定义sinA= = =
AB
BC
A'B'
B'C'
A''B''
B''C''
课程讲授
1
余弦
问题1:如图, △ABC 和 △A'B'C'都是直角三角形, 其中∠A =∠A',∠C =∠C' = 90°,则 = 成立吗?为什么?
AB
AC
A'B'
A'C'
A
B
C
α
A'
B'
C'
α
成立
1
余弦
A
B
C
α
A'
B'
C'
α
由于∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'.
∠B=∠B',
sinB = sinB',
AB
AC
A'B'
A'C'
=
即
1
余弦
归纳:在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的邻边与斜边的比也是一个固定值.
B
A
C
c
a
b
斜边
邻边
定义:在 Rt△ABC 中,∠C=90°,我们把锐角 A 的邻边与斜边的比叫做∠A的余弦,记作 cosA .
∠A的邻边
斜边
cos A = =
c
b
1
余弦
A
B
C
α
sinB = cosA,
看出,对于任意锐角α,有
cos α = sin (90°-α)
1
余弦
练一练:如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是( )
A.
B.
C.
D.
A
2
正切
问题1:如图, △ABC 和 △A'B'C'都是直角三角形, 其中∠A =∠A',∠C =∠C' = 90°,则 = 成立吗?为什么?
AC
BC
A'C'
B'C'
A
B
C
α
A'
B'
C'
α
成立
2
正切
A
B
C
α
A'
B'
C'
α
由于∠C=∠C'=90°,∠A=∠A'=α,
所以Rt△ABC ∽Rt△A'B'C'.
A'C'
AC
B'C'
BC
=
即
AC
BC
A'C'
B'C'
=
2
正切
归纳:在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A 的对边与邻边的比也是一个固定值.
B
A
C
c
a
b
对边
邻边
定义:在 Rt△ABC 中,∠C=90°,我们把锐角 A 的对边与邻边的比叫做∠A的正切,记作 tanA .
∠A的对边
∠A的斜边
tan A = =
b
a
2
正切
练一练:在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )
A.3
B.
C.
D.
A
3
锐角三角函数
B
A
C
c
a
b
斜边
邻边
对边
∠A的对边
斜边
sin A = =
c
a
∠A的邻边
斜边
cos A = =
c
b
∠A的对边
∠A的斜边
tan A = =
b
a
定义:在 Rt△ABC 中,∠C=90°,我们把∠A的正弦、余弦和正切,叫作 ∠A的锐角三角函数 .
3
锐角三角函数
例 如图,在 Rt△ABC 中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
A
B
C
10
6
解:由勾股定理得
sinA= = ,
AB
BC
5
3
cosA= = ,
AB
AC
5
4
tanA= = .
AB
BC
4
3
因此
3
锐角三角函数
练一练:已知在Rt△ABC中,∠C=90°,AB=7,BC=5,那么下列式子中正确的是( )
A.sinA=
B.cosA=
C.tanA=
D.tanA=
A
随堂练习
1.△ABC在正方形网格中的位置如图所示,则cosα的值是( )
A.
B.
C.
D.
C
2.如图,在Rt△ABC中,∠C=90°.
(1)若AC=6,BC=8,则cosA=________;
(2)若AC=5,cosA= ,则AB=_________.
5
3
13
3.如图,P(12,a)在反比例函数y= 的图象上,PH⊥x轴于点H,则tan∠POH的值为__________.
x
60
12
5
4. 如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
解:∵MN⊥AB,
∴∠ANM=90°,
∴∠A+∠AMN=90°.
∵∠C=90°,
∴∠A+∠B=90°,
∴∠B=∠AMN,
∴cosB=cos∠AMN.
在Rt△AMN中,
∴cos∠AMN= = ,
AM
MN
∴cosB= .
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若BC=2,AB=3,求tan∠BCD的值.
解:∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°.
∵∠BCD+∠ACD=∠ACB=90°,
∴∠BCD=∠A.
在Rt△ABC中,
∴tanA= = ,
AC
BC
∴tan∠BCD=tanA= .
6.在Rt△ABC中,∠C=90°,AB=25,BC=7.
(1)求AC的长;
(2)求锐角A的正弦值、余弦值和正切值.
解:(1)由勾股定理得
(2)sinA= = ,
AB
BC
25
7
cosA= = ,
AB
AC
25
24
tanA= = .
AB
BC
24
7
课堂小结
余弦与正切
余弦
B
A
C
c
a
b
斜边
邻边
正切
B
A
C
c
a
b
对边
邻边
锐角三角函数
∠A的邻边
斜边
cos A = =
c
b
∠A的对边
∠A的斜边
tan A = =
b
a
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
