28.1锐角三角函数(特殊锐角的三角函数值)第3课时 课件
文档属性
| 名称 | 28.1锐角三角函数(特殊锐角的三角函数值)第3课时 课件 |  | |
| 格式 | rar | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 15:57:01 | ||
图片预览





文档简介
(共18张PPT)
28.1 锐角三角函数
第二十八章 锐角三角函数
课程讲授
新知导入
随堂练习
课堂小结
第3课时 特殊锐角的三角函数值
知识要点
1.特殊角的三角函数值
2.由三角函数值求特殊角
新知导入
看一看:观察手中的三角板,试着归纳它们边和角之间的规律。
A
B
C
45°
A
B
C
30°
sin A=sinB= cos A
AC=BC
tan A=1
2BC=AB
sin A= cosB=
2
1
课程讲授
1
特殊角的三角函数值
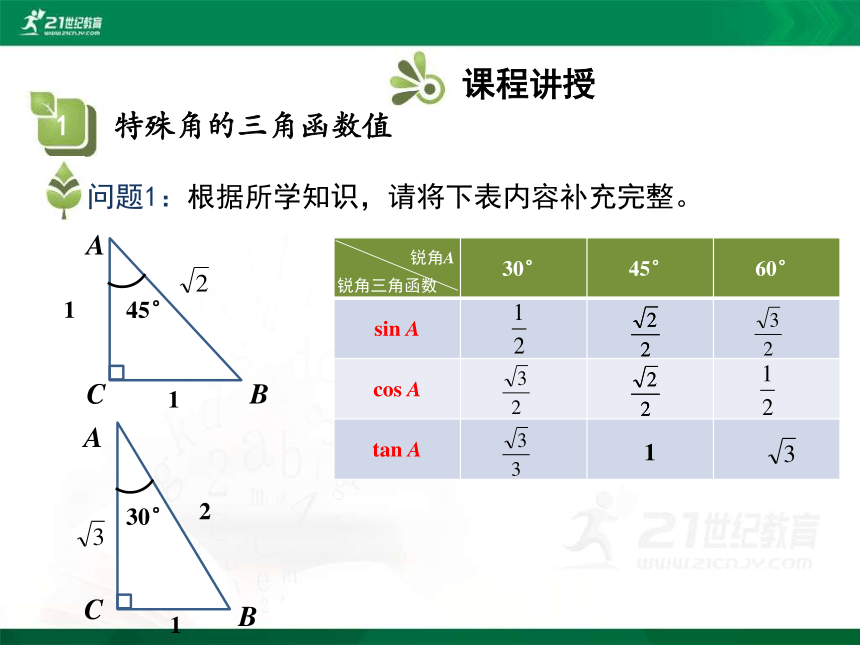
问题1:根据所学知识,请将下表内容补充完整。
A
B
C
45°
A
B
C
30°
30° 45° 60°
sin A
cos A
tan A
锐角A
锐角三角函数
1
2
1
1
1
1
特殊角的三角函数值
例 求下列各式的值:
(1) cos260°+sin260°;
解:cos260°+sin260°
=1
1
特殊角的三角函数值
例 求下列各式的值:
(2) -tan45°;
sin45°
cos45°
解: -tan45°;
sin45°
cos45°
=0
1
特殊角的三角函数值
练一练:cos30°的值等于( )
A.
B.
C.1
D.
B
2
由三角函数值求特殊角
例 (1) 如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
A
B
C
解: 在图中,
∵sin A= = = ,
AB
BC
∴∠A=90°.
2
由三角函数值求特殊角
例 (2) 如图,AO 是圆锥的高,OB 是底面半径,AO =
OB,求 α 的度数.
A
B
O
解: 在图中,
∵tan A= = = ,
OB
AO
∴α=60°.
2
由三角函数值求特殊角
练一练:在△ABC中,∠C=90°,sinA= ,那么∠A的度数为( )
A.60°
B.45°
C.30°
D.30°或60°
C
随堂练习
1.2sin60°等于( )
A.1 B.
C. D.
2.cos60°+ tan45°的值等于( )
A.
B.
C.
D.1
B
A
3.在△ABC中,∠A,∠B都是锐角,tanA=1,sinB= ,则△ABC最确切的形状是( )
A.等腰三角形
B.等腰直角三角形
C.直角三角形
D.锐角三角形
B
4.把一个直尺与一块三角板按如图所示放置,若sin∠1= ,则∠2的度数为( )
A.120°
B.135°
C.145°
D.150°
B
5.计算:
(1)sin30°÷cos45°=_________;
(2)cos30°·tan30°-tan45°=_________;
(3)sin260°+cos260°=_________;
6.在Rt△ABC中,∠C=90°,BC=8且tanA= ,则AB=________.
1
16
7.一个小孩荡秋千,秋千链子的长度为4 m,秋千向两边摆动的幅度相同,简化图如图所示,OA,OB,OC均为秋千长,∠AOB为摆动角.当秋千升高2 m时,求秋千的摆动角的度数.
∴秋千的摆动角∠AOB=∠AOD+∠BOD=120°.
解:由题意,得OA=OC=4 m,CD=2 m,
∴OD=2 m.
∵∠ADO=90°,
∴cos∠AOD= = ,
OA
2
OD
1
∴∠AOD=60°.
由题意可知∠BOD=∠AOD=60°,
课堂小结
特殊锐角的三角函数值
30°、45°和60°的三角函数值
sin30°= ,cos30°= ,tan30°=
sin45°= ,cos45°= ,tan45°= 1
sin60°= ,cos60°= ,tan60°= ,
由三角函数值求特殊角
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
28.1 锐角三角函数
第二十八章 锐角三角函数
课程讲授
新知导入
随堂练习
课堂小结
第3课时 特殊锐角的三角函数值
知识要点
1.特殊角的三角函数值
2.由三角函数值求特殊角
新知导入
看一看:观察手中的三角板,试着归纳它们边和角之间的规律。
A
B
C
45°
A
B
C
30°
sin A=sinB= cos A
AC=BC
tan A=1
2BC=AB
sin A= cosB=
2
1
课程讲授
1
特殊角的三角函数值
问题1:根据所学知识,请将下表内容补充完整。
A
B
C
45°
A
B
C
30°
30° 45° 60°
sin A
cos A
tan A
锐角A
锐角三角函数
1
2
1
1
1
1
特殊角的三角函数值
例 求下列各式的值:
(1) cos260°+sin260°;
解:cos260°+sin260°
=1
1
特殊角的三角函数值
例 求下列各式的值:
(2) -tan45°;
sin45°
cos45°
解: -tan45°;
sin45°
cos45°
=0
1
特殊角的三角函数值
练一练:cos30°的值等于( )
A.
B.
C.1
D.
B
2
由三角函数值求特殊角
例 (1) 如图,在Rt△ABC中,∠C = 90°,AB = ,
BC = ,求 ∠A 的度数;
A
B
C
解: 在图中,
∵sin A= = = ,
AB
BC
∴∠A=90°.
2
由三角函数值求特殊角
例 (2) 如图,AO 是圆锥的高,OB 是底面半径,AO =
OB,求 α 的度数.
A
B
O
解: 在图中,
∵tan A= = = ,
OB
AO
∴α=60°.
2
由三角函数值求特殊角
练一练:在△ABC中,∠C=90°,sinA= ,那么∠A的度数为( )
A.60°
B.45°
C.30°
D.30°或60°
C
随堂练习
1.2sin60°等于( )
A.1 B.
C. D.
2.cos60°+ tan45°的值等于( )
A.
B.
C.
D.1
B
A
3.在△ABC中,∠A,∠B都是锐角,tanA=1,sinB= ,则△ABC最确切的形状是( )
A.等腰三角形
B.等腰直角三角形
C.直角三角形
D.锐角三角形
B
4.把一个直尺与一块三角板按如图所示放置,若sin∠1= ,则∠2的度数为( )
A.120°
B.135°
C.145°
D.150°
B
5.计算:
(1)sin30°÷cos45°=_________;
(2)cos30°·tan30°-tan45°=_________;
(3)sin260°+cos260°=_________;
6.在Rt△ABC中,∠C=90°,BC=8且tanA= ,则AB=________.
1
16
7.一个小孩荡秋千,秋千链子的长度为4 m,秋千向两边摆动的幅度相同,简化图如图所示,OA,OB,OC均为秋千长,∠AOB为摆动角.当秋千升高2 m时,求秋千的摆动角的度数.
∴秋千的摆动角∠AOB=∠AOD+∠BOD=120°.
解:由题意,得OA=OC=4 m,CD=2 m,
∴OD=2 m.
∵∠ADO=90°,
∴cos∠AOD= = ,
OA
2
OD
1
∴∠AOD=60°.
由题意可知∠BOD=∠AOD=60°,
课堂小结
特殊锐角的三角函数值
30°、45°和60°的三角函数值
sin30°= ,cos30°= ,tan30°=
sin45°= ,cos45°= ,tan45°= 1
sin60°= ,cos60°= ,tan60°= ,
由三角函数值求特殊角
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
