28.1锐角三角函数(用计算器计算锐角三角函数值)第4课时 课件
文档属性
| 名称 | 28.1锐角三角函数(用计算器计算锐角三角函数值)第4课时 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 16:18:06 | ||
图片预览








文档简介
(共23张PPT)
28.1 锐角三角函数
第二十八章 锐角三角函数
课程讲授
新知导入
随堂练习
课堂小结
第4课时 用计算器计算锐角三角函数值
知识要点
1.用计算器求一个锐角三角函数的值
2.已知锐角的三角函数值求锐角
3.探究锐角三角函数的性质
新知导入
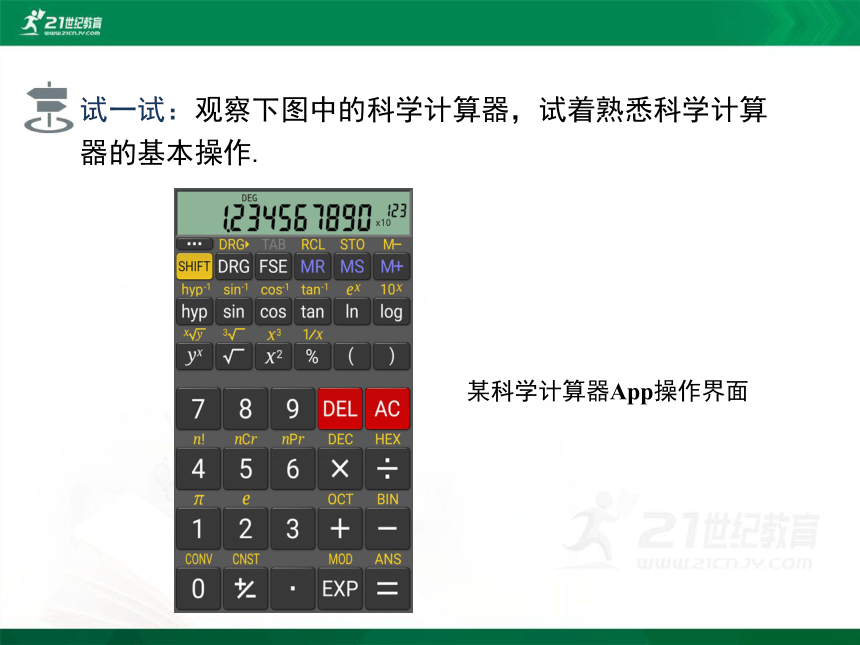
试一试:观察下图中的科学计算器,试着熟悉科学计算器的基本操作.
试一试:观察下图中的科学计算器,试着熟悉科学计算器的基本操作.
某科学计算器App操作界面
课程讲授
1
用计算器求一个锐角三角函数的值
例1 用计算器求sin18°的值;
解:第一步:按计算器 键;
sin
第二步:输入角度值18;
屏幕显示结果
sin18°= 0.309 016 994
1
用计算器求一个锐角三角函数的值
例1 用计算器求 tan30°36′ 的值;
解:方法1:
第一步:按计算器 键;
tan
第二步:输入角度值30.6 (因为30°36′ = 30.6°);
屏幕显示结果
0.591 398 351
1
用计算器求一个锐角三角函数的值
例1 用计算器求 tan30°36′ 的值;
解:方法2:
第一步:按计算器 键;
tan
屏幕显示结果
0.591 398 351
第二步:输入角度值30,分值36 (使用 键);
° ′ ″
1
用计算器求一个锐角三角函数的值
练一练:用计算器求sin24°37′18″的值,以下按键顺序正确的是( )
A.
B.
C.
D.
A
2
已知锐角的三角函数值求锐角
例 已知 sinA = 0.5018,用计算器求 ∠A 的度数.
解:第一步:按计算器 键;
2nd F
sin
第二步:然后输入函数值0. 5018;
屏幕显示结果
30.119 158 67°
还可以利用 键,进一步得到∠A = 30°07′08.97 ″ (这说明锐角 A 精确到 1′ 的结果为 30°7′,精确到 1″ 的结果为30°7′9″).
2nd F
° ′ ″
2
已知锐角的三角函数值求锐角
练一练:已知sinα=0.3090,则α约为( )
A.17°
B.18°
C.19°
D.20°
B
3
探究锐角三角函数的性质
问题1:通过科学计算器计算 ,比较下列各对数的大小,并提出你的猜想:
(1) sin23°____cos67°;
sin33°____cos57°;
sin46°____cos44°;
=
=
=
sinA____cos(90°-A);0<∠A<<90°
=
3
探究锐角三角函数的性质
(2) tan23°____tan67°;
tan33°____tan57°;
tan46°____tan44°;
<
<
<
tanA____tan(90°-A)(A<45°);
<
问题1:通过科学计算器计算 ,比较下列各对数的大小,并提出你的猜想:
0<∠A<∠B<90°,tanA____tanB;
<
3
探究锐角三角函数的性质
练一练:∠A为锐角,且 <cosA< ,∠A的取值范围是( )
A.0<∠A<30°
B.30°<∠A<60°
C.60°<∠A<90°
D.30°<∠A<45°
B
随堂练习
1.下列说法正确的是( )
A.求sin30°的按键顺序是
B.求23的按键顺序
C.求 的按键顺序是
D.已知sinA=0.5018,用计算器求锐角∠A的大小,按键顺序是
A
2.利用计算器求值:(保留4位小数)
(1)sin67°38′24″≈___________;
(2)sin23°5′+cos66°55′≈___________;
(3)289.4×sin47°34′25″≈___________;
(4)sin18°+cos55°-tan59°≈___________.
0.9248
0.7841
213.6191
-0.7817
3.求下列各角的度数:(精确到1″)
(1)若cosA=0.6753(∠A为锐角),则∠A≈___________;
(2)若sinB=0.4553(∠B为锐角),则∠B≈___________;
(3)若tanC=0.1890(∠C为锐角),则∠C≈___________.
47°31′21″
27°5′3″
10°42′10″
4.∠α和∠β如图所示,tanα与tanβ的大小关系是________________.
tanα<tanβ
5.如图,在Rt△ABC中,∠C=90°,AC=3,∠B=37°,则BC的长约为___________.(结果保留整数)
4
6.如图,在△ABC中,AB=8,AC=9,∠A=48°.求:
(1)AB边上的高;(精确到0.01)
(2)∠B的度数.(精确到1′)
解:(1)作AB边上的高CH,垂足为点H.
∵在Rt△ACH中,
∴CH=AC·sinA=9sin48°≈6.69.
H
sinA= ,
AC
CH
6.如图,在△ABC中,AB=8,AC=9,∠A=48°.求:
(1)AB边上的高;(精确到0.01)
(2)∠B的度数.(精确到1′)
∴∠B≈73°32′.
解:(2)∵在Rt△ACH中,
∴AH=AC·cosA=9cos48°.
在Rt△BCH中,
≈3.382,
cosA= ,
AC
AH
tanB= =
BH
CH
AB-AH
CH
=
8-9cos48°
9sin48°
H
课堂小结
用计算器计算锐角三角函数值
用计算器求一个锐角三角函数的值
已知锐角的三角函数值求锐角
探究锐角三角函数的性质
sinA=cos(90°-A);0<∠A<90°
0<∠A<∠B<90°,tanA谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
28.1 锐角三角函数
第二十八章 锐角三角函数
课程讲授
新知导入
随堂练习
课堂小结
第4课时 用计算器计算锐角三角函数值
知识要点
1.用计算器求一个锐角三角函数的值
2.已知锐角的三角函数值求锐角
3.探究锐角三角函数的性质
新知导入
试一试:观察下图中的科学计算器,试着熟悉科学计算器的基本操作.
试一试:观察下图中的科学计算器,试着熟悉科学计算器的基本操作.
某科学计算器App操作界面
课程讲授
1
用计算器求一个锐角三角函数的值
例1 用计算器求sin18°的值;
解:第一步:按计算器 键;
sin
第二步:输入角度值18;
屏幕显示结果
sin18°= 0.309 016 994
1
用计算器求一个锐角三角函数的值
例1 用计算器求 tan30°36′ 的值;
解:方法1:
第一步:按计算器 键;
tan
第二步:输入角度值30.6 (因为30°36′ = 30.6°);
屏幕显示结果
0.591 398 351
1
用计算器求一个锐角三角函数的值
例1 用计算器求 tan30°36′ 的值;
解:方法2:
第一步:按计算器 键;
tan
屏幕显示结果
0.591 398 351
第二步:输入角度值30,分值36 (使用 键);
° ′ ″
1
用计算器求一个锐角三角函数的值
练一练:用计算器求sin24°37′18″的值,以下按键顺序正确的是( )
A.
B.
C.
D.
A
2
已知锐角的三角函数值求锐角
例 已知 sinA = 0.5018,用计算器求 ∠A 的度数.
解:第一步:按计算器 键;
2nd F
sin
第二步:然后输入函数值0. 5018;
屏幕显示结果
30.119 158 67°
还可以利用 键,进一步得到∠A = 30°07′08.97 ″ (这说明锐角 A 精确到 1′ 的结果为 30°7′,精确到 1″ 的结果为30°7′9″).
2nd F
° ′ ″
2
已知锐角的三角函数值求锐角
练一练:已知sinα=0.3090,则α约为( )
A.17°
B.18°
C.19°
D.20°
B
3
探究锐角三角函数的性质
问题1:通过科学计算器计算 ,比较下列各对数的大小,并提出你的猜想:
(1) sin23°____cos67°;
sin33°____cos57°;
sin46°____cos44°;
=
=
=
sinA____cos(90°-A);0<∠A<<90°
=
3
探究锐角三角函数的性质
(2) tan23°____tan67°;
tan33°____tan57°;
tan46°____tan44°;
<
<
<
tanA____tan(90°-A)(A<45°);
<
问题1:通过科学计算器计算 ,比较下列各对数的大小,并提出你的猜想:
0<∠A<∠B<90°,tanA____tanB;
<
3
探究锐角三角函数的性质
练一练:∠A为锐角,且 <cosA< ,∠A的取值范围是( )
A.0<∠A<30°
B.30°<∠A<60°
C.60°<∠A<90°
D.30°<∠A<45°
B
随堂练习
1.下列说法正确的是( )
A.求sin30°的按键顺序是
B.求23的按键顺序
C.求 的按键顺序是
D.已知sinA=0.5018,用计算器求锐角∠A的大小,按键顺序是
A
2.利用计算器求值:(保留4位小数)
(1)sin67°38′24″≈___________;
(2)sin23°5′+cos66°55′≈___________;
(3)289.4×sin47°34′25″≈___________;
(4)sin18°+cos55°-tan59°≈___________.
0.9248
0.7841
213.6191
-0.7817
3.求下列各角的度数:(精确到1″)
(1)若cosA=0.6753(∠A为锐角),则∠A≈___________;
(2)若sinB=0.4553(∠B为锐角),则∠B≈___________;
(3)若tanC=0.1890(∠C为锐角),则∠C≈___________.
47°31′21″
27°5′3″
10°42′10″
4.∠α和∠β如图所示,tanα与tanβ的大小关系是________________.
tanα<tanβ
5.如图,在Rt△ABC中,∠C=90°,AC=3,∠B=37°,则BC的长约为___________.(结果保留整数)
4
6.如图,在△ABC中,AB=8,AC=9,∠A=48°.求:
(1)AB边上的高;(精确到0.01)
(2)∠B的度数.(精确到1′)
解:(1)作AB边上的高CH,垂足为点H.
∵在Rt△ACH中,
∴CH=AC·sinA=9sin48°≈6.69.
H
sinA= ,
AC
CH
6.如图,在△ABC中,AB=8,AC=9,∠A=48°.求:
(1)AB边上的高;(精确到0.01)
(2)∠B的度数.(精确到1′)
∴∠B≈73°32′.
解:(2)∵在Rt△ACH中,
∴AH=AC·cosA=9cos48°.
在Rt△BCH中,
≈3.382,
cosA= ,
AC
AH
tanB= =
BH
CH
AB-AH
CH
=
8-9cos48°
9sin48°
H
课堂小结
用计算器计算锐角三角函数值
用计算器求一个锐角三角函数的值
已知锐角的三角函数值求锐角
探究锐角三角函数的性质
sinA=cos(90°-A);0<∠A<90°
0<∠A<∠B<90°,tanA
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
