第二十八章 锐角三角函数 章末复习与小结 课件
文档属性
| 名称 | 第二十八章 锐角三角函数 章末复习与小结 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
章末复习与小结
第二十八章 锐角三角函数
专题选讲
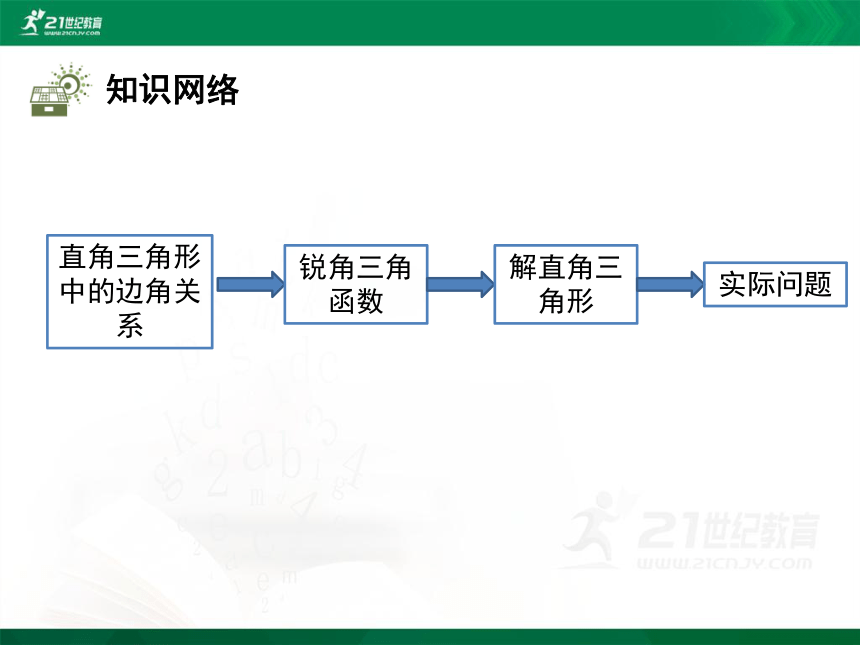
知识网络
重难突破
课后习题
知识网络
直角三角形中的边角关系
锐角三角函数
解直角三角形
实际问题
方法专题15 求锐角三角函数值常用的方法
本章专题索引
专题选讲
方法专题16 巧用锐角三角函数解决实际问题
专题选讲—— 求锐角三角函数值常用的方法
类型一 回归定义
例 如图,在Rt△ABC中,∠C=90°,BC=6,tanA= ,求AB的长和sinB的值.
解:∵在Rt△ABC中,
∴AC=12,
∠C=90°,BC=6,tanA= = ,
∴ ,
∴sinB= = = .
类型一 回归定义
在求某一个锐角三角函数值时,应首先考虑锐角三角函数的定义,观察该锐角三角函数应是哪两条边的比,再求对应边的长度.
方法归纳
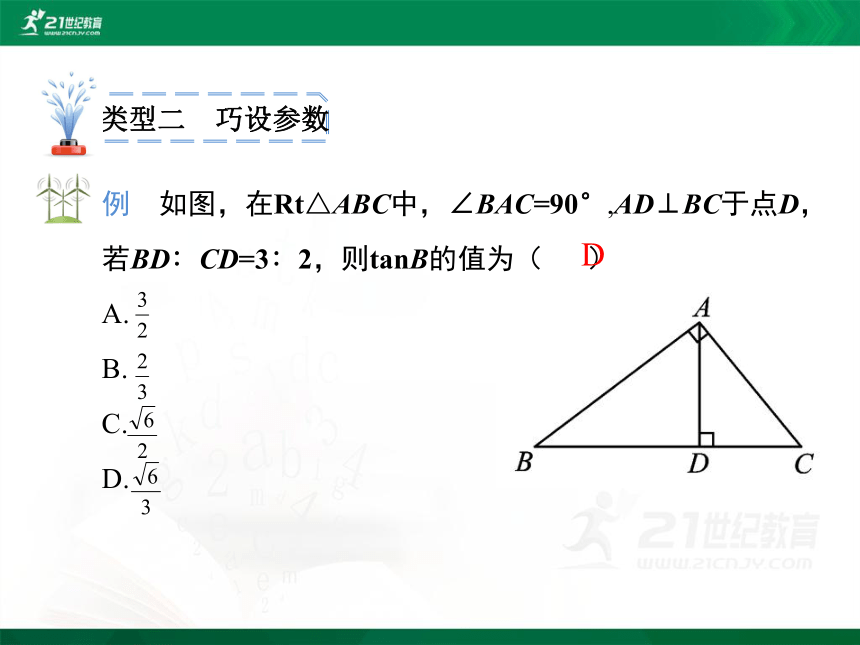
类型二 巧设参数
例 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tanB的值为( )
A.
B.
C.
D.
D
类型二 巧设参数
当已知条件是线段之比或某锐角三角函数值时,考虑设一参数,把直角三角形的三边都用该参数的代数式表示出来,然后求解.
方法归纳
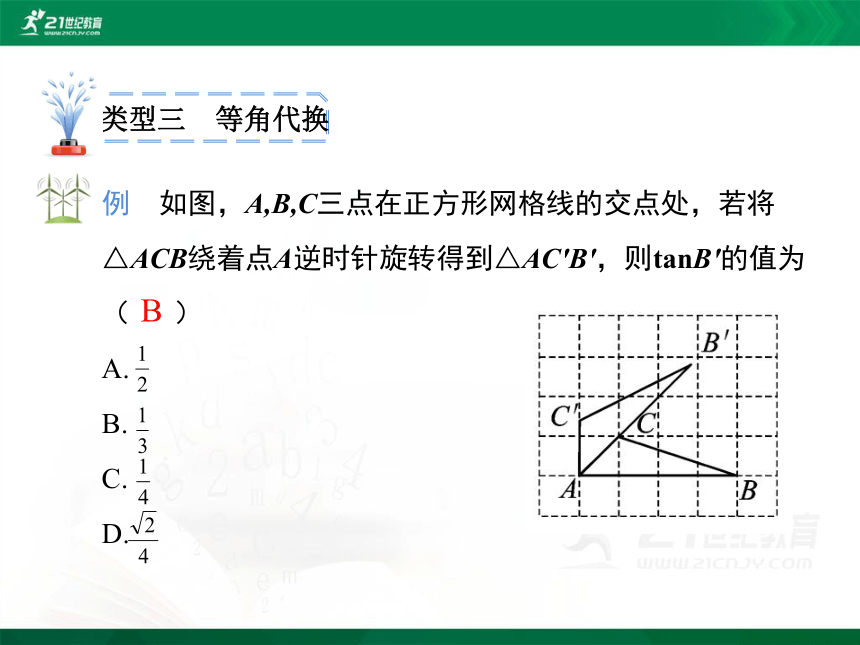
类型三 等角代换
例 如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A.
B.
C.
D.
B
类型三 等角代换
如果两个锐角相等,那么这两个锐角的三角函数值也相等.当求某个锐角的三角函数值发生困难时,可考虑能否用一个与之相等且易求三角函数值的角来代换.
方法归纳
类型四 构造直角三角形
例 在△ABC中,AB=AC=13,BC=24,则tanB等于( )
A.
B.
C.
D.
B
类型四 构造直角三角形
当所求的锐角不在直角三角形中时,考虑添加辅助线建立直角三角形,把该锐角摆放在直角三角形中,再根据已知条件求解.
方法归纳
专题选讲—— 巧用锐角三角函数解决实际问题
类型一 构造单一直角三角形解决实际问题
例 如图,小明沿着坡比为1∶3的山坡向上走了600 m(即AB的长),则他升高了( )
A. m
B. m
C.300 m
D.200 m
C
类型二 构造共直角边的两直角三角形解决实际问题
例 如图,港口A在观测站O的正东方向,OA=6 km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A. km
B. km
C.4 km
D. km
A
类型三 构造不共直角边的两直角三角形解决实际问题
例 如图,校园内有两幢高度相同的教学楼AB,CD,大楼的底部B,D在同一平面上,两幢楼之间的距离BD长为24米,小明在点E(B,E,D在一条直线上)处测得教学楼AB顶部的仰角为45°,然后沿EB方向前进8米到达点G处,测得教学楼CD顶部的仰角为30°.已知小明的两个观测点F,H距离地面的高度均为1.6米,求教学楼AB的高度.(结果精确到0.1米)
类型三 构造不共直角边的两直角三角形解决实际问题
解:延长HF交CD于点N,延长FH交AB于点M,
由题意可得MB=HG=FE=ND=1.6米,
HF=GE=8米,
MF=BE,HN=GD,MN=BD=24米.
∵AB=CD,
∴AB-BM=CD-ND,
即AM=CN.
M
N
类型三 构造不共直角边的两直角三角形解决实际问题
答:教学楼AB的高度约为13.3米.
设AM=CN=x米.
在Rt△AFM中,∠AFM=45°,
∴MF=AM=x米.
在Rt△CNH中,∠CHN=30°,
∵HF=MF+HN-MN=8米,
解得x≈11.7,
∴AM≈11.7米.
∴AB=AM+BM=11.7+1.6=13.3(米).
∴x+ x-24=8,
∴ (米).
M
N
类型三 构造不共直角边的两直角三角形解决实际问题
解直角三角形实际应用题的常见图形类型及辅助线作法如下:
方法归纳
类型四 构造特殊的四边形和直角三角形解决实际问题
例 如图,某水库拦水大坝的横断面为梯形ABCD,其中迎水坡AB的坡角α=45°,坡长AB= 米,背水坡CD的坡度i=1∶ ,则背水坡的坡长CD为________米.
20
类型四 构造特殊的四边形和直角三角形解决实际问题
对于解直角三角形的实际应用题,要灵活运用转化思想,通常是根据以下方法和步骤解决:(1)有图的要首先将题干中的已知量在图中表示出来,找到与已知量和未知量相关联的三角形,弄清楚已知条件中各量之间的关系.
方法归纳
类型四 构造特殊的四边形和直角三角形解决实际问题
(2)若三角形是直角三角形,根据边角关系进行计算;若三角形不是直角三角形,可通过添加辅助线构造直角三角形来解决,其中作某边上的高是常用的辅助线.(3)在构造直角三角形时,要注意把所有的特殊角或已知的三角函数值的角、已知条件都能摆在已建立的直角三角形中.
方法归纳
重难突破
锐角三角函数
1
C
例1 △ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于点D,下列四个选项中,错误的是( )
A.sinα=cosα
B.tanC=2
C.sinβ=cosβ
D.tanα=1
解直角三角形
2
例2 (8分)如图,AD是△ABC的中线,tanB= ,cosC= ,AC= .求:
(1)BC的长;
(2)sin∠ADC的值.
解直角三角形
2
(1分)
(2分)
(3分)
(4分)
解:(1)过点A作AE⊥BC于点E.
在Rt△ACE中,cosC= ,AC= ,
∴CE=AC·cosC=1,
∴AE= =1.
在Rt△ABE中,
tanB= = ,
AE
BE
∴BE=3AE=3.
∴BC=BE+CE=3+1=4.
解直角三角形
2
(6分)
(8分)
(2)∵AD是△ABC的中线,
∴CD= BC=2,
∴DE=CD-CE=2-1=1.
∵AE=1,
∴DE=AE.
又∵AE⊥BC,
∴∠ADC=45°,
∴sin∠ADC= .
解直角三角形的应用
3
例3 (6分)为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离.(结果保留根号)
解直角三角形的应用
3
(1分)
(3分)
(5分)
(6分)
解:过点P作PC⊥AB于点C.
由题意可知∠PAC=60°,∠PBC=30°.
在Rt△PAC中,
∵ =tan∠PAC,
在Rt△PBC中,
∴AC= PC.
∵ =tan∠PBC,
∴BC= PC.
∵AB=AC+BC=10×40=400(米),
∴ PC+ PC=400,
∴PC=100 米.
答:建筑物P到赛道AB的距离为100 米.
课后习题
第二十八章 锐角三角函数 复习题28P84—P85
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
章末复习与小结
第二十八章 锐角三角函数
专题选讲
知识网络
重难突破
课后习题
知识网络
直角三角形中的边角关系
锐角三角函数
解直角三角形
实际问题
方法专题15 求锐角三角函数值常用的方法
本章专题索引
专题选讲
方法专题16 巧用锐角三角函数解决实际问题
专题选讲—— 求锐角三角函数值常用的方法
类型一 回归定义
例 如图,在Rt△ABC中,∠C=90°,BC=6,tanA= ,求AB的长和sinB的值.
解:∵在Rt△ABC中,
∴AC=12,
∠C=90°,BC=6,tanA= = ,
∴ ,
∴sinB= = = .
类型一 回归定义
在求某一个锐角三角函数值时,应首先考虑锐角三角函数的定义,观察该锐角三角函数应是哪两条边的比,再求对应边的长度.
方法归纳
类型二 巧设参数
例 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tanB的值为( )
A.
B.
C.
D.
D
类型二 巧设参数
当已知条件是线段之比或某锐角三角函数值时,考虑设一参数,把直角三角形的三边都用该参数的代数式表示出来,然后求解.
方法归纳
类型三 等角代换
例 如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A.
B.
C.
D.
B
类型三 等角代换
如果两个锐角相等,那么这两个锐角的三角函数值也相等.当求某个锐角的三角函数值发生困难时,可考虑能否用一个与之相等且易求三角函数值的角来代换.
方法归纳
类型四 构造直角三角形
例 在△ABC中,AB=AC=13,BC=24,则tanB等于( )
A.
B.
C.
D.
B
类型四 构造直角三角形
当所求的锐角不在直角三角形中时,考虑添加辅助线建立直角三角形,把该锐角摆放在直角三角形中,再根据已知条件求解.
方法归纳
专题选讲—— 巧用锐角三角函数解决实际问题
类型一 构造单一直角三角形解决实际问题
例 如图,小明沿着坡比为1∶3的山坡向上走了600 m(即AB的长),则他升高了( )
A. m
B. m
C.300 m
D.200 m
C
类型二 构造共直角边的两直角三角形解决实际问题
例 如图,港口A在观测站O的正东方向,OA=6 km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A. km
B. km
C.4 km
D. km
A
类型三 构造不共直角边的两直角三角形解决实际问题
例 如图,校园内有两幢高度相同的教学楼AB,CD,大楼的底部B,D在同一平面上,两幢楼之间的距离BD长为24米,小明在点E(B,E,D在一条直线上)处测得教学楼AB顶部的仰角为45°,然后沿EB方向前进8米到达点G处,测得教学楼CD顶部的仰角为30°.已知小明的两个观测点F,H距离地面的高度均为1.6米,求教学楼AB的高度.(结果精确到0.1米)
类型三 构造不共直角边的两直角三角形解决实际问题
解:延长HF交CD于点N,延长FH交AB于点M,
由题意可得MB=HG=FE=ND=1.6米,
HF=GE=8米,
MF=BE,HN=GD,MN=BD=24米.
∵AB=CD,
∴AB-BM=CD-ND,
即AM=CN.
M
N
类型三 构造不共直角边的两直角三角形解决实际问题
答:教学楼AB的高度约为13.3米.
设AM=CN=x米.
在Rt△AFM中,∠AFM=45°,
∴MF=AM=x米.
在Rt△CNH中,∠CHN=30°,
∵HF=MF+HN-MN=8米,
解得x≈11.7,
∴AM≈11.7米.
∴AB=AM+BM=11.7+1.6=13.3(米).
∴x+ x-24=8,
∴ (米).
M
N
类型三 构造不共直角边的两直角三角形解决实际问题
解直角三角形实际应用题的常见图形类型及辅助线作法如下:
方法归纳
类型四 构造特殊的四边形和直角三角形解决实际问题
例 如图,某水库拦水大坝的横断面为梯形ABCD,其中迎水坡AB的坡角α=45°,坡长AB= 米,背水坡CD的坡度i=1∶ ,则背水坡的坡长CD为________米.
20
类型四 构造特殊的四边形和直角三角形解决实际问题
对于解直角三角形的实际应用题,要灵活运用转化思想,通常是根据以下方法和步骤解决:(1)有图的要首先将题干中的已知量在图中表示出来,找到与已知量和未知量相关联的三角形,弄清楚已知条件中各量之间的关系.
方法归纳
类型四 构造特殊的四边形和直角三角形解决实际问题
(2)若三角形是直角三角形,根据边角关系进行计算;若三角形不是直角三角形,可通过添加辅助线构造直角三角形来解决,其中作某边上的高是常用的辅助线.(3)在构造直角三角形时,要注意把所有的特殊角或已知的三角函数值的角、已知条件都能摆在已建立的直角三角形中.
方法归纳
重难突破
锐角三角函数
1
C
例1 △ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于点D,下列四个选项中,错误的是( )
A.sinα=cosα
B.tanC=2
C.sinβ=cosβ
D.tanα=1
解直角三角形
2
例2 (8分)如图,AD是△ABC的中线,tanB= ,cosC= ,AC= .求:
(1)BC的长;
(2)sin∠ADC的值.
解直角三角形
2
(1分)
(2分)
(3分)
(4分)
解:(1)过点A作AE⊥BC于点E.
在Rt△ACE中,cosC= ,AC= ,
∴CE=AC·cosC=1,
∴AE= =1.
在Rt△ABE中,
tanB= = ,
AE
BE
∴BE=3AE=3.
∴BC=BE+CE=3+1=4.
解直角三角形
2
(6分)
(8分)
(2)∵AD是△ABC的中线,
∴CD= BC=2,
∴DE=CD-CE=2-1=1.
∵AE=1,
∴DE=AE.
又∵AE⊥BC,
∴∠ADC=45°,
∴sin∠ADC= .
解直角三角形的应用
3
例3 (6分)为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离.(结果保留根号)
解直角三角形的应用
3
(1分)
(3分)
(5分)
(6分)
解:过点P作PC⊥AB于点C.
由题意可知∠PAC=60°,∠PBC=30°.
在Rt△PAC中,
∵ =tan∠PAC,
在Rt△PBC中,
∴AC= PC.
∵ =tan∠PBC,
∴BC= PC.
∵AB=AC+BC=10×40=400(米),
∴ PC+ PC=400,
∴PC=100 米.
答:建筑物P到赛道AB的距离为100 米.
课后习题
第二十八章 锐角三角函数 复习题28P84—P85
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
