高中数学必修五:3.2《一元二次不等式的解法》教学设计
文档属性
| 名称 | 高中数学必修五:3.2《一元二次不等式的解法》教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-28 15:31:19 | ||
图片预览


文档简介
3.2《一元二次不等式的解法》教学设计
教学目标
(一)知识目标:熟练掌握一元二次不等式解法,理解一元二次方程、一元二次不等式和二次函数之间的关系。
(二)能力目标:培养学生运用等价转化和数形结合等数学思想解决数学问题的能力。
(三)情感目标:通过等与不等的对立统一关系的认识,对学生进行辩证唯物主义教育;经历从实际情景中抽象出一元二次不等式的过程,体会学习本单元的意义;在自主探究与讨论交流过程中,培养学生的合作意识和创新精神。
教学重点
弄清一元二次不等式、一元二次方程、二次函数三者之间的关系,
掌握一元二次不等式的解法。
教学难点
一元二次不等式、一元二次方程、二次函数三个二次之间的关系及数形结合思想的渗透.
教学方法
发现式、探究式、互动讲解式教学法
通过“三个二次”关系的寻求,得到一元二次不等式的解.
学法指导
合作学习,自我练习,类比思考
教学过程
一、创设情景,得出一元二次不等式的定义
在一条限速为40km/h的城市公路上,一辆汽车发生交通事故,交警勘察发现该汽车刹车距离超过了20米,但未超过30米,通过分析交警很快得出该汽车在该路段时是否超速行驶。
已知该汽车刹车距离和行驶速度有以下函数关系s=0.01v2+0.1v请同学们根据实际情景建立对应关系。既20<0.01v2+0.1v≤30
形如 ax 2 +bx+c>0( ≥ 0) 或 ax 2 +bx+c<0( ≤ 0) 的不等式(其中 a ≠ 0 ),叫做 一元二次不等式
二、借助二次方程和二次函数图像探究一元二次不等式解法()
1.学生回忆二次方程ax 2+bx+c=0 解的情况
2.学生回忆()的图像形式
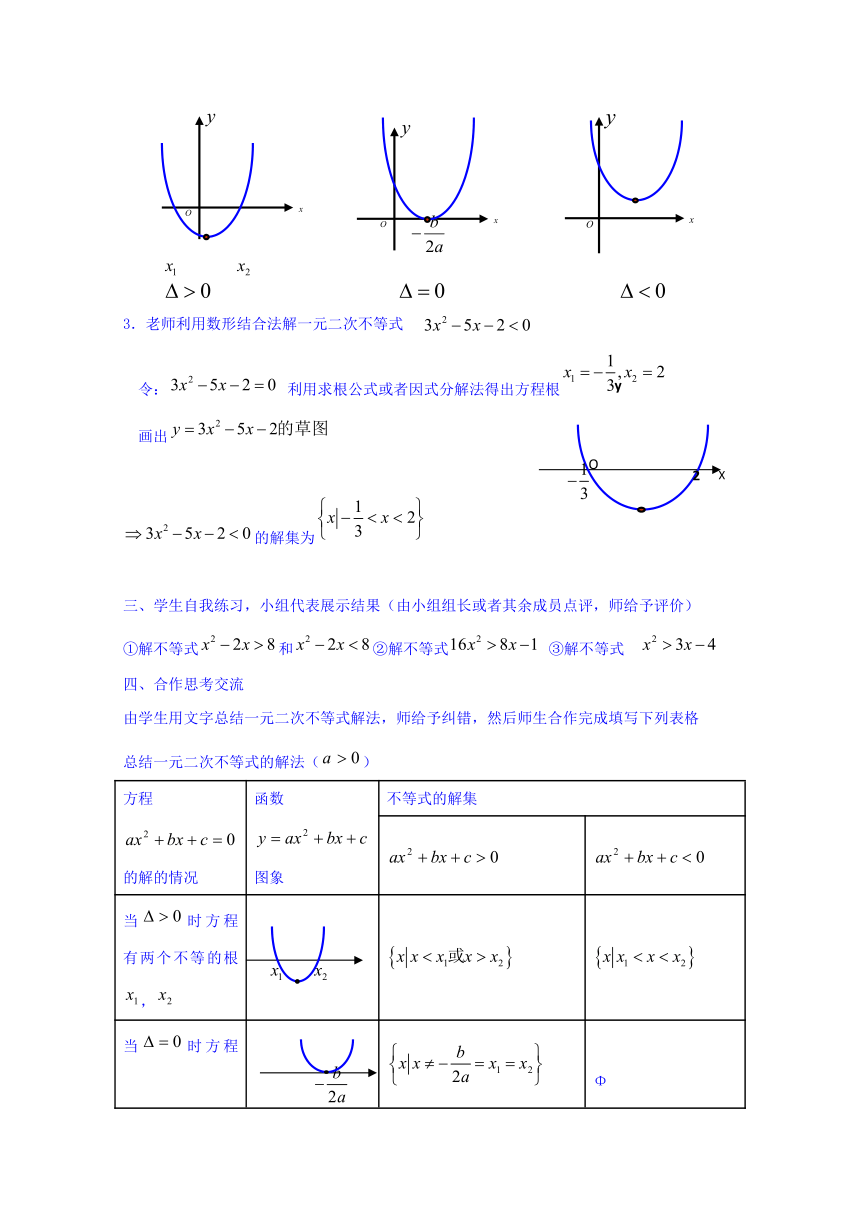
3.老师利用数形结合法解一元二次不等式
令: 利用求根公式或者因式分解法得出方程根
画出
的解集为
三、学生自我练习,小组代表展示结果(由小组组长或者其余成员点评,师给予评价)
①解不等式和②解不等式 ③解不等式
四、合作思考交流
由学生用文字总结一元二次不等式解法,师给予纠错,然后师生合作完成填写下列表格
总结一元二次不等式的解法()
方程
的解的情况
函数
图象
不等式的解集
当时方程有两个不等的根,
当时方程有一根
Φ
当时方程无实根
R
Φ
五、合作练习(学生抢答完成,师肯定与评价)
①已知函数的图象与轴的交点横坐标为和3,则时的取值集合为 ;当时的取值集合为 .
②若方程无实数根,则不等式的解集是 R .
③已知不等式<0 的解集是{ x︱},则 ,
六、回归情景问题:20<0.01v2+0.1v≤30学生完成求解并加以说明,谈对实际问题解决的体会。
课堂小结:(由学生完成,老师补充)
1.本节课我们学习了一个重要的解一元二次不等式的方法——数形结合
2.了解了一元二次不等式的一般式:
3.如果不是一般式的优先变为一般式;
4.根据判别式确定对应方程根的情况,并求出对应实数根;
5.由对应方程根的情况作出对应二次函数的图象;
6.据函数的图象写出不等式解的情况
板书设计:
课题
(一):一元二次不等式定义 (三):函数在图像(学生分组板书练习在另一个黑板展示)
(二):二次方程根的情况 (四):一元二次不等式解法
布置作业:P783和P877①②③
一元二次不等式的解法(1)学案简稿学习目标:
1.会从实际情境中抽象出一元二次不等式模型.
2.通过二次函数图像了解一元二次不等式与相应二次函数、一元二次方程的联系.
3.会利用二次函数图像求一元二次不等式的解集
达标过程:
情景问题:在一条限速为40km/h的城市公路上,一辆汽车发生交通事故,交警勘察发现该汽车刹车距离超过20米,但未超过30米,通过分析交警很快得出该汽车在该路段时是否超速行驶。(已知该汽车刹车距离和行驶速度有以下函数关系s=0.01v2+0.1v请同学们根据实际情景建立对应关系)
学生课堂自主完成并给出展示①解不等式和
②解不等式 ③解不等式
思考交流:完成表格填写(a>0)
方程
的解的情况
函数
图象
不等式的解集
当时方程有两个不等的根,
当时方程有一根
当时方程无实根
课堂合作练习①已知函数的图象与轴的交点横坐标为-2和3,则时的取值集合为 ;当时的取值集合为 .
②若方程无实数根,则不等式的解集是 .
③已知不等式<0 的解集是{ x︱},则
情景问题回归求解:20<0.01v2+0.1v≤30
学生小结反思:
教 学 反 思
------《一元二次不等式的解法》(1)
一、我对本节课的教学定位
由于一元二次不等式解法第一课时,作为不等式的一项重要内容,主要要达到的目标是让学生能熟练掌握一元二次不等式解法,理解一元二次方程、一元二次不等式和二次函数之间的关系。
并会用三者关系求解一元二次不等式解集。本节内容是不等式的重要部分,在高中数学教学内容和高考中,占据着比较重要的地位。在新的课程标准要求下,利用从实际情景中抽象出一元二次不等式的过程,让学生体会到学习本单元的意义,新的标准要求老师更要的要培养学生的自我创新意识和学生合作学习能力与自我学习能力的提升,所以,在整个过程中,更多的采用学生自我体会、训练、合作探究来完成。
二、教学思想方法的应用
本节数学思想方法分析:作为一名数学老师,不仅要传授给学生数学知识,更重要的是培养学生的数学思想,提升学生积极思维的数学意识;因此在本节课教学中我力求面向每个学生;充分将数形结合、函数、方程思想渗透到每个学生心里。在教学中,采用实例引入概念,结合图形,学生观察与合作探究、自我练习、合作练习完成本节课。
我们常说:“现代的文盲不是不识字的人,而是没有掌握学习方法的人”,由于我所面对的是我校高二年级普通班级的学生,学生整体水平一般,思维活跃程度不够,因而在教学中特别重视了学法的指导。采用图像法解题,让他们数形结合思想更加成熟,使学生的合作学习和实践应用能力得到了普遍提升。
三、教学设计反思
1.多媒体展示目标的过程,就是为了让每个学生在学习过程中始终了解到自己本节课要达到的目的是什么
2.利用二次函数图像导出解法,板书例题,主要是为了体现解法的标准格式和数形结合思想的形成。
3.学生自主练习设计为非一般形式,目的是进一步让学生熟悉在解不等式问题时要先将不等式化简为一般形式,也为下节课学习二次项系数为负数的变形打下基础,同时,在小组自我评价过程中让学生自我感受到进步的喜悦。还有,在学生练习中的巡视和指导,主要是面对学生比较有困难的学生,促进他们同时进步。
4.后面的填表采用合作交流,兵教兵的方式实现,主要是为了使每个学生都能充分理解三个二次之间的关系,但是由于学生之间的差异,有个别学生完成的不是很好,在后面的教学中,我还要更加关注这些学生。
5.背景问题解决,起到前后对应的效果,体现学以致用。
四、教学效果和板书设计反思
从本节课效果来看,达到了自己预期的目的,实现了新课程下学生基本能力的培养的数学能力与思想的形成。但是,在分层达标的知识扩展上还做的不够,自己将在后面的教学中,结合学生差异,加大分层达标力度,提升不同层次效果。由于本节课重点是一元二次不等式解法,所以,在板书设计上,除过板书定义之外,对于利用二次方程和二次函数求解二次不等式的求解过程将严格板书,同时,通过图表的板书让学生进一步理解三个二次之间的关系。
在本节课里,为了让学生更清晰的认识本节课要完成的目标,将目标开始后展示在多媒体屏幕上,长时间展现在学生面前。同时,为了学生能更好完成本届目标,将教材例题坐了同等水平改编,主要是为了加大学生对知识和方法的理解和运用;为了加深学生对本节内容的理解,将图表采用动画的形式在学生的回答中展示在多媒体上,让每个学生都进一步理解基本解法,最后,将课堂小结的内容用PPT展示给学生,起到提升课堂效果的作用。
教学目标
(一)知识目标:熟练掌握一元二次不等式解法,理解一元二次方程、一元二次不等式和二次函数之间的关系。
(二)能力目标:培养学生运用等价转化和数形结合等数学思想解决数学问题的能力。
(三)情感目标:通过等与不等的对立统一关系的认识,对学生进行辩证唯物主义教育;经历从实际情景中抽象出一元二次不等式的过程,体会学习本单元的意义;在自主探究与讨论交流过程中,培养学生的合作意识和创新精神。
教学重点
弄清一元二次不等式、一元二次方程、二次函数三者之间的关系,
掌握一元二次不等式的解法。
教学难点
一元二次不等式、一元二次方程、二次函数三个二次之间的关系及数形结合思想的渗透.
教学方法
发现式、探究式、互动讲解式教学法
通过“三个二次”关系的寻求,得到一元二次不等式的解.
学法指导
合作学习,自我练习,类比思考
教学过程
一、创设情景,得出一元二次不等式的定义
在一条限速为40km/h的城市公路上,一辆汽车发生交通事故,交警勘察发现该汽车刹车距离超过了20米,但未超过30米,通过分析交警很快得出该汽车在该路段时是否超速行驶。
已知该汽车刹车距离和行驶速度有以下函数关系s=0.01v2+0.1v请同学们根据实际情景建立对应关系。既20<0.01v2+0.1v≤30
形如 ax 2 +bx+c>0( ≥ 0) 或 ax 2 +bx+c<0( ≤ 0) 的不等式(其中 a ≠ 0 ),叫做 一元二次不等式
二、借助二次方程和二次函数图像探究一元二次不等式解法()
1.学生回忆二次方程ax 2+bx+c=0 解的情况
2.学生回忆()的图像形式
3.老师利用数形结合法解一元二次不等式
令: 利用求根公式或者因式分解法得出方程根
画出
的解集为
三、学生自我练习,小组代表展示结果(由小组组长或者其余成员点评,师给予评价)
①解不等式和②解不等式 ③解不等式
四、合作思考交流
由学生用文字总结一元二次不等式解法,师给予纠错,然后师生合作完成填写下列表格
总结一元二次不等式的解法()
方程
的解的情况
函数
图象
不等式的解集
当时方程有两个不等的根,
当时方程有一根
Φ
当时方程无实根
R
Φ
五、合作练习(学生抢答完成,师肯定与评价)
①已知函数的图象与轴的交点横坐标为和3,则时的取值集合为 ;当时的取值集合为 .
②若方程无实数根,则不等式的解集是 R .
③已知不等式<0 的解集是{ x︱},则 ,
六、回归情景问题:20<0.01v2+0.1v≤30学生完成求解并加以说明,谈对实际问题解决的体会。
课堂小结:(由学生完成,老师补充)
1.本节课我们学习了一个重要的解一元二次不等式的方法——数形结合
2.了解了一元二次不等式的一般式:
3.如果不是一般式的优先变为一般式;
4.根据判别式确定对应方程根的情况,并求出对应实数根;
5.由对应方程根的情况作出对应二次函数的图象;
6.据函数的图象写出不等式解的情况
板书设计:
课题
(一):一元二次不等式定义 (三):函数在图像(学生分组板书练习在另一个黑板展示)
(二):二次方程根的情况 (四):一元二次不等式解法
布置作业:P783和P877①②③
一元二次不等式的解法(1)学案简稿学习目标:
1.会从实际情境中抽象出一元二次不等式模型.
2.通过二次函数图像了解一元二次不等式与相应二次函数、一元二次方程的联系.
3.会利用二次函数图像求一元二次不等式的解集
达标过程:
情景问题:在一条限速为40km/h的城市公路上,一辆汽车发生交通事故,交警勘察发现该汽车刹车距离超过20米,但未超过30米,通过分析交警很快得出该汽车在该路段时是否超速行驶。(已知该汽车刹车距离和行驶速度有以下函数关系s=0.01v2+0.1v请同学们根据实际情景建立对应关系)
学生课堂自主完成并给出展示①解不等式和
②解不等式 ③解不等式
思考交流:完成表格填写(a>0)
方程
的解的情况
函数
图象
不等式的解集
当时方程有两个不等的根,
当时方程有一根
当时方程无实根
课堂合作练习①已知函数的图象与轴的交点横坐标为-2和3,则时的取值集合为 ;当时的取值集合为 .
②若方程无实数根,则不等式的解集是 .
③已知不等式<0 的解集是{ x︱},则
情景问题回归求解:20<0.01v2+0.1v≤30
学生小结反思:
教 学 反 思
------《一元二次不等式的解法》(1)
一、我对本节课的教学定位
由于一元二次不等式解法第一课时,作为不等式的一项重要内容,主要要达到的目标是让学生能熟练掌握一元二次不等式解法,理解一元二次方程、一元二次不等式和二次函数之间的关系。
并会用三者关系求解一元二次不等式解集。本节内容是不等式的重要部分,在高中数学教学内容和高考中,占据着比较重要的地位。在新的课程标准要求下,利用从实际情景中抽象出一元二次不等式的过程,让学生体会到学习本单元的意义,新的标准要求老师更要的要培养学生的自我创新意识和学生合作学习能力与自我学习能力的提升,所以,在整个过程中,更多的采用学生自我体会、训练、合作探究来完成。
二、教学思想方法的应用
本节数学思想方法分析:作为一名数学老师,不仅要传授给学生数学知识,更重要的是培养学生的数学思想,提升学生积极思维的数学意识;因此在本节课教学中我力求面向每个学生;充分将数形结合、函数、方程思想渗透到每个学生心里。在教学中,采用实例引入概念,结合图形,学生观察与合作探究、自我练习、合作练习完成本节课。
我们常说:“现代的文盲不是不识字的人,而是没有掌握学习方法的人”,由于我所面对的是我校高二年级普通班级的学生,学生整体水平一般,思维活跃程度不够,因而在教学中特别重视了学法的指导。采用图像法解题,让他们数形结合思想更加成熟,使学生的合作学习和实践应用能力得到了普遍提升。
三、教学设计反思
1.多媒体展示目标的过程,就是为了让每个学生在学习过程中始终了解到自己本节课要达到的目的是什么
2.利用二次函数图像导出解法,板书例题,主要是为了体现解法的标准格式和数形结合思想的形成。
3.学生自主练习设计为非一般形式,目的是进一步让学生熟悉在解不等式问题时要先将不等式化简为一般形式,也为下节课学习二次项系数为负数的变形打下基础,同时,在小组自我评价过程中让学生自我感受到进步的喜悦。还有,在学生练习中的巡视和指导,主要是面对学生比较有困难的学生,促进他们同时进步。
4.后面的填表采用合作交流,兵教兵的方式实现,主要是为了使每个学生都能充分理解三个二次之间的关系,但是由于学生之间的差异,有个别学生完成的不是很好,在后面的教学中,我还要更加关注这些学生。
5.背景问题解决,起到前后对应的效果,体现学以致用。
四、教学效果和板书设计反思
从本节课效果来看,达到了自己预期的目的,实现了新课程下学生基本能力的培养的数学能力与思想的形成。但是,在分层达标的知识扩展上还做的不够,自己将在后面的教学中,结合学生差异,加大分层达标力度,提升不同层次效果。由于本节课重点是一元二次不等式解法,所以,在板书设计上,除过板书定义之外,对于利用二次方程和二次函数求解二次不等式的求解过程将严格板书,同时,通过图表的板书让学生进一步理解三个二次之间的关系。
在本节课里,为了让学生更清晰的认识本节课要完成的目标,将目标开始后展示在多媒体屏幕上,长时间展现在学生面前。同时,为了学生能更好完成本届目标,将教材例题坐了同等水平改编,主要是为了加大学生对知识和方法的理解和运用;为了加深学生对本节内容的理解,将图表采用动画的形式在学生的回答中展示在多媒体上,让每个学生都进一步理解基本解法,最后,将课堂小结的内容用PPT展示给学生,起到提升课堂效果的作用。
