12.2 第4课时 利用“HL”判定直角三角形全等 习题课件
文档属性
| 名称 | 12.2 第4课时 利用“HL”判定直角三角形全等 习题课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 16:11:37 | ||
图片预览




文档简介
(共24张PPT)
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
己7世纪盲
27世纪数
UUU2ICnY.C
aC
oab
e m
d
27世自
第4课时利用“HI”判定直角三角形全等
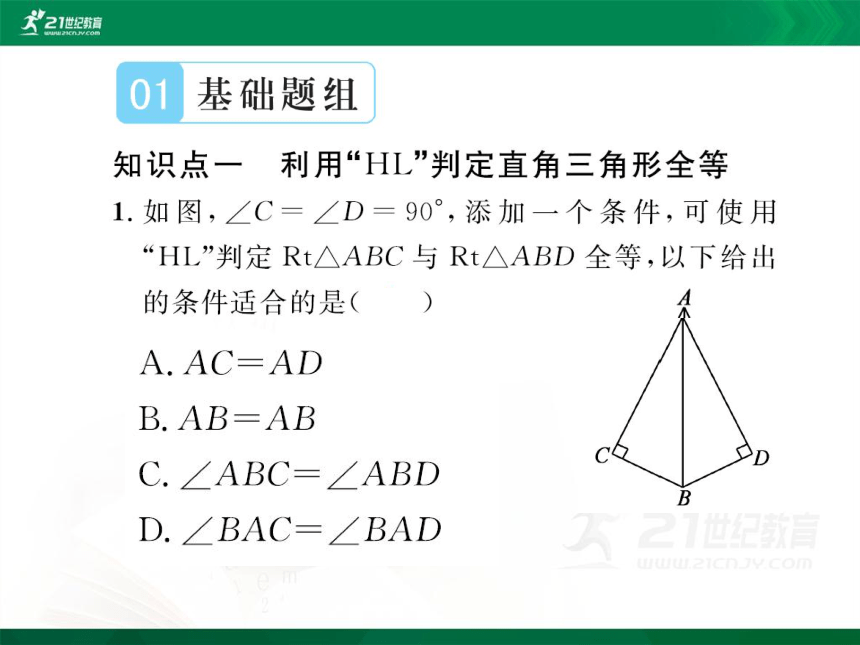
A AC=AD
B AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
C
D
B
01基础题组
知识点一利用“H”判定直角三角形全等
1.如图,∠C=∠D=90°,添加一个条件,可使用
“HL”判定Rt△ABC与Rt△ABD全等,以下给出
的条件适合的是(A)
2.下列条件:①两条直角边对应相等;②斜边和一锐
角对应相等;③斜边和一直角边对应相等;④直角
边和一锐角对应相等.以上能判定两直角三角形全
等的个数有(D)
A.1个B.2个C.3个D.4个
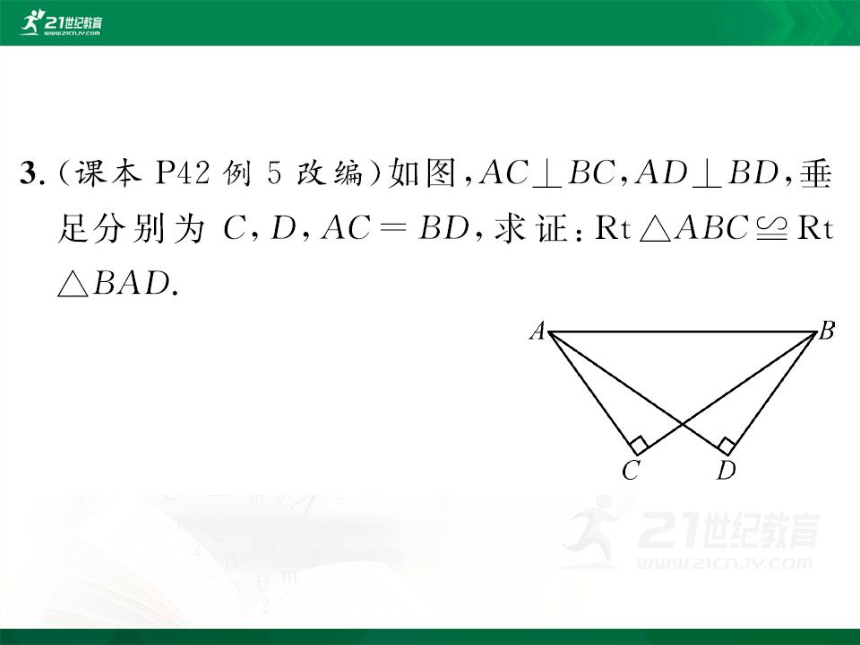
3.(课本P42例5改编)如图,AC⊥BC,AD⊥BD,垂
足分别为C,D,AC=BD,求证:Rt△ABC≌Rt
BaD
B
D
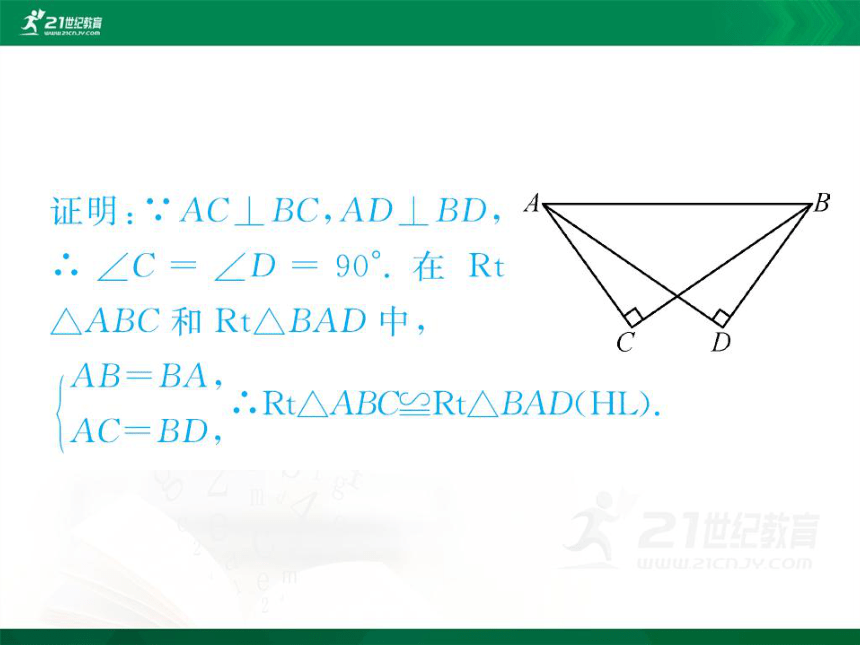
证明:∵AC⊥BC,AD⊥BD,A
B
∠C=∠D=90°.在Rt
△ABC和Rt△BAD中,
D
AB=BA
Rt△ABC≌Rt△BAD(HL)
AC-BD,
4.(2018~2019·广安期中)如图,已知AB=CD,
BE=DF,∠A=∠C=90°,求证:AB∥CD
证明:∴BE=DF,BE+EF=
DF+EF,∴BF=DE.在
Rt△ABF和Rt△CDE中,BE
D
F
AB=CD,
Rt△ABF≌Rt
BF=DE
△CDE(HL),∴∠B=∠D,,AB∥CD
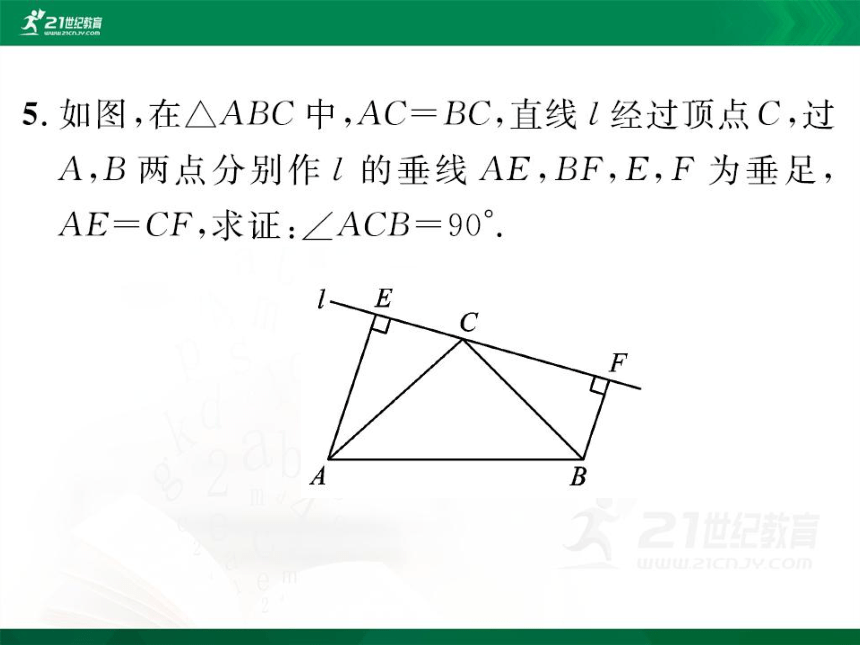
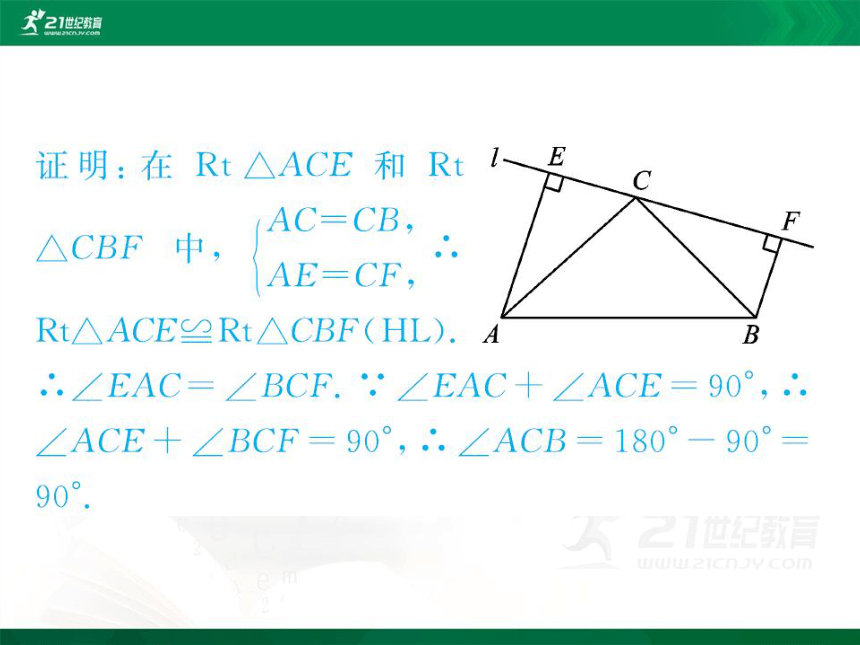
5.如图,在△ABC中,AC=BC,直线l经过顶点C,过
A,B两点分别作l的垂线AE,BF,E,F为垂足,
AE=CF,求证:∠ACB=90°
- E
B
证明:在Rt△ACE和Rt1-B
AC= CB
△CBF中
AE=CF
Rt△ACE≌Rt△CBF(HL).A
B
∠EAC=∠BCF.∵∠EAC+∠ACE=90°,
∠ACE+∠BCF=90°,∴∠ACB=180°-90
90
知识点二直角三角形全等判定的灵活运用
6.如图,AB⊥CF于点B,AD⊥CE于点D,且AB=
AD,DE=BF,求证:AF=AE
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
己7世纪盲
27世纪数
UUU2ICnY.C
aC
oab
e m
d
27世自
第4课时利用“HI”判定直角三角形全等
A AC=AD
B AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
C
D
B
01基础题组
知识点一利用“H”判定直角三角形全等
1.如图,∠C=∠D=90°,添加一个条件,可使用
“HL”判定Rt△ABC与Rt△ABD全等,以下给出
的条件适合的是(A)
2.下列条件:①两条直角边对应相等;②斜边和一锐
角对应相等;③斜边和一直角边对应相等;④直角
边和一锐角对应相等.以上能判定两直角三角形全
等的个数有(D)
A.1个B.2个C.3个D.4个
3.(课本P42例5改编)如图,AC⊥BC,AD⊥BD,垂
足分别为C,D,AC=BD,求证:Rt△ABC≌Rt
BaD
B
D
证明:∵AC⊥BC,AD⊥BD,A
B
∠C=∠D=90°.在Rt
△ABC和Rt△BAD中,
D
AB=BA
Rt△ABC≌Rt△BAD(HL)
AC-BD,
4.(2018~2019·广安期中)如图,已知AB=CD,
BE=DF,∠A=∠C=90°,求证:AB∥CD
证明:∴BE=DF,BE+EF=
DF+EF,∴BF=DE.在
Rt△ABF和Rt△CDE中,BE
D
F
AB=CD,
Rt△ABF≌Rt
BF=DE
△CDE(HL),∴∠B=∠D,,AB∥CD
5.如图,在△ABC中,AC=BC,直线l经过顶点C,过
A,B两点分别作l的垂线AE,BF,E,F为垂足,
AE=CF,求证:∠ACB=90°
- E
B
证明:在Rt△ACE和Rt1-B
AC= CB
△CBF中
AE=CF
Rt△ACE≌Rt△CBF(HL).A
B
∠EAC=∠BCF.∵∠EAC+∠ACE=90°,
∠ACE+∠BCF=90°,∴∠ACB=180°-90
90
知识点二直角三角形全等判定的灵活运用
6.如图,AB⊥CF于点B,AD⊥CE于点D,且AB=
AD,DE=BF,求证:AF=AE
