北师大版中考总复习资料:25投影与视图(附答案)
文档属性
| 名称 | 北师大版中考总复习资料:25投影与视图(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 695.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-27 16:43:49 | ||
图片预览


文档简介
中考总复习:投影与视图—知识讲解
【考纲要求】
1.通过实例了解平行投影和中心投影的含义及简单应用;
2.会画基本几何体(直棱柱、圆柱、圆锥、球)的三视图(主视图,左视图、俯视图),能根据三视图描述基本几何体或实物的原型.
【知识网络】
【考点梳理】
考点一、生活中的几何体
1.常见的几何体的分类
在丰富多彩的图形世界中,我们常见的几何体有长方体、正方体、棱柱体、棱锥体、圆柱体、圆锥体、球体、台体等.
2.点、线、面、体的关系
(1)点动成线,线动成面,面动成体;
(2)面面相交成线,线线相交成点.
要点诠释:体体相交可成点,不一定成线.
3.基本几何体的展开图
(1)正方体的展开图是六个正方形;
(2)棱柱的展开图是两个多边形和一个长方形;
(3)圆锥的展开图是一个圆和一个扇形;
(4)圆柱的展开图是两个圆和一个长方形.
考点二、投影
1.投影
用光线照射物体,在某个平面上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在平面叫做投影面.
2.平行投影和中心投影
由平行光线形成的投影是平行投影;由同一点(点光源)发出的光线形成的投影叫做中心投影.
3.正投影
投影线垂直投影面产生的投影叫做正投影.
要点诠释:正投影是平行投影的一种.
考点三、物体的三视图
1.物体的视图
当我们从某一角度观察一个物体时,所看到的图象叫做物体的视图.
我们用三个互相垂直的平面作为投影面,其中正对我们的叫做正面,正面下方的叫做水平面,右边的叫做侧面.
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.
要点诠释:三视图就是我们从三个方向看物体所得到的3个图象.
2.画三视图的要求
(1)位置的规定:主视图下方是俯视图,主视图右边是左视图.
(2)长度的规定:长对正,高平齐,宽相等.
要点诠释:主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.
【典型例题】
类型一、三视图及展开图
1.用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
A.22 B.19 C.16 D.13
【思路点拨】视图、俯视图是分别从物体正面、上面看,所得到的图形.
【答案】D;
【解析】综合主视图和俯视图,这个几何体的底层最少有3+3+1=7个小正方体,第二层最少有3个,
第三层最少有2个,第四层最少有1个,因此搭成这样的一个几何体至少需要小正方体木块的个数为:7+3+2+1=13个.故答案为:13.
【总结升华】由三视图判断组成原几何体的小正方体的个数与由相同的小正方体构成的几何体画三视图正好相反.
举一反三:
【变式1】如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是________.
【答案】6.
【高清课堂:《空间与图形》专题:投影与视图 例6】
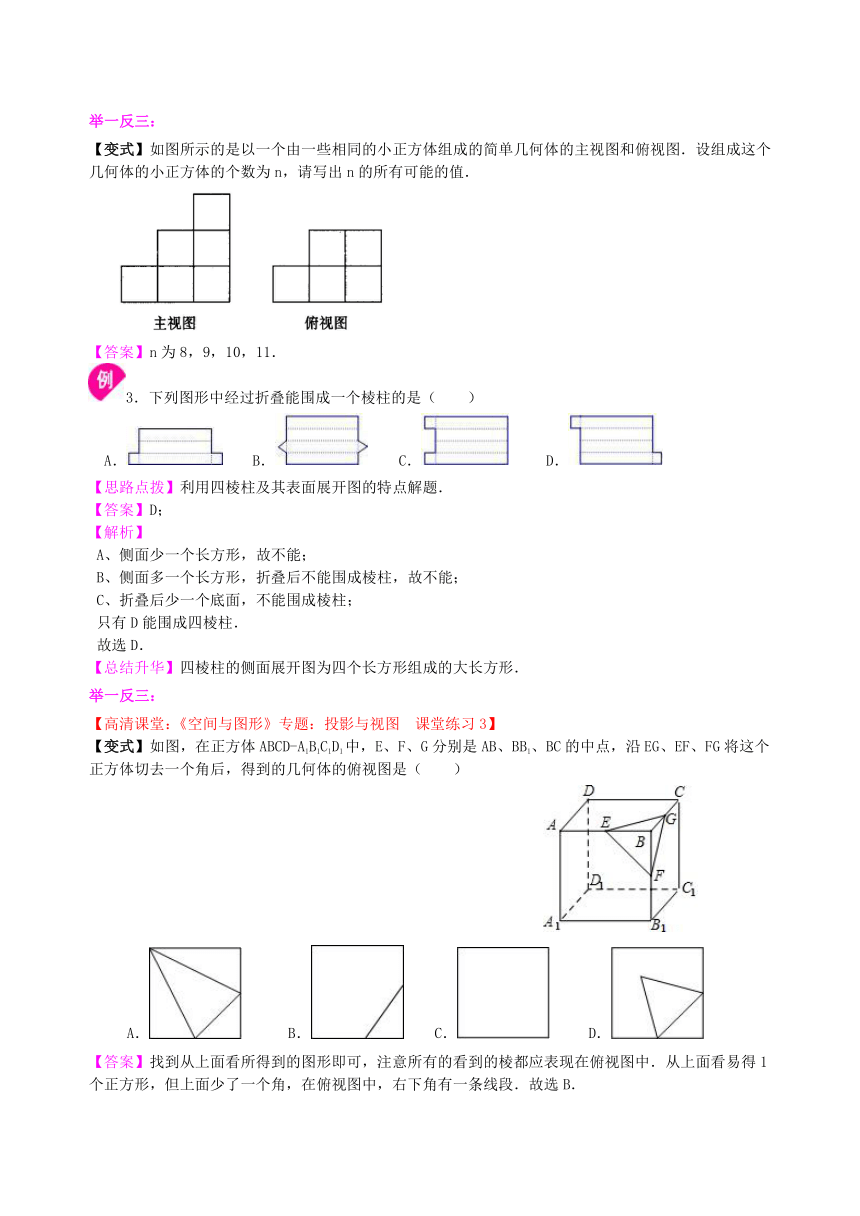
【变式2】下图是由几个相同的小正方体搭成的几何体从三个方向看到的图形,则搭成这个几何体的小正方体的个数是( )个.
A.5 B.6 C.7 D.8
【答案】B.
2.美术课上,老师要求同学们将如图所示的白纸只沿虚线剪开,用裁开的纸片和白纸上的阴影部份围成一个立体模型,然后放在桌面上,下面四个示意图中,只有一个符合上述要求,那么这个示意图是( )
A. B.
C. D.
【思路点拨】动手操作看得到小正方体的阴影部分的具体部位即可.
【答案】B
【解析】动手操作折叠成正方体的形状放置到白纸的阴影部分上,所得正方体中的阴影部分应紧靠白纸, 故选B.
【总结升华】用到的知识与正方体展开图有关,考察学生空间想象能力.建议学生在平时的教学过程中应结合实际模型将展开图的若干种情况分析清楚.
举一反三:
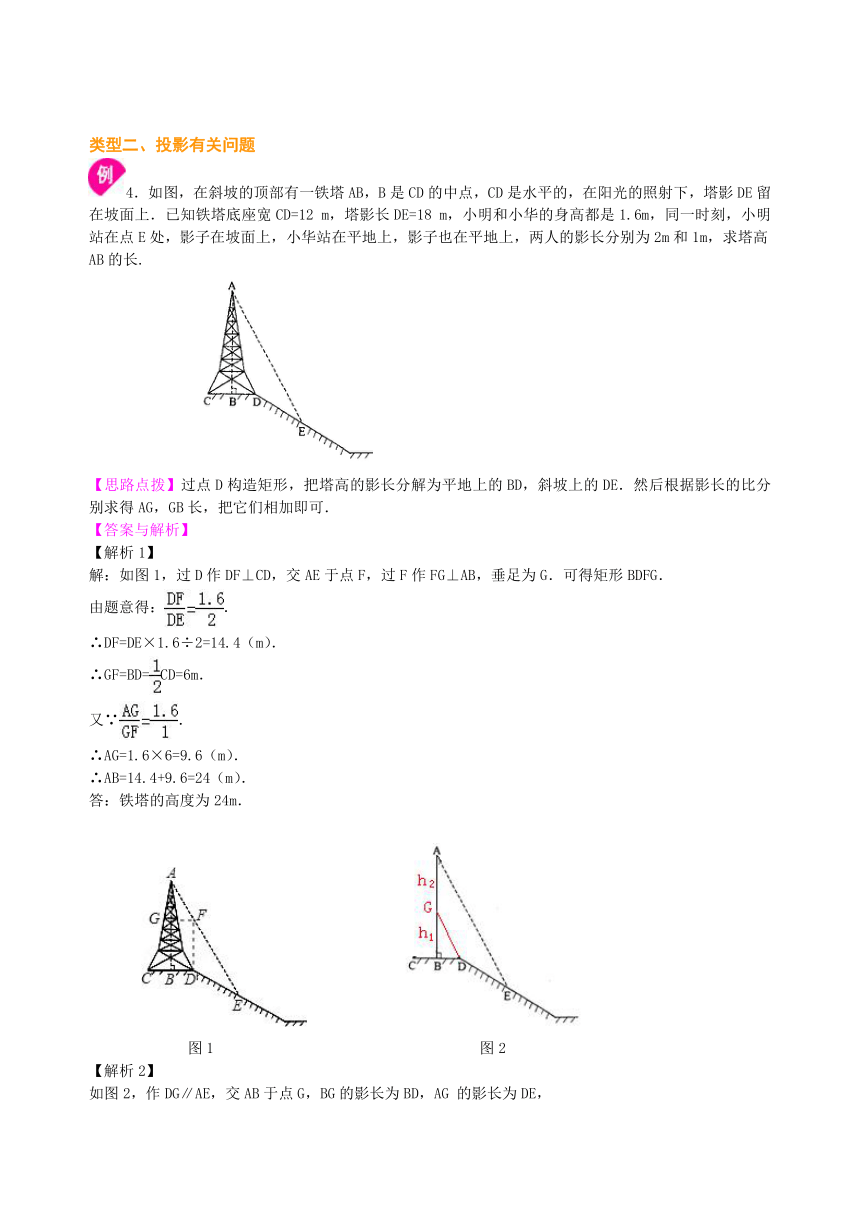
【变式】如图所示的是以一个由一些相同的小正方体组成的简单几何体的主视图和俯视图.设组成这个几何体的小正方体的个数为n,请写出n的所有可能的值.
【答案】n为8,9,10,11.
3.下列图形中经过折叠能围成一个棱柱的是( )
A. B. C. D.
【思路点拨】利用四棱柱及其表面展开图的特点解题.
【答案】D;
【解析】
A、侧面少一个长方形,故不能; B、侧面多一个长方形,折叠后不能围成棱柱,故不能; C、折叠后少一个底面,不能围成棱柱; 只有D能围成四棱柱. 故选D.
【总结升华】四棱柱的侧面展开图为四个长方形组成的大长方形.
举一反三:
【高清课堂:《空间与图形》专题:投影与视图 课堂练习3】
【变式】如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AB、BB1、BC的中点,沿EG、EF、FG将这个正方体切去一个角后,得到的几何体的俯视图是( )
A. B. C. D.
【答案】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.从上面看易得1个正方形,但上面少了一个角,在俯视图中,右下角有一条线段.故选B.
类型二、投影有关问题
4.如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,求塔高AB的长.
【思路点拨】过点D构造矩形,把塔高的影长分解为平地上的BD,斜坡上的DE.然后根据影长的比分别求得AG,GB长,把它们相加即可.
【答案与解析】
【解析1】
解:如图1,过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.可得矩形BDFG.
由题意得:.
∴DF=DE×1.6÷2=14.4(m).
∴GF=BD=CD=6m.
又∵.
∴AG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m.
图1 图2
【解析2】
如图2,作DG∥AE,交AB于点G,BG的影长为BD,AG 的影长为DE,
由题意得:.
∴AG=18×1.6÷2=14.4(m).
又∵.
∴BG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m.
【总结升华】运用所学的解直角三角形的知识解决实际生活中的问题,要求我们要具备数学建模能力(即将实际问题转化为数学问题).
类型三、投影视图综合问题
5.用小立方体搭成一个几何体,使它的主视图和俯视图如图所示,搭建这样的几何体最多要 小立方体.
【思路点拨】从正视图和侧视图考查几何体的形状,从俯视图看出几何体的小立方块最多的数目.
【答案】17.
【解析】
解:由主视图可知,它自下而上共有3列,第一列3块,第二列2块,第三列1块. 由俯视图可知,它自左而右共有3列,第二列各3块,第三列1块,从空中俯视的块数只要最低层有一块即可.因此,综合两图可知这个几何体的形状不能确定;如图,最多时有3×5+2×1=17块小立方体. 故答案为17.
【总结升华】本题考查简单空间图形的三视图,考查空间想象能力,是基础题,但很容易出错.
6.太阳光线与水平线的夹角在新疆地区的变化较大,夏至时夹角最大,冬至时夹角最小,最小夹角约为28度.现有两幢居民住宅楼高为15米,两楼相距20米,如图所示. (1)在冬至时,甲楼的影子在乙楼上有多高? (2)若在本小区内继续兴建同样高的住宅楼,楼距至少应该多少米,才不影响楼房的采光?(前一幢楼房的影子不能落在后一幢楼房上)(计算结果精确到0.1米)
【思路点拨】
(1)如图,构造直角三角形ADE,则∠ADE=28°,DE=BC=20,在这个三角形中已知一边和一个锐角,满足解直角三角形的条件,可求出AE的长从而求得CD的长. (2)在△ABC中,由角C的值和AB的高,满足解直角三角形的条件,可求出BC的长.
【答案与解析】
解:(1)如图所示, 作DE⊥AB,垂足为E, 由题意可知∠ADE=28°,DE=BC=20, 在Rt△ADE中,tan∠ADE= , AE=DE?tan∠DAE=20?tan28°≈10.6, 则DC=EB=AB-AE=15-10.6=4.4. 即冬至时甲楼的影子在乙楼上约4.4米高. (2)若要不影响要房间的采光,如图所示在Rt△ABC中,AB=15,∠C=28°, BC= .
答:楼距至少28.2米,才不影响楼房的采光.
【总结升华】本题是解直角三角形在生活中的实际应用,做到学数学,用数学,才是学习数学的意义.
7.如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过底面圆的圆心,其高 m,底面半径为2m.某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4m. (1)求∠B的度数; (2)若∠ACP=2∠B,求光源A距平面的高度.
【思路点拨】
(1)如下图所示,过点D作DF垂直BC于点F.由题意,得DF= ,EF=2,BE=4,在Rt△DFB中,tan∠B= ,由此可以求出∠B;
(2)过点A作AH垂直BP于点H.因为∠ACP=2∠B=60°所以∠BAC=30°,AC=BC=8.在Rt△ACH中,AH=AC?Sin∠ACP,所以可以求出AH了,即求出了光源A距平面的高度.
【答案与解析】
解:(1)过点D作DF垂直BC于点F. 由题意,得DF=,EF=2,BE=4. 在Rt△DFB中,tan∠B=, 所以∠B=30°; (2)过点A作AH垂直BP于点H. ∵∠ACP=2∠B=60°, ∴∠BAC=30°, ∴AC=BC=8, 在Rt△ACH中,AH=AC?Sin∠ACP=,
即光源A距平面的高度为m.
【总结升华】
本题考查了学生运用三角函数知识解决实际问题的能力,又让学生感受到生活处处有数学,数学在生产生活中有着广泛的作用.
中考总复习:投影与视图—巩固练习
【巩固练习】
一、选择题 1.如图所示的一组几何体的俯视图是( )
2.如图,形状相同、大小相等的两个小木块放在一起,其俯视图如图所示,则其主视图是( )
3.如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为( )
4.如图是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A. B. C. D.
5.如图,是由若干个同样大小的立方体搭成的几何体的俯视图,小正方形中的数字表示该位置立方体的个数,则这个几何体的主视图是( )
6.如图是一个包装纸盒的三视图(单位:cm),则制作一个纸盒所需纸板的面积是( )
A. B. C. D.
二、填空题
7.长方体的主视图与俯视图如图所示,则这个长方体的体积是 .
8.如图,上体育课,甲、乙两名同学分别站在C,D的位置时,乙的影子恰好在甲的影子里边,已知甲、乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是_________米.
第7题 第8题 第9题 第10题
9.如图,小明在A时测得某树影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为________m.
10.如图是由大小相同的小正方体组成的简单几何体的主视图和左视图,那么组成这个几何体的小正方体的个数最多为__________.
11.如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是_________.
12.如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕点A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设垂直于地面时的影长为AC(假定AC>AB),影长的最大值为m,最小值为n,那么下列结论:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小,其中正确结论的序号是___ _____.
三、解答题
13.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,求其影子B1C1的长;当小明继续走剩下路程的到B2处时,求其影子B2C2的长;当小明继续走剩下路程的到B3处,……按此规律继续走下去,当小明走剩下路程的到Bn处时,其影子的长为________m(直接用含n的代数式表示).
14. 如图,某居民小区内A、B两楼之间的距离MN=30m,两楼的高都是20m,A楼在B楼正南,B楼窗户朝南.B楼内一楼住户的窗台离小区地面的距离DN=2m,窗户高CD=1.8m.当正午时刻太阳光线与地面成30°角时,A楼的影子是否影响B楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.(参考数据:=1.414,=1.732,=2.236)
15.某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°角.(≈1.4,≈1.7)
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.(用图(2)解答)
①求树与地面成45°角时的影长;
②求树的最大影长.
16..如图(1)是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形,现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图(2)),然后用这条平行四边形纸带按如图(3)的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图(2)中,计算裁剪的角度∠BAD;
(2)计算按图(3)方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
【答案与解析】
一、选择题 1.【答案】B;
【解析】圆锥的俯视图是带圆心的圆,六棱柱的俯视图是正六边形,所以它们的俯视图是B.
2.【答案】D;
【解析】只有D答案体现了后排只有一层.
3.【答案】A;
【解析】根据中心投影的性质,小亮的影长y随x逐渐变小再逐渐变大,且y是x的一次函数.
4.【答案】B;
【解析】该几何体是底面圆直径为a,母线长为c的圆锥,其侧面积.
5.【答案】D;
【解析】根据俯视图可知主视图有两列,左边一列的最大高度为2,右边一列的高度是3,故选D.
6.【答案】C;
【解析】由三视图知此包装纸盒是一个正六棱柱,其全面积
.
二、填空题
7.【答案】24;
【解析】由主视图和俯视图知长方体的长宽高分别为4,2,3,所以V=4×2×3=24.
8.【答案】6;
【解析】设甲的影长AC=x米,则乙的影长AD=(x-1)米.根据同一时刻物高与影长成比例,
可得.解得x=6(米).
9.【答案】4;
【解析】如图,设树高CD=h,在Rt△CEF中,由题意得ED=2,FD=8.由Rt△CDE∽△RFCD,
可得.即.∴ CD2=16.故CD=4m.即树的高度为4m.
10.【答案】7:
【解析】由主视图知几何体左右共两排,由左视图知几何体前后三排,且左排最高两层,所以组成这个几何体的小正方体的个数最多为7个.
11.【答案】6;
【解析】主视图能反映每一列的最大高度,左视图能反映每一行的最大高度,俯视图能反映行列数,由三视图可发现俯视图中行列的高度如图所示,则图中棱长为1的正方体的个数
是1+1+1+1+2=6(个).
12.【答案】①③④ ;
【解析】如图所示.当AB转至AE时影长最大值m=AD>AC,当AB转至AB′时影长最小值;
当AB转至AB′时影长最小值n=AB,影子的长度先增大后减小,所以正确结论的
序号是①③④.
三、解答题
13.【答案与解析】
解:(1)如图:
(2)由题意得△ABC∽△GHC.
∴.
∴.
∴GH=4.8m.
(3)∵△A1B1C1∽△GHC1,
∴.设B1C1长为xm,
则.解得,即B1C1=.
同理,解得,.
14.【答案与解析】
解:如图,设光线FE影响到B楼的E处,作EG⊥FM于点G,由题知,EG=MN=30m,∠FEG=30°.
则FG=30°×tan30°=30×==17.32 (m),
MG=FM-GF=20-17.32=2.68-2=0.68(m).因为DN=2m,CD=1.8m,
所以ED=2.68-2=0.68(m),即A楼影子影响到B楼一楼采光,挡住该户窗户0.68m.
15.【答案与解析】
解:(1)AB=ACtan30°=12×≈7(米).(结果也可以保留一位小数,下同)
答:树高约7米.
(2) 解析:①在Rt△ABC中,AB=ACtan30°;②过B1作B1N⊥AC1,在Rt△AB1N和Rt△B1NC1中分别求AN和NC1.当树与地面成60°角时影长最大(如图AC2)
①如图,B1N=AN=ABsin 45°=≈5(米).NC1=NB1tan60°=≈8(米).
AC1=AN+NC1=5+8≈13(米).
答:树与地面成45°角时影长为13米.
②如图,当树与地面成60°角时影长最大,为AC2=2AB2≈14(米)(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
16.【答案与解析】
解析:(1)观察图(3)的包贴方式知AB的长等于三棱柱的底面周长,
则AB=30.由AM=15可以求出∠ABM=30°.
由AD∥BC求出∠BAD=∠ABM=30°.
(2)可将三棱柱的侧面展开,利用平面图形计算MC的长.
解:(1)由图(3)的包贴方法知:AB的长等于三棱柱的底面周长,
∴AB=30.
∵纸带宽为15,sin∠DAB=sin∠ABM=,
∴∠DAB=30°.
(2)在图(3)中,将三棱柱沿过点A的侧棱剪开,得到如图甲的侧面展开图,
将图甲中的△ABE向左平移30 cm,△CDF向右平移30 cm,拼成如图乙中的平行四边形ABCD,
此平行四边形即为图(2)中的平行四边形ABCD.
由题意,知:BC=BE+CE=2CE=2×,
∴所需矩形纸带的长为MB+BC=30·cos30°+(cm).
【考纲要求】
1.通过实例了解平行投影和中心投影的含义及简单应用;
2.会画基本几何体(直棱柱、圆柱、圆锥、球)的三视图(主视图,左视图、俯视图),能根据三视图描述基本几何体或实物的原型.
【知识网络】
【考点梳理】
考点一、生活中的几何体
1.常见的几何体的分类
在丰富多彩的图形世界中,我们常见的几何体有长方体、正方体、棱柱体、棱锥体、圆柱体、圆锥体、球体、台体等.
2.点、线、面、体的关系
(1)点动成线,线动成面,面动成体;
(2)面面相交成线,线线相交成点.
要点诠释:体体相交可成点,不一定成线.
3.基本几何体的展开图
(1)正方体的展开图是六个正方形;
(2)棱柱的展开图是两个多边形和一个长方形;
(3)圆锥的展开图是一个圆和一个扇形;
(4)圆柱的展开图是两个圆和一个长方形.
考点二、投影
1.投影
用光线照射物体,在某个平面上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在平面叫做投影面.
2.平行投影和中心投影
由平行光线形成的投影是平行投影;由同一点(点光源)发出的光线形成的投影叫做中心投影.
3.正投影
投影线垂直投影面产生的投影叫做正投影.
要点诠释:正投影是平行投影的一种.
考点三、物体的三视图
1.物体的视图
当我们从某一角度观察一个物体时,所看到的图象叫做物体的视图.
我们用三个互相垂直的平面作为投影面,其中正对我们的叫做正面,正面下方的叫做水平面,右边的叫做侧面.
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.
要点诠释:三视图就是我们从三个方向看物体所得到的3个图象.
2.画三视图的要求
(1)位置的规定:主视图下方是俯视图,主视图右边是左视图.
(2)长度的规定:长对正,高平齐,宽相等.
要点诠释:主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.
【典型例题】
类型一、三视图及展开图
1.用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
A.22 B.19 C.16 D.13
【思路点拨】视图、俯视图是分别从物体正面、上面看,所得到的图形.
【答案】D;
【解析】综合主视图和俯视图,这个几何体的底层最少有3+3+1=7个小正方体,第二层最少有3个,
第三层最少有2个,第四层最少有1个,因此搭成这样的一个几何体至少需要小正方体木块的个数为:7+3+2+1=13个.故答案为:13.
【总结升华】由三视图判断组成原几何体的小正方体的个数与由相同的小正方体构成的几何体画三视图正好相反.
举一反三:
【变式1】如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是________.
【答案】6.
【高清课堂:《空间与图形》专题:投影与视图 例6】
【变式2】下图是由几个相同的小正方体搭成的几何体从三个方向看到的图形,则搭成这个几何体的小正方体的个数是( )个.
A.5 B.6 C.7 D.8
【答案】B.
2.美术课上,老师要求同学们将如图所示的白纸只沿虚线剪开,用裁开的纸片和白纸上的阴影部份围成一个立体模型,然后放在桌面上,下面四个示意图中,只有一个符合上述要求,那么这个示意图是( )
A. B.
C. D.
【思路点拨】动手操作看得到小正方体的阴影部分的具体部位即可.
【答案】B
【解析】动手操作折叠成正方体的形状放置到白纸的阴影部分上,所得正方体中的阴影部分应紧靠白纸, 故选B.
【总结升华】用到的知识与正方体展开图有关,考察学生空间想象能力.建议学生在平时的教学过程中应结合实际模型将展开图的若干种情况分析清楚.
举一反三:
【变式】如图所示的是以一个由一些相同的小正方体组成的简单几何体的主视图和俯视图.设组成这个几何体的小正方体的个数为n,请写出n的所有可能的值.
【答案】n为8,9,10,11.
3.下列图形中经过折叠能围成一个棱柱的是( )
A. B. C. D.
【思路点拨】利用四棱柱及其表面展开图的特点解题.
【答案】D;
【解析】
A、侧面少一个长方形,故不能; B、侧面多一个长方形,折叠后不能围成棱柱,故不能; C、折叠后少一个底面,不能围成棱柱; 只有D能围成四棱柱. 故选D.
【总结升华】四棱柱的侧面展开图为四个长方形组成的大长方形.
举一反三:
【高清课堂:《空间与图形》专题:投影与视图 课堂练习3】
【变式】如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AB、BB1、BC的中点,沿EG、EF、FG将这个正方体切去一个角后,得到的几何体的俯视图是( )
A. B. C. D.
【答案】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.从上面看易得1个正方形,但上面少了一个角,在俯视图中,右下角有一条线段.故选B.
类型二、投影有关问题
4.如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,求塔高AB的长.
【思路点拨】过点D构造矩形,把塔高的影长分解为平地上的BD,斜坡上的DE.然后根据影长的比分别求得AG,GB长,把它们相加即可.
【答案与解析】
【解析1】
解:如图1,过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.可得矩形BDFG.
由题意得:.
∴DF=DE×1.6÷2=14.4(m).
∴GF=BD=CD=6m.
又∵.
∴AG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m.
图1 图2
【解析2】
如图2,作DG∥AE,交AB于点G,BG的影长为BD,AG 的影长为DE,
由题意得:.
∴AG=18×1.6÷2=14.4(m).
又∵.
∴BG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m.
【总结升华】运用所学的解直角三角形的知识解决实际生活中的问题,要求我们要具备数学建模能力(即将实际问题转化为数学问题).
类型三、投影视图综合问题
5.用小立方体搭成一个几何体,使它的主视图和俯视图如图所示,搭建这样的几何体最多要 小立方体.
【思路点拨】从正视图和侧视图考查几何体的形状,从俯视图看出几何体的小立方块最多的数目.
【答案】17.
【解析】
解:由主视图可知,它自下而上共有3列,第一列3块,第二列2块,第三列1块. 由俯视图可知,它自左而右共有3列,第二列各3块,第三列1块,从空中俯视的块数只要最低层有一块即可.因此,综合两图可知这个几何体的形状不能确定;如图,最多时有3×5+2×1=17块小立方体. 故答案为17.
【总结升华】本题考查简单空间图形的三视图,考查空间想象能力,是基础题,但很容易出错.
6.太阳光线与水平线的夹角在新疆地区的变化较大,夏至时夹角最大,冬至时夹角最小,最小夹角约为28度.现有两幢居民住宅楼高为15米,两楼相距20米,如图所示. (1)在冬至时,甲楼的影子在乙楼上有多高? (2)若在本小区内继续兴建同样高的住宅楼,楼距至少应该多少米,才不影响楼房的采光?(前一幢楼房的影子不能落在后一幢楼房上)(计算结果精确到0.1米)
【思路点拨】
(1)如图,构造直角三角形ADE,则∠ADE=28°,DE=BC=20,在这个三角形中已知一边和一个锐角,满足解直角三角形的条件,可求出AE的长从而求得CD的长. (2)在△ABC中,由角C的值和AB的高,满足解直角三角形的条件,可求出BC的长.
【答案与解析】
解:(1)如图所示, 作DE⊥AB,垂足为E, 由题意可知∠ADE=28°,DE=BC=20, 在Rt△ADE中,tan∠ADE= , AE=DE?tan∠DAE=20?tan28°≈10.6, 则DC=EB=AB-AE=15-10.6=4.4. 即冬至时甲楼的影子在乙楼上约4.4米高. (2)若要不影响要房间的采光,如图所示在Rt△ABC中,AB=15,∠C=28°, BC= .
答:楼距至少28.2米,才不影响楼房的采光.
【总结升华】本题是解直角三角形在生活中的实际应用,做到学数学,用数学,才是学习数学的意义.
7.如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过底面圆的圆心,其高 m,底面半径为2m.某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4m. (1)求∠B的度数; (2)若∠ACP=2∠B,求光源A距平面的高度.
【思路点拨】
(1)如下图所示,过点D作DF垂直BC于点F.由题意,得DF= ,EF=2,BE=4,在Rt△DFB中,tan∠B= ,由此可以求出∠B;
(2)过点A作AH垂直BP于点H.因为∠ACP=2∠B=60°所以∠BAC=30°,AC=BC=8.在Rt△ACH中,AH=AC?Sin∠ACP,所以可以求出AH了,即求出了光源A距平面的高度.
【答案与解析】
解:(1)过点D作DF垂直BC于点F. 由题意,得DF=,EF=2,BE=4. 在Rt△DFB中,tan∠B=, 所以∠B=30°; (2)过点A作AH垂直BP于点H. ∵∠ACP=2∠B=60°, ∴∠BAC=30°, ∴AC=BC=8, 在Rt△ACH中,AH=AC?Sin∠ACP=,
即光源A距平面的高度为m.
【总结升华】
本题考查了学生运用三角函数知识解决实际问题的能力,又让学生感受到生活处处有数学,数学在生产生活中有着广泛的作用.
中考总复习:投影与视图—巩固练习
【巩固练习】
一、选择题 1.如图所示的一组几何体的俯视图是( )
2.如图,形状相同、大小相等的两个小木块放在一起,其俯视图如图所示,则其主视图是( )
3.如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为( )
4.如图是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A. B. C. D.
5.如图,是由若干个同样大小的立方体搭成的几何体的俯视图,小正方形中的数字表示该位置立方体的个数,则这个几何体的主视图是( )
6.如图是一个包装纸盒的三视图(单位:cm),则制作一个纸盒所需纸板的面积是( )
A. B. C. D.
二、填空题
7.长方体的主视图与俯视图如图所示,则这个长方体的体积是 .
8.如图,上体育课,甲、乙两名同学分别站在C,D的位置时,乙的影子恰好在甲的影子里边,已知甲、乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是_________米.
第7题 第8题 第9题 第10题
9.如图,小明在A时测得某树影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为________m.
10.如图是由大小相同的小正方体组成的简单几何体的主视图和左视图,那么组成这个几何体的小正方体的个数最多为__________.
11.如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是_________.
12.如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕点A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设垂直于地面时的影长为AC(假定AC>AB),影长的最大值为m,最小值为n,那么下列结论:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小,其中正确结论的序号是___ _____.
三、解答题
13.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,求其影子B1C1的长;当小明继续走剩下路程的到B2处时,求其影子B2C2的长;当小明继续走剩下路程的到B3处,……按此规律继续走下去,当小明走剩下路程的到Bn处时,其影子的长为________m(直接用含n的代数式表示).
14. 如图,某居民小区内A、B两楼之间的距离MN=30m,两楼的高都是20m,A楼在B楼正南,B楼窗户朝南.B楼内一楼住户的窗台离小区地面的距离DN=2m,窗户高CD=1.8m.当正午时刻太阳光线与地面成30°角时,A楼的影子是否影响B楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.(参考数据:=1.414,=1.732,=2.236)
15.某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°角.(≈1.4,≈1.7)
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.(用图(2)解答)
①求树与地面成45°角时的影长;
②求树的最大影长.
16..如图(1)是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形,现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图(2)),然后用这条平行四边形纸带按如图(3)的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图(2)中,计算裁剪的角度∠BAD;
(2)计算按图(3)方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
【答案与解析】
一、选择题 1.【答案】B;
【解析】圆锥的俯视图是带圆心的圆,六棱柱的俯视图是正六边形,所以它们的俯视图是B.
2.【答案】D;
【解析】只有D答案体现了后排只有一层.
3.【答案】A;
【解析】根据中心投影的性质,小亮的影长y随x逐渐变小再逐渐变大,且y是x的一次函数.
4.【答案】B;
【解析】该几何体是底面圆直径为a,母线长为c的圆锥,其侧面积.
5.【答案】D;
【解析】根据俯视图可知主视图有两列,左边一列的最大高度为2,右边一列的高度是3,故选D.
6.【答案】C;
【解析】由三视图知此包装纸盒是一个正六棱柱,其全面积
.
二、填空题
7.【答案】24;
【解析】由主视图和俯视图知长方体的长宽高分别为4,2,3,所以V=4×2×3=24.
8.【答案】6;
【解析】设甲的影长AC=x米,则乙的影长AD=(x-1)米.根据同一时刻物高与影长成比例,
可得.解得x=6(米).
9.【答案】4;
【解析】如图,设树高CD=h,在Rt△CEF中,由题意得ED=2,FD=8.由Rt△CDE∽△RFCD,
可得.即.∴ CD2=16.故CD=4m.即树的高度为4m.
10.【答案】7:
【解析】由主视图知几何体左右共两排,由左视图知几何体前后三排,且左排最高两层,所以组成这个几何体的小正方体的个数最多为7个.
11.【答案】6;
【解析】主视图能反映每一列的最大高度,左视图能反映每一行的最大高度,俯视图能反映行列数,由三视图可发现俯视图中行列的高度如图所示,则图中棱长为1的正方体的个数
是1+1+1+1+2=6(个).
12.【答案】①③④ ;
【解析】如图所示.当AB转至AE时影长最大值m=AD>AC,当AB转至AB′时影长最小值;
当AB转至AB′时影长最小值n=AB,影子的长度先增大后减小,所以正确结论的
序号是①③④.
三、解答题
13.【答案与解析】
解:(1)如图:
(2)由题意得△ABC∽△GHC.
∴.
∴.
∴GH=4.8m.
(3)∵△A1B1C1∽△GHC1,
∴.设B1C1长为xm,
则.解得,即B1C1=.
同理,解得,.
14.【答案与解析】
解:如图,设光线FE影响到B楼的E处,作EG⊥FM于点G,由题知,EG=MN=30m,∠FEG=30°.
则FG=30°×tan30°=30×==17.32 (m),
MG=FM-GF=20-17.32=2.68-2=0.68(m).因为DN=2m,CD=1.8m,
所以ED=2.68-2=0.68(m),即A楼影子影响到B楼一楼采光,挡住该户窗户0.68m.
15.【答案与解析】
解:(1)AB=ACtan30°=12×≈7(米).(结果也可以保留一位小数,下同)
答:树高约7米.
(2) 解析:①在Rt△ABC中,AB=ACtan30°;②过B1作B1N⊥AC1,在Rt△AB1N和Rt△B1NC1中分别求AN和NC1.当树与地面成60°角时影长最大(如图AC2)
①如图,B1N=AN=ABsin 45°=≈5(米).NC1=NB1tan60°=≈8(米).
AC1=AN+NC1=5+8≈13(米).
答:树与地面成45°角时影长为13米.
②如图,当树与地面成60°角时影长最大,为AC2=2AB2≈14(米)(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
16.【答案与解析】
解析:(1)观察图(3)的包贴方式知AB的长等于三棱柱的底面周长,
则AB=30.由AM=15可以求出∠ABM=30°.
由AD∥BC求出∠BAD=∠ABM=30°.
(2)可将三棱柱的侧面展开,利用平面图形计算MC的长.
解:(1)由图(3)的包贴方法知:AB的长等于三棱柱的底面周长,
∴AB=30.
∵纸带宽为15,sin∠DAB=sin∠ABM=,
∴∠DAB=30°.
(2)在图(3)中,将三棱柱沿过点A的侧棱剪开,得到如图甲的侧面展开图,
将图甲中的△ABE向左平移30 cm,△CDF向右平移30 cm,拼成如图乙中的平行四边形ABCD,
此平行四边形即为图(2)中的平行四边形ABCD.
由题意,知:BC=BE+CE=2CE=2×,
∴所需矩形纸带的长为MB+BC=30·cos30°+(cm).
同课章节目录
