22.1.4《二次函数系数与图象的关系》复习课件
文档属性
| 名称 | 22.1.4《二次函数系数与图象的关系》复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-27 17:01:02 | ||
图片预览









文档简介
(共31张PPT)
22.1.4二次函数y=ax2+bx+c
图象和性质(2)
数学人教版版 九年级上
复习:函数y=ax?+bx+c的对称轴、顶点坐标是什么?
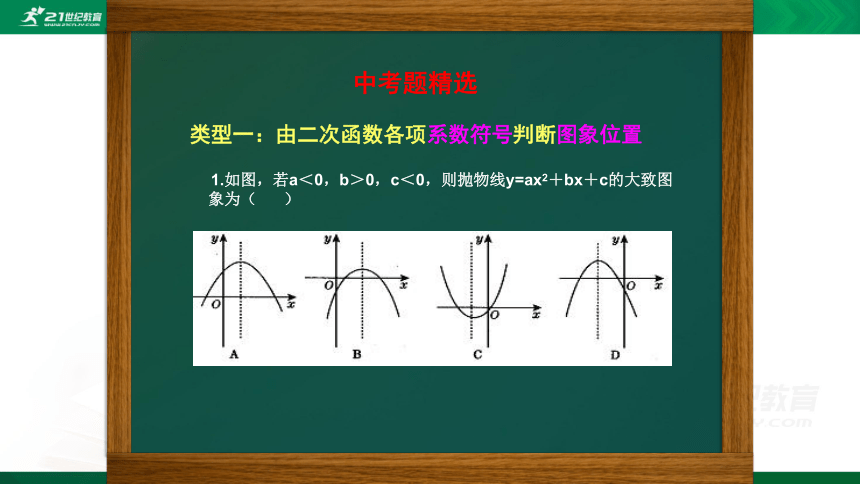
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
(1)a 决定抛物线的开口方向和大小
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
(1)a 决定抛物线的开口方向和大小
(2)b 联合a决定对称轴 的位置
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
(1)a 决定抛物线的开口方向和大小
(2)b 联合a决定对称轴 的位置
(3)c 决定抛物线与y轴的交点位置
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
(1)a 决定抛物线的开口方向和大小
(2)b 联合a决定对称轴 的位置
(3)c 决定抛物线与y轴的交点位置
(4)b2-4ac 决定抛物线与x轴交点的个数
⑴a决定抛物线的开口方向:
a>0 开口向上
a<0 开口向下
⑵ a,b决定抛物线对称轴的位置:
(对称轴是直线x = -— )
①?a,b同号<=> 对称轴在y轴左侧;
②? b=0 <=> 对称轴是y轴;
③ a,b异号<=> 对称轴在y轴右侧
2a
b
【左同右异】
⑶ c决定抛物线与y轴交点的位置:
①??c>0 ,图象与y轴交点在x轴上方;
②??c=0 ,图象过原点;
③??c<0 ,图象与y轴交点在x轴下方。
⑷顶点坐标是( , )。
中考题精选
类型一:由二次函数各项系数符号判断图象位置
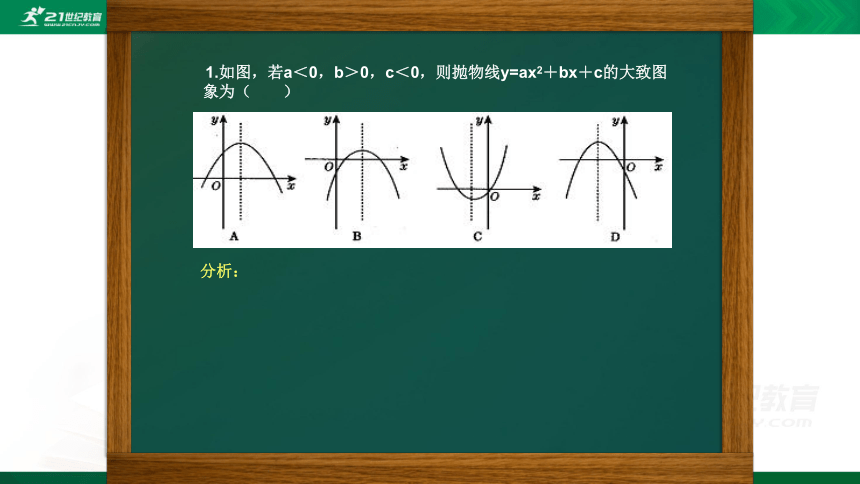
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:此题可用排除法解决
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:此题可用排除法解决
a<0 说明抛物线开口向下,排除选项C
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:此题可用排除法解决
a<0 说明抛物线开口向下,排除选项C
b>0 说明a和b为异号,根据对称轴“左同右异”,
可知对称轴位于y轴右侧,排除选项D
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:此题可用排除法解决
a<0 说明抛物线开口向下,排除选项C
b>0 说明a和b为异号,根据对称轴“左同右异”,
可知对称轴位于y轴右侧,排除选项D
c<0 说明抛物线交与y轴的负半轴,排除选项A,
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( B )
分析:此题可用排除法解决
a<0 说明抛物线开口向下,排除选项C
b>0 说明a和b为异号,根据对称轴“左同右异”,
可知对称轴位于y轴右侧,排除选项D
c<0 说明抛物线交与y轴的负半轴,排除选项A,
中考题精选
类型二:由二次函数图象位置判断式子符号
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=-3时,y <0
正确结论有(填序号):
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
⑤由③和④可得y=4a-2b+c=4a-2(-2a)+c=8a+c > 0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
⑤由③和④可得y=4a-2b+c=4a-2(-2a)+c=8a+c > 0
⑥点(-1,0)关于对称轴 x=1的对称点为(3,0),当x=3时,y <0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号): ③ ④ ⑥
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
⑤由③和④可得y=4a-2b+c=4a-2(-2a)+c=8a+c > 0
⑥点(-1,0)关于对称轴 x=1的对称点为(3,0),当x=3时,y <0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号): ③ ④ ⑥
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
⑤由③和④可得y=4a-2b+c=4a-2(-2a)+c=8a+c > 0
⑥点(-1,0)关于对称轴 x=1的对称点为(3,0),当x=3时,y <0
构造法与特值法
4.若一次函数 y=ax+b 的图象经过第二、三、四象限,则二次函数 y=ax2+bx-3 的大致图象是 ( )
5.在同一直角坐标系中,二次函数 y=ax2+bx+c 与一次函数y=ax+c的大致图象可能是 ( )
C
C
课堂小结
1.同学们有什么收获?提出来共同分享。
2.同学们还有什么困惑?提出来大家交流。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.1.4二次函数y=ax2+bx+c
图象和性质(2)
数学人教版版 九年级上
复习:函数y=ax?+bx+c的对称轴、顶点坐标是什么?
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
(1)a 决定抛物线的开口方向和大小
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
(1)a 决定抛物线的开口方向和大小
(2)b 联合a决定对称轴 的位置
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
(1)a 决定抛物线的开口方向和大小
(2)b 联合a决定对称轴 的位置
(3)c 决定抛物线与y轴的交点位置
二次函数的图象与各项系数之间的关系
.
二次函数y=ax2+bx+c(a≠0)
(1)a 决定抛物线的开口方向和大小
(2)b 联合a决定对称轴 的位置
(3)c 决定抛物线与y轴的交点位置
(4)b2-4ac 决定抛物线与x轴交点的个数
⑴a决定抛物线的开口方向:
a>0 开口向上
a<0 开口向下
⑵ a,b决定抛物线对称轴的位置:
(对称轴是直线x = -— )
①?a,b同号<=> 对称轴在y轴左侧;
②? b=0 <=> 对称轴是y轴;
③ a,b异号<=> 对称轴在y轴右侧
2a
b
【左同右异】
⑶ c决定抛物线与y轴交点的位置:
①??c>0 ,图象与y轴交点在x轴上方;
②??c=0 ,图象过原点;
③??c<0 ,图象与y轴交点在x轴下方。
⑷顶点坐标是( , )。
中考题精选
类型一:由二次函数各项系数符号判断图象位置
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:此题可用排除法解决
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:此题可用排除法解决
a<0 说明抛物线开口向下,排除选项C
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:此题可用排除法解决
a<0 说明抛物线开口向下,排除选项C
b>0 说明a和b为异号,根据对称轴“左同右异”,
可知对称轴位于y轴右侧,排除选项D
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
分析:此题可用排除法解决
a<0 说明抛物线开口向下,排除选项C
b>0 说明a和b为异号,根据对称轴“左同右异”,
可知对称轴位于y轴右侧,排除选项D
c<0 说明抛物线交与y轴的负半轴,排除选项A,
1.如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( B )
分析:此题可用排除法解决
a<0 说明抛物线开口向下,排除选项C
b>0 说明a和b为异号,根据对称轴“左同右异”,
可知对称轴位于y轴右侧,排除选项D
c<0 说明抛物线交与y轴的负半轴,排除选项A,
中考题精选
类型二:由二次函数图象位置判断式子符号
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=-3时,y <0
正确结论有(填序号):
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
⑤由③和④可得y=4a-2b+c=4a-2(-2a)+c=8a+c > 0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号):
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
⑤由③和④可得y=4a-2b+c=4a-2(-2a)+c=8a+c > 0
⑥点(-1,0)关于对称轴 x=1的对称点为(3,0),当x=3时,y <0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号): ③ ④ ⑥
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
⑤由③和④可得y=4a-2b+c=4a-2(-2a)+c=8a+c > 0
⑥点(-1,0)关于对称轴 x=1的对称点为(3,0),当x=3时,y <0
3、二次函数y=ax2+bx+c的图象如图所示,则下列说法:
abc <0
②4ac-b2>0
③2a+b=0
④4a+c>2b
⑤8a+c<0
⑥当x=3时,y <0
正确结论有(填序号): ③ ④ ⑥
分析:
①开口向上:a>0 ;左同右异:b <0 ;交y轴负半轴:c <0
②与x轴有两个交点:b2-4ac>0
③对称轴 =1可得2a=-b
④把x=-2代入解析式得:y=4a-2b+c;又x=-2时,y >0 ;
⑤由③和④可得y=4a-2b+c=4a-2(-2a)+c=8a+c > 0
⑥点(-1,0)关于对称轴 x=1的对称点为(3,0),当x=3时,y <0
构造法与特值法
4.若一次函数 y=ax+b 的图象经过第二、三、四象限,则二次函数 y=ax2+bx-3 的大致图象是 ( )
5.在同一直角坐标系中,二次函数 y=ax2+bx+c 与一次函数y=ax+c的大致图象可能是 ( )
C
C
课堂小结
1.同学们有什么收获?提出来共同分享。
2.同学们还有什么困惑?提出来大家交流。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
