人教版数学五年级下册3.3.3《容积和容积单位》教案(表格版)
文档属性
| 名称 | 人教版数学五年级下册3.3.3《容积和容积单位》教案(表格版) |
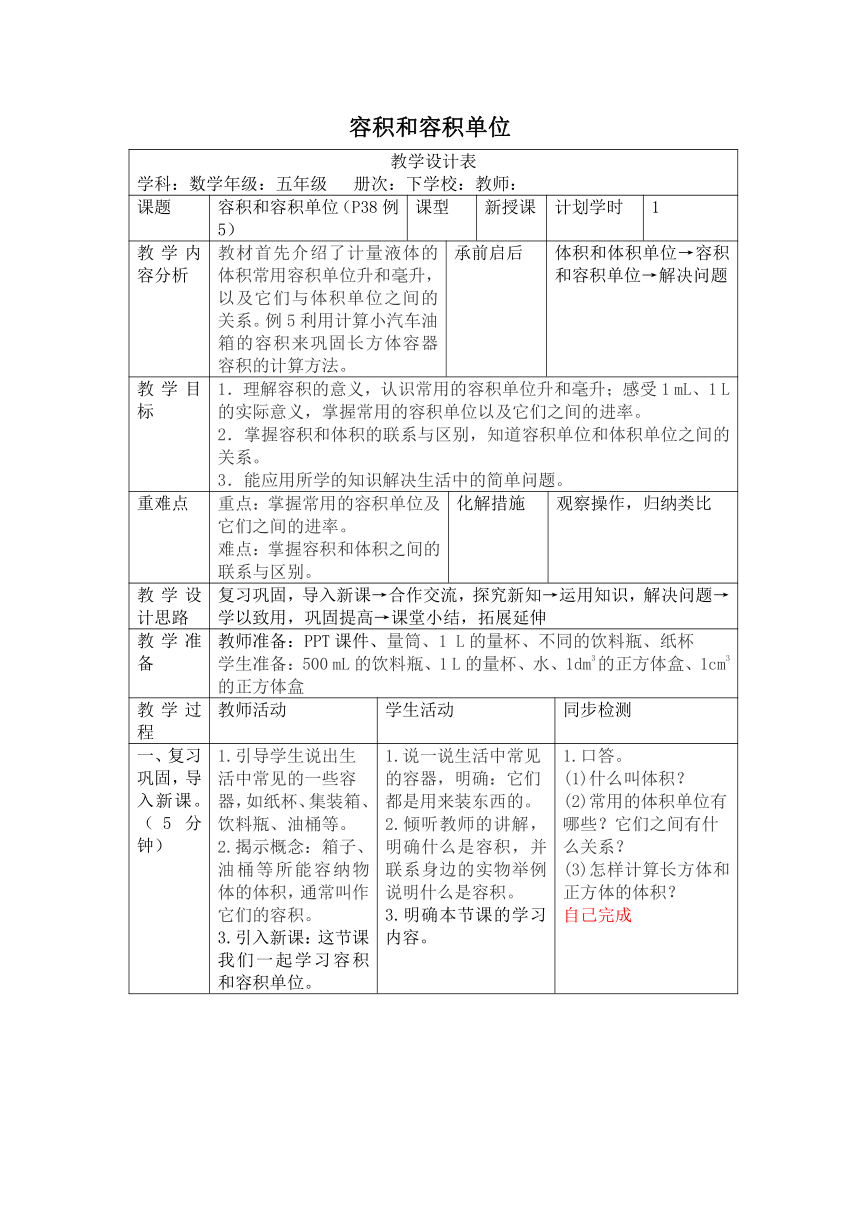
|
|
| 格式 | zip | ||
| 文件大小 | 30.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-28 00:00:00 | ||
图片预览


文档简介
容积和容积单位
教学设计表
学科:数学年级:五年级 册次:下学校:教师:
课题
容积和容积单位(P38例5)
课型
新授课
计划学时
1
教学内容分析
教材首先介绍了计量液体的体积常用容积单位升和毫升,以及它们与体积单位之间的关系。例5利用计算小汽车油箱的容积来巩固长方体容器容积的计算方法。
承前启后
体积和体积单位→容积和容积单位→解决问题
教学目标
1.理解容积的意义,认识常用的容积单位升和毫升;感受1 mL、1 L的实际意义,掌握常用的容积单位以及它们之间的进率。
2.掌握容积和体积的联系与区别,知道容积单位和体积单位之间的关系。
3.能应用所学的知识解决生活中的简单问题。
重难点
重点:掌握常用的容积单位及它们之间的进率。
难点:掌握容积和体积之间的联系与区别。
化解措施
观察操作,归纳类比
教学设计思路
复习巩固,导入新课→合作交流,探究新知→运用知识,解决问题→学以致用,巩固提高→课堂小结,拓展延伸
教学准备
教师准备:PPT课件、量筒、1 L的量杯、不同的饮料瓶、纸杯
学生准备:500 mL的饮料瓶、1 L的量杯、水、1dm3的正方体盒、1cm3的正方体盒
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.引导学生说出生活中常见的一些容器,如纸杯、集装箱、饮料瓶、油桶等。
2.揭示概念:箱子、油桶等所能容纳物体的体积,通常叫作它们的容积。
3.引入新课:这节课我们一起学习容积和容积单位。
1.说一说生活中常见的容器,明确:它们都是用来装东西的。
2.倾听教师的讲解,明确什么是容积,并联系身边的实物举例说明什么是容积。
3.明确本节课的学习内容。
1.口答。
(1)什么叫体积?
(2)常用的体积单位有哪些?它们之间有什么关系?
(3)怎样计算长方体和正方体的体积?
自己完成
二、合作交流,探究新知。(20分钟)
1.引导学生自学教材第38页的内容,用笔画出这一部分的重点知识或标出有疑问的地方,然后集体交流。
2.认识1 L、1 mL。
(1)出示容积是1 L的量杯,引导学生猜想它能装多少水。
(2)组织学生拿出准备好的学具(500 mL的饮料瓶、1 L的量杯),动手操作,验证猜想。
3.探究容积单位和体积单位间的关系。
(1)引导学生动手操作,自主得出结论。
师:将1 L水倒入1 dm3的正方体盒中;将1 mL水注入1 cm3的正方体盒中,你发现了什么?通过你的发现,你得出了什么结论?
(2)小结:计量容积时一般就用体积单位,计量液体的体积时,常用升或毫升做单位。
4.引导学生讨论体积和容积的联系和区别。
1.自学教材第38页的内容,交流、汇报自己的学习收获:计量容积一般就用体积单位,计量液体的体积,如水、油等,常用容积单位升和毫升,升和毫升用字母表示分别是L和mL。
2.(1)观察教师手中的量杯,大胆猜想。
(2)动手操作,验证自己的猜想,通过实验得出1 L的量杯能装2瓶500 mL的水,得出1 L=1000 mL。
3.(1)在小组内操作:将1 L水倒入1 dm3的正方体盒中;再将1 mL水注入1 cm3的正方体盒中。小组内交流自己的发现,明确:1 L=1 dm3,1 mL=1 cm3。
(2)倾听教师的小结,明确容积单位的应用及容积的计算方法,强化认识。
4.明确:容器容积的计算方法和体积的计算方法相同,但要从容器的里面量长、宽、高。
/
3.单位换算。
5 L=(5000)mL
600 mL=(0.6)L
7.5 L=(7.5)dm3=
(7500)cm3
785 mL=(785)cm3=(0.785)dm3
4 L=(4000)mL
4800 mL=(4.8)L
2.4 L=(2400)mL
500 mL=(0.5)L
三、运用知识,解决问题。(6分钟)
1.课件出示例5,引导学生讨论:求可以装多少升汽油,就是求什么?需要什么条件?用什么公式计算?
2.指导学生独立列式解答,并汇报。
1.认真分析题意,回答问题:求可以装多少升汽油就是求油箱的容积,要先知道从里面测量的长、宽、高各是多少,再用长方体的体积计算公式进行计算。
2.尝试列式并计算,注意书写格式。
/
四、学以致用,巩固提高。(5分钟)
1.完成教材第40页第2题。
2.完成教材第40页第5题。
1.独立完成后,全班交流,交流时说出单位间的进率。
2. 分析题意,独立列式解答,并交流、汇报。
5.一辆卡车的车厢是长方体,从里面量长3 m,宽2 m,高0.5 m,求这辆卡车车厢的容积。
3×2×0.5=3(m3)
五、课堂小结,拓展延伸。(4分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.容积和体积的联系:(1)容积的大小可以通过容器所能容纳的物体的体积显示出来;(2)容积的计算方法与体积的计算方法相同。
3.容积和体积的区别:(1)意义不同;(2)计算时,测量数据的方法不同;(3)有容积的物体一定有体积,但有体积的物体不一定有容积。
教师个人补充意见:
板书设计
容积和容积单位
容器所能容纳物体的体积,通常叫作它的容积。
1 L=1 dm3
1 mL=1 cm3
1 L=1000 mL
?
培优作业
有甲、乙两个水箱,从里面量甲水箱长12 dm,宽8 dm,高5 dm;乙水箱长8 dm,宽8 dm,高6 dm。甲水箱装满水,乙水箱空着。现将甲水箱里的一部分水抽到乙水箱中,使两个水箱的水面高度一样。现在两个水箱的水面高度是多少分米?
12×8×5÷(12×8+8×8)
=480÷(96+64)
=480÷160
=3(dm)
提示:两个水箱水面高度一样,就相当于把这两个水箱转化成一个大的水箱,这个大水箱的底面积就等于甲、乙两个水箱的底面积之和。求现在的水面高度,也就是求转化后的大水箱中水面的高度。
教学反思
联系生活实际展开教学,能让学生感受到学习数学的必要性,也能提高学生学习数学的兴趣。以问题的形式,将生活中的知识与数学学习有机结合,这样不但能加深学生对容积概念的理解,还能使学生进一步理解物体的体积和容积的区别与联系。
微课设计点
教师可围绕“容积单位和体积单位的关系”设计微课。
教学设计表
学科:数学年级:五年级 册次:下学校:教师:
课题
容积和容积单位(P38例5)
课型
新授课
计划学时
1
教学内容分析
教材首先介绍了计量液体的体积常用容积单位升和毫升,以及它们与体积单位之间的关系。例5利用计算小汽车油箱的容积来巩固长方体容器容积的计算方法。
承前启后
体积和体积单位→容积和容积单位→解决问题
教学目标
1.理解容积的意义,认识常用的容积单位升和毫升;感受1 mL、1 L的实际意义,掌握常用的容积单位以及它们之间的进率。
2.掌握容积和体积的联系与区别,知道容积单位和体积单位之间的关系。
3.能应用所学的知识解决生活中的简单问题。
重难点
重点:掌握常用的容积单位及它们之间的进率。
难点:掌握容积和体积之间的联系与区别。
化解措施
观察操作,归纳类比
教学设计思路
复习巩固,导入新课→合作交流,探究新知→运用知识,解决问题→学以致用,巩固提高→课堂小结,拓展延伸
教学准备
教师准备:PPT课件、量筒、1 L的量杯、不同的饮料瓶、纸杯
学生准备:500 mL的饮料瓶、1 L的量杯、水、1dm3的正方体盒、1cm3的正方体盒
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.引导学生说出生活中常见的一些容器,如纸杯、集装箱、饮料瓶、油桶等。
2.揭示概念:箱子、油桶等所能容纳物体的体积,通常叫作它们的容积。
3.引入新课:这节课我们一起学习容积和容积单位。
1.说一说生活中常见的容器,明确:它们都是用来装东西的。
2.倾听教师的讲解,明确什么是容积,并联系身边的实物举例说明什么是容积。
3.明确本节课的学习内容。
1.口答。
(1)什么叫体积?
(2)常用的体积单位有哪些?它们之间有什么关系?
(3)怎样计算长方体和正方体的体积?
自己完成
二、合作交流,探究新知。(20分钟)
1.引导学生自学教材第38页的内容,用笔画出这一部分的重点知识或标出有疑问的地方,然后集体交流。
2.认识1 L、1 mL。
(1)出示容积是1 L的量杯,引导学生猜想它能装多少水。
(2)组织学生拿出准备好的学具(500 mL的饮料瓶、1 L的量杯),动手操作,验证猜想。
3.探究容积单位和体积单位间的关系。
(1)引导学生动手操作,自主得出结论。
师:将1 L水倒入1 dm3的正方体盒中;将1 mL水注入1 cm3的正方体盒中,你发现了什么?通过你的发现,你得出了什么结论?
(2)小结:计量容积时一般就用体积单位,计量液体的体积时,常用升或毫升做单位。
4.引导学生讨论体积和容积的联系和区别。
1.自学教材第38页的内容,交流、汇报自己的学习收获:计量容积一般就用体积单位,计量液体的体积,如水、油等,常用容积单位升和毫升,升和毫升用字母表示分别是L和mL。
2.(1)观察教师手中的量杯,大胆猜想。
(2)动手操作,验证自己的猜想,通过实验得出1 L的量杯能装2瓶500 mL的水,得出1 L=1000 mL。
3.(1)在小组内操作:将1 L水倒入1 dm3的正方体盒中;再将1 mL水注入1 cm3的正方体盒中。小组内交流自己的发现,明确:1 L=1 dm3,1 mL=1 cm3。
(2)倾听教师的小结,明确容积单位的应用及容积的计算方法,强化认识。
4.明确:容器容积的计算方法和体积的计算方法相同,但要从容器的里面量长、宽、高。
/
3.单位换算。
5 L=(5000)mL
600 mL=(0.6)L
7.5 L=(7.5)dm3=
(7500)cm3
785 mL=(785)cm3=(0.785)dm3
4 L=(4000)mL
4800 mL=(4.8)L
2.4 L=(2400)mL
500 mL=(0.5)L
三、运用知识,解决问题。(6分钟)
1.课件出示例5,引导学生讨论:求可以装多少升汽油,就是求什么?需要什么条件?用什么公式计算?
2.指导学生独立列式解答,并汇报。
1.认真分析题意,回答问题:求可以装多少升汽油就是求油箱的容积,要先知道从里面测量的长、宽、高各是多少,再用长方体的体积计算公式进行计算。
2.尝试列式并计算,注意书写格式。
/
四、学以致用,巩固提高。(5分钟)
1.完成教材第40页第2题。
2.完成教材第40页第5题。
1.独立完成后,全班交流,交流时说出单位间的进率。
2. 分析题意,独立列式解答,并交流、汇报。
5.一辆卡车的车厢是长方体,从里面量长3 m,宽2 m,高0.5 m,求这辆卡车车厢的容积。
3×2×0.5=3(m3)
五、课堂小结,拓展延伸。(4分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.容积和体积的联系:(1)容积的大小可以通过容器所能容纳的物体的体积显示出来;(2)容积的计算方法与体积的计算方法相同。
3.容积和体积的区别:(1)意义不同;(2)计算时,测量数据的方法不同;(3)有容积的物体一定有体积,但有体积的物体不一定有容积。
教师个人补充意见:
板书设计
容积和容积单位
容器所能容纳物体的体积,通常叫作它的容积。
1 L=1 dm3
1 mL=1 cm3
1 L=1000 mL
?
培优作业
有甲、乙两个水箱,从里面量甲水箱长12 dm,宽8 dm,高5 dm;乙水箱长8 dm,宽8 dm,高6 dm。甲水箱装满水,乙水箱空着。现将甲水箱里的一部分水抽到乙水箱中,使两个水箱的水面高度一样。现在两个水箱的水面高度是多少分米?
12×8×5÷(12×8+8×8)
=480÷(96+64)
=480÷160
=3(dm)
提示:两个水箱水面高度一样,就相当于把这两个水箱转化成一个大的水箱,这个大水箱的底面积就等于甲、乙两个水箱的底面积之和。求现在的水面高度,也就是求转化后的大水箱中水面的高度。
教学反思
联系生活实际展开教学,能让学生感受到学习数学的必要性,也能提高学生学习数学的兴趣。以问题的形式,将生活中的知识与数学学习有机结合,这样不但能加深学生对容积概念的理解,还能使学生进一步理解物体的体积和容积的区别与联系。
微课设计点
教师可围绕“容积单位和体积单位的关系”设计微课。
