人教版高中数学必修四知识讲解,巩固练习(教学资料,补习资料):第03章 章末检测
文档属性
| 名称 | 人教版高中数学必修四知识讲解,巩固练习(教学资料,补习资料):第03章 章末检测 |  | |
| 格式 | zip | ||
| 文件大小 | 216.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 16:50:59 | ||
图片预览

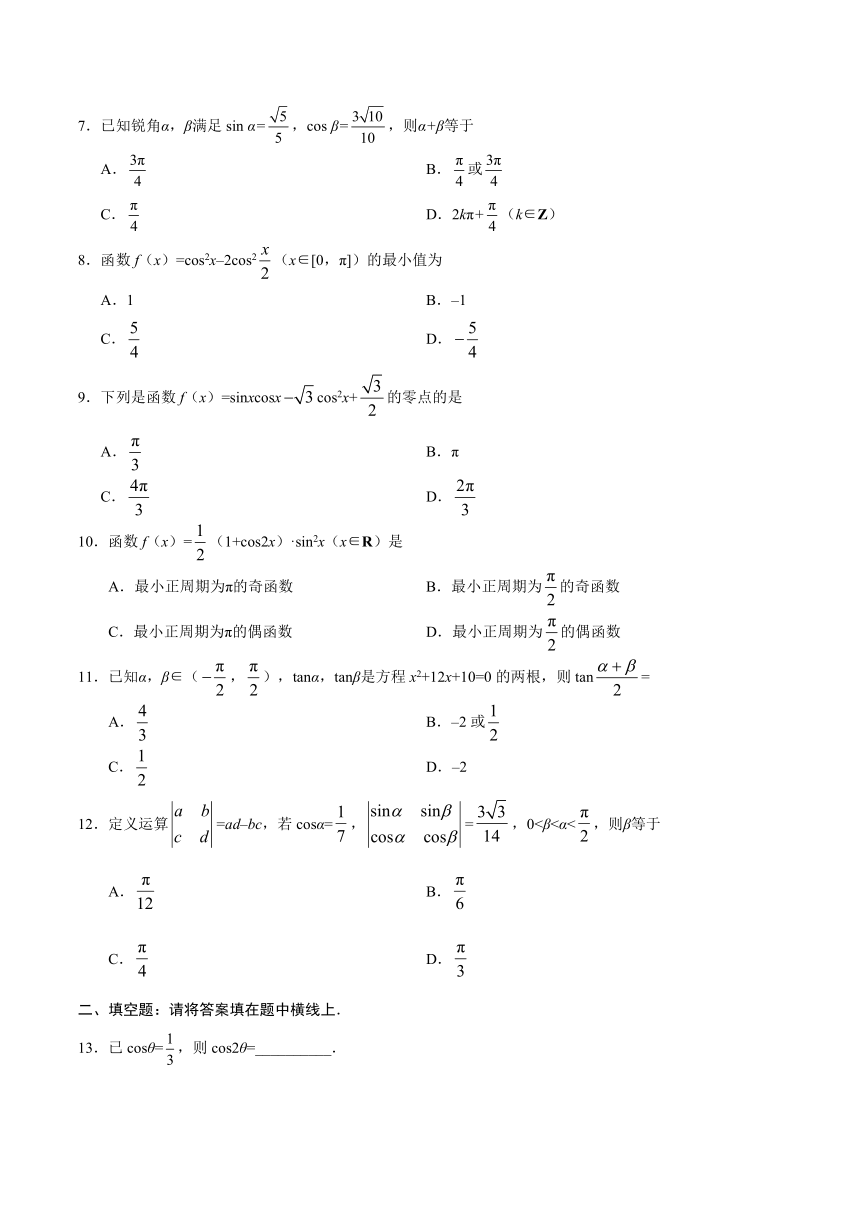

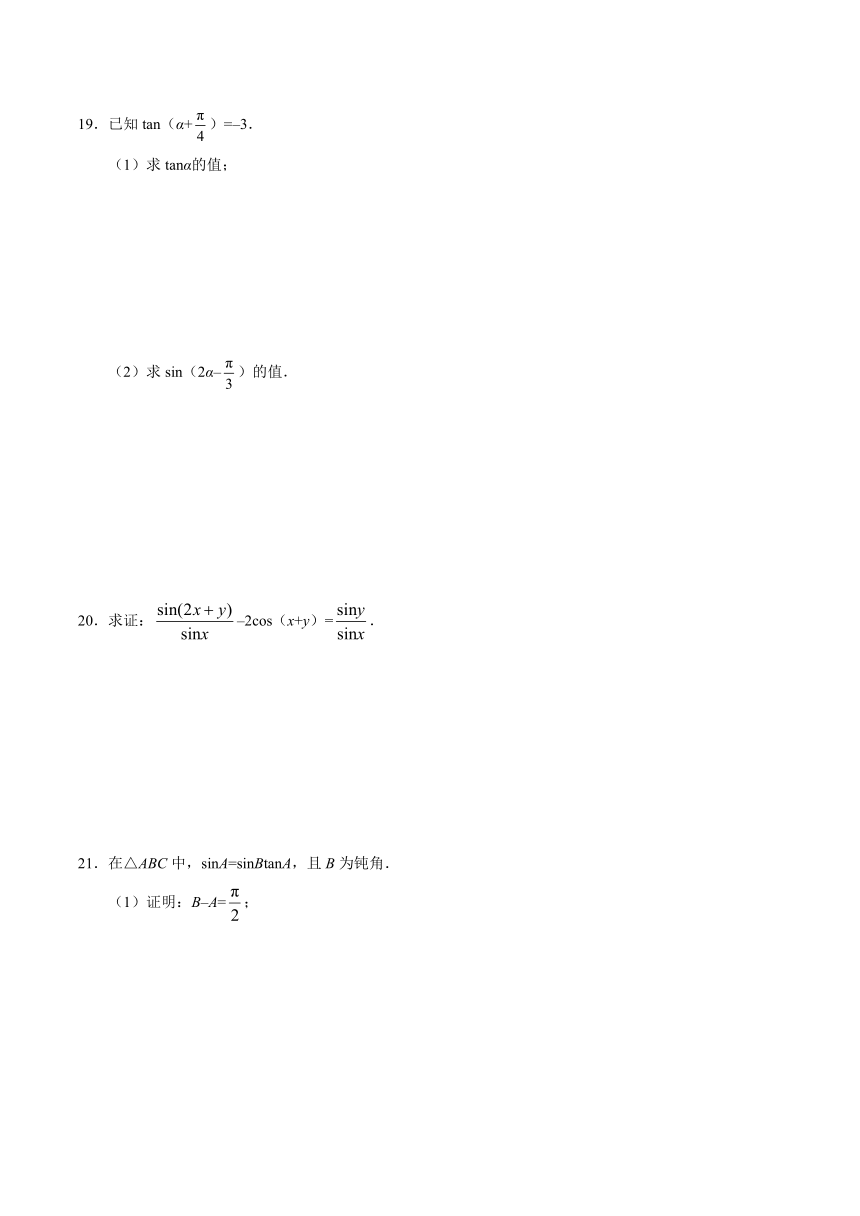

文档简介
第三章 三角恒等变换
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.cos15°的值是
A. B.
C. D.
2.已知,则=
A.7 B.–7
C. D.
3.cos(35°+x)cos(55°–x)–sin(35°+x)sin(55°–x)的值是
A.0 B.–1
C.±1 D.1
4.设α∈(0,2π),已知sin α>cos α,则α的取值范围是
A.() B.(,π)
C.() D.()
5.已知=
A. B.–3
C. D.3
6.已知点A(cos80°,sin80°),B(cos20°,sin20°),则||等于
A. B.
C. D.1
7.已知锐角α,β满足sin α=,cos β=,则α+β等于
A. B.或
C. D.2kπ+(k∈Z)
8.函数f(x)=cos2x–2cos2(x∈[0,π])的最小值为
A.1 B.–1
C. D.
9.下列是函数f(x)=sinxcosxcos2x+的零点的是
A. B.π
C. D.
10.函数f(x)=(1+cos2x)·sin2x(x∈R)是
A.最小正周期为π的奇函数 B.最小正周期为的奇函数
C.最小正周期为π的偶函数 D.最小正周期为的偶函数
11.已知α,β∈(,),tanα,tanβ是方程x2+12x+10=0的两根,则tan=
A. B.–2或
C. D.–2
12.定义运算/=ad–bc,若cosα=/,/=/,0<β<αA./ B./
C./ D./
二、填空题:请将答案填在题中横线上.
13.已cosθ=,则cos2θ=__________.
14.–2cos10°=___________.
15.已知,则=__________.
16.已知,,则tan(α+β)=__________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(1)化简.
(2)已知α∈(0,π),且cos(α–)=.求cosα.
18.已知sinα=,且α为第二象限角.
(1)求sin2α的值;
(2)求tan(α+)的值.
19.已知tan(α+)=–3.
(1)求tanα的值;
(2)求sin(2α–)的值.
20.求证:–2cos(x+y)=.
21.在△ABC中,sinA=sinBtanA,且B为钝角.
(1)证明:B–A=;
(2)求sinA+sinC的取值范围.
22.已知函数f(x)=–cos2xcos+sin2xsin.
(1)求函数f(x)的最小正周期;
(2)若<α<β<,f(α)=,且f(β)=,求角2β–2α的大小.
参考答案
1
2
3
4
5
6
7
8
9
10
11
12
D
D
A
C
B
D
C
D
D
D
D
D
1.【答案】D
【解析】cos15°=cos(45°–30°)=cos45°cos30°+sin45°sin30°=×+×=,故选D.
2.【答案】D
【解析】由得,,所以=,故选D.
3.【答案】A
【解析】cos(35°+x)cos(55°–x)–sin(35°+x)sin(55°–x)=cos[(35°+x)+(55°–x)]=cos90°=0,故选A.
4.【答案】C
【解析】(1)解法一:因为sin α–cos α>0,即sin α–cos α>0,所以sin(α–)>0,所以2kπ<α–<2kπ+π,k∈Z,所以2kπ+<α<2kπ+,k∈Z,又α∈(0,2π),所以α∈().故选C.
解法二:取α=π,因为sin π=0,cos π=–,则sin π>cos π,符合题意,排除A,B;取α=,因为sin=–,=–,则sin=,不符合题意,排除D.故选C.
5.【答案】B
【解析】由cos(+α)=2cos(π–α),可得–sinα=–2cosα,所以tanα=2,
则tan=–3.故选B.
6.【答案】D
【解析】||==
===1.
7.【答案】C
【解析】由sin α=,cos β=,且α,β为锐角,知cos α=,sin β=,故cos(α+β)=cos αcos β–sin αsin β=×– ×=,又0<α+β<π,故α+β=.
8.【答案】D
【解析】由题意,得f(x)=cos2x–2cos2=cos2x–(1+cosx)=cos2x–cosx–1,设t=cosx(x∈[0,π]),y=f(x),则t∈[–1,1],y=t2–t–1=(t)2,所以当t=,即x=时,y取得最小值,为,所以函数f(x)的最小值为,故选D.
9.【答案】D
【解析】f(x)=sinxcosxcos2x+=sin2x(1+cos2x)+=sin(2x),令sin(2x)=0,得2x=kπ,k∈Z,所以x=+,k∈Z,当k=1时,x=.故选D.
10.【答案】D
【解析】由题意,得f(x)=(1+cos2x)(1–cos2x)=(1–cos22x)=sin22x=(1–cos4x).又f(–x)=f(x),所以函数f(x)是最小正周期为的偶函数,选D.
11.【答案】D
【解析】∵α,β∈(,),tanα,tanβ是方程x2+12x+10=0的两根,∴tanα+tanβ=–12,tanα·tanβ=10,∴tanα<0,tanβ<0,∴<α<0,<β<0,∴<<0.又tan(α+β)====,整理得2tan2+3tan2=0,解得tan=–2或tan=(舍去),故选D.
12.【答案】D
【解析】依题意有/=sinαcosβ–cosαsinβ=sin(α–β)=/.∵0<β<α13.【答案】–
【解析】由二倍角的余弦公式可得cos2θ=2cos2θ–1=2×–1=–,故答案为:–.
14.【答案】
【解析】–2cos10°=
=
=.故答案为:.
15.【答案】–
【解析】∵,∴,解得tan,因此,=tanα–=–.故答案为:–.
16.【答案】–
【解析】,∴cosαcos–sinαsincosα,∴–sinα=cosα,∴tanα==–.又,∴tan(α+β)==–.故答案为:–.
17.【解析】(1)=
===.
(2)∵α∈(0,π),∴,
又,
∴,
∴
.
18.【解析】(1)∵sinα=,且α为第二象限角,∴cos,
∴sin2α=2sinαcosα=;
(2)由(1)知tan,∴tan(α+)=.
19.【解析】(1)∵tan(α+)=–3,
∴tanα=tan(α+–)=,
(2)∵sin2α=,
cos2α==–,
∴sin(2α–)=sin2α?cos–cos2α?sin=+.
20.【解析】左边=–2cos(x+y)
=–2cos(x+y)
=
=
==右边.
∴原等式成立.
21.【解析】(1)由sinA=sinBtanA,得=,
所以sinB=cosA,即sinB=sin(+A).
又B为钝角,因此+A∈(,π),故B=+A,即B–A=.
(2)由(1),知C=π–(A+B)=–2A>0,所以A∈(0,).
于是sinA+sinC=sinA+sin(–2A)=sinA+cos2A=–2sin2A+sinA+1=–2(sinA–)2+.
因为0因此<–2(sinA–)2+≤,
即sinA+sinC的取值范围是(,].
22.【解析】(1)因为f(x)=–cos2xcos+sin2xsin,
所以f(x)=cos2xcos+sin2xsin=cos(2x–),
所以函数f(x)的最小正周期T==π.
(2)因为f(α)=,且f(β)=,
所以cos(2α–)=,cos(2β–)=.
又<α<β<,所以2α–,2β–∈(0,),
所以sin(2α–)==,
sin(2β–)==,
所以cos(2β–2α)
=cos[(2β–)–(2α–)]
=cos(2β–)·cos(2α–)+sin(2β–)sin(2α–)
=×+×
=.
又<α<β<,所以0<2β–2α<,所以2β–2α=.
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.cos15°的值是
A. B.
C. D.
2.已知,则=
A.7 B.–7
C. D.
3.cos(35°+x)cos(55°–x)–sin(35°+x)sin(55°–x)的值是
A.0 B.–1
C.±1 D.1
4.设α∈(0,2π),已知sin α>cos α,则α的取值范围是
A.() B.(,π)
C.() D.()
5.已知=
A. B.–3
C. D.3
6.已知点A(cos80°,sin80°),B(cos20°,sin20°),则||等于
A. B.
C. D.1
7.已知锐角α,β满足sin α=,cos β=,则α+β等于
A. B.或
C. D.2kπ+(k∈Z)
8.函数f(x)=cos2x–2cos2(x∈[0,π])的最小值为
A.1 B.–1
C. D.
9.下列是函数f(x)=sinxcosxcos2x+的零点的是
A. B.π
C. D.
10.函数f(x)=(1+cos2x)·sin2x(x∈R)是
A.最小正周期为π的奇函数 B.最小正周期为的奇函数
C.最小正周期为π的偶函数 D.最小正周期为的偶函数
11.已知α,β∈(,),tanα,tanβ是方程x2+12x+10=0的两根,则tan=
A. B.–2或
C. D.–2
12.定义运算/=ad–bc,若cosα=/,/=/,0<β<αA./ B./
C./ D./
二、填空题:请将答案填在题中横线上.
13.已cosθ=,则cos2θ=__________.
14.–2cos10°=___________.
15.已知,则=__________.
16.已知,,则tan(α+β)=__________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(1)化简.
(2)已知α∈(0,π),且cos(α–)=.求cosα.
18.已知sinα=,且α为第二象限角.
(1)求sin2α的值;
(2)求tan(α+)的值.
19.已知tan(α+)=–3.
(1)求tanα的值;
(2)求sin(2α–)的值.
20.求证:–2cos(x+y)=.
21.在△ABC中,sinA=sinBtanA,且B为钝角.
(1)证明:B–A=;
(2)求sinA+sinC的取值范围.
22.已知函数f(x)=–cos2xcos+sin2xsin.
(1)求函数f(x)的最小正周期;
(2)若<α<β<,f(α)=,且f(β)=,求角2β–2α的大小.
参考答案
1
2
3
4
5
6
7
8
9
10
11
12
D
D
A
C
B
D
C
D
D
D
D
D
1.【答案】D
【解析】cos15°=cos(45°–30°)=cos45°cos30°+sin45°sin30°=×+×=,故选D.
2.【答案】D
【解析】由得,,所以=,故选D.
3.【答案】A
【解析】cos(35°+x)cos(55°–x)–sin(35°+x)sin(55°–x)=cos[(35°+x)+(55°–x)]=cos90°=0,故选A.
4.【答案】C
【解析】(1)解法一:因为sin α–cos α>0,即sin α–cos α>0,所以sin(α–)>0,所以2kπ<α–<2kπ+π,k∈Z,所以2kπ+<α<2kπ+,k∈Z,又α∈(0,2π),所以α∈().故选C.
解法二:取α=π,因为sin π=0,cos π=–,则sin π>cos π,符合题意,排除A,B;取α=,因为sin=–,=–,则sin=,不符合题意,排除D.故选C.
5.【答案】B
【解析】由cos(+α)=2cos(π–α),可得–sinα=–2cosα,所以tanα=2,
则tan=–3.故选B.
6.【答案】D
【解析】||==
===1.
7.【答案】C
【解析】由sin α=,cos β=,且α,β为锐角,知cos α=,sin β=,故cos(α+β)=cos αcos β–sin αsin β=×– ×=,又0<α+β<π,故α+β=.
8.【答案】D
【解析】由题意,得f(x)=cos2x–2cos2=cos2x–(1+cosx)=cos2x–cosx–1,设t=cosx(x∈[0,π]),y=f(x),则t∈[–1,1],y=t2–t–1=(t)2,所以当t=,即x=时,y取得最小值,为,所以函数f(x)的最小值为,故选D.
9.【答案】D
【解析】f(x)=sinxcosxcos2x+=sin2x(1+cos2x)+=sin(2x),令sin(2x)=0,得2x=kπ,k∈Z,所以x=+,k∈Z,当k=1时,x=.故选D.
10.【答案】D
【解析】由题意,得f(x)=(1+cos2x)(1–cos2x)=(1–cos22x)=sin22x=(1–cos4x).又f(–x)=f(x),所以函数f(x)是最小正周期为的偶函数,选D.
11.【答案】D
【解析】∵α,β∈(,),tanα,tanβ是方程x2+12x+10=0的两根,∴tanα+tanβ=–12,tanα·tanβ=10,∴tanα<0,tanβ<0,∴<α<0,<β<0,∴<<0.又tan(α+β)====,整理得2tan2+3tan2=0,解得tan=–2或tan=(舍去),故选D.
12.【答案】D
【解析】依题意有/=sinαcosβ–cosαsinβ=sin(α–β)=/.∵0<β<α13.【答案】–
【解析】由二倍角的余弦公式可得cos2θ=2cos2θ–1=2×–1=–,故答案为:–.
14.【答案】
【解析】–2cos10°=
=
=.故答案为:.
15.【答案】–
【解析】∵,∴,解得tan,因此,=tanα–=–.故答案为:–.
16.【答案】–
【解析】,∴cosαcos–sinαsincosα,∴–sinα=cosα,∴tanα==–.又,∴tan(α+β)==–.故答案为:–.
17.【解析】(1)=
===.
(2)∵α∈(0,π),∴,
又,
∴,
∴
.
18.【解析】(1)∵sinα=,且α为第二象限角,∴cos,
∴sin2α=2sinαcosα=;
(2)由(1)知tan,∴tan(α+)=.
19.【解析】(1)∵tan(α+)=–3,
∴tanα=tan(α+–)=,
(2)∵sin2α=,
cos2α==–,
∴sin(2α–)=sin2α?cos–cos2α?sin=+.
20.【解析】左边=–2cos(x+y)
=–2cos(x+y)
=
=
==右边.
∴原等式成立.
21.【解析】(1)由sinA=sinBtanA,得=,
所以sinB=cosA,即sinB=sin(+A).
又B为钝角,因此+A∈(,π),故B=+A,即B–A=.
(2)由(1),知C=π–(A+B)=–2A>0,所以A∈(0,).
于是sinA+sinC=sinA+sin(–2A)=sinA+cos2A=–2sin2A+sinA+1=–2(sinA–)2+.
因为0
即sinA+sinC的取值范围是(,].
22.【解析】(1)因为f(x)=–cos2xcos+sin2xsin,
所以f(x)=cos2xcos+sin2xsin=cos(2x–),
所以函数f(x)的最小正周期T==π.
(2)因为f(α)=,且f(β)=,
所以cos(2α–)=,cos(2β–)=.
又<α<β<,所以2α–,2β–∈(0,),
所以sin(2α–)==,
sin(2β–)==,
所以cos(2β–2α)
=cos[(2β–)–(2α–)]
=cos(2β–)·cos(2α–)+sin(2β–)sin(2α–)
=×+×
=.
又<α<β<,所以0<2β–2α<,所以2β–2α=.
