人教版2018_2019学年八年级数学上册第十一章三角形11.3多边形及其内角和作业设计含答案
文档属性
| 名称 | 人教版2018_2019学年八年级数学上册第十一章三角形11.3多边形及其内角和作业设计含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 86.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-28 00:00:00 | ||
图片预览

文档简介
11.3 多边形及其内角和
选择题
1.若一个多边形的内角和小于其外角和,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
2.一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形 B.正八边形 C.正十边形 D.正十二边形
3.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6 C.5或7 D.5或6或7
4.如图,小林从点P向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
A.30° B.40° C.80° D.不存在
(第4题图)
5.若从一个多边形的一个顶点出发,最多可以引9条对角线,则它是( )
A.十三边形 B.十二边形 C.十一边形 D.十边形
6.若一个多边形共有20条对角线,则它是( )
A.六边形 B.七边形 C.八边形 D.九边形
7.内角和等于外角和2倍的多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
8.一个多边形的外角中,钝角的个数不可能是( )
A.1个 B.2个 C.3个 D.4个
9.一个多边形的内角中,锐角的个数最多有( )
A.3个 B.4个 C.5个 D.6个
10.若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( )
A.90° B.105° C.130° D.120°
11.一个多边形截去一个角后,所形成的一个多边形的内角和是2520°,那么原多边形的边数是( )
A.15 B.16 C.17 D.15或16或17
12.下列说法正确的是 ( )
每条边相等的多边形是正多边形 B. 每个内角相等的多边形是正多边形
C. 每条边相等且每个内角相等的多边形是正多边形 D.以上说法都对
13.正多边形的一个内角的度数不可能是( )
A.80° B.135° C.144° D.150°
14.多边形的边数增加1,则它的内角和( )
A.不变 B.增加180° C.增加360° D.无法确定
15.在四边形中,、、、的度数之比为2∶3∶4∶3,则的外角等于( )
A.60° B.75° C.90° D.120°?
二、填空题
16.每个内角都为135°的多边形为_________边形.
17.一个多边形的每一个外角都等于15°,这个多边形是________边形.
18.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为9:2,则这个多边形的边数为_________.
19.多边形的内角和与其一个外角的度数总和为1300°,则这个外角的度数为________.
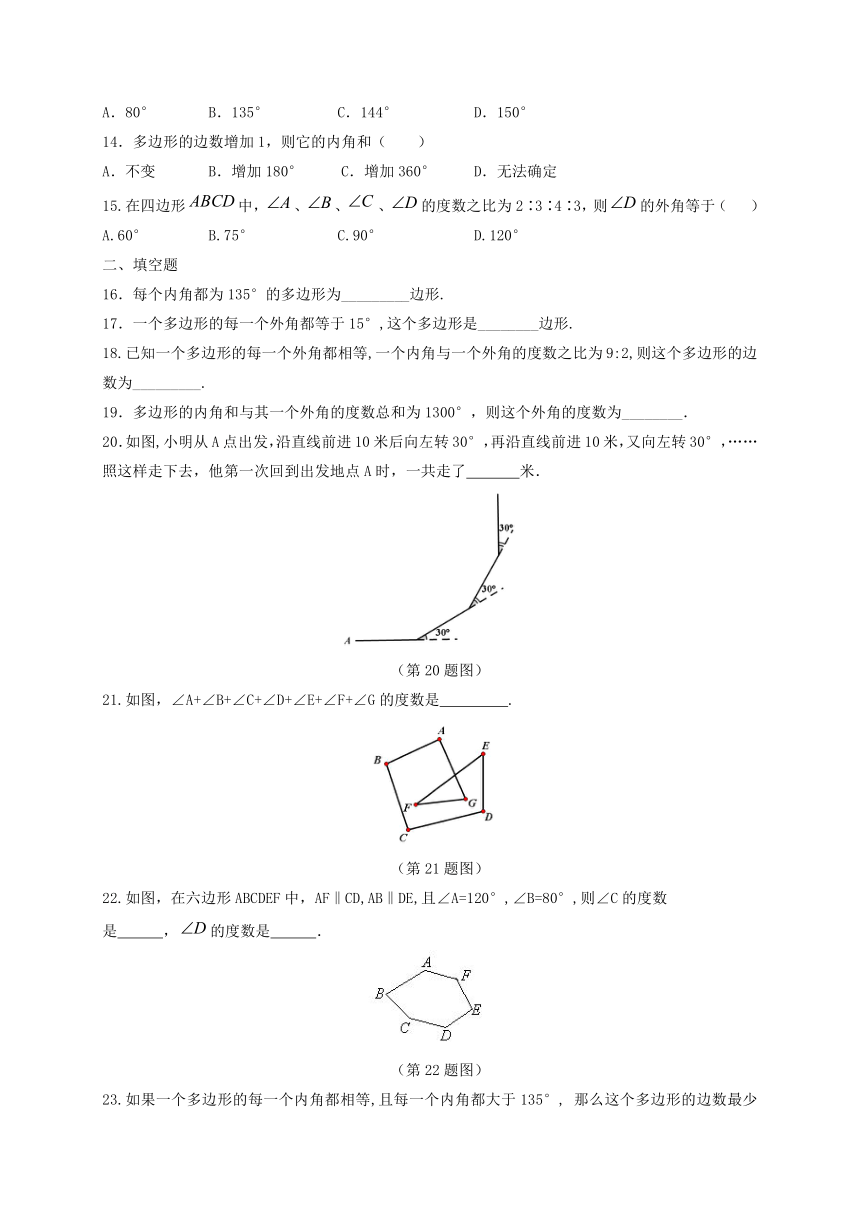
20.如图,小明从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,……照这样走下去,他第一次回到出发地点A时,一共走了 米.
(第20题图)
21.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数是 .
(第21题图)
22.如图,在六边形ABCDEF中,AF‖CD,AB‖DE,且∠A=120°,∠B=80°,则∠C的度数
是 ,的度数是 .
(第22题图)
23.如果一个多边形的每一个内角都相等,且每一个内角都大于135°, 那么这个多边形的边数最少为________.
24.如果一个多边形的每一个外角都是锐角,那么这个多边形的边数最小是___________.
三、解答题
25.一个正多边形的一个内角的度数比相邻外角的6倍还多12°,求这个正多边形的内角和.
26.如果两个多边形的边数之比为1:2,那么这两个多边形的内角之和为1440°,请你确定这两个多边形的边数.
27.用几何画板工具可以很方便地画出正五角星(如图1所示).
(1) 图1中 .
(2)拖动点到图2和图3的位置时, 的值是否发生变化?说明你的理由.
图1 图2 图3
(第27题图)
28.如图,在四边形ABDE中,∠B,∠D的平分线交于点C,试探究∠A,∠E,∠C之间的关系.
(第28题图)
参考答案
一、1.A 2.C 3.D 4.B 5.B 6.C 7.B 8.D 9.A 10.C 11.D 12.C 13.A
14.B 15.C
二、16.八 17.二十四 18. 11 19. 40° 20. 120 21. 540°
160°120°23.9 24.5
三、25.解:设这个正多边形的一个外角的度数为x.
根据题意,得x+6x+12°=180°,解得x=24°,
所以这个正多边形的边数为=15,
其内角和为(15-2)×180°=2340°.
26.解:设其中一个多边形的边数为n,则另一个多边形的边数为2n.
根据题意得:(n-2)?180°+(2n-2)?180°=1440°,
解得n=4.
2n=8.
故这两个多边形的边数分别为4,8.
27.解:(1)180°. (2)不变,理由略.
28.解:因为∠ABD+∠BDE=360°-(∠A+∠E),所以∠DBC+∠BDC=180°-(∠A+∠E).
因为∠C=180°-(∠DBC+∠BDC),所以∠C=(∠A+∠E).
30°
30°
30°
A
30°
30°
30°
A
PAGE
选择题
1.若一个多边形的内角和小于其外角和,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
2.一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形 B.正八边形 C.正十边形 D.正十二边形
3.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6 C.5或7 D.5或6或7
4.如图,小林从点P向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
A.30° B.40° C.80° D.不存在
(第4题图)
5.若从一个多边形的一个顶点出发,最多可以引9条对角线,则它是( )
A.十三边形 B.十二边形 C.十一边形 D.十边形
6.若一个多边形共有20条对角线,则它是( )
A.六边形 B.七边形 C.八边形 D.九边形
7.内角和等于外角和2倍的多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
8.一个多边形的外角中,钝角的个数不可能是( )
A.1个 B.2个 C.3个 D.4个
9.一个多边形的内角中,锐角的个数最多有( )
A.3个 B.4个 C.5个 D.6个
10.若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( )
A.90° B.105° C.130° D.120°
11.一个多边形截去一个角后,所形成的一个多边形的内角和是2520°,那么原多边形的边数是( )
A.15 B.16 C.17 D.15或16或17
12.下列说法正确的是 ( )
每条边相等的多边形是正多边形 B. 每个内角相等的多边形是正多边形
C. 每条边相等且每个内角相等的多边形是正多边形 D.以上说法都对
13.正多边形的一个内角的度数不可能是( )
A.80° B.135° C.144° D.150°
14.多边形的边数增加1,则它的内角和( )
A.不变 B.增加180° C.增加360° D.无法确定
15.在四边形中,、、、的度数之比为2∶3∶4∶3,则的外角等于( )
A.60° B.75° C.90° D.120°?
二、填空题
16.每个内角都为135°的多边形为_________边形.
17.一个多边形的每一个外角都等于15°,这个多边形是________边形.
18.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为9:2,则这个多边形的边数为_________.
19.多边形的内角和与其一个外角的度数总和为1300°,则这个外角的度数为________.
20.如图,小明从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,……照这样走下去,他第一次回到出发地点A时,一共走了 米.
(第20题图)
21.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数是 .
(第21题图)
22.如图,在六边形ABCDEF中,AF‖CD,AB‖DE,且∠A=120°,∠B=80°,则∠C的度数
是 ,的度数是 .
(第22题图)
23.如果一个多边形的每一个内角都相等,且每一个内角都大于135°, 那么这个多边形的边数最少为________.
24.如果一个多边形的每一个外角都是锐角,那么这个多边形的边数最小是___________.
三、解答题
25.一个正多边形的一个内角的度数比相邻外角的6倍还多12°,求这个正多边形的内角和.
26.如果两个多边形的边数之比为1:2,那么这两个多边形的内角之和为1440°,请你确定这两个多边形的边数.
27.用几何画板工具可以很方便地画出正五角星(如图1所示).
(1) 图1中 .
(2)拖动点到图2和图3的位置时, 的值是否发生变化?说明你的理由.
图1 图2 图3
(第27题图)
28.如图,在四边形ABDE中,∠B,∠D的平分线交于点C,试探究∠A,∠E,∠C之间的关系.
(第28题图)
参考答案
一、1.A 2.C 3.D 4.B 5.B 6.C 7.B 8.D 9.A 10.C 11.D 12.C 13.A
14.B 15.C
二、16.八 17.二十四 18. 11 19. 40° 20. 120 21. 540°
160°120°23.9 24.5
三、25.解:设这个正多边形的一个外角的度数为x.
根据题意,得x+6x+12°=180°,解得x=24°,
所以这个正多边形的边数为=15,
其内角和为(15-2)×180°=2340°.
26.解:设其中一个多边形的边数为n,则另一个多边形的边数为2n.
根据题意得:(n-2)?180°+(2n-2)?180°=1440°,
解得n=4.
2n=8.
故这两个多边形的边数分别为4,8.
27.解:(1)180°. (2)不变,理由略.
28.解:因为∠ABD+∠BDE=360°-(∠A+∠E),所以∠DBC+∠BDC=180°-(∠A+∠E).
因为∠C=180°-(∠DBC+∠BDC),所以∠C=(∠A+∠E).
30°
30°
30°
A
30°
30°
30°
A
PAGE
