人教版数学五年级下册4.4.1《求两个数最大公因数的实际应用》教案(表格版)
文档属性
| 名称 | 人教版数学五年级下册4.4.1《求两个数最大公因数的实际应用》教案(表格版) |
|
|
| 格式 | zip | ||
| 文件大小 | 35.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-28 17:15:49 | ||
图片预览

文档简介
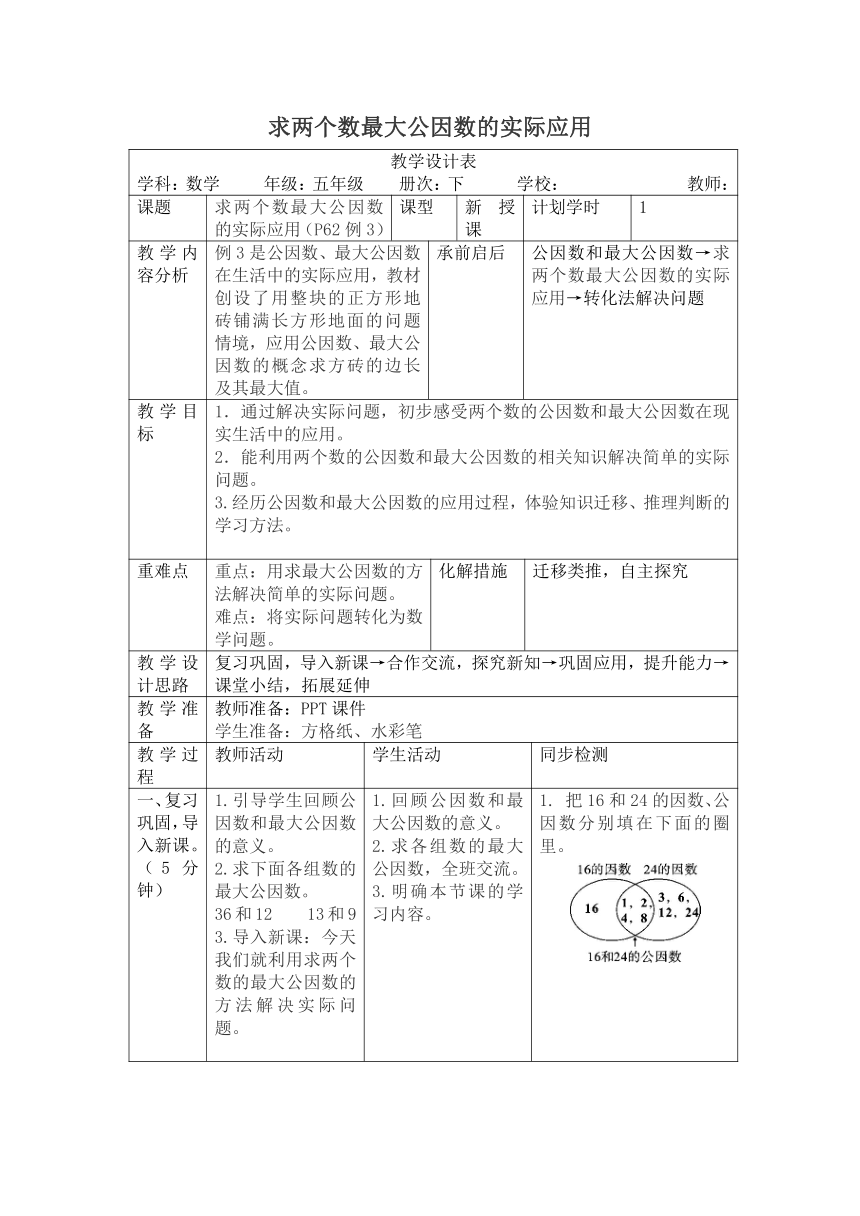
求两个数最大公因数的实际应用
教学设计表
学科:数学 年级:五年级 册次:下 学校: 教师:
课题
求两个数最大公因数的实际应用(P62例3)
课型
新授课
计划学时
1
教学内容分析
例3是公因数、最大公因数在生活中的实际应用,教材创设了用整块的正方形地砖铺满长方形地面的问题情境,应用公因数、最大公因数的概念求方砖的边长及其最大值。
承前启后
公因数和最大公因数→求两个数最大公因数的实际应用→转化法解决问题
教学目标
1.通过解决实际问题,初步感受两个数的公因数和最大公因数在现实生活中的应用。
2.能利用两个数的公因数和最大公因数的相关知识解决简单的实际问题。
3.经历公因数和最大公因数的应用过程,体验知识迁移、推理判断的学习方法。
重难点
重点:用求最大公因数的方法解决简单的实际问题。
难点:将实际问题转化为数学问题。
化解措施
迁移类推,自主探究
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
学生准备:方格纸、水彩笔
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.引导学生回顾公因数和最大公因数的意义。
2.求下面各组数的最大公因数。
36和12 13和9
3.导入新课:今天我们就利用求两个数的最大公因数的方法解决实际问题。
1.回顾公因数和最大公因数的意义。
2.求各组数的最大公因数,全班交流。
3.明确本节课的学习内容。
?
1. 把16和24的因数、公因数分别填在下面的圈里。
/
二、合作交流,探究新知。(20分钟)
1.明确要求。
(1) 课件出示教材第62页例3,引导学生理解“整分米数”和“整块”的意义。
(2)引导学生思考:在铺地面时,有时剩余的部分放不下1整块地砖,就要把地砖进行切割,这样做是否符合要求?
2.动手操作。
(1)组织学生讨论选择地砖的方法。
(2)引导学生动手操作,在方格纸上画一画。
3.概括方法。
(1)组织学生汇报操作结果。
(2)讨论:要满足用整块地砖铺满地面的要求,地砖的边长必须符合什么条件。
4.知识拓展。
(1)组织学生阅读教材第64页“你知道吗?”
(2)引导学生说一说什么是互质数。
1.(1) 认真观察情境图,讨论交流“整分米数”和“整块”的意义。
(2)根据“整块”的意义说明切割的地砖不符合要求。
2.(1)小组讨论选择地砖的方法。
(2)动手操作,在方格纸上画一画,然后选出符合条件的地砖。
3.(1)交流后各自说出操作结果。
(可以选择边长是1 dm、2 dm、4 dm的地砖,最大可以选择边长是4 dm的地砖)
(2)小组合作讨论:要满足用整块地砖铺满地面的要求,地砖的边长必须是12和16的公因数。
4.阅读教材第64页“你知道吗?”的内容,理解互质数的意义。
/3.王阿姨准备用一张长40 cm、宽30 cm的长方形纸板剪出若干个大小相同的正方形。剪出的正方形的边长最长是多少厘米?一共可以剪出多少个这样的正方形?(正方形的边长是整厘米数,并且纸板没有剩余)
因为40和30的最大公因数是10,所以剪出的正方形的边长最长是10 cm。
(40÷10)×(30÷10)=12(个)
可以剪出12个这样的正方形。
三、巩固应用,提升能力。(10分钟)
1.完成教材第63页第5题。
2.完成教材第63页第6题。
1.读题,分析题意并独立解答,同桌交流答案。
2.独立完成,全班订正。
4.互质的两个数一定都是质数吗?
不一定
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.查阅资料,了解《几何原本》这一数学巨著。
教师个人补充意见:
板书设计
求两个数最大公因数的实际应用
12的因数:1,2,3,4,6,12。
16的因数:1,2,4,8,16。
12和16的公因数有1,2,4,其中最大公因数是4。
可以选择边长是1 dm、2 dm、4 dm的地砖,最大可以选择边长是4 dm的地砖。
培优作业
张老师给全班同学带来一些糖果。若把110块糖果平均分给同学们,则多5块;若把210块糖果平均分给同学们,则正好分完;若把240块糖果平均分给同学们,则少5块。张老师的班级最多有多少名同学?
105,210和245的最大公因数是35,因此张老师的班级最多有35名同学。
教学反思
教学时,在培养学生初步的逻辑思维能力的同时,也要有意识地培养学生的发散思维。因此,要鼓励学生交流不同的想法和解题方法,采取多种形式的训练培养学生思维的敏捷性和灵活性,以达到培养发散思维的目的。
微课设计点
教师可围绕“求两个数最大公因数的实际应用”设计微课。
教学设计表
学科:数学 年级:五年级 册次:下 学校: 教师:
课题
求两个数最大公因数的实际应用(P62例3)
课型
新授课
计划学时
1
教学内容分析
例3是公因数、最大公因数在生活中的实际应用,教材创设了用整块的正方形地砖铺满长方形地面的问题情境,应用公因数、最大公因数的概念求方砖的边长及其最大值。
承前启后
公因数和最大公因数→求两个数最大公因数的实际应用→转化法解决问题
教学目标
1.通过解决实际问题,初步感受两个数的公因数和最大公因数在现实生活中的应用。
2.能利用两个数的公因数和最大公因数的相关知识解决简单的实际问题。
3.经历公因数和最大公因数的应用过程,体验知识迁移、推理判断的学习方法。
重难点
重点:用求最大公因数的方法解决简单的实际问题。
难点:将实际问题转化为数学问题。
化解措施
迁移类推,自主探究
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
学生准备:方格纸、水彩笔
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.引导学生回顾公因数和最大公因数的意义。
2.求下面各组数的最大公因数。
36和12 13和9
3.导入新课:今天我们就利用求两个数的最大公因数的方法解决实际问题。
1.回顾公因数和最大公因数的意义。
2.求各组数的最大公因数,全班交流。
3.明确本节课的学习内容。
?
1. 把16和24的因数、公因数分别填在下面的圈里。
/
二、合作交流,探究新知。(20分钟)
1.明确要求。
(1) 课件出示教材第62页例3,引导学生理解“整分米数”和“整块”的意义。
(2)引导学生思考:在铺地面时,有时剩余的部分放不下1整块地砖,就要把地砖进行切割,这样做是否符合要求?
2.动手操作。
(1)组织学生讨论选择地砖的方法。
(2)引导学生动手操作,在方格纸上画一画。
3.概括方法。
(1)组织学生汇报操作结果。
(2)讨论:要满足用整块地砖铺满地面的要求,地砖的边长必须符合什么条件。
4.知识拓展。
(1)组织学生阅读教材第64页“你知道吗?”
(2)引导学生说一说什么是互质数。
1.(1) 认真观察情境图,讨论交流“整分米数”和“整块”的意义。
(2)根据“整块”的意义说明切割的地砖不符合要求。
2.(1)小组讨论选择地砖的方法。
(2)动手操作,在方格纸上画一画,然后选出符合条件的地砖。
3.(1)交流后各自说出操作结果。
(可以选择边长是1 dm、2 dm、4 dm的地砖,最大可以选择边长是4 dm的地砖)
(2)小组合作讨论:要满足用整块地砖铺满地面的要求,地砖的边长必须是12和16的公因数。
4.阅读教材第64页“你知道吗?”的内容,理解互质数的意义。
/3.王阿姨准备用一张长40 cm、宽30 cm的长方形纸板剪出若干个大小相同的正方形。剪出的正方形的边长最长是多少厘米?一共可以剪出多少个这样的正方形?(正方形的边长是整厘米数,并且纸板没有剩余)
因为40和30的最大公因数是10,所以剪出的正方形的边长最长是10 cm。
(40÷10)×(30÷10)=12(个)
可以剪出12个这样的正方形。
三、巩固应用,提升能力。(10分钟)
1.完成教材第63页第5题。
2.完成教材第63页第6题。
1.读题,分析题意并独立解答,同桌交流答案。
2.独立完成,全班订正。
4.互质的两个数一定都是质数吗?
不一定
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.查阅资料,了解《几何原本》这一数学巨著。
教师个人补充意见:
板书设计
求两个数最大公因数的实际应用
12的因数:1,2,3,4,6,12。
16的因数:1,2,4,8,16。
12和16的公因数有1,2,4,其中最大公因数是4。
可以选择边长是1 dm、2 dm、4 dm的地砖,最大可以选择边长是4 dm的地砖。
培优作业
张老师给全班同学带来一些糖果。若把110块糖果平均分给同学们,则多5块;若把210块糖果平均分给同学们,则正好分完;若把240块糖果平均分给同学们,则少5块。张老师的班级最多有多少名同学?
105,210和245的最大公因数是35,因此张老师的班级最多有35名同学。
教学反思
教学时,在培养学生初步的逻辑思维能力的同时,也要有意识地培养学生的发散思维。因此,要鼓励学生交流不同的想法和解题方法,采取多种形式的训练培养学生思维的敏捷性和灵活性,以达到培养发散思维的目的。
微课设计点
教师可围绕“求两个数最大公因数的实际应用”设计微课。
