人教版数学五年级下册4.5.1《最小公倍数》教案(表格版)
文档属性
| 名称 | 人教版数学五年级下册4.5.1《最小公倍数》教案(表格版) |
|
|
| 格式 | zip | ||
| 文件大小 | 20.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-28 17:19:49 | ||
图片预览

文档简介
最小公倍数
教学设计表
学科:数学 年级:五年级 册次:下 学校: 教师:
课题
最小公倍数(P68例1、P69例2)
课型
新授课
计划学时
1
教学内容分析
例1列举了4和6的倍数,从中找出它们公有的倍数及其中最小的倍数,引出公倍数、最小公倍数的概念。例2教学求两个数的最小公倍数的方法,主要采用“找”的方法,降低了难度,符合学生学习的实际需要。
承前启后
因数和倍数→公倍数和最小公倍数→通分
教学目标
1.理解公倍数、最小公倍数的意义。
2.掌握求两个数的最小公倍数的方法,会求两个数的最小公倍数。
3.在学习过程中,培养学生的学习兴趣,养成良好的学习习惯。
重难点
重点:理解公倍数和最小公倍数的概念。
难点:掌握求两个数的最小公倍数的方法。
化解措施
迁移类推,归纳概括
教学设计思路
复习旧知,引入新课→探究意义,建构概念→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习旧知,引入新课。(5分钟)
1.复习。
出示问题:说一说4和6的倍数分别有哪些。
2.导入。
师:我们分别列出了4的倍数和6的倍数。前面我们已经学过两个数公有的因数,今天来学习两个数公有的倍数。
1.分别找4和6的倍数。
4的倍数:4,8,12,16,20,…
6的倍数:6,12,18,24,30,…
2.明确本节课的学习内容。
1.找一找。
60 18 680 3 6 12 9 24 36 2 1
6的倍数:(60,18,6,12,24,36)
6的因数:(3,6,2,1)
二、探究意义,建构概念。(20分钟)
1. 探究概念。
(1)引导学生在数轴上分别找出表示4的倍数和6的倍数的点。
(2)引导学生观察数轴,思考:4和6公有的倍数有哪些?最小的是几?有没有最大的?
(3)迁移命名。
师:想一想我们已经学过的公因数和最大公因数,谁能给公有的倍数和其中最小的一个取名字?
(4)引导学生说一说公倍数和最小公倍数的意义。
(5)集合表示法。
课件出示教材第68页的集合圈。提问:为什么集合圈里要写上省略号?
2.教学最小公倍数的求法。
(1)组织学生用多种方法找6和8的最小公倍数。
(2)出示几组数,引导学生找出各组数的最小公倍数,观察并发现规律。
2和3 12和36
5和7 8和12?
23和45? 7和14?
3.引导学生自学教材第69页“你知道吗?”。
4.优化方法,师生共同归纳最小公倍数的求法。
1.(1)用两种不同颜色的笔在数轴上分别描点。
(2)观察数轴,交流发现,汇报:4和6公有的倍数有12,24,36,…最小的是12,没有最大的。
(3)迁移公因数和最大公因数的知识,尝试命名。(公倍数、最小公倍数)
(4)口答:几个数公有的倍数叫作这几个数的公倍数,其中最小的一个叫作它们的最小公倍数。
(5)讨论交流后明确:因为一个数的倍数的个数是无限的,几个数的公倍数的个数也是无限的,所以要写上省略号。
2.(1)分别用列举法、筛选法等不同的方法找6和8的最小公倍数。
(2)找出每组数的最小公倍数。
发现规律:两个数是互质关系的,它们的最小公倍数就是它们的乘积;两个数是倍数关系的,它们的最小公倍数就是较大的那个数。
3.自学用分解质因数法、短除法求两个数的最小公倍数。
4.结合前面的学习过程,讨论交流,明确求最小公倍数的方法。
2.填空。
(1) 9和15的最小公倍数是(45)。
(2)最小的合数与最大的一位数的最小公倍数是(36)。
(3)a和b只有公因数1(a,b都是不为0的自然数),a和b的最小公倍数是(ab)。
(4)a=2×3×5,b=2×3×5×7,a和b的最小公倍数是(210)。
(5)a÷b=c(a,b都是不为0的自然数),a和b的最小公倍数是(a)。
3.求下面每组数的最小公倍数。
(1)36和24
72
(2)22和33
66
(3)16和28?
112
(4)26和39?
78
(5)9和10?
90
(6)19和57
57
三、巩固应用,提升能力。(10分钟)
1.完成教材第71页第1,2题。
2.完成教材第71页第7题。
1. 独立完成,全班交流订正。
2.先独立思考,再交流自己是怎样思考的,完成后集体订正。
4. 两个数的最大公因数是7,最小公倍数是28,这两个数是(7和28)。
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.用短除法求最大公因数或最小公倍数时,除的过程相同,除数相乘所得的积是最大公因数,除数与所得的商相乘所得的积是最小公倍数。
教师个人补充意见:
板书设计
最小公倍数
4的倍数:4,8,12,16,20,24,28,32,36,40,…
6的倍数:6,12,18,24,30,36,42,…
12,24,36,…是4和6公有的倍数,叫作它们的公倍数。其中,12是最小的公倍数,叫作它们的最小公倍数。
公倍数和最小公倍数之间的关系:两个数的公倍数是它们的最小公倍数的整数倍。
培优作业
两个数的最大公因数是15,最小公倍数是90,求这两个数分别是多少。
假设这两个数分别是a和b。
/
15a1b1=90 a1b1=90÷15=6=1×6=2×3。
当a1,b1分别是1和6时,a,b分别为15×1=15,15×6=90;当a1,b1分别是2和3时,a,b分别为15×2=30,15×3=45。
因此这两个数分别是15和90或30和45。
教学反思
教学时,要注重角色转变,改变在以往的教学中只注重对学生知识的传授,而忽略了学生的主观能动性的教学方法,要让学生学会自主学习,让学生主动参与课堂教学,在教学中尊重学生,凸显学生的主体地位。
微课设计点
教师可围绕“最小公倍数的求法”设计微课。
教学设计表
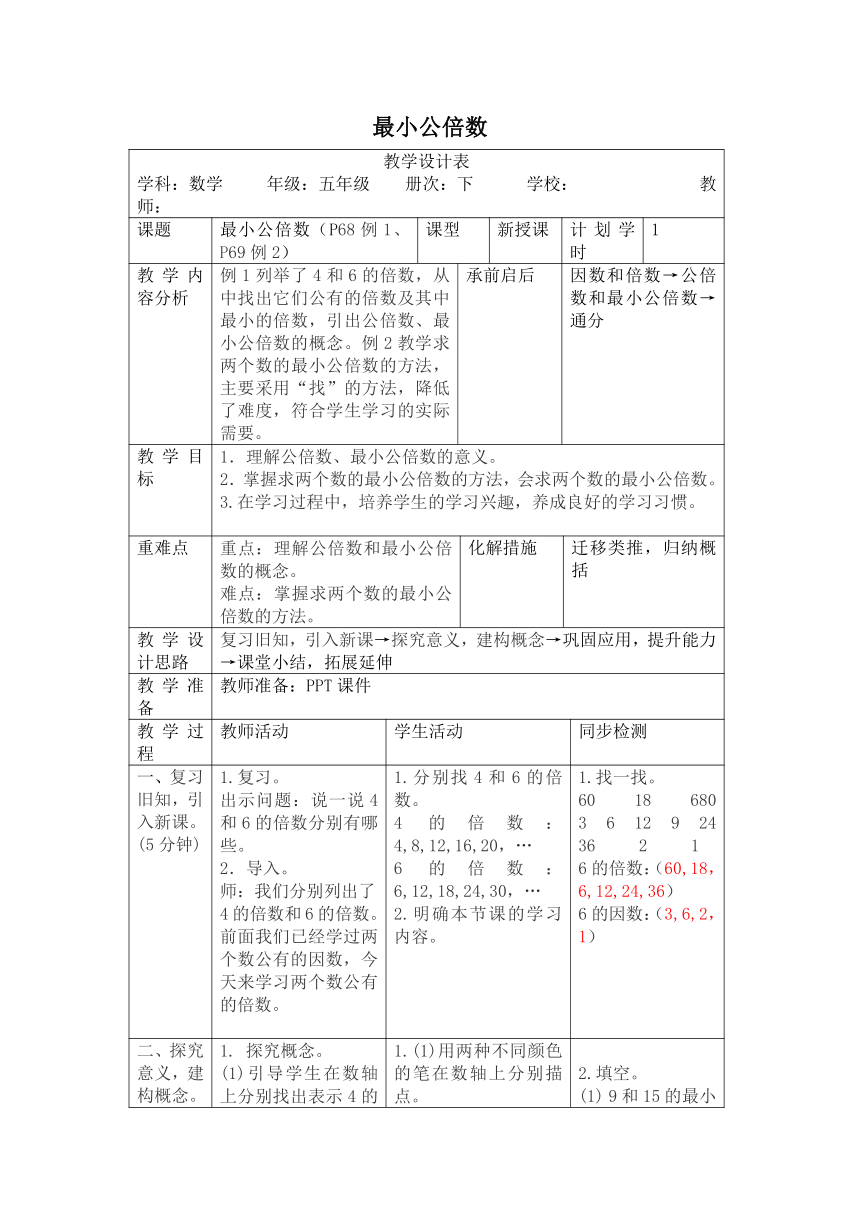
学科:数学 年级:五年级 册次:下 学校: 教师:
课题
最小公倍数(P68例1、P69例2)
课型
新授课
计划学时
1
教学内容分析
例1列举了4和6的倍数,从中找出它们公有的倍数及其中最小的倍数,引出公倍数、最小公倍数的概念。例2教学求两个数的最小公倍数的方法,主要采用“找”的方法,降低了难度,符合学生学习的实际需要。
承前启后
因数和倍数→公倍数和最小公倍数→通分
教学目标
1.理解公倍数、最小公倍数的意义。
2.掌握求两个数的最小公倍数的方法,会求两个数的最小公倍数。
3.在学习过程中,培养学生的学习兴趣,养成良好的学习习惯。
重难点
重点:理解公倍数和最小公倍数的概念。
难点:掌握求两个数的最小公倍数的方法。
化解措施
迁移类推,归纳概括
教学设计思路
复习旧知,引入新课→探究意义,建构概念→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习旧知,引入新课。(5分钟)
1.复习。
出示问题:说一说4和6的倍数分别有哪些。
2.导入。
师:我们分别列出了4的倍数和6的倍数。前面我们已经学过两个数公有的因数,今天来学习两个数公有的倍数。
1.分别找4和6的倍数。
4的倍数:4,8,12,16,20,…
6的倍数:6,12,18,24,30,…
2.明确本节课的学习内容。
1.找一找。
60 18 680 3 6 12 9 24 36 2 1
6的倍数:(60,18,6,12,24,36)
6的因数:(3,6,2,1)
二、探究意义,建构概念。(20分钟)
1. 探究概念。
(1)引导学生在数轴上分别找出表示4的倍数和6的倍数的点。
(2)引导学生观察数轴,思考:4和6公有的倍数有哪些?最小的是几?有没有最大的?
(3)迁移命名。
师:想一想我们已经学过的公因数和最大公因数,谁能给公有的倍数和其中最小的一个取名字?
(4)引导学生说一说公倍数和最小公倍数的意义。
(5)集合表示法。
课件出示教材第68页的集合圈。提问:为什么集合圈里要写上省略号?
2.教学最小公倍数的求法。
(1)组织学生用多种方法找6和8的最小公倍数。
(2)出示几组数,引导学生找出各组数的最小公倍数,观察并发现规律。
2和3 12和36
5和7 8和12?
23和45? 7和14?
3.引导学生自学教材第69页“你知道吗?”。
4.优化方法,师生共同归纳最小公倍数的求法。
1.(1)用两种不同颜色的笔在数轴上分别描点。
(2)观察数轴,交流发现,汇报:4和6公有的倍数有12,24,36,…最小的是12,没有最大的。
(3)迁移公因数和最大公因数的知识,尝试命名。(公倍数、最小公倍数)
(4)口答:几个数公有的倍数叫作这几个数的公倍数,其中最小的一个叫作它们的最小公倍数。
(5)讨论交流后明确:因为一个数的倍数的个数是无限的,几个数的公倍数的个数也是无限的,所以要写上省略号。
2.(1)分别用列举法、筛选法等不同的方法找6和8的最小公倍数。
(2)找出每组数的最小公倍数。
发现规律:两个数是互质关系的,它们的最小公倍数就是它们的乘积;两个数是倍数关系的,它们的最小公倍数就是较大的那个数。
3.自学用分解质因数法、短除法求两个数的最小公倍数。
4.结合前面的学习过程,讨论交流,明确求最小公倍数的方法。
2.填空。
(1) 9和15的最小公倍数是(45)。
(2)最小的合数与最大的一位数的最小公倍数是(36)。
(3)a和b只有公因数1(a,b都是不为0的自然数),a和b的最小公倍数是(ab)。
(4)a=2×3×5,b=2×3×5×7,a和b的最小公倍数是(210)。
(5)a÷b=c(a,b都是不为0的自然数),a和b的最小公倍数是(a)。
3.求下面每组数的最小公倍数。
(1)36和24
72
(2)22和33
66
(3)16和28?
112
(4)26和39?
78
(5)9和10?
90
(6)19和57
57
三、巩固应用,提升能力。(10分钟)
1.完成教材第71页第1,2题。
2.完成教材第71页第7题。
1. 独立完成,全班交流订正。
2.先独立思考,再交流自己是怎样思考的,完成后集体订正。
4. 两个数的最大公因数是7,最小公倍数是28,这两个数是(7和28)。
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.用短除法求最大公因数或最小公倍数时,除的过程相同,除数相乘所得的积是最大公因数,除数与所得的商相乘所得的积是最小公倍数。
教师个人补充意见:
板书设计
最小公倍数
4的倍数:4,8,12,16,20,24,28,32,36,40,…
6的倍数:6,12,18,24,30,36,42,…
12,24,36,…是4和6公有的倍数,叫作它们的公倍数。其中,12是最小的公倍数,叫作它们的最小公倍数。
公倍数和最小公倍数之间的关系:两个数的公倍数是它们的最小公倍数的整数倍。
培优作业
两个数的最大公因数是15,最小公倍数是90,求这两个数分别是多少。
假设这两个数分别是a和b。
/
15a1b1=90 a1b1=90÷15=6=1×6=2×3。
当a1,b1分别是1和6时,a,b分别为15×1=15,15×6=90;当a1,b1分别是2和3时,a,b分别为15×2=30,15×3=45。
因此这两个数分别是15和90或30和45。
教学反思
教学时,要注重角色转变,改变在以往的教学中只注重对学生知识的传授,而忽略了学生的主观能动性的教学方法,要让学生学会自主学习,让学生主动参与课堂教学,在教学中尊重学生,凸显学生的主体地位。
微课设计点
教师可围绕“最小公倍数的求法”设计微课。
