北师大版2020年中考总复习资料,补习复习资料:58动手操作与运动变换型问题(基础)含答案
文档属性
| 名称 | 北师大版2020年中考总复习资料,补习复习资料:58动手操作与运动变换型问题(基础)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 702.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-28 20:39:27 | ||
图片预览




文档简介
中考冲刺:动手操作与运动变换型问题—知识讲解(基础)
【中考展望】
1.对于实践操作型问题,在解题过程中学生能够感受到数学学习的情趣与价值,经历“数学化”和“再创造”的过程,不断提高自己的创新意识与综合能力,这是《全日制义务教育数学课程标准(实验稿)》的基本要求之一,因此,近年来实践操作性试题受到命题者的重视,多次出现.
2.估计在今年的中考题中,实践操作类题目依旧是出题热点,仍符合常规题型,与三角形的全等和四边形的性质综合考查.需具备一定的分析问题能力和归纳推理能力.
图形的设计与操作问题,主要分为如下一些类型:
1.已知设计好的图案,求设计方案(如:在什么基本图案的基础上,进行何种图形变换等).
2.利用基本图案设计符合要求的图案(如:设计轴对称图形,中心对称图形,面积或形状符合特定要求的图形等).
3.图形分割与重组(如:通过对原图形进行分割、重组,使形状满足特定要求).
4.动手操作(通过折叠、裁剪等手段制作特定图案).
解决这样的问题,除了需要运用各种基本的图形变换(平移、轴对称、旋转、位似)外,还需要综合运用代数、几何知识对图形进行分析、计算、证明,以获得重要的数据,辅助图案设计.
另外,由于折叠操作相当于构造轴对称变换,因此折叠问题中,要充分利用轴对称变换的特性,以获得更多的图形信息.必要时,实际动手配合上理论分析比单纯的理论分析更为快捷有效.
从历年中考来看,动态问题经常作为压轴题目出现,得分率也是最低的.动态问题一般分两类,一类是代数综合题,在坐标系中有动点,动直线,一般是利用多种函数交叉求解.另一类就是几何综合题,在梯形,矩形,三角形中设立动点、线以及整体平移翻转,对考生的综合分析能力进行考查.所以说,动态问题是中考数学当中的重中之重,只有完全掌握,才有机会拼高分.
【方法点拨】
实践操作问题:
解答实践操作题的关键是要学会自觉地运用数学知识去观察、分析、抽象、概括所给的实际问题,揭示其数学本质,并转化为我们所熟悉的数学问题.解答实践操作题的基本步骤为:从实例或实物出发,通过具体操作实验,发现其中可能存在的规律,提出问题,检验猜想.在解答过程中一般需要经历操作、观察、思考、想象、推理、探索、发现、总结、归纳等实践活动过程,利用自己已有的生活经验和数学知识去感知发生的现象,从而发现所得到的结论,进而解决问题.
动态几何问题:
1、动态几何常见类型
(1)点动问题(一个动点)
(2)线动问题(二个动点)
(3)面动问题(三个动点)
2、运动形式
平移、旋转、翻折、滚动
3、数学思想
函数思想、方程思想、分类思想、转化思想、数形结合思想
4、解题思路
(1)化动为静,动中求静
(2)建立联系,计算说明
(3)特殊探路,一般推证
【典型例题】
类型一、图形的折叠
/1.如图所示,一个平行四边形纸片ABCD中,E,F分别为BC,CD边上的点,将纸片沿AE,EF折叠,使B,C的对应点B′,C′及点E在同一直线上,则∠AEF=________.
/
【思路点拨】
纸片沿AE折叠,折叠前后的两个图形关于直线AE对称,所以△AEB与△AEB′全等,对应角相等.同理沿EF折叠的两个三角形的对应角也相等.
【答案】∠AEF=90°.
【解析】
解: 由轴对称的性质,知∠AEB=∠AEB′,∠CEF=∠C′EF,
而∠AEB+∠AEB′+∠CEF+∠C′EF=180°.
所以∠AEF-∠AEB′+∠C′EF=90°.
【总结升华】
图形的折叠实质上就是轴对称的一种变形应用.解题时应抓住折叠前后的图形全等找出对应关系.
举一反三:
【变式】如图所示,已知四边形纸片ABCD,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线最多有两条,能否做到:________ (用“能”或“不能”填空).若填“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.
/
【答案】
解:能.如图所示,取四边形ABCD各边的中点E,F,G,H,连接EG,FH,交点为O.
/
以EG,FH为裁剪线,EG,FH将四边形ABCD分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四部分,拼接时图中的Ⅰ不动,将Ⅱ,Ⅳ分别绕E,H旋转180°,将Ⅲ平移,拼成的四边形OO1O2O3即为所求.沿CA方向平移,将点C平移到点A位置.
类型二、实践操作
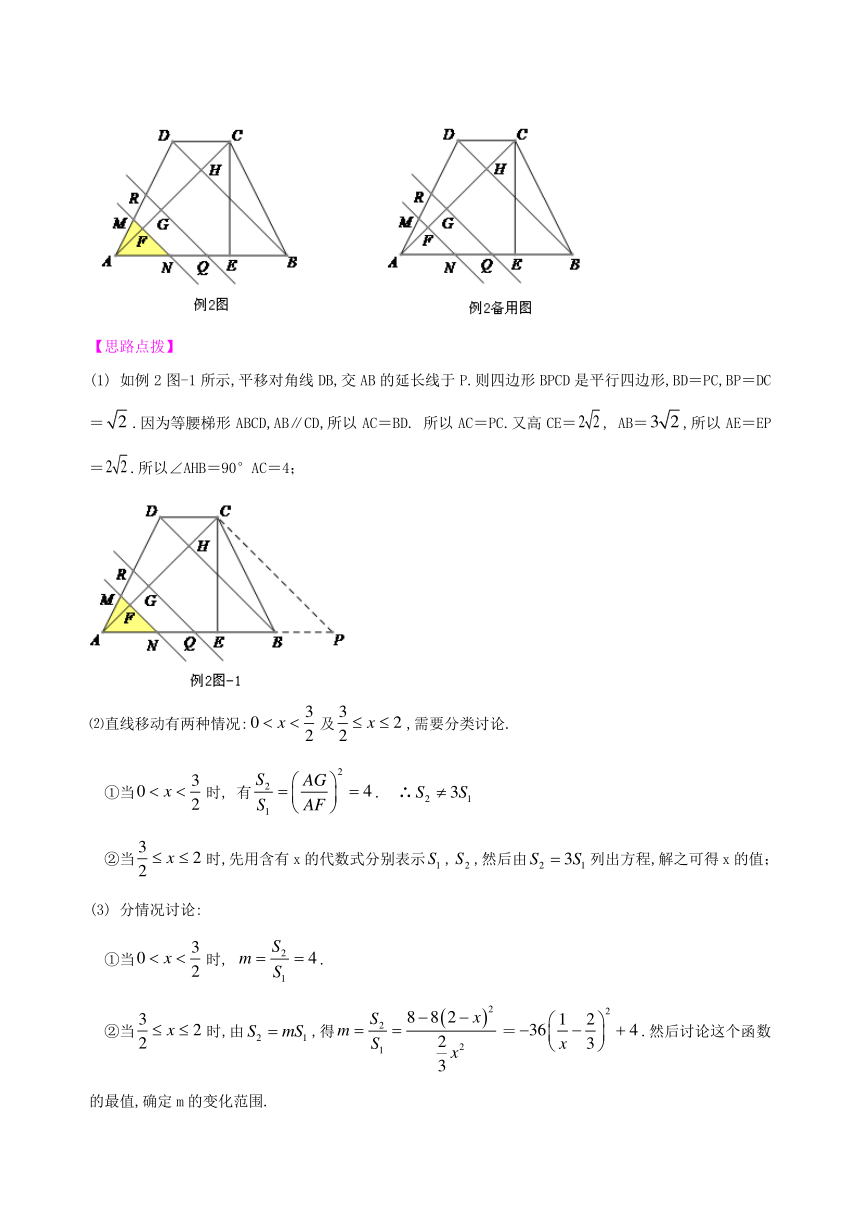
/2.如图,在等腰梯形ABCD中AB∥CD,AB=/,DC=/,高CE=/,对角线AC、BD交于H,平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G;当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的面积为/,被直线RQ扫过的面积为/,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
(1)填空:∠AHB=____________;AC=_____________;
(2) 若/,求x;
(3) 若/,求m的变化范围.
/
【思路点拨】
(1) 如例2图-1所示,平移对角线DB,交AB的延长线于P.则四边形BPCD是平行四边形,BD=PC,BP=DC=/.因为等腰梯形ABCD,AB∥CD,所以AC=BD. 所以AC=PC.又高CE=/, AB=/,所以AE=EP=/.所以∠AHB=90°AC=4;
/
⑵直线移动有两种情况:/及/,需要分类讨论.
①当/时, 有/. ∴/
②当/时,先用含有x的代数式分别表示/,/,然后由/列出方程,解之可得x的值; (3) 分情况讨论:
①当/时, /.
②当/时,由/,得/=/.然后讨论这个函数的最值,确定m的变化范围.
【答案与解析】
解: (1) 90°,4;
(2)直线移动有两种情况:/和/.
①当/时,∵MN∥BD,∴△AMN∽△ARQ,△ANF∽△AQG.
/. ∴/
②当/时, 如例2图-2所示,
/
CG=4-2x,CH=1,/. /
/,/
由/,得方程/,
解得/(舍去),/.
∴x=2.
(3) 当/时,m=4
当/时,
由/,得/=/=/.
M是/的二次函数, 当/时, 即当/时, M随/的增大而增大.
当/时,最大值m=4. 当x=2时,最小值m=3.
∴3≤m≤4.
【总结升华】
本题是一道几何代数综合压轴题,重点考查等腰梯形, 相似三角形的性质,二次函数的增减性和最值及分类讨论,由特殊到一般的数学思想等的综合应用.解题时,
(1)小题,通过平移对角线,将等腰梯形转化为等腰三角形,从而使问题得以简化,是我们解决梯形问题常用的方法.
(2) 小题直线移动有两种情况:/及/,需要分类讨论.这点万不可忽略,解题时用到的知识点主要是相似三角形面积比等于相似比的平方.
(3) 小题仍需要分情况讨论.对于函数/,讨论它的增减性和最值是个难点. 讨论之前点明我们把这个函数看作“M是/的二次函数”对顺利作答至关重要.
/3.已知等边三角形纸片ABC的边长为8,D为AB边上的点,过点D作DG∥BC交AC于点G,DE⊥BC于点E,过点G作GF⊥BC于点F,把三角形纸片ABC分别沿DG、DE、GF按图①所示方式折叠.点A、B、C分别落在A′、B′、C′处.若点A′、B′、C′在矩形DEFG内或其边上.且互不重合,此时我们称/ (即图中阴影部分)为“重叠三角形”.
/
(1)若把三角形纸片ABC放在等边三角形网格图中(图中每个小三角形都是边长为l的等边三角形),点A、B、C、D恰好落在网格图中的格点上,如图②所示,请直接写出此时重叠三角形A′B′C′的面积;
(2)实验探究:设AD的长为m,若重叠三角形A′B′C′存在,试用含m的代数式表示重叠三角形A′B′C′的面积,并写出m的取值范围(直接写出结果,备用图供实验探究使用).
/
【思路点拨】
本题是折叠与对称类型操作题,折叠实质为对称变换,故轴对称的性质运用是解本类型题的关键.另外,本题对新概念“重叠三角形”的理解正确才能求得m的取值范围.
【答案与解析】
解:(1)重叠三角形A′B′C′的面积为/.
理由:如题图,△A′B′C′是边长为2的等边三角形.
∴其高为/,面积为/.
(2)用含m的代数式表示重叠三角形A′B′C′的面积为/,m的取值范围是/≤m<4.
理由:如图(1),AD=m,则BD=GC=8-m,
由轴对称的性质知DB′=DB=8-m.DA′=DA=m.
∴A′B′=DB′-DA′=8-m—m=2(4-m),
由△ABC是等边三角形及折叠过程知AA′B′C′是等边三角形.
∴它的高是/.
/.
以下求m的取值范围:
如图(1),若B′与F重合,则C′与E重合.
/
由折叠过程知BE=EB′=EF.
CF=FC′=FE.∴BE=EF=FC=/.
∵∠B=60°,BD=2BE=/,
/,即/.
若/,如图(2),点B′、C′落在矩形DEFG外,不合题意.
/
∴/.
又由A′B′=2(4-m)>0,得m<4.
∴m的取值范围是/.
【总结升华】亲自操作实验有助于突破难点.
举一反三:
【图形的设计与操作及运动变换型问题 例2 】
【变式】阅读下面问题的解决过程:
问题:已知△ABC中,P为BC边上一定点,过点P作一直线,使其等分△ABC的面积.
解决:情形1:如图①,若点P恰为BC的中点,作直线AP即可.
情形2:如图②,若点P不是BC的中点,则取BC的中点D,联结AP,过点D作DE∥AP交AC于E,作直线PE,直线PE即为所求直线.
/
问题解决:
如图③,已知四边形ABCD,过点B作一直线(不必写作法),使其等分四边形ABCD的面积,并证明.
/
【答案】
解:如图③,取对角线AC的中点O,联结BO、DO、BD, 过点O作OE∥BD交CD于E, ∴直线BE即为所求直线
/
类型三、动态数学问题
/4.如图①,有一张矩形纸片,将它沿对角线AC剪开,得到△ACD和△A′BC′.
(1)如图②,将△ACD沿A′C′边向上平移,使点A与点C′重合,连接A′D和BC,四边形A′BCD是 形;
(2)如图③,将△ACD的顶点A与A′点重合,然后绕点A沿逆时针方向旋转,使点D、A、B在同一直线上,则旋转角为 度;连接CC′,四边形CDBC′是 形;
(3)如图④,将AC边与A′C′边重合,并使顶点B和D在AC边的同一侧,设AB、CD相交于E,连接BD,四边形ADBC是什么特殊四边形?请说明你的理由.
/
【思路点拨】
(1)利用平行四边形的判定,对角线互相平分的四边形是平行四边形得出即可;(2)利用旋转变换的性质以及直角梯形判定得出即可;(3)利用等腰梯形的判定方法得出BD∥AC,AD=CE,即可得出答案.
【答案与解析】
解:(1)平行四边形;
证明:∵AD=AB,AA′=AC,∴A′C与BD互相平分,
∴四边形A′BCD是平行四边形;
(2)∵DA由垂直于AB,逆时针旋转到点D、A、B在同一直线上,
∴旋转角为90度;
证明:∵∠D=∠B=90°,A,D,B在一条直线上,
∴CD∥BC′,∴四边形CDBC′是直角梯形;
故答案为:90,直角梯;
/
(3)四边形ADBC是等腰梯形;
证明:过点B作BM⊥AC,过点D作DN⊥AC,垂足分别为M,N,
∵有一张矩形纸片,将它沿对角线AC剪开,得到△ACD和△A′BC′.∴△ACD≌△A′BC′,
∴BM=ND,∴BD∥AC,
∵AD=BC,∴四边形ADBC是等腰梯形.
【总结升华】
此题主要考查了图形的剪拼与平行四边形的判定和等腰梯形的判定、直角梯形的判定方法等知识,熟练掌握判定定理是解题关键.
举一反三:
【图形的设计与操作及运动变换型问题 例1 】
【变式】△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点O为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1∶2,则线段AC的中点P变换后对应的点的坐标为______.
【答案】(/)或(/).
/5.如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位:cm2)与点P移动的时间(单位:s)的函数如图②所示,则点P从开始移动到停止移动一共用了 秒(结果保留根号).
/
【思路点拨】
根据图②判断出AB、BC的长度,过点B作BE⊥AD于点E,然后求出梯形ABCD的高BE,再根据t=2时△PAD的面积求出AD的长度,过点C作CF⊥AD于点F,然后求出DF的长度,利用勾股定理列式求出CD的长度,然后求出AB、BC、CD的和,再根据时间=路程÷速度,计算即可得解.
【答案】(4+2/).
【解析】
解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,
∴在AB上运动的时间是2秒,在BC上运动的时间是4-2=2秒,
∵动点P的运动速度是1cm/s,
∴AB=2cm,BC=2cm,
过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,
则四边形BCFE是矩形,
∴BE=CF,BC=EF=2cm,
∵∠A=60°,
∴BE=ABsin60°=2×/=/,
AE=ABcos60°=2×/=1,
∴/×AD×BE=3/,
即/×AD×/=3/,
解得AD=6cm,
∴DF=AD-AE-EF=6-1-2=3,
在Rt△CDF中,CD=/=/=2/,
所以,动点P运动的总路程为AB+BC+CD=2+2+2/=4+2/,
∵动点P的运动速度是1cm/s,
∴点P从开始移动到停止移动一共用了(4+2/)÷1=4+2/(秒).
故答案为:(4+2/).
/
【总结升华】
本题考查了动点问题的函数图象,根据图②的三角形的面积的变化情况判断出AB、BC的长度是解题的关键,在梯形的问题中,作过梯形的上底边的两个顶点的高线是常见的辅助线.
中考冲刺:动手操作与运动变换型问题—巩固练习(基础)
【巩固练习】
一、选择题
1. 如图,在Rt△ABC 中,∠C=90° ,AC=BC=6cm,点P从点A出发,沿AB方向以每秒/cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间t秒,若四边形QPCP为菱形,则t的值为( )
A. / B. 2 C. / D.3
2.如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t的值为( )
A. / B. 1 C. /或1 D. /或1或/
/ /
3. 如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为( )
/
/
二、填空题
4.如图,已知点A(0,2)、B(/,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连结AP,以AP为边在其左侧作等边△APQ ,连结PB、BA.若四边形ABPQ为梯形,则(1)当AB为梯形的底时,点P的横坐标是 ;(2)当AB为梯形的腰时,点P的横坐标是 .
/
5.如图,矩形纸片ABCD,AB=2,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好落在AC上,则AC的长是 .
/
6.如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是 .
三、解答题
7.如图所示是规格为8×8的正方形网格,请在所给网格中,按下列要求操作:
/
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点的坐标是________,△ABC的周长是________ (结果保留根号);
(3)画出△ABC以点C为旋转中心、旋转180°后的△A′B′C,连接AB′和A′B,试说出四边形/是何特殊四边形,并说明理由.
8. (1)观察与发现
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.
(2)实践与运用
将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.
/
9. 如图(1),已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角形板DEF绕D点按逆时针方向旋转.
(1)在图(1)中,DE交AB于M,DF交BC于N.
①证明:DM=ND;
②在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的;若不发生变化,求出其面积;
(2)继续旋转至如图(2)所示的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)继续旋转至如图(3)所示的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?若成立,请写出结论,不用证明.
/
10. 如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.
(1)试证明:无论点.P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的/?
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形?
/
【答案与解析】
一、选择题 1.【答案】B;
【解析】连接PP′交BC于点D,若四边形QPCP为菱形,则PP′⊥BC,CD=/CQ=/(6-t),
∴BD=6-/(6-t)=3+/t.在Rt△BPD中,PB=AB-AP=6/-/t,而PB=/BD,
∴6/-/t=/(3+/t),解得:t=2,故选B.
2.【答案】D;
【解析】∵AB是⊙O的直径,∴∠ACB=90°;Rt△ABC中,BC=2,∠ABC=60°; ∴AB=2BC=4cm.①当∠BFE=90°时;Rt△BEF中,∠ABC=60°,
则BE=2BF=2cm;故此时AE=AB-BE=2cm;∴E点运动的距离为:2cm或6cm,
故t=1s或3s;由于0≤t<3,故t=3s不合题意,舍去;所以当∠BFE=90°时,t=1s;②当∠BEF=90°时;同①可求得BE=0.5cm,此时AE=AB-BE=3.5cm;∴E点运动的距离为:3.5cm或4.5cm,故t=1.75s或2.25s;综上所述,当t的值为1、1.75或2.25s时,△BEF是直角三角形.故选D.
3.【答案】B.
【解析】在0≤x≤4时,y随x的增大而减小,在4≤x≤8时,y随x的增大而增大;且y与x的函数关系是二次函数,故选B.
二、填空题
4.【答案】(1)/;(2)0, /;
【解析】(1)由题意知,当AB为梯形的底时,AB∥PQ,即PQ⊥y轴,又△APQ为等边三角形,AC=2,由几何关系知,点P的横坐标是/.(2)当AB为梯形的腰时,当PB∥y轴时,满足题意,此时AQ=4,由几何关系得,点P的横坐标是/.
/ /
5.【答案】4;
【解析】由折叠可知∠BAE=∠CAE,因为AE=EC所以∠CAE=∠ACE,所以∠BAE=∠CAE=∠ACE,
三角的和为90°,所以∠ACE=30°,所以AC=2AB=4.
6.【答案】①④⑤.
【解析】由折叠知:∠ADG=∠GDO根据外角定理∠AGD=∠GDO+∠GOD而∠GOD=90°,
∠GDO = /∠ADO=22.5°得∠AGD=112.5°所以①正确.
由折叠知△AGD≌△FGD得S△AGD=S△FGD所以③错误.
∠AED=90°-22.5°=67.5°,∠AGE=45°+22.5°=67.5°故∠AED=∠AGE可得AE=AG,
易证AG=FG,AE=EF,从而得AG=FG=AE=EF.所以④正确.
BE=/EF,EF= FG=/OG,故BE=2OG所以⑤正确.
AE= FG=/OG,AD= AB=AE+ BE=(/+2)OG,在Rt△AED中tan∠AED=/=/,所以②错误.
三、解答题
7.【答案与解析】
(1)如图所示建立平面直角坐标系.
/
(2)如图画出点C,C(-1,1).△ABC的周长是/.
(3)如图画出△A′B′C,四边形ABA′B′是矩形.
理由:∵CA=CA′,CB=CB′,
∴四边形ABA′B′是平行四边形.
又∵CA=CB,
∴CA=CA′=CB=CB′.
∴AA′=BB′.
∴四边形ABA′B′是矩形.
8.【答案与解析】
解:(1)同意.
如图所示,设AD与EF交于点G.
/
由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.
又由折叠知,∠AGE=∠AGF=90°,
所以∠AEF=∠AFE,
所以AE=AF,即△AEF为等腰三角形.
(2)由折叠知,四边形ABFE是正方形∠AEB=45°,
所以∠BED=135°.
又由折叠知,∠BEG=∠DEG,
所以∠DEG=67.5°.
从而∠α=90°-67.5°=22.5°.
9.【答案与解析】
解:(1)①连接DB,利用△BMD≌△CND或△ADM∽△BDN即可证明DM=DN.
②由△BMD≌△CND知,/,
∴/.
即在直角三角板DEF旋转过程中,四边形DMBN的面积始终等于/,不发生变化.
/
(2)连接DB,由△BMD≌△CND可证明DM=DN,即DM=DN仍然成立.
(3)连接DB.由△BMD≌△CND,可证明DM=ND仍成立.
10.【答案与解析】
解:(1)证明:在正方形ABCD中,无论点P运动到AB上何处时,
都有AD=AB,∠DAQ=∠BAQ,AQ=AQ,∴△ADQ≌△ABQ.
(2)解:假设下图中△ADQ的面积恰好是正方形ABCD面积的/.
/
过点Q作QE⊥AD于E,QF⊥AB于F,则QE=QF,
/.
∴/.
由△DEQ∽△DAP得/,解得AP=2.
∴AP=2时,△ADQ的面积是正方形ABCD面积的/.
(3)若△ADQ是等腰三角形,则有DQ=QA或DA=DQ或AQ=AD.
①当点P运动到与点B重合时,由四边形ABCD是正方形知QD=QA,此时△ADQ是等腰三角形.
②当点P与点C重合时,点Q与点C也重合,此时DA=DQ,△ADQ是等腰三角形.
③如图所示,设点P在BC边上运动到CP=x时,有AD=AQ.
/
∵AD∥BC,∴∠ADQ=∠CPQ.
又∵∠AQD=∠CQP,∠ADQ=∠AQD,
∴∠CQP=∠CPQ.
∴CQ=CP=x.
∵AC=/,AQ=QD=4,
∴x=CQ=AC-AQ=/,
即当CP=/时,△ADQ是等腰三角形.
【中考展望】
1.对于实践操作型问题,在解题过程中学生能够感受到数学学习的情趣与价值,经历“数学化”和“再创造”的过程,不断提高自己的创新意识与综合能力,这是《全日制义务教育数学课程标准(实验稿)》的基本要求之一,因此,近年来实践操作性试题受到命题者的重视,多次出现.
2.估计在今年的中考题中,实践操作类题目依旧是出题热点,仍符合常规题型,与三角形的全等和四边形的性质综合考查.需具备一定的分析问题能力和归纳推理能力.
图形的设计与操作问题,主要分为如下一些类型:
1.已知设计好的图案,求设计方案(如:在什么基本图案的基础上,进行何种图形变换等).
2.利用基本图案设计符合要求的图案(如:设计轴对称图形,中心对称图形,面积或形状符合特定要求的图形等).
3.图形分割与重组(如:通过对原图形进行分割、重组,使形状满足特定要求).
4.动手操作(通过折叠、裁剪等手段制作特定图案).
解决这样的问题,除了需要运用各种基本的图形变换(平移、轴对称、旋转、位似)外,还需要综合运用代数、几何知识对图形进行分析、计算、证明,以获得重要的数据,辅助图案设计.
另外,由于折叠操作相当于构造轴对称变换,因此折叠问题中,要充分利用轴对称变换的特性,以获得更多的图形信息.必要时,实际动手配合上理论分析比单纯的理论分析更为快捷有效.
从历年中考来看,动态问题经常作为压轴题目出现,得分率也是最低的.动态问题一般分两类,一类是代数综合题,在坐标系中有动点,动直线,一般是利用多种函数交叉求解.另一类就是几何综合题,在梯形,矩形,三角形中设立动点、线以及整体平移翻转,对考生的综合分析能力进行考查.所以说,动态问题是中考数学当中的重中之重,只有完全掌握,才有机会拼高分.
【方法点拨】
实践操作问题:
解答实践操作题的关键是要学会自觉地运用数学知识去观察、分析、抽象、概括所给的实际问题,揭示其数学本质,并转化为我们所熟悉的数学问题.解答实践操作题的基本步骤为:从实例或实物出发,通过具体操作实验,发现其中可能存在的规律,提出问题,检验猜想.在解答过程中一般需要经历操作、观察、思考、想象、推理、探索、发现、总结、归纳等实践活动过程,利用自己已有的生活经验和数学知识去感知发生的现象,从而发现所得到的结论,进而解决问题.
动态几何问题:
1、动态几何常见类型
(1)点动问题(一个动点)
(2)线动问题(二个动点)
(3)面动问题(三个动点)
2、运动形式
平移、旋转、翻折、滚动
3、数学思想
函数思想、方程思想、分类思想、转化思想、数形结合思想
4、解题思路
(1)化动为静,动中求静
(2)建立联系,计算说明
(3)特殊探路,一般推证
【典型例题】
类型一、图形的折叠
/1.如图所示,一个平行四边形纸片ABCD中,E,F分别为BC,CD边上的点,将纸片沿AE,EF折叠,使B,C的对应点B′,C′及点E在同一直线上,则∠AEF=________.
/
【思路点拨】
纸片沿AE折叠,折叠前后的两个图形关于直线AE对称,所以△AEB与△AEB′全等,对应角相等.同理沿EF折叠的两个三角形的对应角也相等.
【答案】∠AEF=90°.
【解析】
解: 由轴对称的性质,知∠AEB=∠AEB′,∠CEF=∠C′EF,
而∠AEB+∠AEB′+∠CEF+∠C′EF=180°.
所以∠AEF-∠AEB′+∠C′EF=90°.
【总结升华】
图形的折叠实质上就是轴对称的一种变形应用.解题时应抓住折叠前后的图形全等找出对应关系.
举一反三:
【变式】如图所示,已知四边形纸片ABCD,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线最多有两条,能否做到:________ (用“能”或“不能”填空).若填“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.
/
【答案】
解:能.如图所示,取四边形ABCD各边的中点E,F,G,H,连接EG,FH,交点为O.
/
以EG,FH为裁剪线,EG,FH将四边形ABCD分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四部分,拼接时图中的Ⅰ不动,将Ⅱ,Ⅳ分别绕E,H旋转180°,将Ⅲ平移,拼成的四边形OO1O2O3即为所求.沿CA方向平移,将点C平移到点A位置.
类型二、实践操作
/2.如图,在等腰梯形ABCD中AB∥CD,AB=/,DC=/,高CE=/,对角线AC、BD交于H,平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G;当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的面积为/,被直线RQ扫过的面积为/,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
(1)填空:∠AHB=____________;AC=_____________;
(2) 若/,求x;
(3) 若/,求m的变化范围.
/
【思路点拨】
(1) 如例2图-1所示,平移对角线DB,交AB的延长线于P.则四边形BPCD是平行四边形,BD=PC,BP=DC=/.因为等腰梯形ABCD,AB∥CD,所以AC=BD. 所以AC=PC.又高CE=/, AB=/,所以AE=EP=/.所以∠AHB=90°AC=4;
/
⑵直线移动有两种情况:/及/,需要分类讨论.
①当/时, 有/. ∴/
②当/时,先用含有x的代数式分别表示/,/,然后由/列出方程,解之可得x的值; (3) 分情况讨论:
①当/时, /.
②当/时,由/,得/=/.然后讨论这个函数的最值,确定m的变化范围.
【答案与解析】
解: (1) 90°,4;
(2)直线移动有两种情况:/和/.
①当/时,∵MN∥BD,∴△AMN∽△ARQ,△ANF∽△AQG.
/. ∴/
②当/时, 如例2图-2所示,
/
CG=4-2x,CH=1,/. /
/,/
由/,得方程/,
解得/(舍去),/.
∴x=2.
(3) 当/时,m=4
当/时,
由/,得/=/=/.
M是/的二次函数, 当/时, 即当/时, M随/的增大而增大.
当/时,最大值m=4. 当x=2时,最小值m=3.
∴3≤m≤4.
【总结升华】
本题是一道几何代数综合压轴题,重点考查等腰梯形, 相似三角形的性质,二次函数的增减性和最值及分类讨论,由特殊到一般的数学思想等的综合应用.解题时,
(1)小题,通过平移对角线,将等腰梯形转化为等腰三角形,从而使问题得以简化,是我们解决梯形问题常用的方法.
(2) 小题直线移动有两种情况:/及/,需要分类讨论.这点万不可忽略,解题时用到的知识点主要是相似三角形面积比等于相似比的平方.
(3) 小题仍需要分情况讨论.对于函数/,讨论它的增减性和最值是个难点. 讨论之前点明我们把这个函数看作“M是/的二次函数”对顺利作答至关重要.
/3.已知等边三角形纸片ABC的边长为8,D为AB边上的点,过点D作DG∥BC交AC于点G,DE⊥BC于点E,过点G作GF⊥BC于点F,把三角形纸片ABC分别沿DG、DE、GF按图①所示方式折叠.点A、B、C分别落在A′、B′、C′处.若点A′、B′、C′在矩形DEFG内或其边上.且互不重合,此时我们称/ (即图中阴影部分)为“重叠三角形”.
/
(1)若把三角形纸片ABC放在等边三角形网格图中(图中每个小三角形都是边长为l的等边三角形),点A、B、C、D恰好落在网格图中的格点上,如图②所示,请直接写出此时重叠三角形A′B′C′的面积;
(2)实验探究:设AD的长为m,若重叠三角形A′B′C′存在,试用含m的代数式表示重叠三角形A′B′C′的面积,并写出m的取值范围(直接写出结果,备用图供实验探究使用).
/
【思路点拨】
本题是折叠与对称类型操作题,折叠实质为对称变换,故轴对称的性质运用是解本类型题的关键.另外,本题对新概念“重叠三角形”的理解正确才能求得m的取值范围.
【答案与解析】
解:(1)重叠三角形A′B′C′的面积为/.
理由:如题图,△A′B′C′是边长为2的等边三角形.
∴其高为/,面积为/.
(2)用含m的代数式表示重叠三角形A′B′C′的面积为/,m的取值范围是/≤m<4.
理由:如图(1),AD=m,则BD=GC=8-m,
由轴对称的性质知DB′=DB=8-m.DA′=DA=m.
∴A′B′=DB′-DA′=8-m—m=2(4-m),
由△ABC是等边三角形及折叠过程知AA′B′C′是等边三角形.
∴它的高是/.
/.
以下求m的取值范围:
如图(1),若B′与F重合,则C′与E重合.
/
由折叠过程知BE=EB′=EF.
CF=FC′=FE.∴BE=EF=FC=/.
∵∠B=60°,BD=2BE=/,
/,即/.
若/,如图(2),点B′、C′落在矩形DEFG外,不合题意.
/
∴/.
又由A′B′=2(4-m)>0,得m<4.
∴m的取值范围是/.
【总结升华】亲自操作实验有助于突破难点.
举一反三:
【图形的设计与操作及运动变换型问题 例2 】
【变式】阅读下面问题的解决过程:
问题:已知△ABC中,P为BC边上一定点,过点P作一直线,使其等分△ABC的面积.
解决:情形1:如图①,若点P恰为BC的中点,作直线AP即可.
情形2:如图②,若点P不是BC的中点,则取BC的中点D,联结AP,过点D作DE∥AP交AC于E,作直线PE,直线PE即为所求直线.
/
问题解决:
如图③,已知四边形ABCD,过点B作一直线(不必写作法),使其等分四边形ABCD的面积,并证明.
/
【答案】
解:如图③,取对角线AC的中点O,联结BO、DO、BD, 过点O作OE∥BD交CD于E, ∴直线BE即为所求直线
/
类型三、动态数学问题
/4.如图①,有一张矩形纸片,将它沿对角线AC剪开,得到△ACD和△A′BC′.
(1)如图②,将△ACD沿A′C′边向上平移,使点A与点C′重合,连接A′D和BC,四边形A′BCD是 形;
(2)如图③,将△ACD的顶点A与A′点重合,然后绕点A沿逆时针方向旋转,使点D、A、B在同一直线上,则旋转角为 度;连接CC′,四边形CDBC′是 形;
(3)如图④,将AC边与A′C′边重合,并使顶点B和D在AC边的同一侧,设AB、CD相交于E,连接BD,四边形ADBC是什么特殊四边形?请说明你的理由.
/
【思路点拨】
(1)利用平行四边形的判定,对角线互相平分的四边形是平行四边形得出即可;(2)利用旋转变换的性质以及直角梯形判定得出即可;(3)利用等腰梯形的判定方法得出BD∥AC,AD=CE,即可得出答案.
【答案与解析】
解:(1)平行四边形;
证明:∵AD=AB,AA′=AC,∴A′C与BD互相平分,
∴四边形A′BCD是平行四边形;
(2)∵DA由垂直于AB,逆时针旋转到点D、A、B在同一直线上,
∴旋转角为90度;
证明:∵∠D=∠B=90°,A,D,B在一条直线上,
∴CD∥BC′,∴四边形CDBC′是直角梯形;
故答案为:90,直角梯;
/
(3)四边形ADBC是等腰梯形;
证明:过点B作BM⊥AC,过点D作DN⊥AC,垂足分别为M,N,
∵有一张矩形纸片,将它沿对角线AC剪开,得到△ACD和△A′BC′.∴△ACD≌△A′BC′,
∴BM=ND,∴BD∥AC,
∵AD=BC,∴四边形ADBC是等腰梯形.
【总结升华】
此题主要考查了图形的剪拼与平行四边形的判定和等腰梯形的判定、直角梯形的判定方法等知识,熟练掌握判定定理是解题关键.
举一反三:
【图形的设计与操作及运动变换型问题 例1 】
【变式】△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点O为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1∶2,则线段AC的中点P变换后对应的点的坐标为______.
【答案】(/)或(/).
/5.如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位:cm2)与点P移动的时间(单位:s)的函数如图②所示,则点P从开始移动到停止移动一共用了 秒(结果保留根号).
/
【思路点拨】
根据图②判断出AB、BC的长度,过点B作BE⊥AD于点E,然后求出梯形ABCD的高BE,再根据t=2时△PAD的面积求出AD的长度,过点C作CF⊥AD于点F,然后求出DF的长度,利用勾股定理列式求出CD的长度,然后求出AB、BC、CD的和,再根据时间=路程÷速度,计算即可得解.
【答案】(4+2/).
【解析】
解:由图②可知,t在2到4秒时,△PAD的面积不发生变化,
∴在AB上运动的时间是2秒,在BC上运动的时间是4-2=2秒,
∵动点P的运动速度是1cm/s,
∴AB=2cm,BC=2cm,
过点B作BE⊥AD于点E,过点C作CF⊥AD于点F,
则四边形BCFE是矩形,
∴BE=CF,BC=EF=2cm,
∵∠A=60°,
∴BE=ABsin60°=2×/=/,
AE=ABcos60°=2×/=1,
∴/×AD×BE=3/,
即/×AD×/=3/,
解得AD=6cm,
∴DF=AD-AE-EF=6-1-2=3,
在Rt△CDF中,CD=/=/=2/,
所以,动点P运动的总路程为AB+BC+CD=2+2+2/=4+2/,
∵动点P的运动速度是1cm/s,
∴点P从开始移动到停止移动一共用了(4+2/)÷1=4+2/(秒).
故答案为:(4+2/).
/
【总结升华】
本题考查了动点问题的函数图象,根据图②的三角形的面积的变化情况判断出AB、BC的长度是解题的关键,在梯形的问题中,作过梯形的上底边的两个顶点的高线是常见的辅助线.
中考冲刺:动手操作与运动变换型问题—巩固练习(基础)
【巩固练习】
一、选择题
1. 如图,在Rt△ABC 中,∠C=90° ,AC=BC=6cm,点P从点A出发,沿AB方向以每秒/cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间t秒,若四边形QPCP为菱形,则t的值为( )
A. / B. 2 C. / D.3
2.如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A的方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t的值为( )
A. / B. 1 C. /或1 D. /或1或/
/ /
3. 如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为( )
/
/
二、填空题
4.如图,已知点A(0,2)、B(/,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连结AP,以AP为边在其左侧作等边△APQ ,连结PB、BA.若四边形ABPQ为梯形,则(1)当AB为梯形的底时,点P的横坐标是 ;(2)当AB为梯形的腰时,点P的横坐标是 .
/
5.如图,矩形纸片ABCD,AB=2,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好落在AC上,则AC的长是 .
/
6.如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是 .
三、解答题
7.如图所示是规格为8×8的正方形网格,请在所给网格中,按下列要求操作:
/
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点的坐标是________,△ABC的周长是________ (结果保留根号);
(3)画出△ABC以点C为旋转中心、旋转180°后的△A′B′C,连接AB′和A′B,试说出四边形/是何特殊四边形,并说明理由.
8. (1)观察与发现
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.
(2)实践与运用
将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.
/
9. 如图(1),已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角形板DEF绕D点按逆时针方向旋转.
(1)在图(1)中,DE交AB于M,DF交BC于N.
①证明:DM=ND;
②在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的;若不发生变化,求出其面积;
(2)继续旋转至如图(2)所示的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)继续旋转至如图(3)所示的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?若成立,请写出结论,不用证明.
/
10. 如图所示,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.
(1)试证明:无论点.P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的/?
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形?
/
【答案与解析】
一、选择题 1.【答案】B;
【解析】连接PP′交BC于点D,若四边形QPCP为菱形,则PP′⊥BC,CD=/CQ=/(6-t),
∴BD=6-/(6-t)=3+/t.在Rt△BPD中,PB=AB-AP=6/-/t,而PB=/BD,
∴6/-/t=/(3+/t),解得:t=2,故选B.
2.【答案】D;
【解析】∵AB是⊙O的直径,∴∠ACB=90°;Rt△ABC中,BC=2,∠ABC=60°; ∴AB=2BC=4cm.①当∠BFE=90°时;Rt△BEF中,∠ABC=60°,
则BE=2BF=2cm;故此时AE=AB-BE=2cm;∴E点运动的距离为:2cm或6cm,
故t=1s或3s;由于0≤t<3,故t=3s不合题意,舍去;所以当∠BFE=90°时,t=1s;②当∠BEF=90°时;同①可求得BE=0.5cm,此时AE=AB-BE=3.5cm;∴E点运动的距离为:3.5cm或4.5cm,故t=1.75s或2.25s;综上所述,当t的值为1、1.75或2.25s时,△BEF是直角三角形.故选D.
3.【答案】B.
【解析】在0≤x≤4时,y随x的增大而减小,在4≤x≤8时,y随x的增大而增大;且y与x的函数关系是二次函数,故选B.
二、填空题
4.【答案】(1)/;(2)0, /;
【解析】(1)由题意知,当AB为梯形的底时,AB∥PQ,即PQ⊥y轴,又△APQ为等边三角形,AC=2,由几何关系知,点P的横坐标是/.(2)当AB为梯形的腰时,当PB∥y轴时,满足题意,此时AQ=4,由几何关系得,点P的横坐标是/.
/ /
5.【答案】4;
【解析】由折叠可知∠BAE=∠CAE,因为AE=EC所以∠CAE=∠ACE,所以∠BAE=∠CAE=∠ACE,
三角的和为90°,所以∠ACE=30°,所以AC=2AB=4.
6.【答案】①④⑤.
【解析】由折叠知:∠ADG=∠GDO根据外角定理∠AGD=∠GDO+∠GOD而∠GOD=90°,
∠GDO = /∠ADO=22.5°得∠AGD=112.5°所以①正确.
由折叠知△AGD≌△FGD得S△AGD=S△FGD所以③错误.
∠AED=90°-22.5°=67.5°,∠AGE=45°+22.5°=67.5°故∠AED=∠AGE可得AE=AG,
易证AG=FG,AE=EF,从而得AG=FG=AE=EF.所以④正确.
BE=/EF,EF= FG=/OG,故BE=2OG所以⑤正确.
AE= FG=/OG,AD= AB=AE+ BE=(/+2)OG,在Rt△AED中tan∠AED=/=/,所以②错误.
三、解答题
7.【答案与解析】
(1)如图所示建立平面直角坐标系.
/
(2)如图画出点C,C(-1,1).△ABC的周长是/.
(3)如图画出△A′B′C,四边形ABA′B′是矩形.
理由:∵CA=CA′,CB=CB′,
∴四边形ABA′B′是平行四边形.
又∵CA=CB,
∴CA=CA′=CB=CB′.
∴AA′=BB′.
∴四边形ABA′B′是矩形.
8.【答案与解析】
解:(1)同意.
如图所示,设AD与EF交于点G.
/
由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.
又由折叠知,∠AGE=∠AGF=90°,
所以∠AEF=∠AFE,
所以AE=AF,即△AEF为等腰三角形.
(2)由折叠知,四边形ABFE是正方形∠AEB=45°,
所以∠BED=135°.
又由折叠知,∠BEG=∠DEG,
所以∠DEG=67.5°.
从而∠α=90°-67.5°=22.5°.
9.【答案与解析】
解:(1)①连接DB,利用△BMD≌△CND或△ADM∽△BDN即可证明DM=DN.
②由△BMD≌△CND知,/,
∴/.
即在直角三角板DEF旋转过程中,四边形DMBN的面积始终等于/,不发生变化.
/
(2)连接DB,由△BMD≌△CND可证明DM=DN,即DM=DN仍然成立.
(3)连接DB.由△BMD≌△CND,可证明DM=ND仍成立.
10.【答案与解析】
解:(1)证明:在正方形ABCD中,无论点P运动到AB上何处时,
都有AD=AB,∠DAQ=∠BAQ,AQ=AQ,∴△ADQ≌△ABQ.
(2)解:假设下图中△ADQ的面积恰好是正方形ABCD面积的/.
/
过点Q作QE⊥AD于E,QF⊥AB于F,则QE=QF,
/.
∴/.
由△DEQ∽△DAP得/,解得AP=2.
∴AP=2时,△ADQ的面积是正方形ABCD面积的/.
(3)若△ADQ是等腰三角形,则有DQ=QA或DA=DQ或AQ=AD.
①当点P运动到与点B重合时,由四边形ABCD是正方形知QD=QA,此时△ADQ是等腰三角形.
②当点P与点C重合时,点Q与点C也重合,此时DA=DQ,△ADQ是等腰三角形.
③如图所示,设点P在BC边上运动到CP=x时,有AD=AQ.
/
∵AD∥BC,∴∠ADQ=∠CPQ.
又∵∠AQD=∠CQP,∠ADQ=∠AQD,
∴∠CQP=∠CPQ.
∴CQ=CP=x.
∵AC=/,AQ=QD=4,
∴x=CQ=AC-AQ=/,
即当CP=/时,△ADQ是等腰三角形.
同课章节目录
