北师大版2020年中考总复习资料,补习复习资料:60数形结合问题(基础)含答案
文档属性
| 名称 | 北师大版2020年中考总复习资料,补习复习资料:60数形结合问题(基础)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 253.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-28 20:34:16 | ||
图片预览




文档简介
中考冲刺:数形结合问题—知识讲解(基础)
【中考展望】
1.用数形结合的思想解题可分两类:
(1)利用几何图形的直观性表示数的问题,它常借用数轴、函数图象等;
(2)运用数量关系来研究几何图形问题,常常要建立方程(组)或建立函数关系式等.
2. 热点内容:
在初中教材中,“数”的常见表现形式为: 实数、代数式、函数和不等式等,而“形”的常见表现形式为: 直线型、角、三角形、四边形、多边形、圆、抛物线、相似、勾股定理等.在直角坐标系下,一次函数图象对应一条直线,二次函数的图像对应着一条抛物线,这些都是初中数学的重要内容. 【方法点拨】
数形结合:就是通过数与形之间的对应和转化来解决数学问题,它包含“以形助数”和“以数解形”两个方面.利用它可使复杂问题简单化,抽象问题具体化,它兼有“数的严谨”与“形的直观”之长,是优化解题过程的重要途径之一,是一种基本的数学方法. 数形结合解题基本思路:“数”和“形”是数学中两个最基本的概念, 每一个几何图形中都蕴含着与它们的形状、大小、位置密切相关的数量关系;反之,数量关系又常常可以通过几何图形做出直观地反映和描述.数形结合的实质就是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合起来,在解决代数问题时,想到它的图形,从而启发思维,找到解题之路;或者在研究图形时,利用代数的知识,解决几何的问题.实现了抽象概念与具体图形的联系和转化,化难为易,化抽象为直观.
特别是二次函数,不仅是学生学习的难点之一,同时也使数形结合的思想方法在中学数学中得到最充分体现.在平面直角坐标系中,二次函数图象的开口方向、顶点坐标、对称轴以及与坐标轴的交点等都与其系数a,b,c密不可分.事实上,a的符号决定抛物线的开口方向,b与a 一起决定抛物线的对称轴的位置, c 决定了抛物线与y 轴的交点位置,与a、b 一起决定抛物线顶点坐标的纵坐标,抛物线图形的平移,只是顶点坐标发生变化,其实从代数的角度看是b、c 的有关变化.
在日常的数学学习中应注意养成数形相依的观念,有意识培养数形结合思想,形成数形统一意识,提高解题能力.“数缺形时少直观,形缺数时难入微.”总之,要把数形结合思想贯穿在数学学习中.数与形及其相互关系是数学研究的基本内容.
【典型例题】
类型一、利用数形结合探究数字的变化规律
/1. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第/个图形需要黑色棋子的个数是 .
/
【思路点拨】
首先计算几个特殊图形,发现:数出每边上的个数,乘以边数,但各个顶点的重复了一次,应再减
去.第1个图形是2×3-3,第2个图形是3×4-4,第3个图形是4×5-5,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n2+2n.
【答案与解析】
第1个图形是三角形,有3条边,每条边上有2个点,重复了3个点,需要黑色棋(2×3-3)个;
第2个图形是四边形,有4条边,每条边上有3个点,重复了4个点,需要黑色棋子(3×4-4)个; 第3个图形是五边形,有5条边,每条边上有4个点,重复了5个点,需要黑色棋子(4×5-5)个; 按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n(n+2). 故答案为n(n+2)=n2+2n.
【总结升华】这样的试题从最简单的图形入手.找出图形中黑点的个数与第n个图形之间的关系,找规
律需要列出算式,一律采用原题中的数据,不要用到计算出来的结果来找规律.
举一反三:
【变式】用棋子按下列方式摆图形,依照此规律,第n个图形比第(n-1)个图形多_____枚棋子.
/
【答案】解:设第n个图形的棋子数为. 第1个图形,S1=1; 第2个图形,S2=1+4; 第3个图形,S3=1+4+7;
第n个图形,Sn=1+4+…+3n-2; 第(n-1)个图形,Sn-1=1+4+…+[3(n-1)-2]; 则第n个图形比第(n-1)个图形多(3n-2)枚棋子.
类型二、 利用数形结合解决数与式的问题
/2.已知实数a、b、c在数轴上的位置如图所示,化简|a+b|-|c-b|的结果是 ( ).
/
A.a+c B.-a-2b+c C.a+2b-c D.-a-c
【思路点拨】
首先从数轴上a、b、c的位置关系可知:c<a<0;b>0且|b|>|a|,接着可得a+b>0,c-b<0,然后即可化简|a+b|-|c-b|可得结果. 具体步骤为:① a,b,c的具体位置,在原点左边的小于0,原点右边的大于0.②比较绝对值的大小.|a|<|c|<|b|.③化简原式中的每一部分,看看绝对值内部(二次根式中的被开方数的底数)的性质,若大于零,直接提出来,若小于零,则取原数的相反数.④进行化简计算,得出最后结果.
【答案与解析】
解:从数轴上a、b、c的位置关系可知:c<a<0;b>0且|b|>|a|,
故a+b>0,c-b<0,
即有|a+b|-|c-b|=a+b+c-b=a+c.
故选A.
【总结升华】
此题主要考查了利用数形结合的思想和方法来解决绝对值与数轴之间的关系,进而考察了非负数的
运用.数轴的特点:从原点向右为正数,向左为负数,及实数与数轴上的点的对应关系.非负数在初中的范围内,有三种形式:绝对值(|a|),完全平方式(a±b)2,二次根式(/.性质:非负数有最小值是0;几个非负数的和等于0,那么每一个非负数都等于0.
类型三、利用数形结合解决代数式的恒等变形问题
/3. 图①是一个边长为/的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
A. / B./
C./ D./
/
【思路点拨】
这是完全平方公式的几何背景,用几何图形来分析和理解完全平方公式的实质.是一个很典型的“数形结合”的例子,用图形的变换来帮助理解代数学中的枯燥无味的数学公式.根据图示可知,阴影部分的面积是边长为(m+n)的正方形的面积减去中间白色的小正方形的面积(m2+n2),即为对角线分别是2m,2n的菱形的面积.据此即可解答.
【答案】B.
【解析】(m+n)2-(m2+n2)=2mn. 故选B.
【总结升华】
本题是利用几何图形的面积来验证(m+n)2-(m2+n2)=2mn,解题关键是利用图形的面积之间的相等关系列等式.
举一反三:
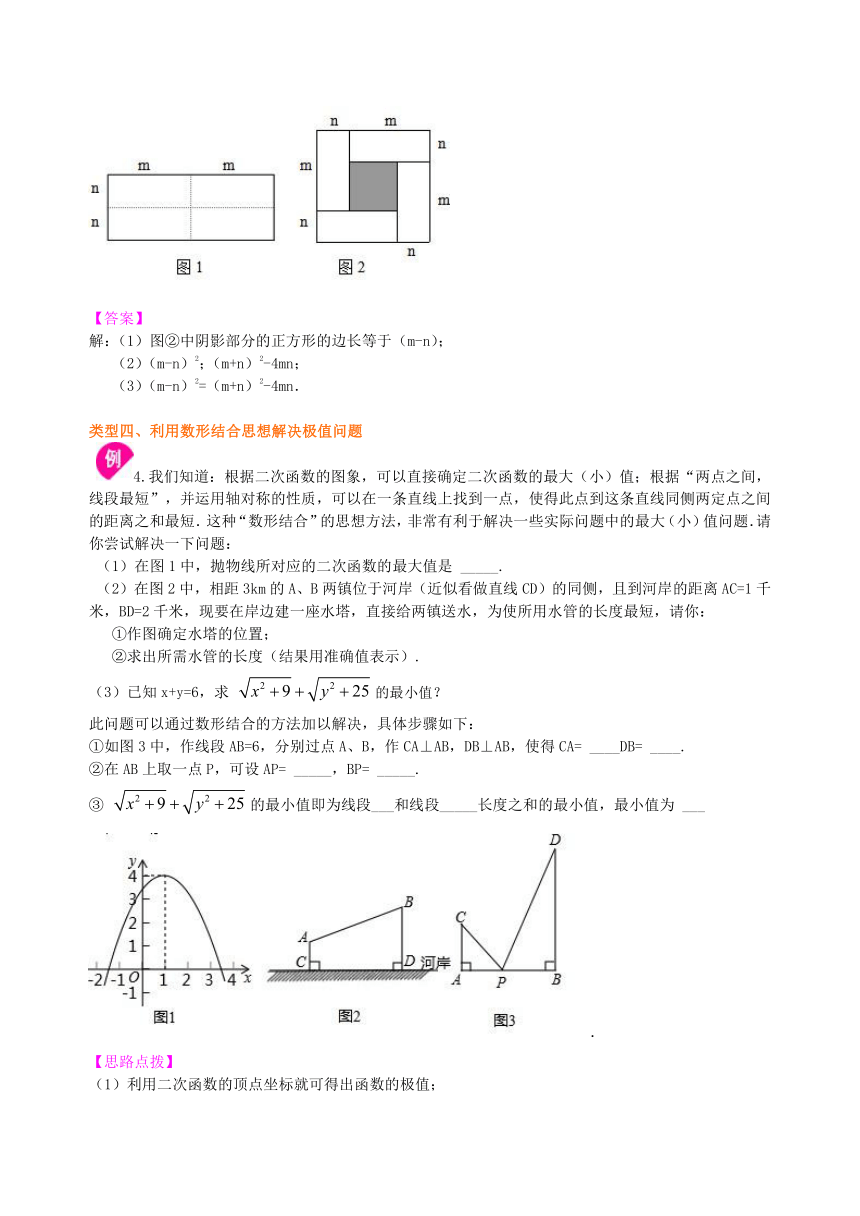
【变式】如图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个空心正方形. (1)你认为图2中的阴影部分的正方形的边长是多少? (2)请用两种不同的方法求出图2中阴影部分的面积;
(3)观察图2,你能写出下列三个代数式:(m+n)2、(m-n)2、mn之间的关系吗?
/
【答案】
解:(1)图②中阴影部分的正方形的边长等于(m-n); (2)(m-n)2;(m+n)2-4mn; (3)(m-n)2=(m+n)2-4mn.
类型四、利用数形结合思想解决极值问题
/4.我们知道:根据二次函数的图象,可以直接确定二次函数的最大(小)值;根据“两点之间,线段最短”,并运用轴对称的性质,可以在一条直线上找到一点,使得此点到这条直线同侧两定点之间的距离之和最短.这种“数形结合”的思想方法,非常有利于解决一些实际问题中的最大(小)值问题.请你尝试解决一下问题: (1)在图1中,抛物线所对应的二次函数的最大值是 _____.
(2)在图2中,相距3km的A、B两镇位于河岸(近似看做直线CD)的同侧,且到河岸的距离AC=1千米,BD=2千米,现要在岸边建一座水塔,直接给两镇送水,为使所用水管的长度最短,请你: ①作图确定水塔的位置; ②求出所需水管的长度(结果用准确值表示). (3)已知x+y=6,求 /的最小值?
此问题可以通过数形结合的方法加以解决,具体步骤如下: ①如图3中,作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA= ____DB= ____. ②在AB上取一点P,可设AP= _____,BP= _____. ③ /的最小值即为线段___和线段_____长度之和的最小值,最小值为 ___
/.
【思路点拨】
(1)利用二次函数的顶点坐标就可得出函数的极值; (2)①延长AC到点E,使CE=AC,连接BE,交直线CD于点P,则点P即为所求; ②过点A作AF⊥BD,垂足为F,过点E作EG⊥BD,交BD的延长线于点G,则有四边形ACDF、CEGD都是矩形,进而利用勾股定理求出即可; (3)①作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA=3,BD=5, ②在AB上取一点P,可设AP=x,BP=y; ③/的最小值即为线段 PC和线段 PD长度之和的最小值,最小值利用勾股定理求出即可.
【答案与解析】
解:(1)抛物线所对应的二次函数的最大值是4; /
(2)①如图所示,点P即为所求. (作法:延长AC到点E,使CE=AC,连接BE,交直线CD于点P,则 点P即为所求. 说明:不必写作法和证明,但要保留作图痕迹;不连接PA不扣分;(延长BD,同样的方法也可以得到P点的位置.) ②过点A作AF⊥BD,垂足为F,过点E作EG⊥BD,交BD的延长线于点G,则有四边形ACDF、CEGD
都是矩形. ∴FD=AC=CE=DG=1,EG=CD=AF. ∵AB=3,BD=2, ∴BF=BD-FD=1,BG=BD+DG=3, ∴在Rt△ABF中,AF2=AB2-BF2=8, ∴AF=2/ EG=2/.
∴在Rt△BEG中,BE2=EG2+BG2=17,
∴BE=/(cm). ∴PA+PB的最小值为/cm. 即所用水管的最短长度为/cm.
(3)图3所示,①作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA=3,BD=5, ②在AB上取一点P,可设AP=x,BP=y, ③/的最小值即为线段 PC和线段 PD长度之和的最小值,
/
∴作C点关于线段AB的对称点C′,连接C′D,过C′点作C′E⊥DB,交BD延长线于点E, ∵AC=BE=3,DB=5,AB=C′E=6, ∴DE=8, /.
∴最小值为10.
故答案为:①4; ②x,y; ③PC,PD,10.
【总结升华】
此题主要考查了函数最值问题与利用轴对称求最短路线问题,结合已知画出图象利用数形结合以及勾股定理是解题关键.
作图题不要求写出作法,但必须保留痕迹.最后点题,即“xx即为所求”.
类型五、利用数形结合思想,解决函数问题
/5.如图,二次函数y=ax2+bx+c的图象开口向上,图象过点(-1,2)和(1,0),且与y轴相交与负半轴.以下结论(1)a>0;(2)b>0;(3)c>0;(4)a+b+c=0;(5)abc<0;(6)2a+b>0;(7)a+c=1;(8)a>1中,正确结论的序号是___________.
/
【思路点拨】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【答案与解析】
解:(1)①由抛物线的开口方向向上,可推出a>0,正确; ②因为对称轴在y轴右侧,对称轴为x=/>0,又因为a>0,∴b<0,错误; ③由抛物线与y轴的交点在y轴的负半轴上,∴c<0,错误; ④由图象可知:当x=1时y=0,∴a+b+c=0,正确;
⑤∵a>0,b<0,c<0,∴abc>0,错误; ⑥由图象可知:对称轴x=/>0且对称轴x=/<1,∴2a+b>0,正确; ⑦由图象可知:当x=-1时y=2,∴a-b+c=2, ---①
当x=1时y=0,∴a+b+c=0, ---②
①+②,得
2a+2c=2,解得 a+c=1,正确; ⑧∵a+c=1,移项得a=1-c,又∵c<0,∴a>1,正确. 故正确结论的序号是①④⑥⑦⑧.
【总结升华】
考查二次函数的解析式、图象,及综合应用相关知识分析问题、解决问题的能力.
二次函数y=ax2+bx+c图象与系数之间的关系: (1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0. (2)b由对称轴和a的符号确定:由对称轴公式x=/判断符号.存在着“左同右异”,即a,b同号.对称轴在y轴的左边,a,b异号,对称轴在y轴的右边. (3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0. (4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.
(5)当x=±1时,ax2+bx+c就变成了a±b+c了.这道题的第7小题:当x=1时,a+b+c=0……①
当x=-1时,a-b+c=2……②,①+②得,2a+2c=2,即a+c=1.
举一反三:
【变式】已知二次函数y=ax2+bx+c的图象如图所示,x=/是该抛物线的对称轴.根据图中所提供的信息,请你写出有关a,b,c的四条结论,并简单说明理由.
【答案】解:①∵开口方向向上,∴a>0, ②∵与y轴的交点为在y轴的正半轴上,∴c>0, ③∵对称轴为x=/>0,∴a、b异号,即b<0, ④∵抛物线与x轴有两个交点,∴b2-4ac>0, ⑤当x=1时,y=a+b+c<0, ⑥当x=-1时,y=a-b+c>0. 结论有:a>0,b<0,c<0,a+b+c<0,a-b+c>0等.
/
中考冲刺:数形结合问题—巩固练习(基础)
【巩固练习】
选择题
1.当k<0时,反比例函数/和一次函数y=kx-k的图象大致是( )
/
2.从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙)。那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A 、/ B、/
C、/ D、/
/
二、 填空题
3. 实数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的序号为____________.
①b+c>0 ②a+b>a+c ③ac<bc ④ab>ac
/
4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: (1)4a+2b+c>0; (2)方程ax2+bx+c=0两根之和小于零; (3)y随x的增大而增大; (4)4a-2b+c<0; (5)b2-4ac<0; (6)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数有______个.
/
三、解答题
5.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么2个小时时血液中含药最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当成人按规定剂量服药后.
(1)分别求出x≤2和x≥2时y与x的函数解析式;
(2)如果每毫升血液中含量为4微克或4微克以上时,在治疗疾病时是有效的,那么这个有效时间有
多长?
/
6.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. / (1)你认为图2中的阴影部分的正方形的边长等于 _____; (2)请用两种不同的方法求图2中阴影部分的面积.① ______②_______; (3)观察图2你能写出下列三个代数式之间的等量关系吗?
(4)运用你所得到的公式,计算若mn=-2,m-n=4,求(m+n)2的值. (5)用完全平方公式和非负数的性质求代数式x2+2x+y2-4y+7的最小值.
7.为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示: (1)分别求出通话费y1,y2与通话时间x之间的函数关系式; (2)请帮用户计算,在一个月内使用哪一种卡便宜.
/
8.如图,一次函数图象与x轴相交于点B,与反比例函数图象相交于点A(1,-6);△AOB的面积为6.求一次函数和反比例函数的解析式.
/
9.请同学们仔细阅读如图所示的计算机程序框架图,回答下列问题: (1)如果输入值为2,那么输出值是多少? (2)若要使输入的x的值只经过一次运行就能输出结果,求x的取值范围; (3)若要使开始输入的x的值经过两次运行才能输出结果,那么x的取值范围又是多少?
/
10.观察如图所包含规律(图中三角形均是直角三角形,且一条直角边始终为1,四边形均为正方形.S1,S2,S3,…Sn依次表示正方形的面积,每个正方形边长与它左边相邻的直角三角形斜边相等),再回答下列问题. (1)填表:
直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
…
(2)当s1+s2+s3+s4+…+sn=465时,求n.
/
11.某报社为了了解读者对该报社一种报纸四个版面的认可情况,对读者做了一次问卷凋查,要求读者选出自己最喜欢的一个版面,并将调查结果绘制成如下的统计图,请你根据图中提供的信息解答下列问题. (1)在这次活动中一共调查了多少读者? (2)在扇形统计图中,计算第一版所在扇形的圆心角度数; (3)请你求出喜欢第四版的人数,并将条形统计图补充完整.
/
【答案与解析】
一、选择题
1.【答案】B;
2.【答案】D;
二、 填空题
3.【答案】②③④;
4.【答案】1;
三、 解答题
5.【答案与解析】
解:(1)当x≤2时,设y=kx, 把(2,6)代入上式,得k=3, ∴x≤2时,y=3x; 当x≥2时,设y=kx+b, 把(2,6),(10,3)代入上式,得
k=/,b=/ ∴x≥2时,y=/x+/
(2)把y=4代入y=3x,得x1=/ 把y=4代入y=/x+/ 得x2=/
则x2-x1=6(小时).
答:这个有效时间为6小时.
6.【答案与解析】
解:(1)由图可知,阴影部分小正方形的边长为:m-n;
(2)根据正方形的面积公式,阴影部分的面积为(m-n)2,
还可以表示为(m+n)2-4mn;
(3)根据阴影部分的面积相等,(m-n)2=(m+n)2-4mn; (4)∵mn=-2,m-n=4, ∴(m+n)2=(m-n)2+4mn=42+4×(-2)=16-8=8;
(5)x2+2x+y2-4y+7, =x2+2x+1+y2-4y+4+2, =(x+1)2+(y-2)2+2, ∵(x+1)2≥0,(y-2)2≥0, ∴(x+1)2+(y-2)2≥2, ∴当x=-1,y=2时,代数式x2+2x+y2-4y+7的最小值是2. 故答案为:(1)m-n;(2)(m-n)2,(m+n)2-4mn;(3)(m-n)2=(m+n)2-4mn.(4) 8 (5) 最
小值是2.
7.【答案与解析】
解:(1)设y1=kx+b,将(0,29),(30,35)代入,
解得k=/,b=29,∴y1=/x+29,
又24×60×30=43200(min)(属于隐含条件)
∴y1=/x+29 (0≤x≤43200),
同样求得y2=/x (0≤x≤43200);
(2)当y1=y2时,
/x+29=/x,
x=/;
当y1<y2时,
/x+29</x, x>/.
所以,当通话时间等于/min时,两种卡的收费一致, 当通话时间小于/min时,“如意卡便宜”, 当通话时间大于/min时,“便民卡”便宜.
8.【答案与解析】
解:设反比例函数解析式为:y=/(k≠0), ∵点A(1,-6)在反比例函数图象上 ∴k=1×(-6)=-6, 即反比例函数关系式为y=-/, ∵△AOB的面积为6. ∴/×OB×6=6, ∴OB=2, ∴B(-2,0), 设一次函数解析式为:y=kx+b, ∵图象经过A(1,-6),B(-2,0), ∴/
解得:/ ∴一次函数解析式为:y=-2x-4.
9.【答案与解析】
解:(1)依据题中的计算程序列出算式:3×2+1, ∵3×2+1=7,7<9, ∴应该按照计算程序继续计算,3×7+1=22>9, ∴如果输入值为2,那么输出值是22.
(2)依题意,有3x+1>9, 解得x>/;
(3)依题意,有/
解得/<x≤/.
10.【答案与解析】
解:(1)/,
/,
直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
/
/
2
…
(2)S1=(/)2=2, S2=(/)2=3, S3=22=4, S4=(/)2=5,…….. Sn=(/)2=n+1; 由s1+s2+s3+s4+…+sn=465可得: 1+2+3+4+5+…+n=465,
/(1+n) ×n=465
解得:n=-31(不合题意舍去)或n=30, 故:n=30.
11.【答案与解析】
解:(1)这次活动中一共调查了500÷10%=5000(人); (2)第一版所在扇形的圆心角度数=360°×(1-20%-40%-10%)=108°; (3)喜欢第四版的人数是: 5000×20%=1000(人),如下图所示:
/ /
中考冲刺:数形结合问题—知识讲解(基础)
【中考展望】
1.用数形结合的思想解题可分两类:
(1)利用几何图形的直观性表示数的问题,它常借用数轴、函数图象等;
(2)运用数量关系来研究几何图形问题,常常要建立方程(组)或建立函数关系式等.
2. 热点内容:
在初中教材中,“数”的常见表现形式为: 实数、代数式、函数和不等式等,而“形”的常见表现形式为: 直线型、角、三角形、四边形、多边形、圆、抛物线、相似、勾股定理等.在直角坐标系下,一次函数图象对应一条直线,二次函数的图像对应着一条抛物线,这些都是初中数学的重要内容. 【方法点拨】
数形结合:就是通过数与形之间的对应和转化来解决数学问题,它包含“以形助数”和“以数解形”两个方面.利用它可使复杂问题简单化,抽象问题具体化,它兼有“数的严谨”与“形的直观”之长,是优化解题过程的重要途径之一,是一种基本的数学方法. 数形结合解题基本思路:“数”和“形”是数学中两个最基本的概念, 每一个几何图形中都蕴含着与它们的形状、大小、位置密切相关的数量关系;反之,数量关系又常常可以通过几何图形做出直观地反映和描述.数形结合的实质就是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合起来,在解决代数问题时,想到它的图形,从而启发思维,找到解题之路;或者在研究图形时,利用代数的知识,解决几何的问题.实现了抽象概念与具体图形的联系和转化,化难为易,化抽象为直观.
特别是二次函数,不仅是学生学习的难点之一,同时也使数形结合的思想方法在中学数学中得到最充分体现.在平面直角坐标系中,二次函数图象的开口方向、顶点坐标、对称轴以及与坐标轴的交点等都与其系数a,b,c密不可分.事实上,a的符号决定抛物线的开口方向,b与a 一起决定抛物线的对称轴的位置, c 决定了抛物线与y 轴的交点位置,与a、b 一起决定抛物线顶点坐标的纵坐标,抛物线图形的平移,只是顶点坐标发生变化,其实从代数的角度看是b、c 的有关变化.
在日常的数学学习中应注意养成数形相依的观念,有意识培养数形结合思想,形成数形统一意识,提高解题能力.“数缺形时少直观,形缺数时难入微.”总之,要把数形结合思想贯穿在数学学习中.数与形及其相互关系是数学研究的基本内容.
【典型例题】
类型一、利用数形结合探究数字的变化规律
/1. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第/个图形需要黑色棋子的个数是 .
/
【思路点拨】
首先计算几个特殊图形,发现:数出每边上的个数,乘以边数,但各个顶点的重复了一次,应再减
去.第1个图形是2×3-3,第2个图形是3×4-4,第3个图形是4×5-5,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n2+2n.
【答案与解析】
第1个图形是三角形,有3条边,每条边上有2个点,重复了3个点,需要黑色棋(2×3-3)个;
第2个图形是四边形,有4条边,每条边上有3个点,重复了4个点,需要黑色棋子(3×4-4)个; 第3个图形是五边形,有5条边,每条边上有4个点,重复了5个点,需要黑色棋子(4×5-5)个; 按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n(n+2). 故答案为n(n+2)=n2+2n.
【总结升华】这样的试题从最简单的图形入手.找出图形中黑点的个数与第n个图形之间的关系,找规
律需要列出算式,一律采用原题中的数据,不要用到计算出来的结果来找规律.
举一反三:
【变式】用棋子按下列方式摆图形,依照此规律,第n个图形比第(n-1)个图形多_____枚棋子.
/
【答案】解:设第n个图形的棋子数为. 第1个图形,S1=1; 第2个图形,S2=1+4; 第3个图形,S3=1+4+7;
第n个图形,Sn=1+4+…+3n-2; 第(n-1)个图形,Sn-1=1+4+…+[3(n-1)-2]; 则第n个图形比第(n-1)个图形多(3n-2)枚棋子.
类型二、 利用数形结合解决数与式的问题
/2.已知实数a、b、c在数轴上的位置如图所示,化简|a+b|-|c-b|的结果是 ( ).
/
A.a+c B.-a-2b+c C.a+2b-c D.-a-c
【思路点拨】
首先从数轴上a、b、c的位置关系可知:c<a<0;b>0且|b|>|a|,接着可得a+b>0,c-b<0,然后即可化简|a+b|-|c-b|可得结果. 具体步骤为:① a,b,c的具体位置,在原点左边的小于0,原点右边的大于0.②比较绝对值的大小.|a|<|c|<|b|.③化简原式中的每一部分,看看绝对值内部(二次根式中的被开方数的底数)的性质,若大于零,直接提出来,若小于零,则取原数的相反数.④进行化简计算,得出最后结果.
【答案与解析】
解:从数轴上a、b、c的位置关系可知:c<a<0;b>0且|b|>|a|,
故a+b>0,c-b<0,
即有|a+b|-|c-b|=a+b+c-b=a+c.
故选A.
【总结升华】
此题主要考查了利用数形结合的思想和方法来解决绝对值与数轴之间的关系,进而考察了非负数的
运用.数轴的特点:从原点向右为正数,向左为负数,及实数与数轴上的点的对应关系.非负数在初中的范围内,有三种形式:绝对值(|a|),完全平方式(a±b)2,二次根式(/.性质:非负数有最小值是0;几个非负数的和等于0,那么每一个非负数都等于0.
类型三、利用数形结合解决代数式的恒等变形问题
/3. 图①是一个边长为/的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
A. / B./
C./ D./
/
【思路点拨】
这是完全平方公式的几何背景,用几何图形来分析和理解完全平方公式的实质.是一个很典型的“数形结合”的例子,用图形的变换来帮助理解代数学中的枯燥无味的数学公式.根据图示可知,阴影部分的面积是边长为(m+n)的正方形的面积减去中间白色的小正方形的面积(m2+n2),即为对角线分别是2m,2n的菱形的面积.据此即可解答.
【答案】B.
【解析】(m+n)2-(m2+n2)=2mn. 故选B.
【总结升华】
本题是利用几何图形的面积来验证(m+n)2-(m2+n2)=2mn,解题关键是利用图形的面积之间的相等关系列等式.
举一反三:
【变式】如图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个空心正方形. (1)你认为图2中的阴影部分的正方形的边长是多少? (2)请用两种不同的方法求出图2中阴影部分的面积;
(3)观察图2,你能写出下列三个代数式:(m+n)2、(m-n)2、mn之间的关系吗?
/
【答案】
解:(1)图②中阴影部分的正方形的边长等于(m-n); (2)(m-n)2;(m+n)2-4mn; (3)(m-n)2=(m+n)2-4mn.
类型四、利用数形结合思想解决极值问题
/4.我们知道:根据二次函数的图象,可以直接确定二次函数的最大(小)值;根据“两点之间,线段最短”,并运用轴对称的性质,可以在一条直线上找到一点,使得此点到这条直线同侧两定点之间的距离之和最短.这种“数形结合”的思想方法,非常有利于解决一些实际问题中的最大(小)值问题.请你尝试解决一下问题: (1)在图1中,抛物线所对应的二次函数的最大值是 _____.
(2)在图2中,相距3km的A、B两镇位于河岸(近似看做直线CD)的同侧,且到河岸的距离AC=1千米,BD=2千米,现要在岸边建一座水塔,直接给两镇送水,为使所用水管的长度最短,请你: ①作图确定水塔的位置; ②求出所需水管的长度(结果用准确值表示). (3)已知x+y=6,求 /的最小值?
此问题可以通过数形结合的方法加以解决,具体步骤如下: ①如图3中,作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA= ____DB= ____. ②在AB上取一点P,可设AP= _____,BP= _____. ③ /的最小值即为线段___和线段_____长度之和的最小值,最小值为 ___
/.
【思路点拨】
(1)利用二次函数的顶点坐标就可得出函数的极值; (2)①延长AC到点E,使CE=AC,连接BE,交直线CD于点P,则点P即为所求; ②过点A作AF⊥BD,垂足为F,过点E作EG⊥BD,交BD的延长线于点G,则有四边形ACDF、CEGD都是矩形,进而利用勾股定理求出即可; (3)①作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA=3,BD=5, ②在AB上取一点P,可设AP=x,BP=y; ③/的最小值即为线段 PC和线段 PD长度之和的最小值,最小值利用勾股定理求出即可.
【答案与解析】
解:(1)抛物线所对应的二次函数的最大值是4; /
(2)①如图所示,点P即为所求. (作法:延长AC到点E,使CE=AC,连接BE,交直线CD于点P,则 点P即为所求. 说明:不必写作法和证明,但要保留作图痕迹;不连接PA不扣分;(延长BD,同样的方法也可以得到P点的位置.) ②过点A作AF⊥BD,垂足为F,过点E作EG⊥BD,交BD的延长线于点G,则有四边形ACDF、CEGD
都是矩形. ∴FD=AC=CE=DG=1,EG=CD=AF. ∵AB=3,BD=2, ∴BF=BD-FD=1,BG=BD+DG=3, ∴在Rt△ABF中,AF2=AB2-BF2=8, ∴AF=2/ EG=2/.
∴在Rt△BEG中,BE2=EG2+BG2=17,
∴BE=/(cm). ∴PA+PB的最小值为/cm. 即所用水管的最短长度为/cm.
(3)图3所示,①作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA=3,BD=5, ②在AB上取一点P,可设AP=x,BP=y, ③/的最小值即为线段 PC和线段 PD长度之和的最小值,
/
∴作C点关于线段AB的对称点C′,连接C′D,过C′点作C′E⊥DB,交BD延长线于点E, ∵AC=BE=3,DB=5,AB=C′E=6, ∴DE=8, /.
∴最小值为10.
故答案为:①4; ②x,y; ③PC,PD,10.
【总结升华】
此题主要考查了函数最值问题与利用轴对称求最短路线问题,结合已知画出图象利用数形结合以及勾股定理是解题关键.
作图题不要求写出作法,但必须保留痕迹.最后点题,即“xx即为所求”.
类型五、利用数形结合思想,解决函数问题
/5.如图,二次函数y=ax2+bx+c的图象开口向上,图象过点(-1,2)和(1,0),且与y轴相交与负半轴.以下结论(1)a>0;(2)b>0;(3)c>0;(4)a+b+c=0;(5)abc<0;(6)2a+b>0;(7)a+c=1;(8)a>1中,正确结论的序号是___________.
/
【思路点拨】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【答案与解析】
解:(1)①由抛物线的开口方向向上,可推出a>0,正确; ②因为对称轴在y轴右侧,对称轴为x=/>0,又因为a>0,∴b<0,错误; ③由抛物线与y轴的交点在y轴的负半轴上,∴c<0,错误; ④由图象可知:当x=1时y=0,∴a+b+c=0,正确;
⑤∵a>0,b<0,c<0,∴abc>0,错误; ⑥由图象可知:对称轴x=/>0且对称轴x=/<1,∴2a+b>0,正确; ⑦由图象可知:当x=-1时y=2,∴a-b+c=2, ---①
当x=1时y=0,∴a+b+c=0, ---②
①+②,得
2a+2c=2,解得 a+c=1,正确; ⑧∵a+c=1,移项得a=1-c,又∵c<0,∴a>1,正确. 故正确结论的序号是①④⑥⑦⑧.
【总结升华】
考查二次函数的解析式、图象,及综合应用相关知识分析问题、解决问题的能力.
二次函数y=ax2+bx+c图象与系数之间的关系: (1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0. (2)b由对称轴和a的符号确定:由对称轴公式x=/判断符号.存在着“左同右异”,即a,b同号.对称轴在y轴的左边,a,b异号,对称轴在y轴的右边. (3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0. (4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.
(5)当x=±1时,ax2+bx+c就变成了a±b+c了.这道题的第7小题:当x=1时,a+b+c=0……①
当x=-1时,a-b+c=2……②,①+②得,2a+2c=2,即a+c=1.
举一反三:
【变式】已知二次函数y=ax2+bx+c的图象如图所示,x=/是该抛物线的对称轴.根据图中所提供的信息,请你写出有关a,b,c的四条结论,并简单说明理由.
【答案】解:①∵开口方向向上,∴a>0, ②∵与y轴的交点为在y轴的正半轴上,∴c>0, ③∵对称轴为x=/>0,∴a、b异号,即b<0, ④∵抛物线与x轴有两个交点,∴b2-4ac>0, ⑤当x=1时,y=a+b+c<0, ⑥当x=-1时,y=a-b+c>0. 结论有:a>0,b<0,c<0,a+b+c<0,a-b+c>0等.
/
中考冲刺:数形结合问题—巩固练习(基础)
【巩固练习】
选择题
1.当k<0时,反比例函数/和一次函数y=kx-k的图象大致是( )
/
2.从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙)。那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A 、/ B、/
C、/ D、/
/
二、 填空题
3. 实数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的序号为____________.
①b+c>0 ②a+b>a+c ③ac<bc ④ab>ac
/
4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: (1)4a+2b+c>0; (2)方程ax2+bx+c=0两根之和小于零; (3)y随x的增大而增大; (4)4a-2b+c<0; (5)b2-4ac<0; (6)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数有______个.
/
三、解答题
5.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么2个小时时血液中含药最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当成人按规定剂量服药后.
(1)分别求出x≤2和x≥2时y与x的函数解析式;
(2)如果每毫升血液中含量为4微克或4微克以上时,在治疗疾病时是有效的,那么这个有效时间有
多长?
/
6.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. / (1)你认为图2中的阴影部分的正方形的边长等于 _____; (2)请用两种不同的方法求图2中阴影部分的面积.① ______②_______; (3)观察图2你能写出下列三个代数式之间的等量关系吗?
(4)运用你所得到的公式,计算若mn=-2,m-n=4,求(m+n)2的值. (5)用完全平方公式和非负数的性质求代数式x2+2x+y2-4y+7的最小值.
7.为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示: (1)分别求出通话费y1,y2与通话时间x之间的函数关系式; (2)请帮用户计算,在一个月内使用哪一种卡便宜.
/
8.如图,一次函数图象与x轴相交于点B,与反比例函数图象相交于点A(1,-6);△AOB的面积为6.求一次函数和反比例函数的解析式.
/
9.请同学们仔细阅读如图所示的计算机程序框架图,回答下列问题: (1)如果输入值为2,那么输出值是多少? (2)若要使输入的x的值只经过一次运行就能输出结果,求x的取值范围; (3)若要使开始输入的x的值经过两次运行才能输出结果,那么x的取值范围又是多少?
/
10.观察如图所包含规律(图中三角形均是直角三角形,且一条直角边始终为1,四边形均为正方形.S1,S2,S3,…Sn依次表示正方形的面积,每个正方形边长与它左边相邻的直角三角形斜边相等),再回答下列问题. (1)填表:
直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
…
(2)当s1+s2+s3+s4+…+sn=465时,求n.
/
11.某报社为了了解读者对该报社一种报纸四个版面的认可情况,对读者做了一次问卷凋查,要求读者选出自己最喜欢的一个版面,并将调查结果绘制成如下的统计图,请你根据图中提供的信息解答下列问题. (1)在这次活动中一共调查了多少读者? (2)在扇形统计图中,计算第一版所在扇形的圆心角度数; (3)请你求出喜欢第四版的人数,并将条形统计图补充完整.
/
【答案与解析】
一、选择题
1.【答案】B;
2.【答案】D;
二、 填空题
3.【答案】②③④;
4.【答案】1;
三、 解答题
5.【答案与解析】
解:(1)当x≤2时,设y=kx, 把(2,6)代入上式,得k=3, ∴x≤2时,y=3x; 当x≥2时,设y=kx+b, 把(2,6),(10,3)代入上式,得
k=/,b=/ ∴x≥2时,y=/x+/
(2)把y=4代入y=3x,得x1=/ 把y=4代入y=/x+/ 得x2=/
则x2-x1=6(小时).
答:这个有效时间为6小时.
6.【答案与解析】
解:(1)由图可知,阴影部分小正方形的边长为:m-n;
(2)根据正方形的面积公式,阴影部分的面积为(m-n)2,
还可以表示为(m+n)2-4mn;
(3)根据阴影部分的面积相等,(m-n)2=(m+n)2-4mn; (4)∵mn=-2,m-n=4, ∴(m+n)2=(m-n)2+4mn=42+4×(-2)=16-8=8;
(5)x2+2x+y2-4y+7, =x2+2x+1+y2-4y+4+2, =(x+1)2+(y-2)2+2, ∵(x+1)2≥0,(y-2)2≥0, ∴(x+1)2+(y-2)2≥2, ∴当x=-1,y=2时,代数式x2+2x+y2-4y+7的最小值是2. 故答案为:(1)m-n;(2)(m-n)2,(m+n)2-4mn;(3)(m-n)2=(m+n)2-4mn.(4) 8 (5) 最
小值是2.
7.【答案与解析】
解:(1)设y1=kx+b,将(0,29),(30,35)代入,
解得k=/,b=29,∴y1=/x+29,
又24×60×30=43200(min)(属于隐含条件)
∴y1=/x+29 (0≤x≤43200),
同样求得y2=/x (0≤x≤43200);
(2)当y1=y2时,
/x+29=/x,
x=/;
当y1<y2时,
/x+29</x, x>/.
所以,当通话时间等于/min时,两种卡的收费一致, 当通话时间小于/min时,“如意卡便宜”, 当通话时间大于/min时,“便民卡”便宜.
8.【答案与解析】
解:设反比例函数解析式为:y=/(k≠0), ∵点A(1,-6)在反比例函数图象上 ∴k=1×(-6)=-6, 即反比例函数关系式为y=-/, ∵△AOB的面积为6. ∴/×OB×6=6, ∴OB=2, ∴B(-2,0), 设一次函数解析式为:y=kx+b, ∵图象经过A(1,-6),B(-2,0), ∴/
解得:/ ∴一次函数解析式为:y=-2x-4.
9.【答案与解析】
解:(1)依据题中的计算程序列出算式:3×2+1, ∵3×2+1=7,7<9, ∴应该按照计算程序继续计算,3×7+1=22>9, ∴如果输入值为2,那么输出值是22.
(2)依题意,有3x+1>9, 解得x>/;
(3)依题意,有/
解得/<x≤/.
10.【答案与解析】
解:(1)/,
/,
直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
/
/
2
…
(2)S1=(/)2=2, S2=(/)2=3, S3=22=4, S4=(/)2=5,…….. Sn=(/)2=n+1; 由s1+s2+s3+s4+…+sn=465可得: 1+2+3+4+5+…+n=465,
/(1+n) ×n=465
解得:n=-31(不合题意舍去)或n=30, 故:n=30.
11.【答案与解析】
解:(1)这次活动中一共调查了500÷10%=5000(人); (2)第一版所在扇形的圆心角度数=360°×(1-20%-40%-10%)=108°; (3)喜欢第四版的人数是: 5000×20%=1000(人),如下图所示:
/ /
【中考展望】
1.用数形结合的思想解题可分两类:
(1)利用几何图形的直观性表示数的问题,它常借用数轴、函数图象等;
(2)运用数量关系来研究几何图形问题,常常要建立方程(组)或建立函数关系式等.
2. 热点内容:
在初中教材中,“数”的常见表现形式为: 实数、代数式、函数和不等式等,而“形”的常见表现形式为: 直线型、角、三角形、四边形、多边形、圆、抛物线、相似、勾股定理等.在直角坐标系下,一次函数图象对应一条直线,二次函数的图像对应着一条抛物线,这些都是初中数学的重要内容. 【方法点拨】
数形结合:就是通过数与形之间的对应和转化来解决数学问题,它包含“以形助数”和“以数解形”两个方面.利用它可使复杂问题简单化,抽象问题具体化,它兼有“数的严谨”与“形的直观”之长,是优化解题过程的重要途径之一,是一种基本的数学方法. 数形结合解题基本思路:“数”和“形”是数学中两个最基本的概念, 每一个几何图形中都蕴含着与它们的形状、大小、位置密切相关的数量关系;反之,数量关系又常常可以通过几何图形做出直观地反映和描述.数形结合的实质就是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合起来,在解决代数问题时,想到它的图形,从而启发思维,找到解题之路;或者在研究图形时,利用代数的知识,解决几何的问题.实现了抽象概念与具体图形的联系和转化,化难为易,化抽象为直观.
特别是二次函数,不仅是学生学习的难点之一,同时也使数形结合的思想方法在中学数学中得到最充分体现.在平面直角坐标系中,二次函数图象的开口方向、顶点坐标、对称轴以及与坐标轴的交点等都与其系数a,b,c密不可分.事实上,a的符号决定抛物线的开口方向,b与a 一起决定抛物线的对称轴的位置, c 决定了抛物线与y 轴的交点位置,与a、b 一起决定抛物线顶点坐标的纵坐标,抛物线图形的平移,只是顶点坐标发生变化,其实从代数的角度看是b、c 的有关变化.
在日常的数学学习中应注意养成数形相依的观念,有意识培养数形结合思想,形成数形统一意识,提高解题能力.“数缺形时少直观,形缺数时难入微.”总之,要把数形结合思想贯穿在数学学习中.数与形及其相互关系是数学研究的基本内容.
【典型例题】
类型一、利用数形结合探究数字的变化规律
/1. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第/个图形需要黑色棋子的个数是 .
/
【思路点拨】
首先计算几个特殊图形,发现:数出每边上的个数,乘以边数,但各个顶点的重复了一次,应再减
去.第1个图形是2×3-3,第2个图形是3×4-4,第3个图形是4×5-5,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n2+2n.
【答案与解析】
第1个图形是三角形,有3条边,每条边上有2个点,重复了3个点,需要黑色棋(2×3-3)个;
第2个图形是四边形,有4条边,每条边上有3个点,重复了4个点,需要黑色棋子(3×4-4)个; 第3个图形是五边形,有5条边,每条边上有4个点,重复了5个点,需要黑色棋子(4×5-5)个; 按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n(n+2). 故答案为n(n+2)=n2+2n.
【总结升华】这样的试题从最简单的图形入手.找出图形中黑点的个数与第n个图形之间的关系,找规
律需要列出算式,一律采用原题中的数据,不要用到计算出来的结果来找规律.
举一反三:
【变式】用棋子按下列方式摆图形,依照此规律,第n个图形比第(n-1)个图形多_____枚棋子.
/
【答案】解:设第n个图形的棋子数为. 第1个图形,S1=1; 第2个图形,S2=1+4; 第3个图形,S3=1+4+7;
第n个图形,Sn=1+4+…+3n-2; 第(n-1)个图形,Sn-1=1+4+…+[3(n-1)-2]; 则第n个图形比第(n-1)个图形多(3n-2)枚棋子.
类型二、 利用数形结合解决数与式的问题
/2.已知实数a、b、c在数轴上的位置如图所示,化简|a+b|-|c-b|的结果是 ( ).
/
A.a+c B.-a-2b+c C.a+2b-c D.-a-c
【思路点拨】
首先从数轴上a、b、c的位置关系可知:c<a<0;b>0且|b|>|a|,接着可得a+b>0,c-b<0,然后即可化简|a+b|-|c-b|可得结果. 具体步骤为:① a,b,c的具体位置,在原点左边的小于0,原点右边的大于0.②比较绝对值的大小.|a|<|c|<|b|.③化简原式中的每一部分,看看绝对值内部(二次根式中的被开方数的底数)的性质,若大于零,直接提出来,若小于零,则取原数的相反数.④进行化简计算,得出最后结果.
【答案与解析】
解:从数轴上a、b、c的位置关系可知:c<a<0;b>0且|b|>|a|,
故a+b>0,c-b<0,
即有|a+b|-|c-b|=a+b+c-b=a+c.
故选A.
【总结升华】
此题主要考查了利用数形结合的思想和方法来解决绝对值与数轴之间的关系,进而考察了非负数的
运用.数轴的特点:从原点向右为正数,向左为负数,及实数与数轴上的点的对应关系.非负数在初中的范围内,有三种形式:绝对值(|a|),完全平方式(a±b)2,二次根式(/.性质:非负数有最小值是0;几个非负数的和等于0,那么每一个非负数都等于0.
类型三、利用数形结合解决代数式的恒等变形问题
/3. 图①是一个边长为/的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
A. / B./
C./ D./
/
【思路点拨】
这是完全平方公式的几何背景,用几何图形来分析和理解完全平方公式的实质.是一个很典型的“数形结合”的例子,用图形的变换来帮助理解代数学中的枯燥无味的数学公式.根据图示可知,阴影部分的面积是边长为(m+n)的正方形的面积减去中间白色的小正方形的面积(m2+n2),即为对角线分别是2m,2n的菱形的面积.据此即可解答.
【答案】B.
【解析】(m+n)2-(m2+n2)=2mn. 故选B.
【总结升华】
本题是利用几何图形的面积来验证(m+n)2-(m2+n2)=2mn,解题关键是利用图形的面积之间的相等关系列等式.
举一反三:
【变式】如图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个空心正方形. (1)你认为图2中的阴影部分的正方形的边长是多少? (2)请用两种不同的方法求出图2中阴影部分的面积;
(3)观察图2,你能写出下列三个代数式:(m+n)2、(m-n)2、mn之间的关系吗?
/
【答案】
解:(1)图②中阴影部分的正方形的边长等于(m-n); (2)(m-n)2;(m+n)2-4mn; (3)(m-n)2=(m+n)2-4mn.
类型四、利用数形结合思想解决极值问题
/4.我们知道:根据二次函数的图象,可以直接确定二次函数的最大(小)值;根据“两点之间,线段最短”,并运用轴对称的性质,可以在一条直线上找到一点,使得此点到这条直线同侧两定点之间的距离之和最短.这种“数形结合”的思想方法,非常有利于解决一些实际问题中的最大(小)值问题.请你尝试解决一下问题: (1)在图1中,抛物线所对应的二次函数的最大值是 _____.
(2)在图2中,相距3km的A、B两镇位于河岸(近似看做直线CD)的同侧,且到河岸的距离AC=1千米,BD=2千米,现要在岸边建一座水塔,直接给两镇送水,为使所用水管的长度最短,请你: ①作图确定水塔的位置; ②求出所需水管的长度(结果用准确值表示). (3)已知x+y=6,求 /的最小值?
此问题可以通过数形结合的方法加以解决,具体步骤如下: ①如图3中,作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA= ____DB= ____. ②在AB上取一点P,可设AP= _____,BP= _____. ③ /的最小值即为线段___和线段_____长度之和的最小值,最小值为 ___
/.
【思路点拨】
(1)利用二次函数的顶点坐标就可得出函数的极值; (2)①延长AC到点E,使CE=AC,连接BE,交直线CD于点P,则点P即为所求; ②过点A作AF⊥BD,垂足为F,过点E作EG⊥BD,交BD的延长线于点G,则有四边形ACDF、CEGD都是矩形,进而利用勾股定理求出即可; (3)①作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA=3,BD=5, ②在AB上取一点P,可设AP=x,BP=y; ③/的最小值即为线段 PC和线段 PD长度之和的最小值,最小值利用勾股定理求出即可.
【答案与解析】
解:(1)抛物线所对应的二次函数的最大值是4; /
(2)①如图所示,点P即为所求. (作法:延长AC到点E,使CE=AC,连接BE,交直线CD于点P,则 点P即为所求. 说明:不必写作法和证明,但要保留作图痕迹;不连接PA不扣分;(延长BD,同样的方法也可以得到P点的位置.) ②过点A作AF⊥BD,垂足为F,过点E作EG⊥BD,交BD的延长线于点G,则有四边形ACDF、CEGD
都是矩形. ∴FD=AC=CE=DG=1,EG=CD=AF. ∵AB=3,BD=2, ∴BF=BD-FD=1,BG=BD+DG=3, ∴在Rt△ABF中,AF2=AB2-BF2=8, ∴AF=2/ EG=2/.
∴在Rt△BEG中,BE2=EG2+BG2=17,
∴BE=/(cm). ∴PA+PB的最小值为/cm. 即所用水管的最短长度为/cm.
(3)图3所示,①作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA=3,BD=5, ②在AB上取一点P,可设AP=x,BP=y, ③/的最小值即为线段 PC和线段 PD长度之和的最小值,
/
∴作C点关于线段AB的对称点C′,连接C′D,过C′点作C′E⊥DB,交BD延长线于点E, ∵AC=BE=3,DB=5,AB=C′E=6, ∴DE=8, /.
∴最小值为10.
故答案为:①4; ②x,y; ③PC,PD,10.
【总结升华】
此题主要考查了函数最值问题与利用轴对称求最短路线问题,结合已知画出图象利用数形结合以及勾股定理是解题关键.
作图题不要求写出作法,但必须保留痕迹.最后点题,即“xx即为所求”.
类型五、利用数形结合思想,解决函数问题
/5.如图,二次函数y=ax2+bx+c的图象开口向上,图象过点(-1,2)和(1,0),且与y轴相交与负半轴.以下结论(1)a>0;(2)b>0;(3)c>0;(4)a+b+c=0;(5)abc<0;(6)2a+b>0;(7)a+c=1;(8)a>1中,正确结论的序号是___________.
/
【思路点拨】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【答案与解析】
解:(1)①由抛物线的开口方向向上,可推出a>0,正确; ②因为对称轴在y轴右侧,对称轴为x=/>0,又因为a>0,∴b<0,错误; ③由抛物线与y轴的交点在y轴的负半轴上,∴c<0,错误; ④由图象可知:当x=1时y=0,∴a+b+c=0,正确;
⑤∵a>0,b<0,c<0,∴abc>0,错误; ⑥由图象可知:对称轴x=/>0且对称轴x=/<1,∴2a+b>0,正确; ⑦由图象可知:当x=-1时y=2,∴a-b+c=2, ---①
当x=1时y=0,∴a+b+c=0, ---②
①+②,得
2a+2c=2,解得 a+c=1,正确; ⑧∵a+c=1,移项得a=1-c,又∵c<0,∴a>1,正确. 故正确结论的序号是①④⑥⑦⑧.
【总结升华】
考查二次函数的解析式、图象,及综合应用相关知识分析问题、解决问题的能力.
二次函数y=ax2+bx+c图象与系数之间的关系: (1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0. (2)b由对称轴和a的符号确定:由对称轴公式x=/判断符号.存在着“左同右异”,即a,b同号.对称轴在y轴的左边,a,b异号,对称轴在y轴的右边. (3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0. (4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.
(5)当x=±1时,ax2+bx+c就变成了a±b+c了.这道题的第7小题:当x=1时,a+b+c=0……①
当x=-1时,a-b+c=2……②,①+②得,2a+2c=2,即a+c=1.
举一反三:
【变式】已知二次函数y=ax2+bx+c的图象如图所示,x=/是该抛物线的对称轴.根据图中所提供的信息,请你写出有关a,b,c的四条结论,并简单说明理由.
【答案】解:①∵开口方向向上,∴a>0, ②∵与y轴的交点为在y轴的正半轴上,∴c>0, ③∵对称轴为x=/>0,∴a、b异号,即b<0, ④∵抛物线与x轴有两个交点,∴b2-4ac>0, ⑤当x=1时,y=a+b+c<0, ⑥当x=-1时,y=a-b+c>0. 结论有:a>0,b<0,c<0,a+b+c<0,a-b+c>0等.
/
中考冲刺:数形结合问题—巩固练习(基础)
【巩固练习】
选择题
1.当k<0时,反比例函数/和一次函数y=kx-k的图象大致是( )
/
2.从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙)。那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A 、/ B、/
C、/ D、/
/
二、 填空题
3. 实数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的序号为____________.
①b+c>0 ②a+b>a+c ③ac<bc ④ab>ac
/
4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: (1)4a+2b+c>0; (2)方程ax2+bx+c=0两根之和小于零; (3)y随x的增大而增大; (4)4a-2b+c<0; (5)b2-4ac<0; (6)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数有______个.
/
三、解答题
5.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么2个小时时血液中含药最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当成人按规定剂量服药后.
(1)分别求出x≤2和x≥2时y与x的函数解析式;
(2)如果每毫升血液中含量为4微克或4微克以上时,在治疗疾病时是有效的,那么这个有效时间有
多长?
/
6.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. / (1)你认为图2中的阴影部分的正方形的边长等于 _____; (2)请用两种不同的方法求图2中阴影部分的面积.① ______②_______; (3)观察图2你能写出下列三个代数式之间的等量关系吗?
(4)运用你所得到的公式,计算若mn=-2,m-n=4,求(m+n)2的值. (5)用完全平方公式和非负数的性质求代数式x2+2x+y2-4y+7的最小值.
7.为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示: (1)分别求出通话费y1,y2与通话时间x之间的函数关系式; (2)请帮用户计算,在一个月内使用哪一种卡便宜.
/
8.如图,一次函数图象与x轴相交于点B,与反比例函数图象相交于点A(1,-6);△AOB的面积为6.求一次函数和反比例函数的解析式.
/
9.请同学们仔细阅读如图所示的计算机程序框架图,回答下列问题: (1)如果输入值为2,那么输出值是多少? (2)若要使输入的x的值只经过一次运行就能输出结果,求x的取值范围; (3)若要使开始输入的x的值经过两次运行才能输出结果,那么x的取值范围又是多少?
/
10.观察如图所包含规律(图中三角形均是直角三角形,且一条直角边始终为1,四边形均为正方形.S1,S2,S3,…Sn依次表示正方形的面积,每个正方形边长与它左边相邻的直角三角形斜边相等),再回答下列问题. (1)填表:
直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
…
(2)当s1+s2+s3+s4+…+sn=465时,求n.
/
11.某报社为了了解读者对该报社一种报纸四个版面的认可情况,对读者做了一次问卷凋查,要求读者选出自己最喜欢的一个版面,并将调查结果绘制成如下的统计图,请你根据图中提供的信息解答下列问题. (1)在这次活动中一共调查了多少读者? (2)在扇形统计图中,计算第一版所在扇形的圆心角度数; (3)请你求出喜欢第四版的人数,并将条形统计图补充完整.
/
【答案与解析】
一、选择题
1.【答案】B;
2.【答案】D;
二、 填空题
3.【答案】②③④;
4.【答案】1;
三、 解答题
5.【答案与解析】
解:(1)当x≤2时,设y=kx, 把(2,6)代入上式,得k=3, ∴x≤2时,y=3x; 当x≥2时,设y=kx+b, 把(2,6),(10,3)代入上式,得
k=/,b=/ ∴x≥2时,y=/x+/
(2)把y=4代入y=3x,得x1=/ 把y=4代入y=/x+/ 得x2=/
则x2-x1=6(小时).
答:这个有效时间为6小时.
6.【答案与解析】
解:(1)由图可知,阴影部分小正方形的边长为:m-n;
(2)根据正方形的面积公式,阴影部分的面积为(m-n)2,
还可以表示为(m+n)2-4mn;
(3)根据阴影部分的面积相等,(m-n)2=(m+n)2-4mn; (4)∵mn=-2,m-n=4, ∴(m+n)2=(m-n)2+4mn=42+4×(-2)=16-8=8;
(5)x2+2x+y2-4y+7, =x2+2x+1+y2-4y+4+2, =(x+1)2+(y-2)2+2, ∵(x+1)2≥0,(y-2)2≥0, ∴(x+1)2+(y-2)2≥2, ∴当x=-1,y=2时,代数式x2+2x+y2-4y+7的最小值是2. 故答案为:(1)m-n;(2)(m-n)2,(m+n)2-4mn;(3)(m-n)2=(m+n)2-4mn.(4) 8 (5) 最
小值是2.
7.【答案与解析】
解:(1)设y1=kx+b,将(0,29),(30,35)代入,
解得k=/,b=29,∴y1=/x+29,
又24×60×30=43200(min)(属于隐含条件)
∴y1=/x+29 (0≤x≤43200),
同样求得y2=/x (0≤x≤43200);
(2)当y1=y2时,
/x+29=/x,
x=/;
当y1<y2时,
/x+29</x, x>/.
所以,当通话时间等于/min时,两种卡的收费一致, 当通话时间小于/min时,“如意卡便宜”, 当通话时间大于/min时,“便民卡”便宜.
8.【答案与解析】
解:设反比例函数解析式为:y=/(k≠0), ∵点A(1,-6)在反比例函数图象上 ∴k=1×(-6)=-6, 即反比例函数关系式为y=-/, ∵△AOB的面积为6. ∴/×OB×6=6, ∴OB=2, ∴B(-2,0), 设一次函数解析式为:y=kx+b, ∵图象经过A(1,-6),B(-2,0), ∴/
解得:/ ∴一次函数解析式为:y=-2x-4.
9.【答案与解析】
解:(1)依据题中的计算程序列出算式:3×2+1, ∵3×2+1=7,7<9, ∴应该按照计算程序继续计算,3×7+1=22>9, ∴如果输入值为2,那么输出值是22.
(2)依题意,有3x+1>9, 解得x>/;
(3)依题意,有/
解得/<x≤/.
10.【答案与解析】
解:(1)/,
/,
直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
/
/
2
…
(2)S1=(/)2=2, S2=(/)2=3, S3=22=4, S4=(/)2=5,…….. Sn=(/)2=n+1; 由s1+s2+s3+s4+…+sn=465可得: 1+2+3+4+5+…+n=465,
/(1+n) ×n=465
解得:n=-31(不合题意舍去)或n=30, 故:n=30.
11.【答案与解析】
解:(1)这次活动中一共调查了500÷10%=5000(人); (2)第一版所在扇形的圆心角度数=360°×(1-20%-40%-10%)=108°; (3)喜欢第四版的人数是: 5000×20%=1000(人),如下图所示:
/ /
中考冲刺:数形结合问题—知识讲解(基础)
【中考展望】
1.用数形结合的思想解题可分两类:
(1)利用几何图形的直观性表示数的问题,它常借用数轴、函数图象等;
(2)运用数量关系来研究几何图形问题,常常要建立方程(组)或建立函数关系式等.
2. 热点内容:
在初中教材中,“数”的常见表现形式为: 实数、代数式、函数和不等式等,而“形”的常见表现形式为: 直线型、角、三角形、四边形、多边形、圆、抛物线、相似、勾股定理等.在直角坐标系下,一次函数图象对应一条直线,二次函数的图像对应着一条抛物线,这些都是初中数学的重要内容. 【方法点拨】
数形结合:就是通过数与形之间的对应和转化来解决数学问题,它包含“以形助数”和“以数解形”两个方面.利用它可使复杂问题简单化,抽象问题具体化,它兼有“数的严谨”与“形的直观”之长,是优化解题过程的重要途径之一,是一种基本的数学方法. 数形结合解题基本思路:“数”和“形”是数学中两个最基本的概念, 每一个几何图形中都蕴含着与它们的形状、大小、位置密切相关的数量关系;反之,数量关系又常常可以通过几何图形做出直观地反映和描述.数形结合的实质就是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合起来,在解决代数问题时,想到它的图形,从而启发思维,找到解题之路;或者在研究图形时,利用代数的知识,解决几何的问题.实现了抽象概念与具体图形的联系和转化,化难为易,化抽象为直观.
特别是二次函数,不仅是学生学习的难点之一,同时也使数形结合的思想方法在中学数学中得到最充分体现.在平面直角坐标系中,二次函数图象的开口方向、顶点坐标、对称轴以及与坐标轴的交点等都与其系数a,b,c密不可分.事实上,a的符号决定抛物线的开口方向,b与a 一起决定抛物线的对称轴的位置, c 决定了抛物线与y 轴的交点位置,与a、b 一起决定抛物线顶点坐标的纵坐标,抛物线图形的平移,只是顶点坐标发生变化,其实从代数的角度看是b、c 的有关变化.
在日常的数学学习中应注意养成数形相依的观念,有意识培养数形结合思想,形成数形统一意识,提高解题能力.“数缺形时少直观,形缺数时难入微.”总之,要把数形结合思想贯穿在数学学习中.数与形及其相互关系是数学研究的基本内容.
【典型例题】
类型一、利用数形结合探究数字的变化规律
/1. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第/个图形需要黑色棋子的个数是 .
/
【思路点拨】
首先计算几个特殊图形,发现:数出每边上的个数,乘以边数,但各个顶点的重复了一次,应再减
去.第1个图形是2×3-3,第2个图形是3×4-4,第3个图形是4×5-5,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n2+2n.
【答案与解析】
第1个图形是三角形,有3条边,每条边上有2个点,重复了3个点,需要黑色棋(2×3-3)个;
第2个图形是四边形,有4条边,每条边上有3个点,重复了4个点,需要黑色棋子(3×4-4)个; 第3个图形是五边形,有5条边,每条边上有4个点,重复了5个点,需要黑色棋子(4×5-5)个; 按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)-(n+2)=n(n+2). 故答案为n(n+2)=n2+2n.
【总结升华】这样的试题从最简单的图形入手.找出图形中黑点的个数与第n个图形之间的关系,找规
律需要列出算式,一律采用原题中的数据,不要用到计算出来的结果来找规律.
举一反三:
【变式】用棋子按下列方式摆图形,依照此规律,第n个图形比第(n-1)个图形多_____枚棋子.
/
【答案】解:设第n个图形的棋子数为. 第1个图形,S1=1; 第2个图形,S2=1+4; 第3个图形,S3=1+4+7;
第n个图形,Sn=1+4+…+3n-2; 第(n-1)个图形,Sn-1=1+4+…+[3(n-1)-2]; 则第n个图形比第(n-1)个图形多(3n-2)枚棋子.
类型二、 利用数形结合解决数与式的问题
/2.已知实数a、b、c在数轴上的位置如图所示,化简|a+b|-|c-b|的结果是 ( ).
/
A.a+c B.-a-2b+c C.a+2b-c D.-a-c
【思路点拨】
首先从数轴上a、b、c的位置关系可知:c<a<0;b>0且|b|>|a|,接着可得a+b>0,c-b<0,然后即可化简|a+b|-|c-b|可得结果. 具体步骤为:① a,b,c的具体位置,在原点左边的小于0,原点右边的大于0.②比较绝对值的大小.|a|<|c|<|b|.③化简原式中的每一部分,看看绝对值内部(二次根式中的被开方数的底数)的性质,若大于零,直接提出来,若小于零,则取原数的相反数.④进行化简计算,得出最后结果.
【答案与解析】
解:从数轴上a、b、c的位置关系可知:c<a<0;b>0且|b|>|a|,
故a+b>0,c-b<0,
即有|a+b|-|c-b|=a+b+c-b=a+c.
故选A.
【总结升华】
此题主要考查了利用数形结合的思想和方法来解决绝对值与数轴之间的关系,进而考察了非负数的
运用.数轴的特点:从原点向右为正数,向左为负数,及实数与数轴上的点的对应关系.非负数在初中的范围内,有三种形式:绝对值(|a|),完全平方式(a±b)2,二次根式(/.性质:非负数有最小值是0;几个非负数的和等于0,那么每一个非负数都等于0.
类型三、利用数形结合解决代数式的恒等变形问题
/3. 图①是一个边长为/的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
A. / B./
C./ D./
/
【思路点拨】
这是完全平方公式的几何背景,用几何图形来分析和理解完全平方公式的实质.是一个很典型的“数形结合”的例子,用图形的变换来帮助理解代数学中的枯燥无味的数学公式.根据图示可知,阴影部分的面积是边长为(m+n)的正方形的面积减去中间白色的小正方形的面积(m2+n2),即为对角线分别是2m,2n的菱形的面积.据此即可解答.
【答案】B.
【解析】(m+n)2-(m2+n2)=2mn. 故选B.
【总结升华】
本题是利用几何图形的面积来验证(m+n)2-(m2+n2)=2mn,解题关键是利用图形的面积之间的相等关系列等式.
举一反三:
【变式】如图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个空心正方形. (1)你认为图2中的阴影部分的正方形的边长是多少? (2)请用两种不同的方法求出图2中阴影部分的面积;
(3)观察图2,你能写出下列三个代数式:(m+n)2、(m-n)2、mn之间的关系吗?
/
【答案】
解:(1)图②中阴影部分的正方形的边长等于(m-n); (2)(m-n)2;(m+n)2-4mn; (3)(m-n)2=(m+n)2-4mn.
类型四、利用数形结合思想解决极值问题
/4.我们知道:根据二次函数的图象,可以直接确定二次函数的最大(小)值;根据“两点之间,线段最短”,并运用轴对称的性质,可以在一条直线上找到一点,使得此点到这条直线同侧两定点之间的距离之和最短.这种“数形结合”的思想方法,非常有利于解决一些实际问题中的最大(小)值问题.请你尝试解决一下问题: (1)在图1中,抛物线所对应的二次函数的最大值是 _____.
(2)在图2中,相距3km的A、B两镇位于河岸(近似看做直线CD)的同侧,且到河岸的距离AC=1千米,BD=2千米,现要在岸边建一座水塔,直接给两镇送水,为使所用水管的长度最短,请你: ①作图确定水塔的位置; ②求出所需水管的长度(结果用准确值表示). (3)已知x+y=6,求 /的最小值?
此问题可以通过数形结合的方法加以解决,具体步骤如下: ①如图3中,作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA= ____DB= ____. ②在AB上取一点P,可设AP= _____,BP= _____. ③ /的最小值即为线段___和线段_____长度之和的最小值,最小值为 ___
/.
【思路点拨】
(1)利用二次函数的顶点坐标就可得出函数的极值; (2)①延长AC到点E,使CE=AC,连接BE,交直线CD于点P,则点P即为所求; ②过点A作AF⊥BD,垂足为F,过点E作EG⊥BD,交BD的延长线于点G,则有四边形ACDF、CEGD都是矩形,进而利用勾股定理求出即可; (3)①作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA=3,BD=5, ②在AB上取一点P,可设AP=x,BP=y; ③/的最小值即为线段 PC和线段 PD长度之和的最小值,最小值利用勾股定理求出即可.
【答案与解析】
解:(1)抛物线所对应的二次函数的最大值是4; /
(2)①如图所示,点P即为所求. (作法:延长AC到点E,使CE=AC,连接BE,交直线CD于点P,则 点P即为所求. 说明:不必写作法和证明,但要保留作图痕迹;不连接PA不扣分;(延长BD,同样的方法也可以得到P点的位置.) ②过点A作AF⊥BD,垂足为F,过点E作EG⊥BD,交BD的延长线于点G,则有四边形ACDF、CEGD
都是矩形. ∴FD=AC=CE=DG=1,EG=CD=AF. ∵AB=3,BD=2, ∴BF=BD-FD=1,BG=BD+DG=3, ∴在Rt△ABF中,AF2=AB2-BF2=8, ∴AF=2/ EG=2/.
∴在Rt△BEG中,BE2=EG2+BG2=17,
∴BE=/(cm). ∴PA+PB的最小值为/cm. 即所用水管的最短长度为/cm.
(3)图3所示,①作线段AB=6,分别过点A、B,作CA⊥AB,DB⊥AB,使得CA=3,BD=5, ②在AB上取一点P,可设AP=x,BP=y, ③/的最小值即为线段 PC和线段 PD长度之和的最小值,
/
∴作C点关于线段AB的对称点C′,连接C′D,过C′点作C′E⊥DB,交BD延长线于点E, ∵AC=BE=3,DB=5,AB=C′E=6, ∴DE=8, /.
∴最小值为10.
故答案为:①4; ②x,y; ③PC,PD,10.
【总结升华】
此题主要考查了函数最值问题与利用轴对称求最短路线问题,结合已知画出图象利用数形结合以及勾股定理是解题关键.
作图题不要求写出作法,但必须保留痕迹.最后点题,即“xx即为所求”.
类型五、利用数形结合思想,解决函数问题
/5.如图,二次函数y=ax2+bx+c的图象开口向上,图象过点(-1,2)和(1,0),且与y轴相交与负半轴.以下结论(1)a>0;(2)b>0;(3)c>0;(4)a+b+c=0;(5)abc<0;(6)2a+b>0;(7)a+c=1;(8)a>1中,正确结论的序号是___________.
/
【思路点拨】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【答案与解析】
解:(1)①由抛物线的开口方向向上,可推出a>0,正确; ②因为对称轴在y轴右侧,对称轴为x=/>0,又因为a>0,∴b<0,错误; ③由抛物线与y轴的交点在y轴的负半轴上,∴c<0,错误; ④由图象可知:当x=1时y=0,∴a+b+c=0,正确;
⑤∵a>0,b<0,c<0,∴abc>0,错误; ⑥由图象可知:对称轴x=/>0且对称轴x=/<1,∴2a+b>0,正确; ⑦由图象可知:当x=-1时y=2,∴a-b+c=2, ---①
当x=1时y=0,∴a+b+c=0, ---②
①+②,得
2a+2c=2,解得 a+c=1,正确; ⑧∵a+c=1,移项得a=1-c,又∵c<0,∴a>1,正确. 故正确结论的序号是①④⑥⑦⑧.
【总结升华】
考查二次函数的解析式、图象,及综合应用相关知识分析问题、解决问题的能力.
二次函数y=ax2+bx+c图象与系数之间的关系: (1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0. (2)b由对称轴和a的符号确定:由对称轴公式x=/判断符号.存在着“左同右异”,即a,b同号.对称轴在y轴的左边,a,b异号,对称轴在y轴的右边. (3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0. (4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.
(5)当x=±1时,ax2+bx+c就变成了a±b+c了.这道题的第7小题:当x=1时,a+b+c=0……①
当x=-1时,a-b+c=2……②,①+②得,2a+2c=2,即a+c=1.
举一反三:
【变式】已知二次函数y=ax2+bx+c的图象如图所示,x=/是该抛物线的对称轴.根据图中所提供的信息,请你写出有关a,b,c的四条结论,并简单说明理由.
【答案】解:①∵开口方向向上,∴a>0, ②∵与y轴的交点为在y轴的正半轴上,∴c>0, ③∵对称轴为x=/>0,∴a、b异号,即b<0, ④∵抛物线与x轴有两个交点,∴b2-4ac>0, ⑤当x=1时,y=a+b+c<0, ⑥当x=-1时,y=a-b+c>0. 结论有:a>0,b<0,c<0,a+b+c<0,a-b+c>0等.
/
中考冲刺:数形结合问题—巩固练习(基础)
【巩固练习】
选择题
1.当k<0时,反比例函数/和一次函数y=kx-k的图象大致是( )
/
2.从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙)。那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A 、/ B、/
C、/ D、/
/
二、 填空题
3. 实数a、b、c在数轴上的对应点的位置如图所示,下列式子中正确的序号为____________.
①b+c>0 ②a+b>a+c ③ac<bc ④ab>ac
/
4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: (1)4a+2b+c>0; (2)方程ax2+bx+c=0两根之和小于零; (3)y随x的增大而增大; (4)4a-2b+c<0; (5)b2-4ac<0; (6)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数有______个.
/
三、解答题
5.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么2个小时时血液中含药最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当成人按规定剂量服药后.
(1)分别求出x≤2和x≥2时y与x的函数解析式;
(2)如果每毫升血液中含量为4微克或4微克以上时,在治疗疾病时是有效的,那么这个有效时间有
多长?
/
6.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. / (1)你认为图2中的阴影部分的正方形的边长等于 _____; (2)请用两种不同的方法求图2中阴影部分的面积.① ______②_______; (3)观察图2你能写出下列三个代数式之间的等量关系吗?
(4)运用你所得到的公式,计算若mn=-2,m-n=4,求(m+n)2的值. (5)用完全平方公式和非负数的性质求代数式x2+2x+y2-4y+7的最小值.
7.为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示: (1)分别求出通话费y1,y2与通话时间x之间的函数关系式; (2)请帮用户计算,在一个月内使用哪一种卡便宜.
/
8.如图,一次函数图象与x轴相交于点B,与反比例函数图象相交于点A(1,-6);△AOB的面积为6.求一次函数和反比例函数的解析式.
/
9.请同学们仔细阅读如图所示的计算机程序框架图,回答下列问题: (1)如果输入值为2,那么输出值是多少? (2)若要使输入的x的值只经过一次运行就能输出结果,求x的取值范围; (3)若要使开始输入的x的值经过两次运行才能输出结果,那么x的取值范围又是多少?
/
10.观察如图所包含规律(图中三角形均是直角三角形,且一条直角边始终为1,四边形均为正方形.S1,S2,S3,…Sn依次表示正方形的面积,每个正方形边长与它左边相邻的直角三角形斜边相等),再回答下列问题. (1)填表:
直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
…
(2)当s1+s2+s3+s4+…+sn=465时,求n.
/
11.某报社为了了解读者对该报社一种报纸四个版面的认可情况,对读者做了一次问卷凋查,要求读者选出自己最喜欢的一个版面,并将调查结果绘制成如下的统计图,请你根据图中提供的信息解答下列问题. (1)在这次活动中一共调查了多少读者? (2)在扇形统计图中,计算第一版所在扇形的圆心角度数; (3)请你求出喜欢第四版的人数,并将条形统计图补充完整.
/
【答案与解析】
一、选择题
1.【答案】B;
2.【答案】D;
二、 填空题
3.【答案】②③④;
4.【答案】1;
三、 解答题
5.【答案与解析】
解:(1)当x≤2时,设y=kx, 把(2,6)代入上式,得k=3, ∴x≤2时,y=3x; 当x≥2时,设y=kx+b, 把(2,6),(10,3)代入上式,得
k=/,b=/ ∴x≥2时,y=/x+/
(2)把y=4代入y=3x,得x1=/ 把y=4代入y=/x+/ 得x2=/
则x2-x1=6(小时).
答:这个有效时间为6小时.
6.【答案与解析】
解:(1)由图可知,阴影部分小正方形的边长为:m-n;
(2)根据正方形的面积公式,阴影部分的面积为(m-n)2,
还可以表示为(m+n)2-4mn;
(3)根据阴影部分的面积相等,(m-n)2=(m+n)2-4mn; (4)∵mn=-2,m-n=4, ∴(m+n)2=(m-n)2+4mn=42+4×(-2)=16-8=8;
(5)x2+2x+y2-4y+7, =x2+2x+1+y2-4y+4+2, =(x+1)2+(y-2)2+2, ∵(x+1)2≥0,(y-2)2≥0, ∴(x+1)2+(y-2)2≥2, ∴当x=-1,y=2时,代数式x2+2x+y2-4y+7的最小值是2. 故答案为:(1)m-n;(2)(m-n)2,(m+n)2-4mn;(3)(m-n)2=(m+n)2-4mn.(4) 8 (5) 最
小值是2.
7.【答案与解析】
解:(1)设y1=kx+b,将(0,29),(30,35)代入,
解得k=/,b=29,∴y1=/x+29,
又24×60×30=43200(min)(属于隐含条件)
∴y1=/x+29 (0≤x≤43200),
同样求得y2=/x (0≤x≤43200);
(2)当y1=y2时,
/x+29=/x,
x=/;
当y1<y2时,
/x+29</x, x>/.
所以,当通话时间等于/min时,两种卡的收费一致, 当通话时间小于/min时,“如意卡便宜”, 当通话时间大于/min时,“便民卡”便宜.
8.【答案与解析】
解:设反比例函数解析式为:y=/(k≠0), ∵点A(1,-6)在反比例函数图象上 ∴k=1×(-6)=-6, 即反比例函数关系式为y=-/, ∵△AOB的面积为6. ∴/×OB×6=6, ∴OB=2, ∴B(-2,0), 设一次函数解析式为:y=kx+b, ∵图象经过A(1,-6),B(-2,0), ∴/
解得:/ ∴一次函数解析式为:y=-2x-4.
9.【答案与解析】
解:(1)依据题中的计算程序列出算式:3×2+1, ∵3×2+1=7,7<9, ∴应该按照计算程序继续计算,3×7+1=22>9, ∴如果输入值为2,那么输出值是22.
(2)依题意,有3x+1>9, 解得x>/;
(3)依题意,有/
解得/<x≤/.
10.【答案与解析】
解:(1)/,
/,
直角边
A1B1
A2B2
A3B3
A4B4
…
AnBn
长度
1
/
/
2
…
(2)S1=(/)2=2, S2=(/)2=3, S3=22=4, S4=(/)2=5,…….. Sn=(/)2=n+1; 由s1+s2+s3+s4+…+sn=465可得: 1+2+3+4+5+…+n=465,
/(1+n) ×n=465
解得:n=-31(不合题意舍去)或n=30, 故:n=30.
11.【答案与解析】
解:(1)这次活动中一共调查了500÷10%=5000(人); (2)第一版所在扇形的圆心角度数=360°×(1-20%-40%-10%)=108°; (3)喜欢第四版的人数是: 5000×20%=1000(人),如下图所示:
/ /
同课章节目录
