人教版八年级上册数学12.2全等三角形的判定同步练习(解析版)
文档属性
| 名称 | 人教版八年级上册数学12.2全等三角形的判定同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 540.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 07:29:10 | ||
图片预览


文档简介
人教版八年级上册数学12.2全等三角形的判定同步练习
一.选择题(共16小题)
1.在下列条件中,可以判定两个三角形全等的条件是( )
A.三个角对应相等
B.一边对应相等且这边上的高也对应相等
C.两边对应相等且其中一边上的中线也对应相等
D.两边对应相等且其中一边的对角也对应相等
2.如图,在正方形网格上有五个三角形,其中与△ABC全等(不包括本身)的三角形有( )
A.4个 B.3个 C.2个 D.1个
3.如图,已知AB=AC,BD⊥AC于D,CE⊥AB于E,图中全等三角形的组数是( )
A.5 B.4 C.3 D.2
4.如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
A.AE=CD B.AE>CD C.AE<CD D.无法确定
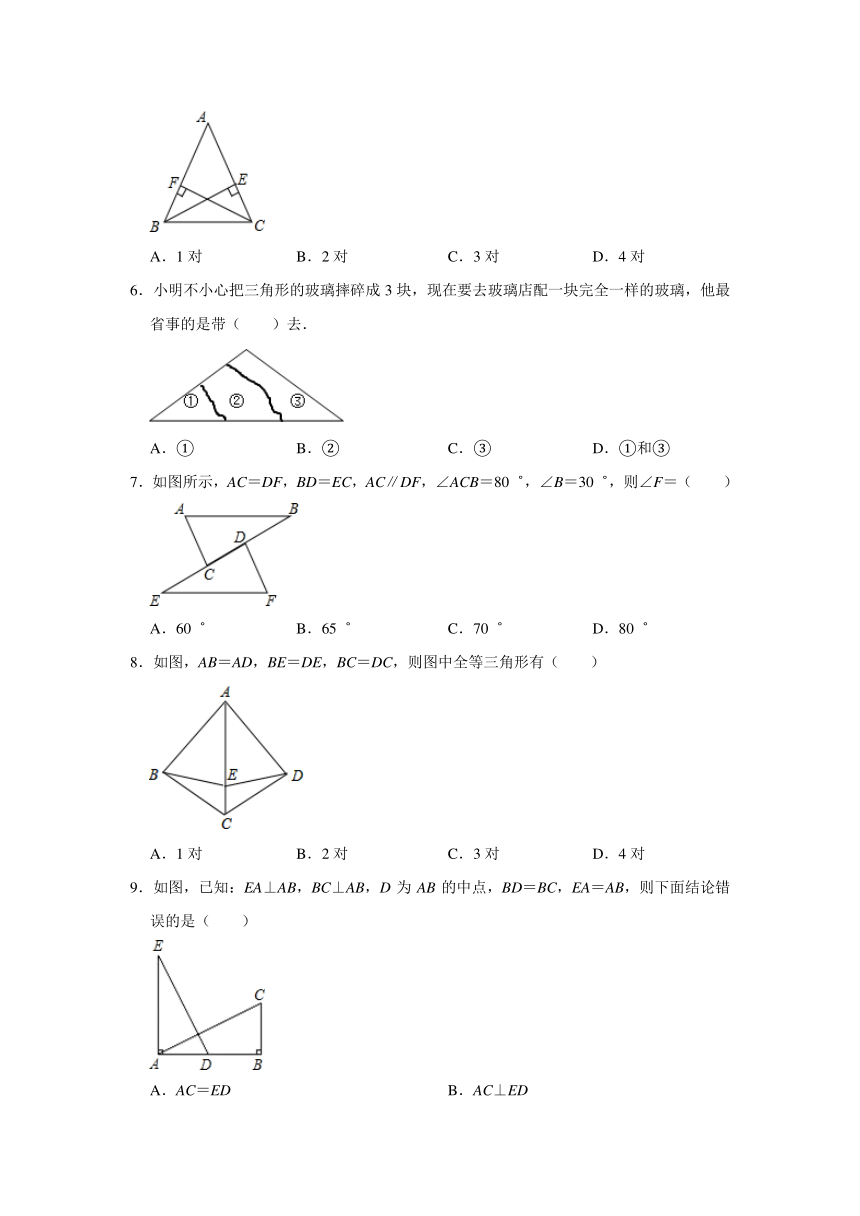
5.如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
6.小明不小心把三角形的玻璃摔碎成3块,现在要去玻璃店配一块完全一样的玻璃,他最省事的是带( )去.
A.① B.② C.③ D.①和③
7.如图所示,AC=DF,BD=EC,AC∥DF,∠ACB=80゜,∠B=30゜,则∠F=( )
A.60゜ B.65゜ C.70゜ D.80゜
8.如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
9.如图,已知:EA⊥AB,BC⊥AB,D为AB的中点,BD=BC,EA=AB,则下面结论错误的是( )
A.AC=ED B.AC⊥ED
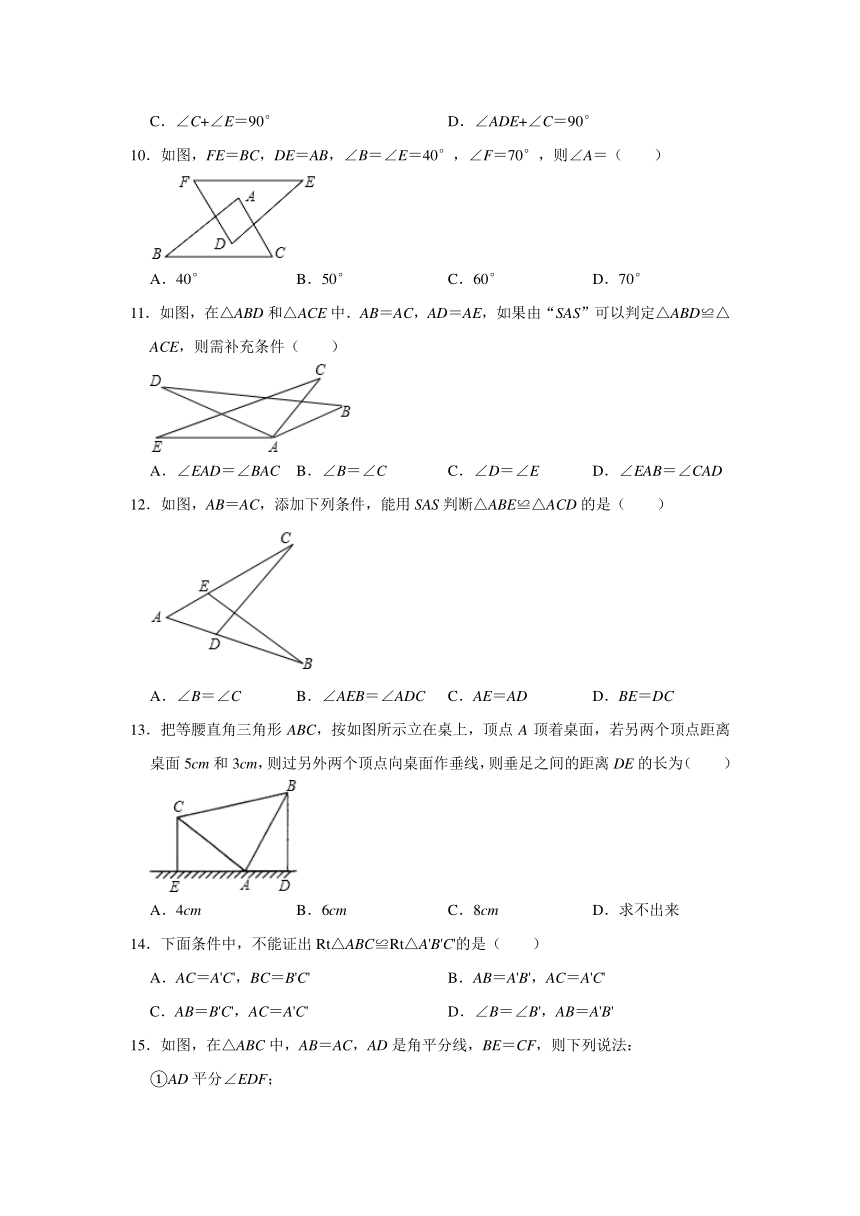
C.∠C+∠E=90° D.∠ADE+∠C=90°
10.如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )
A.40° B.50° C.60° D.70°
11.如图,在△ABD和△ACE中.AB=AC,AD=AE,如果由“SAS”可以判定△ABD≌△ACE,则需补充条件( )
A.∠EAD=∠BAC B.∠B=∠C C.∠D=∠E D.∠EAB=∠CAD
12.如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
13.把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
14.下面条件中,不能证出Rt△ABC≌Rt△A'B'C'的是( )
A.AC=A'C',BC=B'C' B.AB=A'B',AC=A'C'
C.AB=B'C',AC=A'C' D.∠B=∠B',AB=A'B'
15.如图,在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法:
①AD平分∠EDF;
②△EBD≌△FCD;
③AD⊥BC;
④BD=CD.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
16.已知:如图,在等边三角形ABC,AD=BE=CF,D,E,F不是各边的中点,AE,BF,CD分别交于P,M,N在每一组全等三角形中,有三个三角形全等,在图中全等三角形的组数是( )
A.5 B.4 C.3 D.2
二.填空题(共11小题)
17.如图,Rt△ABC和Rt△DEF,∠C=∠F=90°
(1)若∠A=∠D,BC=EF,则Rt△ABC≌Rt△DEF的依据是 .
(2)若∠A=∠D,AC=DF,则Rt△ABC≌Rt△DEF的依据是 .
(3)若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF的依据是 .
(4)若AC=DF,AB=DE,则Rt△ABC≌Rt△DEF的依据是 .
(5)若AC=DF,CB=FE,则Rt△ABC≌Rt△DEF的依据是 .
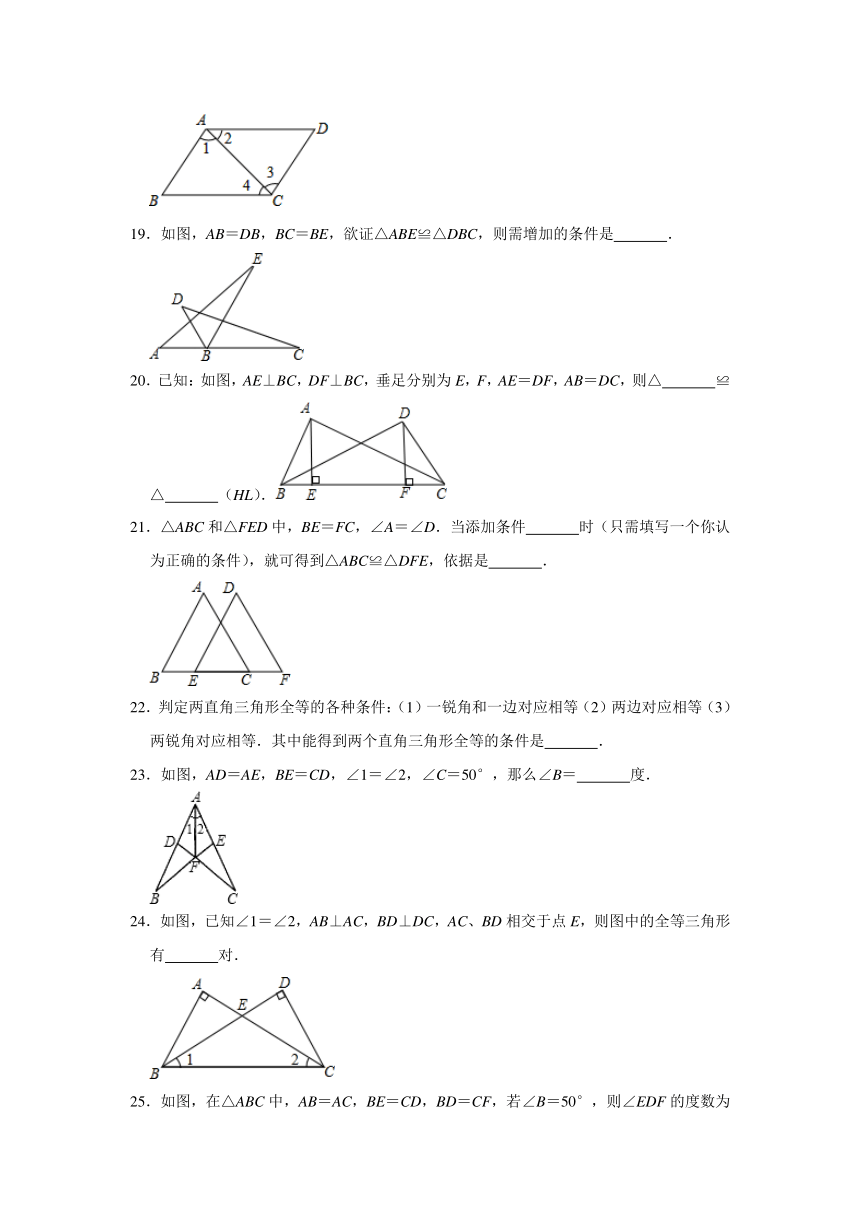
18.已知:如图,∠1=∠3,∠2=∠4,则△ ≌△ .
19.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需增加的条件是 .
20.已知:如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△ ≌△ (HL).
21.△ABC和△FED中,BE=FC,∠A=∠D.当添加条件 时(只需填写一个你认为正确的条件),就可得到△ABC≌△DFE,依据是 .
22.判定两直角三角形全等的各种条件:(1)一锐角和一边对应相等(2)两边对应相等(3)两锐角对应相等.其中能得到两个直角三角形全等的条件是 .
23.如图,AD=AE,BE=CD,∠1=∠2,∠C=50°,那么∠B= 度.
24.如图,已知∠1=∠2,AB⊥AC,BD⊥DC,AC、BD相交于点E,则图中的全等三角形有 对.
25.如图,在△ABC中,AB=AC,BE=CD,BD=CF,若∠B=50°,则∠EDF的度数为 度.
26.有一锐角和斜边对应相等的两个直角三角形 ,理由是 .
27.如图,已知在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE,垂足分别是D、E,若CE=3,BD=7,则DE= .
三.解答题(共11小题)
28.如图,在△ABC和△DEF中,B,E,C,F在同一条直线上.下面给出四个论断:
①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF.
任选三个作为已知条件,余下一个作为结论,可得到几个命题?其中真命题有几个?分别给出证明.
29.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是?(只需写一个,不添加辅助线)
30.如图,已知△ABC中,∠BAC=90°,AB=AC,点P为BC边上一动点(BP<CP),分别过B、C作BE⊥AP于E,CF⊥AP于F.
(1)求证:EF=CF﹣BE.
(2)若点P为BC延长线上一点,其它条件不变,则线段BE、CF、EF是否存在某种确定的数量关系?画图并直接写出你的结论.
31.如图,在△ABC中,∠C=90゜,D是AB上一点,DM⊥AB,且DM=AC,过M作ME∥BC交AB于E.求证:ME=AB.
32.如图,点A,C,B,D在同一条直线上,AC=BD,AM=CN,BM=DN,求证:AM∥CN,BM∥DN.
33.已知:如图,AD是△ABC的高,E是AD上一点.AD=BD,DE=DC,
求证:(1)∠1=∠C.(2)BE⊥AC.
34.已知:如图,AD∥BC,∠B=∠D.求证:△ADC≌△CBA.
35.已知:如图所示,E是AB延长线上的一点,AE=AC,AD平分∠BAC交BC于点D,BD=BE.
求证:∠ABC=2∠C.
36.已知:如图,M是AB的中点,MC=MD,∠1=∠2
证明:AC=BD.
37.已知,如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,请说明AC=AB+BD.
方法一:截长法:(图2)
在较长的线段上截一条线段等于较短线段.
方法二:补短法:(图3)
延长较短线段和较长线段相等.
38.如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC.
求证:OB=OC.
人教版八年级上册数学12.2全等三角形的判定同步练习
参考答案
一.选择题(共16小题)
1.在下列条件中,可以判定两个三角形全等的条件是( )
A.三个角对应相等
B.一边对应相等且这边上的高也对应相等
C.两边对应相等且其中一边上的中线也对应相等
D.两边对应相等且其中一边的对角也对应相等
【解答】解:A、错误,三个角相等,无法判断三角形全等;
B、错误,不符合全等的条件;
C、正确,符合SSS;
D、错误,不符合全等的条件.
故选:C.
2.如图,在正方形网格上有五个三角形,其中与△ABC全等(不包括本身)的三角形有( )
A.4个 B.3个 C.2个 D.1个
【解答】解:根据SSS,可以判定图中有两个三角形与△ABC相似.
故选:C.
3.如图,已知AB=AC,BD⊥AC于D,CE⊥AB于E,图中全等三角形的组数是( )
A.5 B.4 C.3 D.2
【解答】解:在△ABD和△ACE中,,
∴△ABD≌△ACE(AAS),
∴∠B=∠C,AD=AE,
∴CD=BE,
在△BOE和△COD中,,
∴△BOE≌△COD(ASA),
∴OB=OC,OE=OD,
因此△AOD≌△AOE(SAS),
同理:△AOC≌△AOB,
故选:B.
4.如图,△ABC与△BDE都是等边三角形,则AE与CD的大小关系为( )
A.AE=CD B.AE>CD C.AE<CD D.无法确定
【解答】解:AE=CD,理由如下:
∵△ABC和△BDE分别是等边三角形,
∴AB=CB,BE=BD,
∴∠ABC=∠DBE=60°,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴AE=CD.
故选:A.
5.如图所示,BE⊥AC,CF⊥AB,垂足分别是E.F,若BE=CF,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
【解答】解:①△BCF≌△CBE
∵BE⊥AC,CF⊥AB
∴∠CFB=∠BEC=90°
∵BE=CF,BC=BC
∴△BCF≌△CBE(HL);
②△ABE≌△ACF
∵BE⊥AC,CF⊥AB
∴∠AFC=∠AEB=90°
∵BE=CF,∠A=∠A,
∴△ABE≌△ACF(HL);
③BOF≌△COE
设BE与CF相交于点O,
∵BE⊥AC,CF⊥AB
∴∠OFB=∠OEC
∵BF=CE,∠BOF=∠COE
∴△BOF≌△COE(AAS).
故选:C.
6.小明不小心把三角形的玻璃摔碎成3块,现在要去玻璃店配一块完全一样的玻璃,他最省事的是带( )去.
A.① B.② C.③ D.①和③
【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
第二块,仅保留了原三角形的一部分边,所以该块不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:C.
7.如图所示,AC=DF,BD=EC,AC∥DF,∠ACB=80゜,∠B=30゜,则∠F=( )
A.60゜ B.65゜ C.70゜ D.80゜
【解答】解:∵BD=EC,
∴BD+CD=EC+DC,
∴BC=DE,
∵AC∥DF,
∴∠ACB=∠FDE,
在△ACB和△FDE中,
,
∴△ACB≌△FDE(SAS),
∴∠E=∠B=30°,∠FDE=∠ACB=80°,
∴∠F=180°﹣∠B﹣∠FDE=70°,
故选:C.
8.如图,AB=AD,BE=DE,BC=DC,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
【解答】解:在△ABE和△ADE中,
,
∴△ABE≌△ADE(SSS);
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS);
在△BCE和△DCE中,
,
∴△BCE≌△DCE(SSS);
综上可得共有3对全等图形.
故选:C.
9.如图,已知:EA⊥AB,BC⊥AB,D为AB的中点,BD=BC,EA=AB,则下面结论错误的是( )
A.AC=ED B.AC⊥ED
C.∠C+∠E=90° D.∠ADE+∠C=90°
【解答】解:∵D为AB的中点,BD=BC,
∴AD=BC.
∵EA⊥AB,BC⊥AB,EA=AB,
∴△ADE≌△ACB.
A、根据△ADE≌△ACB,得AC=ED.故该选项正确;
B、根据△ADE≌△ACB,得∠E=∠BAC,又∠E+∠ADE=90°,则∠BAC+∠ADE=90°,则AC⊥ED.故该选项正确;
C、根据△ADE≌△ACB,得∠E=∠BAC,又∠BAC+∠C=90°,则∠C+∠E=90°.故该选项正确;
D、根据△ADE≌△ACB,得∠C=∠ADE.故该选项错误.
故选:D.
10.如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )
A.40° B.50° C.60° D.70°
【解答】解:在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠C=∠F=70°.
∵∠A+∠B+∠C=180°,
∴∠A=180°﹣∠B﹣∠C
=180°﹣40°﹣70°=70°,
故选:D.
11.如图,在△ABD和△ACE中.AB=AC,AD=AE,如果由“SAS”可以判定△ABD≌△ACE,则需补充条件( )
A.∠EAD=∠BAC B.∠B=∠C C.∠D=∠E D.∠EAB=∠CAD
【解答】解:补充∠EAD=∠BAC,
∵∠EAD=∠BAC,
∴∠EAD+∠DAC=∠BAC+∠DAC,
即∠EAC=∠DAB,
在△AEC和△ADB中M
,
∴△ABD≌△ACE(SAS).
故选:A.
12.如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
【解答】解:∵AB=AC,∠A=∠A,
∴若以“SAS”得出△ABE≌△ACD,
则AE=AD.
故选:C.
13.把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
【解答】解:∵∠CEA=∠ADB=∠CAB=90°,
∴∠ECA+∠EAC=∠EAC+∠DAB=∠DAB+∠DBA=90°,
∠ECA=∠DAB,∠EAC=∠DBA,
又AC=AB,
∴△AEC≌△BAD,
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE=3+5=8.
故选:C.
14.下面条件中,不能证出Rt△ABC≌Rt△A'B'C'的是( )
A.AC=A'C',BC=B'C' B.AB=A'B',AC=A'C'
C.AB=B'C',AC=A'C' D.∠B=∠B',AB=A'B'
【解答】解:
当AC=A'C',BC=B'C'时,在两三角形中,可利用HL或SAS来证明,故A可以;
当AB=A'B',AC=A'C'时,在两三角形中,可利用HL或SAS来证明,故B可以;
当AB=B'C',AC=A'C'时,AB和B′C不是对应边,故不能证明两三角形全等,故C不可以;
当∠B=∠B′,AB=A′B′时,在两三角形中,可用AAS或ASA来证明,故D可以;
故选:C.
15.如图,在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法:
①AD平分∠EDF;
②△EBD≌△FCD;
③AD⊥BC;
④BD=CD.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵AB=AC,AD是角平分线,
∴BD=CD,AD⊥BC,
又∵BE=CF,
∴△EBD≌△FCD,且△ADE≌△ADF,
∴∠ADE=∠ADF,即AD平分∠EDF.
所以四个都正确.
故选:D.
16.已知:如图,在等边三角形ABC,AD=BE=CF,D,E,F不是各边的中点,AE,BF,CD分别交于P,M,N在每一组全等三角形中,有三个三角形全等,在图中全等三角形的组数是( )
A.5 B.4 C.3 D.2
【解答】解:∵△ABC是等边三角形
∴∠A=∠B=∠C,AC=AB=BC
∵AD=BE=CF
∴△CFB≌△BEA≌△ADC;
∵AD=BE=CF
∴AF=BD=CE
∵∠A=∠B=∠C,AC=AB=BC
∴△CAE≌△BAF≌△AEC;
∵∠EAB=∠DCA=∠CFB(△CFB≌△BEA≌△ADC)
∴∠CAN=∠BPA=∠BCM
∵AC=AB=BC
∴△CMB≌△BPA≌△ANC;
∴CM=BP=AN
∵AD=BE=CF,∠EAB=∠DCA=∠CFB
∴△CFM≌△BEP≌△ADN;
∵AE=BF=CD,CM=BP=AN
∴AP=BM=CN
∵AF=BD=CE,∠FAP=∠MBD=∠ECN
∴△AFP≌△BMD≌△CNE.
故选:A.
二.填空题(共11小题)
17.如图,Rt△ABC和Rt△DEF,∠C=∠F=90°
(1)若∠A=∠D,BC=EF,则Rt△ABC≌Rt△DEF的依据是 AAS .
(2)若∠A=∠D,AC=DF,则Rt△ABC≌Rt△DEF的依据是 ASA .
(3)若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF的依据是 AAS .
(4)若AC=DF,AB=DE,则Rt△ABC≌Rt△DEF的依据是 HL .
(5)若AC=DF,CB=FE,则Rt△ABC≌Rt△DEF的依据是 SAS .
【解答】解:(1)若∠A=∠D,BC=EF,又因为∠C=∠F=90°,所以可根据AAS判定Rt△ABC≌Rt△DEF;
(2)若∠A=∠D,AC=DF,又因为∠C=∠F=90°,所以可根据ASA判定Rt△ABC≌Rt△DEF;
(3)若∠A=∠D,AB=DE,又因为∠C=∠F=90°,所以可根据AAS判定Rt△ABC≌Rt△DEF;
(4)因为∠C=∠F=90°,若AC=DF,AB=DE,所以可根据HL判定Rt△ABC≌Rt△DEF;
(5)若AC=DF,CB=FE,又因为∠C=∠F=90°,所以可根据SAS判定Rt△ABC≌Rt△DEF.
故答案为AAS、ASA、AAS、HL、SAS.
18.已知:如图,∠1=∠3,∠2=∠4,则△ ABC ≌△ CDA .
【解答】解:∵在△ABC和△CDA中,
∴△ABC≌△CDA(ASA),
故答案为:ABC;CDA.
19.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需增加的条件是 AE=DC .
【解答】解:条件是AE=DC,
理由是:在△ABE和△DBC中,
,
∴△ABE≌△DBC(SSS),
故答案为:AE=DC.
20.已知:如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△ ABE ≌△ DCF (HL).
【解答】证明:∵在△ABE和△DCF中,
AE⊥BC,DF⊥BC,AE=DF,AB=DC,
符合直角三角形全等条件HL,
所以△ABE≌△DCF,
故填:ABE;DCF.
21.△ABC和△FED中,BE=FC,∠A=∠D.当添加条件 ∠B=∠DEC 时(只需填写一个你认为正确的条件),就可得到△ABC≌△DFE,依据是 AAS .
【解答】解:添加∠B=∠DEC.
∵BE=FC,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
故答案为:∠B=∠DEC,AAS
22.判定两直角三角形全等的各种条件:(1)一锐角和一边对应相等(2)两边对应相等(3)两锐角对应相等.其中能得到两个直角三角形全等的条件是 (1)和(2) .
【解答】解:∵(1)一锐角与一边对应相等,
可利用AAS或ASA判定两直角三角形全等,
(2)两边对应相等,可利用HL或ASA判定两直角三角形全等;
(3)两锐角对应相等,缺少对应边相等这一条件,
所以不能判定两直角三角形全等.
故(1)和(2).
23.如图,AD=AE,BE=CD,∠1=∠2,∠C=50°,那么∠B= 50 度.
【解答】解:∵AD=AE,∠1=∠2,AF=AF,
∴△ADF≌△AEF(SAS),
∴DF=EF,
又BE=CD,
∴BF=CF,
又∠DFB=∠EFC,
∴△DFB≌△EFC,
∠B=∠C,
∵∠C=50°,
∴∠B=50°.
故填50.
24.如图,已知∠1=∠2,AB⊥AC,BD⊥DC,AC、BD相交于点E,则图中的全等三角形有 2 对.
【解答】解:∵AB⊥AC,BD⊥DC,
∴∠A=∠D=90°,
在△ACB和△DBC中,
,
∴△ABC≌△DCB(AAS),
∴AB=DC,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
故答案为:2.
25.如图,在△ABC中,AB=AC,BE=CD,BD=CF,若∠B=50°,则∠EDF的度数为 50 度.
【解答】解:∵在△ABC中,AB=AC
∴∠B=∠C
∵BE=CD,BD=CF
∴△BED≌△CDF(SAS)
∴∠BDE=∠CFD,∠BED=∠CDF
∵∠EDF=180°﹣∠CDF﹣∠BDE=180°﹣(∠CDF+∠BDE)
∵∠B=50°
∴∠BDE+∠BED=130°即∠CDF+∠BDE=130°
∴∠EDF=50°.
故填50.
26.有一锐角和斜边对应相等的两个直角三角形 全等 ,理由是 AAS .
【解答】解:根据直角三角形的性质,有一锐角和斜边对应相等,且两直角相等,由AAS可判定两三角形全等.
27.如图,已知在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE,垂足分别是D、E,若CE=3,BD=7,则DE= 4 .
【解答】解:∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°
∵∠BAC=90°,
∴∠BAD=∠BAC﹣∠CAE=90°﹣∠CAE,
在△AEC中,∠ACE=∠AEC﹣∠CAE=90°﹣∠CAE,
∴∠BAD=∠ACE,
在△ADB和△CEA中,AB=AC
∴△ADB≌△CEA(AAS),
∴CE=AD,BD=AE,
∴DE=AE﹣AD=BD﹣CE=7﹣3=4.
故填空答案:4.
三.解答题(共11小题)
28.如图,在△ABC和△DEF中,B,E,C,F在同一条直线上.下面给出四个论断:
①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF.
任选三个作为已知条件,余下一个作为结论,可得到几个命题?其中真命题有几个?分别给出证明.
【解答】解:(1)①③④为条件,②为结论;
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DF;故本命题为真命题;
(2)①②④为条件,③为结论;
∵BE=CF,∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ABC=∠DEF;故本命题为真命题;
(3)①②③为条件,④为结论;
无法证明△ABC≌△DEF,故本命题不是真命题;
(4)②③④为条件,①为结论;
无法证明△ABC≌△DEF,故本命题不是真命题;
答:可得到4个命题,其中真命题有2个.
29.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是?(只需写一个,不添加辅助线)
【解答】解:AC=DF,
理由是:∵BF=CE,
∴BF+FC=CE+CF,
∴BC=EF,
∵AC∥DF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
即这个条件可以是AC=DF.
30.如图,已知△ABC中,∠BAC=90°,AB=AC,点P为BC边上一动点(BP<CP),分别过B、C作BE⊥AP于E,CF⊥AP于F.
(1)求证:EF=CF﹣BE.
(2)若点P为BC延长线上一点,其它条件不变,则线段BE、CF、EF是否存在某种确定的数量关系?画图并直接写出你的结论.
【解答】解:(1)证明:∵BE⊥AP,CF⊥AP,
∴∠AEB=∠AFC=90°.
∴∠FAC+∠ACF=90°,
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中,
,
∴△ABE≌△CAF(AAS),
∴AE=CF,BE=AF.
∵EF=AE﹣AF,
∴EF=CF﹣BE;
(2)EF=BE+CF
理由:∵BE⊥AP,CF⊥AP,
∴∠AEB=∠AFC=90°.
∴∠FAC+∠ACF=90°,
∵∠BAC=90°,
∴∠BAE+∠FAC=90°,
∴∠BAE=∠ACF.
在△ABE和△CAF中,
,
∴△ABE≌△CAF(AAS),
∴AE=CF,BE=AF.
∵EF=AE+AF,
∴EF=BE+CF.
31.如图,在△ABC中,∠C=90゜,D是AB上一点,DM⊥AB,且DM=AC,过M作ME∥BC交AB于E.求证:ME=AB.
【解答】证明:∵ME∥BC,
∴∠B=∠MED,
在△DME和△CAB中
,
∴△DME≌△CAB (AAS),
∴ME=AB.
32.如图,点A,C,B,D在同一条直线上,AC=BD,AM=CN,BM=DN,求证:AM∥CN,BM∥DN.
【解答】证明:∵AC=BD,
∴AC+BC=BD+BC,即AB=CD,
∵在△ABM和△CDN中,
,
∴△ABM≌△CDN(SSS),
∴∠A=∠NCD,∠MBA=∠D,
∴AM∥CN,BM∥DN.
33.已知:如图,AD是△ABC的高,E是AD上一点.AD=BD,DE=DC,
求证:(1)∠1=∠C.(2)BE⊥AC.
【解答】证明:(1)∵AD⊥BC于点D,
∴∠ADB=∠ADC=90°,
∵AD=BD,DE=DC,
在Rt△BDE和Rt△ADC中,
∵,
∴△BDE≌△ADC,
∴∠1=∠C;
(2)先延长BE交AC上一点F,
∵△BDE≌△ADC,
∴∠DBE=∠CAD,
∵∠CAD+∠C=90°,
∴∠CBF+∠C=90°,
∴∠BFC=90°
∴BF⊥AC,
∴BE⊥AC.
34.已知:如图,AD∥BC,∠B=∠D.求证:△ADC≌△CBA.
【解答】解:∵AD∥BC,
∴∠ACB=∠DAC,
在△ADC与△CBA中,
,
∴△ADC≌△CBA(AAS).
35.已知:如图所示,E是AB延长线上的一点,AE=AC,AD平分∠BAC交BC于点D,BD=BE.
求证:∠ABC=2∠C.
【解答】证明:∵AD平分∠BAC,
∴∠1=∠2,
在△ADE和△ADC中,
∵AE=AC,∠1=∠2,AD=AD,
∴△ADE≌△ADC,
∴∠E=∠C,
∵BE=BD,
∴∠E=∠BDE,
∴∠ABC=∠E+∠BDE=2∠E,
∴∠ABC=2∠C.
36.已知:如图,M是AB的中点,MC=MD,∠1=∠2
证明:AC=BD.
【解答】证明:∵M是AB中点,
∴MA=MB,
在△AMC和△BMD中,
,
∴△AMC≌△BMD,
∴AC=BD.
37.已知,如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,请说明AC=AB+BD.
方法一:截长法:(图2)
在较长的线段上截一条线段等于较短线段.
方法二:补短法:(图3)
延长较短线段和较长线段相等.
【解答】解:方法一、在AC上截取AE=AB,连接DE,
∵AD是△ABC的角平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中
∴△BAD≌△EAD,
∴BD=DE,∠B=∠AED,
∵∠B=2∠C,∠AED=∠C+∠EDC,
∴∠C=∠EDC,
∴DE=EC=BD,
∴AC=AE+CE=AB+BD;
方法二、如图3,延长AB到F,使AF=AC,连接DF,
∵在△FAD和△CAD中
∴△FAD≌△CAD,
∴∠C=∠F,
∵∠ABC=2∠C,∠ABC=∠F+∠BDF,
∴∠F=∠BDF,
∴BD=BF,
∴AC=AF=AB+BD.
38.如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC.
求证:OB=OC.
【解答】证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠BDC=∠AEB=∠CEB=90°.
∵AO平分∠BAC,
∴∠1=∠2.
在△AOD和△AOE中,,
∴△AOD≌△AOE(AAS).
∴OD=OE.
在△BOD和△COE中,,
∴△BOD≌△COE(ASA).
∴OB=OC.
