2018-2019学年八年级数学上册13.4课题学习最短路径问题同步作业设计含答案
文档属性
| 名称 | 2018-2019学年八年级数学上册13.4课题学习最短路径问题同步作业设计含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 129.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-29 13:57:12 | ||
图片预览


文档简介
13.4 课题学习 最短路径问题
一、选择题
1. 如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若
AE=2,当EF+CF取得最小值时,则∠ECF的度数为( ).
(第1题图)
A. 15° B. 22.5° C. 30° D. 45°
2. 如图,∠AOB=30°,内有一点P且OP=,若M、N为边OA、OB上两动点,那么△PMN的周长最小为( ).
(第2题图)
A. B. 6 C. D.
3. 已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若
△PEF的周长的最小值等于2,则α=( ).
(第3题图)
A. 30° B. 45° C. 60° D. 90°
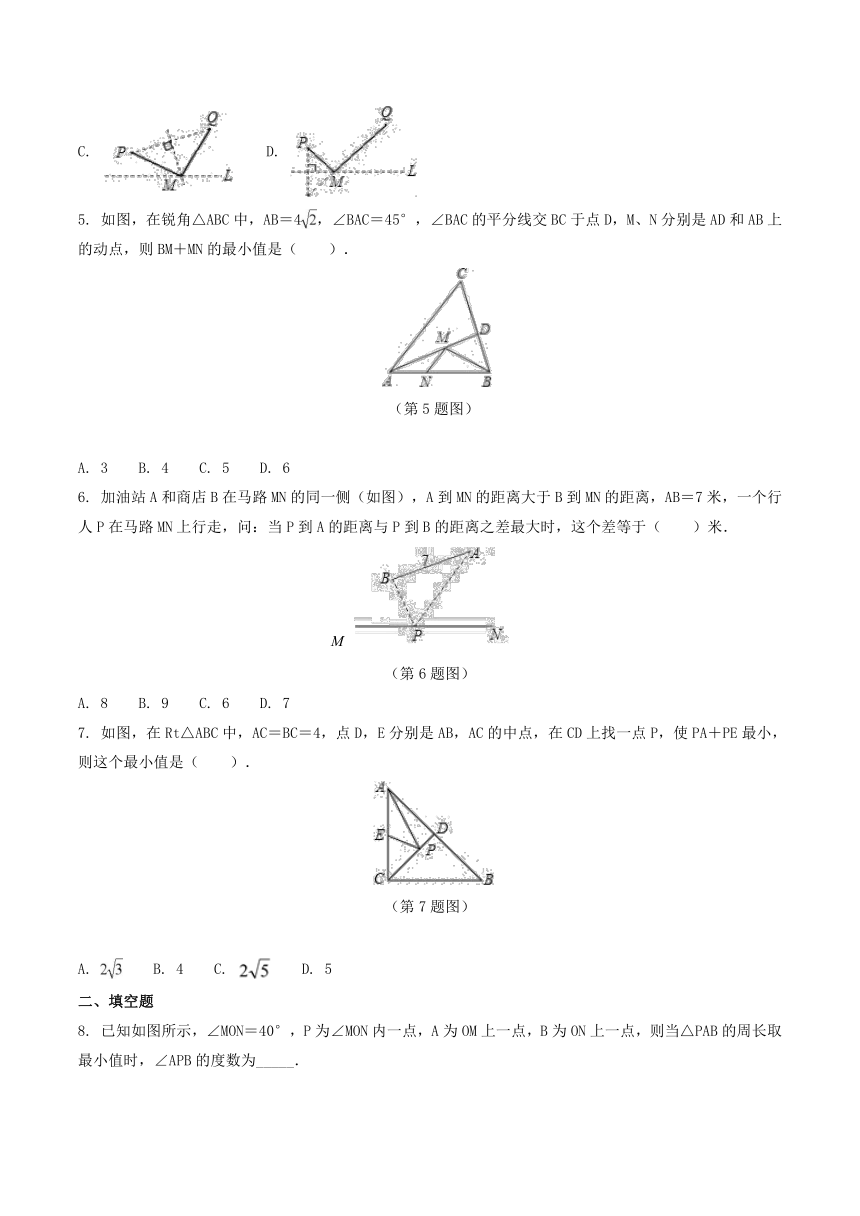
4. 直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).
A. B.
C. D.
5. 如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ).
(第5题图)
A. 3 B. 4 C. 5 D. 6
6. 加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7米,一个行人P在马路MN上行走,问:当P到A的距离与P到B的距离之差最大时,这个差等于( )米.
(第6题图)
A. 8 B. 9 C. 6 D. 7
7. 如图,在Rt△ABC中,AC=BC=4,点D,E分别是AB,AC的中点,在CD上找一点P,使PA+PE最小,则这个最小值是( ).
(第7题图)
A. B. 4 C. D. 5
二、填空题
8. 已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为_____.
(第8题图)
9.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为 .
(第9题图)
10.如图所示:∠AOB的内部有一点P,到顶点O的距离为5cm,M、N分别是射线OA、OB上的动点.若∠AOB=30°,则△PMN的周长的最小值为 .
(第10题图)
三、解答题
11. 已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
(第11题图)
12. 某大型农场拟在公路L旁修建一个农产品储藏、加工厂,将该农场两个规模相同的水果生产基地A、B的水果集中进行储藏和技术加工,以提高经济效益.请你在图中标明加工厂所在的位置C,使A、B两地到加工厂C的运输路程之和最短.(要求:用尺规作图,保留作图痕迹,不写作法和证明)
(第12题图)
13. 如图,△ABC的边AB、AC上分别有定点M、N,请在BC边上找一点P,使得△PMN的周长最短. (写出作法,保留作图痕迹)
(第13题图)
14. 在某一地方,有条小河和草地,一天某牧民的计划是从A处的牧场牵着一只马到草地牧马,再到小河饮马,你能为他设计一条最短的路线吗?(在N上任意一点即可牧马,M上任意一点即可饮马.)(保留作图痕迹,需要证明)
(第14题图)
参考答案
1.C 2.D 3.A 4.D 5.B 6.D 7.C
100° 分析:如图,作出P点关于OM,ON的对称点P1,P2交OM,ON于A,B两点,此时△PAB的周长最小,根据题意可知: ∠P1PP2=180°-∠MON=180°-40°=140,所以∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,所以∠APB=140°-40°=100°.
(第8题答图)
5 分析:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N.∵BD平分∠ABC,ME⊥AB于点E,MN⊥BC于N,∴MN=ME,∴CE=CM+ME=CM+MN的最小值.∵三角形ABC的面积为10,AB=4,∴×4?CE=10,∴CE==5.即CM+MN的最小值为5.
(第9题答图)
10. 5 cm 分析:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.∵点P关于OA的对称点为C,关于OB的对称点为D,∴PM=CM,OP=OC,∠COA=∠POA.∵点P关于OB的对称点为D,∴PN=DN,OP=OD,∠DOB=∠POB,∴OC=OD=OP=5cm,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,∴△COD是等边三角形,∴CD=OC=OD=5cm.∴△PMN的周长的最小值为PM+MN+PN=CM+MN+DN≥CD=5cm.
(第10题答图)
11.解:(1)如图所示.
画法:①作点M关于射线OP的对称点M';
②连接M'N交OP于点A;
③作点N关于射线OQ的对称点N';
④连接N'M交OQ于点B.
(2)AM+AN与BM+BN的大小关系是:AM+AN=BM+BN.
(第11题答图)
12.解:作点A关于直线l的对称点E,连接BE.根据对称的性质可知,BE的长即为AC+BC的最短距离,BE与直线l的交点C即是所求的点.如图,
(第12题答图)
13.解:作点N关于BC的对称点N′,连接MN′交BC于点P,由两点之间线段最短可知P点即为所求点.
14.证明:作点A关于草地所在直线的对称点E,作点B关于小河所在直线的对称点F,连接EF,交河流所在直线于点D,交草地所在直线于点C,连接AC,CD,DB,根据轴对称性质,AC+CD+DB的最小值即为EF的长.在ON上任意取一点T,在OM上任意取一点R,连接FR,BR,RT,ET,AT,
∵A,E关于ON对称,∴AC=EC.
同理BD=FD,FR=BR,AT=ET,
∴AC+CD+DB=EC+CD+FD=EF,AT+TR+BR=ET+TR+FR.
∵ET+TR+FR>EF,∴AC+CD+DB<AT+TR+BR,即沿AC-CD-DB路线走是最短的路线,
(第14题图)
M
PAGE
一、选择题
1. 如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若
AE=2,当EF+CF取得最小值时,则∠ECF的度数为( ).
(第1题图)
A. 15° B. 22.5° C. 30° D. 45°
2. 如图,∠AOB=30°,内有一点P且OP=,若M、N为边OA、OB上两动点,那么△PMN的周长最小为( ).
(第2题图)
A. B. 6 C. D.
3. 已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若
△PEF的周长的最小值等于2,则α=( ).
(第3题图)
A. 30° B. 45° C. 60° D. 90°
4. 直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).
A. B.
C. D.
5. 如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ).
(第5题图)
A. 3 B. 4 C. 5 D. 6
6. 加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7米,一个行人P在马路MN上行走,问:当P到A的距离与P到B的距离之差最大时,这个差等于( )米.
(第6题图)
A. 8 B. 9 C. 6 D. 7
7. 如图,在Rt△ABC中,AC=BC=4,点D,E分别是AB,AC的中点,在CD上找一点P,使PA+PE最小,则这个最小值是( ).
(第7题图)
A. B. 4 C. D. 5
二、填空题
8. 已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为_____.
(第8题图)
9.如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为 .
(第9题图)
10.如图所示:∠AOB的内部有一点P,到顶点O的距离为5cm,M、N分别是射线OA、OB上的动点.若∠AOB=30°,则△PMN的周长的最小值为 .
(第10题图)
三、解答题
11. 已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
(第11题图)
12. 某大型农场拟在公路L旁修建一个农产品储藏、加工厂,将该农场两个规模相同的水果生产基地A、B的水果集中进行储藏和技术加工,以提高经济效益.请你在图中标明加工厂所在的位置C,使A、B两地到加工厂C的运输路程之和最短.(要求:用尺规作图,保留作图痕迹,不写作法和证明)
(第12题图)
13. 如图,△ABC的边AB、AC上分别有定点M、N,请在BC边上找一点P,使得△PMN的周长最短. (写出作法,保留作图痕迹)
(第13题图)
14. 在某一地方,有条小河和草地,一天某牧民的计划是从A处的牧场牵着一只马到草地牧马,再到小河饮马,你能为他设计一条最短的路线吗?(在N上任意一点即可牧马,M上任意一点即可饮马.)(保留作图痕迹,需要证明)
(第14题图)
参考答案
1.C 2.D 3.A 4.D 5.B 6.D 7.C
100° 分析:如图,作出P点关于OM,ON的对称点P1,P2交OM,ON于A,B两点,此时△PAB的周长最小,根据题意可知: ∠P1PP2=180°-∠MON=180°-40°=140,所以∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,所以∠APB=140°-40°=100°.
(第8题答图)
5 分析:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N.∵BD平分∠ABC,ME⊥AB于点E,MN⊥BC于N,∴MN=ME,∴CE=CM+ME=CM+MN的最小值.∵三角形ABC的面积为10,AB=4,∴×4?CE=10,∴CE==5.即CM+MN的最小值为5.
(第9题答图)
10. 5 cm 分析:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.∵点P关于OA的对称点为C,关于OB的对称点为D,∴PM=CM,OP=OC,∠COA=∠POA.∵点P关于OB的对称点为D,∴PN=DN,OP=OD,∠DOB=∠POB,∴OC=OD=OP=5cm,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,∴△COD是等边三角形,∴CD=OC=OD=5cm.∴△PMN的周长的最小值为PM+MN+PN=CM+MN+DN≥CD=5cm.
(第10题答图)
11.解:(1)如图所示.
画法:①作点M关于射线OP的对称点M';
②连接M'N交OP于点A;
③作点N关于射线OQ的对称点N';
④连接N'M交OQ于点B.
(2)AM+AN与BM+BN的大小关系是:AM+AN=BM+BN.
(第11题答图)
12.解:作点A关于直线l的对称点E,连接BE.根据对称的性质可知,BE的长即为AC+BC的最短距离,BE与直线l的交点C即是所求的点.如图,
(第12题答图)
13.解:作点N关于BC的对称点N′,连接MN′交BC于点P,由两点之间线段最短可知P点即为所求点.
14.证明:作点A关于草地所在直线的对称点E,作点B关于小河所在直线的对称点F,连接EF,交河流所在直线于点D,交草地所在直线于点C,连接AC,CD,DB,根据轴对称性质,AC+CD+DB的最小值即为EF的长.在ON上任意取一点T,在OM上任意取一点R,连接FR,BR,RT,ET,AT,
∵A,E关于ON对称,∴AC=EC.
同理BD=FD,FR=BR,AT=ET,
∴AC+CD+DB=EC+CD+FD=EF,AT+TR+BR=ET+TR+FR.
∵ET+TR+FR>EF,∴AC+CD+DB<AT+TR+BR,即沿AC-CD-DB路线走是最短的路线,
(第14题图)
M
PAGE
