苏科版九年级物理上册 第十一章 简单机械和功 讲义练习(含答案)
文档属性
| 名称 | 苏科版九年级物理上册 第十一章 简单机械和功 讲义练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 616.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-09-30 22:18:05 | ||
图片预览




文档简介
课 题 第十一章 简单机械和功
一、杠杆 1.杠杆:一根在力的作用下能绕着固定点转动的硬棒就是杠杆。杠杆的五要素是:支点、动力、阻力、动力臂和阻力臂,杠杆可以是直的硬棒,如撬棒等;也可以是弯的,如羊角锤。 2.杠杆的五要素: (1)支点:杠杆绕着转动的点,即图中的O点. (2)动力:使杠杆转动的力,即图中的F1。 (3)阻力:阻碍杠杆转动的力,即图中的F2。 (4)动力臂:从支点到动力作用线的距离,即图中的。 (5)阻力臂:从支点到阻力作用线的距离,,即图中的。 3.杠杆的平衡条件是:动力×动力臂=阻力×阻力臂,用字母表示为:;杠杆的平衡不是单独由力或力臂决定的,而是由它们的乘积来决定的。 4.杠杆分类:
(1)省力杠杆:>,F1<F2。
这类杠杆的特点是动力臂大于阻力臂,平衡时动力F1小于阻力F2,即用较小的动力就可以克服较大的阻力。但是实际工作是动力移动的距离却比阻力移动的距离大,即要费距离。如撬起重物的撬棒,开启瓶盖的起子、铡草用的铡刀等,都属于这一类杠杆。
(2)费力杠杆:<,F1>F2。
这类杠杆的特点是动力臂小于阻力臂,平衡时动力F1大于阻力F2,即要用较大的动力才能克服阻力完成工作,但它的优点是杠杆工作时,动力移动较小的距离就能使阻力移动较大的距离。使工作方便,也就是省了距离。如缝纫机踏板、挖土的铁锨、大扫帚、夹煤块的火钳,这些杠杆都是费力杠杆。
(3)等臂杠杆:=,F1=F2。
这类杠杆的动力臂等于阻力臂,平衡时动力F1等于阻力F2,工作时既不省力也不费力,如天平、定滑轮就是等臂杠杆。 注: 1.力臂的画法: (1)明确支点,用O表示 ; (2)通过力的作用点沿力的方向画一条直线; (3)过支点O作该力的作用线的垂线; (4)用两头带箭头的线段标示出支点到力的作用线的垂线段,写上相应的字母(或)。
2.杠杆的平衡:杠杆在力的作用下保持静止或匀速转动,杠杆就处于平衡状态。
3.杠杆的平衡条件也称为杠杆的原理,最早是由古希腊学者阿基米德总结出来的。 二、滑轮 1.定滑轮: (1)定义:工作时,轴的位置固定不动的滑轮,称为定滑轮。 (2)实质:如图甲所示,我们可把一条直径看成杠杆,圆心就是杠杆的支点,因此,定滑轮实质是等臂杠杆。 (3)作用:不能省力,但可以改变用力方向。 2.动滑轮: (1)定义:轴的位置随被拉动的物体一起运动的滑轮,称为动滑轮。 (2)实质:如图乙所示,它实质是动力臂为阻力臂2倍的省力杠杆,它的转动轴是阻力作用点。 (3)作用:可以省力,但是不能改变力的方向。 3.滑轮组: (1)组成:定滑轮和动滑轮 (2)作用:既可以改变力的大小又可以改变力的方向 (3)滑轮组绳子自由端的拉力:(忽略绳子重和摩擦)。 (4)物体上升的高度h与绳子自由端移动的距离s的关系:。 注: 1. 组装滑轮组,在知道或算出滑轮组承担重物的绳子段数情况下,根据“奇动偶定”的原则,先确定绳子的一端是挂在动滑轮或定滑轮的钩上,再由里向外顺次绕线。 2.时间t内,物体上升高度h,绳子自由端移动的距离s;物体移动的速度,绳子自由端移动的速度;所以物体上升的速度与绳子自由端移动的速度关系:。 三、功 1.做功的两个必要因素:
(1)作用在物体上的力;
(2)物体在力的方向上通过的距离。
2.不做功的三种情况
(1)物体受力,但物体没有在力的方向上通过距离。此情况叫“劳而无功”。
(2)物体移动了一段距离,但在此运动方向上没有受到力的作用(如物体因惯性而运动)。此情况叫“不劳无功”。
(3)物体既受到力,又通过一段距离,但两者方向互相垂直(如起重机吊起货物在空中沿水平方向移动)。此情况叫“垂直无功”。 3.功的计算:
(1)公式:一般式 W=Fs ;常用式 W=Gh(克服重力做功)或W=f阻s(克服摩擦阻力做功)。
(2)单位:焦耳(J) 4.注意事项: (1)F与s的方向应在同一直线上(初中要求)(比如一个人提着一重物G,从山脚顺着“之”字形的山路爬到山顶,此时人克服重力做功所移动的距离并不是山路的长,而是从山脚到山顶的高)
(2)做功的多少,由W=Fs决定,而与物体的运动形式无关。
注: 1.判断物体做功的依据:做功的两个必要因素,重点抓住力作用在物体上是否有“成效”。 2.在分析做功情况时还应注意以下几点:
(1)当物体的受力方向与运动方向不垂直时,这个力就要做功。
(2)一个物体同时受几个力的作用时,有一些力做了功,有些力没有做功。因此,讲做功必须指出是哪一个力对哪一个物体做功。
(3)什么叫物体克服阻力做功:若物体在运动方向上受到一个与此方向相反的力F的作用,我们通常说物体克服阻力F做了功。
比如:物体在竖直向上运动h的过程中,物体克服重力做功,功的大小为W=Gh; 再如:物体在水平方向上向前运动s,物体克服摩擦力做功,功的大小为W=fs。 四、功率
1.物理意义:表示物体做功的快慢。 2.定义:物体在单位时间内所做的功。 3.计算式:, P 表示功率,W 表示功,t 表示时间,使用公式计算功率时,必须注意W 和t的对应关系。W 为在t时间内所做的功,而t为做W 这么多的功所用的时间。 4.推导式:,式中F为做功的力而v为速度。 5.单位:瓦(W) 注: 1.注意区别功与功率。功率与功是两个不同的物理量,“功”表示做功的“多少”,而“功率”则表示做功的“快慢”,“多少”与“快慢”的意义不一样。只有在做功时间相同时,做功多的就做功快。否则,做功多,不一定做功就快,即“功率”不一定就大。也就是说:功率与功和时间两个因素有关。
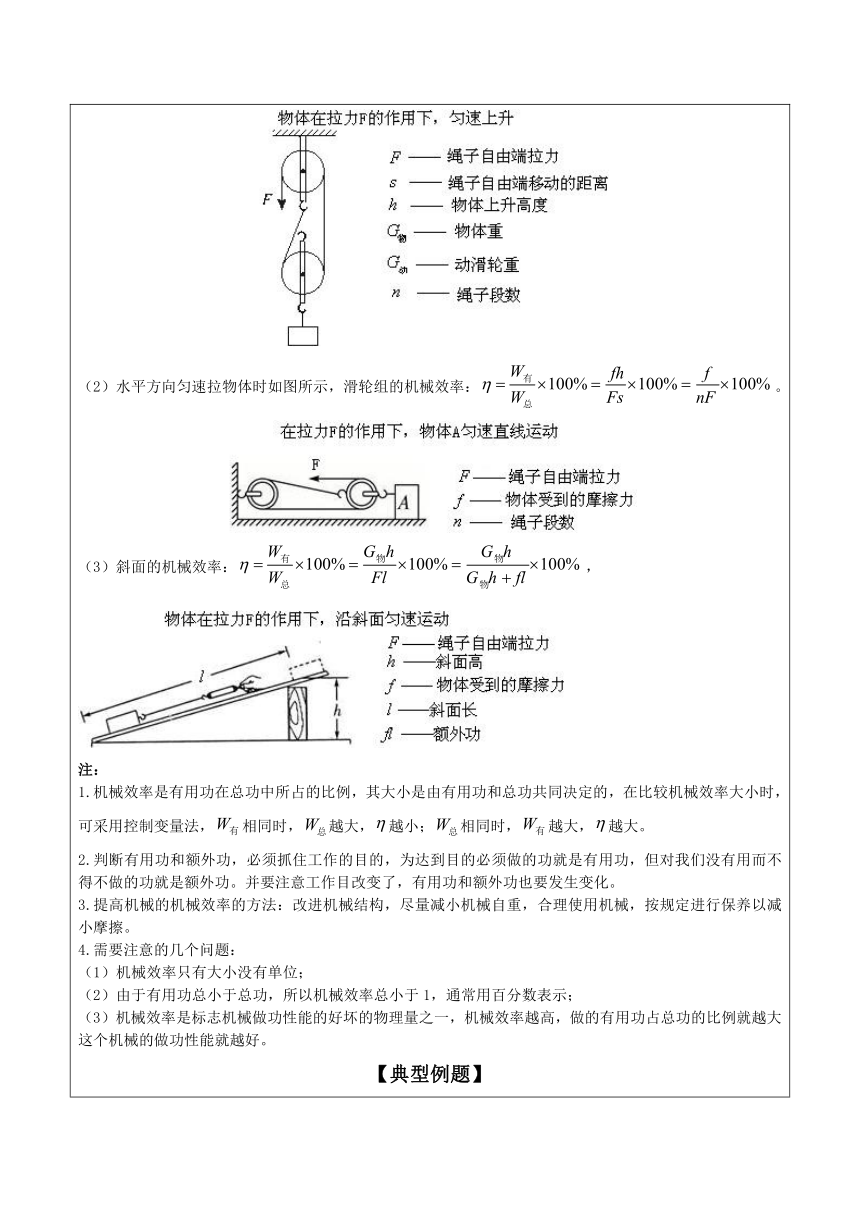
2.由P=W/t变形为P=Fv可知:功率一定时,力F与速度v成反比。 五、机械效率 1.机械效率:有用功与总功的比值叫作机械效率。 2. 公式为: 3.推导式: (1)竖直方向匀速提升物体时,滑轮组的机械效率:, 忽略绳重和摩擦,绳子自由端的拉力:, 滑轮组的机械效率:。 (2)水平方向匀速拉物体时如图所示,滑轮组的机械效率:。 (3)斜面的机械效率:, 注:? 1.机械效率是有用功在总功中所占的比例,其大小是由有用功和总功共同决定的,在比较机械效率大小时,可采用控制变量法,相同时,越大,越小;相同时,越大,越大。 2.判断有用功和额外功,必须抓住工作的目的,为达到目的必须做的功就是有用功,但对我们没有用而不得不做的功就是额外功。并要注意工作目改变了,有用功和额外功也要发生变化。 3.提高机械的机械效率的方法:改进机械结构,尽量减小机械自重,合理使用机械,按规定进行保养以减小摩擦。 4.需要注意的几个问题: (1)机械效率只有大小没有单位; (2)由于有用功总小于总功,所以机械效率总小于1,通常用百分数表示; (3)机械效率是标志机械做功性能的好坏的物理量之一,机械效率越高,做的有用功占总功的比例就越大这个机械的做功性能就越好。 【典型例题】 例1.如图所示在用羊角锤拔钉子时,若O为支点,画出在A点施加的最小力F的示意图及其力臂L。 【答案与解析】1.确定杠杆中的支点和动力作用点的位置;2.连接支点与动力作用点,即连接AO,得到最长的线段;3.经过动力作用点做出与该线段垂直的直线。 例2.如图所示,唐师傅想用最省力的方法把一个油桶推上台阶,请你在图中画出这个力的示意图。 【答案与解析】在处理此类杠杆中最小力的问题时,可按以下步骤进行:①确定支点和动力作用点;
②过动力作用点做出与动力臂垂直的直线,即动力作用线。 例3.假期里明明和他爸爸、妈妈一起参加了一个家庭游戏活动。活动的要求是:家庭成员中的任意两名成员分别站在如图所示的木板上,恰好使木板水平平衡。
(1)若明明和爸爸的体重分别为350N和700N,明明站在左侧离中央支点3m处,明明的爸爸应站在哪一侧?应离中央支点多远才能使木板水平平衡?
(2)若明明和他爸爸已经成功地站在了木板上,现在他们同时开始匀速相向行走,明明的速度是0.4m/s,爸爸的速度是多大才能使木板水平平衡不被破坏? 【答案与解析】(1)明明和爸爸对杠杆施加的力分别为F1=350N,F2=700N,F1的力臂L1=3m,
根据杠杆平衡条件:F1L1=F2L2, 即:350N×3m=700N×L2, 所以,L2=1.5m, 答:爸爸站在距离支点1.5m的另一侧。 (2)设:明明和爸爸匀速行走的速度分别为v1和v2, 行走时间为t,要保证杠杆水平平衡, 则有F1(L1-v1t)=F2(L2-v2t) 350N(3m-0.4m/s×t)=700N(1.5m-v2t) 解得:v2=0.2m/s。 答:明明和爸爸匀速相向行走,明明的速度是0.4m/s,爸爸的速度是0.2m/s才能使木板水平平衡不被破坏。 例4.如图所示,一个厚度均匀的薄木板长2m,木块右端用一根绳子悬挂。绳子所能承受的最大拉力为10N。一个大小不计的木块重40N,它从木块左边的O点开始以0.2m/s的速度向木板右端匀速移动,求:木块运动多长时间绳子断裂?(木板重力不计)。 【答案与解析】根据杠杆的平衡条件:,可得:; 由公式,可得:。 答:木块运动2.5s后绳子断裂。 例5.如图所示,重为500N的某人站在重为350N的木板上,木板成水平状态,整个装置在空中保持静止,每个滑轮自重为50N,不计摩擦和绳重,则人对木板的压力大小为 N。 【答案】300 【解析】方法一:(1)对人、板、滑轮1受力分析图1:,可得:F=450N; (2)对滑轮1受力分析图2:,可得:; (3)对人受力分析图3:,可得:; 因为人受到的支持力和人对板的压力是一对相互作用力大小相等,所以人对板的压力是300N。 方法二:人的重力500N+木板的重力350N+下面的滑轮的重力50N=900N,读图可知,这900N都由最上面的滑轮承担,而且左右拉力相等。因此,上面滑轮右侧的拉力为450N,减去下面滑轮的自重50N,等于400N.这400N又由两段绳子平均分担,因此,人手处的拉力为200N。于是得出,人对木板的压力=人的重力500N-绳子拉人手的力200N=300N。 例6.如图所示,站在小车上的男孩在绳子末端施加50N的水平拉力F,物体M和小车在水平地面上做相向的匀速直线运动,物体M速度为0.2m/s,小车速度为0.3m/s,则地面对物体M的摩擦力为 N,2s后绳子自由端移动的距离为 m。(不计绳重、滑轮重以及绳与滑轮的摩擦) 【答案】150;3 例7.小勇同学利用星期天积极参加社会实践活动,到养老院当义工,在活动中要帮助老人将3壶相同的油从一楼搬到三楼。小勇第一趟将一壶油从一楼提到三楼,用时20s;第二趟将两壶油从一楼提到三楼,用时30s。已知每壶油的质量为5kg,小勇的质量为45kg,每层楼的楼高是3m。(g=10N/kg) (1)第一趟小勇做了多少有用功?小勇做功的总功率是多少? (2)比较小勇两趟做功效率的高低,并说明理由。 【答案与解析】 (1)第一趟做的有用功:; 第一趟做的总功:; 总功的功率:。 (2)第二趟做功效率高。 理由:小勇两次克服自己体重做的额外功不变,第二趟提两壶油增大了有用功,从而增大有用功在总功中的比值,所以第二趟做功效率高; 答:(1)第一趟小勇做了300J的有用功;小勇做功的总功率是150W。(2)第二趟做功效率高。 理由:小勇两次克服自己体重做的额外功不变,第二趟提两壶油增大了有用功,从而增大有用功在总功中的比值,所以第二趟做功效率高。 例8.一辆车开进了泥潭中,司机取来一个动滑轮欲将汽车从泥潭中拉出,如图所示,若司机用750N的拉力在5s内将汽车水平匀速拉动1m,那么司机所做的功是 J,司机做功的功率是 W,若滑轮的机械效率为60%,汽车所受地面的摩擦力是 N。 【答案】1500;300;900 例9.为了将放置在水平地面上、重G=100N的重物提升到高处。小明同学设计了图甲所示的滑轮组装置。当小明用图乙所示随时间变化的竖直向下拉力F拉绳时,重物的速度υ和上升的高度h随时间t变化的关系图象分别如图丙和丁所示.若重物与地面的接触面积S=5×10-2m2,不计摩擦,绳对滑轮的拉力方向均可看成在竖直方向。求: (1)在1~2s内,若重物上升1.25m,拉力F做的功W。 (2)在2~3s内,拉力F的功率P及滑轮组的机械效率η。 (3)若绳子能承受的最大拉力是1500N,小李体重600N,他站在地面向下拉绳子使物体匀速上升,最大能提升多重的物体? 【答案与解析】(1)在1~2s内,拉力F1=50N,重物上升高度h1=1.25m; 拉力F的作用点下降的距离, 拉力做的功:; 绳子自由端的拉力:, 动滑轮的重力为:; (2)由图可知在2~3s内,重物做匀速运动,,拉力,
∵从动滑轮上直接引出的绳子股数(承担物重的绳子股数)n=3, ∴拉力F的作用点下降的速度, 拉力做功功率(总功率):; 滑轮组的机械效率: (3)绳子能承受的最大拉力是1500N,所以物体的最大重力为:; 所以:。
答:(1)在1~2s内,拉力F做的功为187.5J;
(2)在2~3s内,拉力F的功率为300W,滑轮组的机械效率为83.3%;
(3)最大能提升1750N的物体。 例10.如图甲所示的滑轮组。不计绳重和摩擦,物体重G从400N开始逐渐增加,直到绳子被拉断。每次均匀速拉动绳子将物体提升同样的高度。图乙记录了在此过程中滑轮组的机械效率随物体重力的增加而变化的图象。 (1)当滑轮组的机械效率为40%时,绳子的拉力为多大? (2)2个滑轮总重多少? (3)绳子能承受的最大拉力是多少? (4)当滑轮组的机械效率为80%时,物体重多少? 【答案与解析】(1)从甲图中可知,n=4;从乙图中可知,当η=40%时,G=400N, 根据机械效率:,即:。 (2)设两个动滑轮总重G总,则, 即:。 (3)由乙图可知:当物重最大为G′=3200N时,绳子刚好被拉断,则绳子能承受的最大拉力:
。 (4)根据机械效率:,可得:。
答:(1)当滑轮组的机械效率为40%时,绳子的拉力为250N; (2)2个滑轮总重600N; (3)绳子能承受的最大拉力是950N; (4)当滑轮组的机械效率为80%时,物体重2400N。 例11.某同学用如图所示的实验装置测量滑轮组的机械效率,相关数据记录在下表中, (1)实验中,使用滑轮组提升重物时,应竖直向上 拉动弹簧测力计。 (2)第三次实验中,绳端移动的距离为 m,滑轮组的机械效率为 。 (3)分析实验数据发现,同一滑轮组提升重物的重力变大时,滑轮组的机械效率将 (选填“变大”“变小”或“不变”)。 【答案】(1)匀速;(2)0.45m;80%;(3)变大 【解析】(1)实验中应该匀速竖直向上拉动弹簧测力计,以保证拉力大小恒定。 (2)由图示可知,滑轮组承重绳子有效股数n=3, 第3次测量中,弹簧测力计移动的距离s=nh=3×0.15m=0.45m; 滑轮组的机械效率; (3)根据第1次和第2次数据可知,机械效率分别为: ; ; 两次所用滑轮组相同,但第2次物重大于第1次物重,机械效率也大于第1次的机械效率,所以可得使用同一滑轮组,提高物重可以提高滑轮组的机械效率;答案为:(1)匀速;(2)0.45m;80%;(3)变大。 【复习训练】 一、选择 1.当你用手掌托住一只铁球并绕腕关节向上转动时,手就是一个杠杆、球压在掌心上的力是阻力,腕关节是支点,通过前臂中的伸、屈肌的伸、缩产生动力,使托住球的手向上转动(如图)。那么,人体上的这个杠杆应该是( ) A.省力杠杆 B.省距离杠杆 C.既省力又省距离的杠杆 D.既不省力也不省距离的杠杆 2.下列关于功、功率、机械效率的说法正确的是( ) A.做功多的机器机械效率一定高 B.功率小的机器做功慢 C.机械效率高的机器功率一定大 D.功率大的机器做功时间一定短 3. 如图,杠杆在水平位置平衡,若在杠杆两端各取掉相同质量的物体,则( ) A.杠杆左端下降;把支点向左移动,可使杠杆平衡 B.杠杆左端下降;把支点向右移动,可使杠杆平衡 C.杠杆右端下降;把支点向左移动,可使杠杆平衡 D.杠杆右端下降;把支点向右移动,可使杠杆平衡 4.用下图所示的简单机械,使重量同为G的物体都处于静止状态,其中用力最大的是(均不计摩擦)( )
5.如图所示,甲、乙两滑轮组,它们吊起的重物都是G,滑轮重量及摩擦不计,当重物匀速上升时,两滑轮组绳端拉力分别为F甲、F乙,那么F甲:F乙是( ) A. 1:1 B. 2:3 C. 3:2 D. 1:3 6.图中的剪刀剪纸机械效率为80%,这表示( ) A.若作用在剪刀的动力是1N,则阻力是0.8N B.若作用在剪刀的阻力是1N,则动力是0.8N C.若作用在剪刀的动力做功1J,则有0.2J?的功用于剪纸 D.若作用在剪刀的动力做功1J,则有0.8J?的功用于剪纸 7.下列说法中正确的是( ) A.省力的机械不能省功,机械越省力,其机械效率越高 B.做功越快的机械,虽然它做的功不一定多,但是其机械效率是越高的 C.做相同的额外功时,有用功越大的机械效率越高 D.机械效率越低的时候,做功一定是越慢的 8. 一个滑轮组经改进后提高了机械效率,用它把同一物体匀速提升同样的高度,改进后与改进前相比( ) A.有用功减少,总功减少 B.有用功增加,总功增加 C.有用功不变,总功不变 D.有用功不变,总功减少 9.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为W1,机械效率为η1;用乙滑轮所做的总功为W2,机械效率为η2。若不计绳重与摩擦,则( )
A.W1=W2,η1=η2 B.W1=W2,η1<η2 C.W1<W2,η1>η2 D.W1>W2,η1<η2 10.利用如图所示装置将重为100N的物体匀速从斜面的底端拉到顶端.已知斜面的长是5m,高是2m,拉力为F=50N,则该装置的机械效率为( ) A.40% B.50% C.80% D.100% 二、填空 11.如图所示,用固定在墙上的三角支架ABC放置空调室外机。如果A处螺钉松脱,则支架会绕 点倾翻。已知AB长40cm,AC长30cm。室外机的重力为300N,正好处在AB中点处,则A处螺钉的水平拉力为 N(支架重力不计)。为了安全,室外机的位置应尽量 (选填“靠近”或“远离”)墙壁。 12.杠杆在我国古代早就有了许多巧妙的应用,有时人们使用动力臂比阻力臂长的杠杆是为了 ;有时却要使用费力杠杆,那又是为了 。下列工具中①天平、②扳手、③镊子、④羊角锤、⑤裁衣剪刀、⑥瓶盖起子、⑦筷子、⑧钓鱼杆等都是简单机械,其中属于省力杠杆的是 。(填序号) 13.如图所示,某人将重为150N的物体匀速提起,在2s内绳的自由端移动了6m,则重物上升的速度为 m/s,若拉绳的力为60N,则动滑轮重为 N。(不计绳重和摩擦) 14.小童同学用50N的水平推力,使放在水平桌面上重200N的物体做匀速直线运动,若该物体在10s内移动4m,则在此过程中,物体受到的摩擦力是 N,小童做功的功率是 W。 15.如图所示,用平行于斜面的拉力F,将重为2N的物体沿斜面从底端匀速拉至顶端。若不考虑物体与斜面间的摩擦,则拉力F为 N;若斜面的机械效率为80%,则此时拉力F为 N。 16.如图所示,小刚站在高台上通过滑轮组先后竖直向上匀速提升物体A和物体B。假设在拉绳子的过程中,小刚对绳子的拉力与对高台的压力始终在同一直线上,不计绳重和摩擦。已知小刚的质量为50kg,物体A的质量为54kg,物体B的质量为84kg,动滑轮的质量为6kg。当提升物体A时,滑轮组的机械效率为 ,此时小刚对高台的压力是 N;当提升物体B时,小刚拉力做功的功率为180W,则物体B上升的速度为 m/s。(g取10N/Kg) 三、实验探究 17.物理实验小组的同学,利用如图所示的装置,在杠杆支点的两边分别挂上钩码来探究杠杆的平衡条件。
(1)如图甲所示,为使杠杆在水平位置平衡,应将右端的平衡螺母向 (选填“左”或“右”)移动,将杠杆调在水平位置的目的是为了方便测量 。 (2)实验中测得的数据如表所示,表格中漏填的数据为 N。 ?测量序号?动力F1/N?动力臂l1/cm阻力F2/N??阻力臂l2/cm?①?1?20?2?10?②?2?15?1.5?20?③?3?5??15
(3)有的同学按现有方案得出如下结论:“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”。这个结论与杠杆平衡条件不符,原因是实验过程中 (填字母)。 A.没有改变力的大小?????? B.没有改变力的方向 C.没有改变力的作用点???? D.实验次数较少,结论具有偶然性 18.用如图所示装置测量动滑轮的机械效率。实验时,竖直向上的匀速拉动弹簧测力计,使挂在动滑轮下面的钩码缓缓上升。实验数据如下表。 序号动滑轮重G动/N钩码重力G/N钩码上升高度h/m绳的拉力F/N绳端移动距离s/m?机械效率η①0.110.20.60.483.3%②0.120.21.10.4③0.220.21.20.483.3%
(1)第②次实验时,测得动滑轮的机械效率约为 。
(2)分析表中数据可知,对于同一动滑轮,所提升钩码的重力增大,机械效率将 ;提升相同重力的钩码时,动滑轮的重力增大,其机械效率将 。(选填“增大”“减小”或“不变”)
(3)分析表中数据可知,,可能的原因是: 。 四、计算 19.学习了简单机械的有关知识后,小强同学自制了一种简易升降晾衣架,它由4个定滑轮和两个动滑轮组成,绳子的一端固定在天花板上,人用力拉绳子的自由端可以使晾衣架匀速上升,晾衣架在匀速上升过程中横梁保持水平,如图所示,将40N的衣物挂在晾衣架上,人拉绳的力为12.5N时,衣物匀速上升,忽略绳重及摩擦,求: (1)此时该装置的机械效率; (2)将60N的衣物挂在晾衣架上,使其在5s匀速升高1m,人所做的总功和功率各是多少? 20.如图所示,现将一重G1=8100N的实心铝块在水中匀速上提h=2m(未露出水面),已知每个滑轮重G2=900N,不计绳重和各种摩擦,不计水的阻力。已知铝的密度ρ铝=2.7×103kg/m3,水的密度ρ水=1.0×103kg/m3,g取10N/kg。求: (1)滑轮组的机械效率多大? (2)若绳端拉力的功率为P=540W,则铝块上升的速度为多大? 【答案与解析】 一、选择 1.【答案】B 【解析】手是一个杠杆时,如图所示:支点O在腕关节处;球压在掌心上的力是阻力F2,方向竖直向下;过支点作阻力F2 的垂线得到的线段即为阻力臂L2;前臂中的屈肌收缩产生的动力F1,方向水平向右;过支点作动力F1的垂线得到的线段即为动力臂L1;由图可知:阻力臂很明显大于动力臂。所以是费力杠杆,费力杠杆的特点是:省距离。 2.【答案】B 【解析】A、有用功与总功的比值叫机械效率,故机械效率与做功的多少无关,此选项错误;
B、功率反映做功的快慢,功率大则做功快,功率小,则做功慢,此选项正确;
C、机械效率与机械功率大小没有直接关系,此选项错误;
D、功率等于功和做功时间的比值,时间短,功多少不确定,功率大小不确定,此选项错误。
3.【答案】D 【解析】原来水平平衡: 去掉相同质量的物体后,杠杆左边:;杠杆右边; 因为所以 , 则:?,所以杠杆右端下降;把支点向右移动,可使杠杆平衡。 4.【答案】B
【解析】选项A和B中各是一个杠杆,其中A图中的杠杆的动方臂大于阻力臂,是一个省力杠杆,故F1<G;而B图中的杠杆是一个费力杠杆,故F2>G;选项C中是一个定滑轮,定滑轮不省力,故F3=G;选项D中是一个动滑轮,可以省一半的力,故F4<G。综上所述,F2最大。 5.【答案】B 【解析】根据滑轮组省力知识,依题:。 6.【答案】D 【解析】A、B 剪刀可以看做是一个杠杆,根据杠杆的平衡条件F1L1=F2L2知,要比较动力或阻力大小,必须知道动力臂和阻力臂;A、B选项都错误;C、D 利用剪刀的目的是剪纸,所以剪纸做的功是有用功;由机械效率为80%知,如果动力做功1J,有0.8J是用于剪纸。C选项错误,D选项正确。 7.【答案】C 【解析】A、使用任何机械都不省功;机械效率是指有用功与总功的比值,机械效率的高低与是否省力没有必然的联系,故A错误;BD、做功越快的机械,说明功率大,与机械效率没有必然联系,不能确定机械效率的高低;根据机械效率的高低也不能确定做功的快慢;故BD错误;C、根据 和 W总=W有+W额可知,额外功相同时,有用功越大的机械效率越高,故C正确,故选C。 8.【答案】D 9.【答案】C 【解析】因为小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,所以两种情况的有用功相同;当有用功一定时,利用机械时做的额外功越少,则总功越少,机械效率越高。又因乙滑轮是动滑轮,所以利用乙滑轮做的额外功多,则总功越多,机械效率越低,即W1<W2,η1>η2,所以C选项正确。 10.【答案】A 【解析】有用功;总功; 机械效率: 。 二、填空 11.【答案】C;200;靠近 【解析】用固定在墙上的三角支架ABC放置空调室外机。如果A处螺钉松脱,则支架会绕C点倾翻; C点是支点,空调的自身重力是阻力,在阻力与阻力臂一定的情况下,由杠杆平衡条件可知,动力臂越大,动力越小,;;所以F=200N;为了安全,室外机的位置应尽量靠近墙壁,以减小阻力臂,从而减小A处的拉力。 12.【答案】省力;省距离;②④⑥ 【解析】人们使用动力臂比阻力臂长的杠杆是为了省力;有时却要使用费力杠杆,那又是为了省距离; ①天平在使用过程中,动力臂等于阻力臂,是等臂杠杆;②扳手、④羊角锤、⑥瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆;③镊子、⑤裁衣剪刀、⑦筷子、⑧钓鱼杆在使用过程中,动力臂小于阻力臂,是费力杠杆;故答案为:省力;省距离;②④⑥。 13.【答案】1;30 【解析】(1)由图知,n=3,则,重物升高:, 重物上升的速度:。 (2)因为:,所以动滑轮重:。 14.【答案】50;20 【解析】物体在50N的推力作用下,在水平方向做匀速直线运动,所以摩擦力等于推力,也是50N; 物体移动的速度为; 小童做功的功率为P=Fv=50N×0.4m/s=20W。 15.【答案】(1)1;(2)1.25 【解析】(1)如果直接把物体提升0.2m,需要做功:, 使用斜面做的功:; 不考虑摩擦有用功等于总功,即:,则拉力:。 (2)直接把物体提升0.2m所做的功为有用功:, 机械效率:,得总功;则拉力:。 16.【答案】90%;700;0.2 【解析】(1)已知:,,g=10N/Kg, 物体A的重力为:, 动滑轮的重力为:, 从图可知,该滑轮组有3段绳子吊着物体,所以提升物体A时小刚对绳子的拉力为:,
则提升物体A时,滑轮组的机械效率为:。 (2)此时小刚受竖直向上的支持力和竖直向下的重力和拉力,则小刚对高台的压力等于他的体重加上绳子对他的拉力,而,则小刚的重力为:, 所以小刚对高台的压力为:。 (3))物体B的重力为:, 则提升物体B时小刚对绳子的拉力为:, 而拉力做功的功率为, 拉力上升的速度为:, 则物体B上升的速度为:。 三、实验探究 17.【答案】(1)右;力臂;(2)1;(3)B 【解析】(1)杠杆重心左移应将平衡螺母向右调节,直至重心移到支点处;由于力臂是支点到力的作用线的垂直距离,调节杠杆在水平位置平衡时,可以方便的读出力臂; (2)第三组的阻力为; (3)“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”,是在杠杆在水平位置平衡 且动力和阻力的方向都是竖直向下的条件下得出的,也就是实验过程中没有改变动力或阻力的方向。故选项A、C、D错误,选项B正确。 18.【答案】(1)90.9%;(2)增大;减小;(3)滑轮与轮轴间有摩擦、绳子有重力 【解析】(1)由表中实验数据可知,第②次实验时,动滑轮的机械效率: 。
(2)由表中实验序号为①②的实验数据可知,对于同一动滑轮,所提升钩码的重力增大,机械效率将增大;由表中实验序号为②③的实验数据可知,提升相同重力的钩码时,动滑轮的重力增大,其机械效率将减小。
(3)由于滑轮与轮轴间存在摩擦、缠绕滑轮组的绳子有重力,因此。 四、计算 19.【答案与解析】:(1)由图可知,n=4,则该装置的机械效率: ; (2)由可得,晾衣架的重力:G衣架=4F-G=4×12.5N-40N=10N, 人所做的总功:W总′=(G′+G衣架)h=(60N+10N)×1m=70J, 人所做功的功率:。 答:(1)此时该装置的机械效率为80%;(2)功率是14W。 20.【答案与解析】(1)铝块重的质量:, 铝块的体积:; 在水中铝块受到的浮力:; 滑轮组对铝块的拉力:; 使用滑轮组做的有用功:, 不计绳重和各种摩擦,使用滑轮组做的额外功:; ;滑轮组的机械效率:; (2)根据公式:,可得做功时间:; 铝块上升的速度:。 答:(1)滑轮组的机械效率85%;(2)铝块上升的速度为0.09m/s。
一、杠杆 1.杠杆:一根在力的作用下能绕着固定点转动的硬棒就是杠杆。杠杆的五要素是:支点、动力、阻力、动力臂和阻力臂,杠杆可以是直的硬棒,如撬棒等;也可以是弯的,如羊角锤。 2.杠杆的五要素: (1)支点:杠杆绕着转动的点,即图中的O点. (2)动力:使杠杆转动的力,即图中的F1。 (3)阻力:阻碍杠杆转动的力,即图中的F2。 (4)动力臂:从支点到动力作用线的距离,即图中的。 (5)阻力臂:从支点到阻力作用线的距离,,即图中的。 3.杠杆的平衡条件是:动力×动力臂=阻力×阻力臂,用字母表示为:;杠杆的平衡不是单独由力或力臂决定的,而是由它们的乘积来决定的。 4.杠杆分类:
(1)省力杠杆:>,F1<F2。
这类杠杆的特点是动力臂大于阻力臂,平衡时动力F1小于阻力F2,即用较小的动力就可以克服较大的阻力。但是实际工作是动力移动的距离却比阻力移动的距离大,即要费距离。如撬起重物的撬棒,开启瓶盖的起子、铡草用的铡刀等,都属于这一类杠杆。
(2)费力杠杆:<,F1>F2。
这类杠杆的特点是动力臂小于阻力臂,平衡时动力F1大于阻力F2,即要用较大的动力才能克服阻力完成工作,但它的优点是杠杆工作时,动力移动较小的距离就能使阻力移动较大的距离。使工作方便,也就是省了距离。如缝纫机踏板、挖土的铁锨、大扫帚、夹煤块的火钳,这些杠杆都是费力杠杆。
(3)等臂杠杆:=,F1=F2。
这类杠杆的动力臂等于阻力臂,平衡时动力F1等于阻力F2,工作时既不省力也不费力,如天平、定滑轮就是等臂杠杆。 注: 1.力臂的画法: (1)明确支点,用O表示 ; (2)通过力的作用点沿力的方向画一条直线; (3)过支点O作该力的作用线的垂线; (4)用两头带箭头的线段标示出支点到力的作用线的垂线段,写上相应的字母(或)。
2.杠杆的平衡:杠杆在力的作用下保持静止或匀速转动,杠杆就处于平衡状态。
3.杠杆的平衡条件也称为杠杆的原理,最早是由古希腊学者阿基米德总结出来的。 二、滑轮 1.定滑轮: (1)定义:工作时,轴的位置固定不动的滑轮,称为定滑轮。 (2)实质:如图甲所示,我们可把一条直径看成杠杆,圆心就是杠杆的支点,因此,定滑轮实质是等臂杠杆。 (3)作用:不能省力,但可以改变用力方向。 2.动滑轮: (1)定义:轴的位置随被拉动的物体一起运动的滑轮,称为动滑轮。 (2)实质:如图乙所示,它实质是动力臂为阻力臂2倍的省力杠杆,它的转动轴是阻力作用点。 (3)作用:可以省力,但是不能改变力的方向。 3.滑轮组: (1)组成:定滑轮和动滑轮 (2)作用:既可以改变力的大小又可以改变力的方向 (3)滑轮组绳子自由端的拉力:(忽略绳子重和摩擦)。 (4)物体上升的高度h与绳子自由端移动的距离s的关系:。 注: 1. 组装滑轮组,在知道或算出滑轮组承担重物的绳子段数情况下,根据“奇动偶定”的原则,先确定绳子的一端是挂在动滑轮或定滑轮的钩上,再由里向外顺次绕线。 2.时间t内,物体上升高度h,绳子自由端移动的距离s;物体移动的速度,绳子自由端移动的速度;所以物体上升的速度与绳子自由端移动的速度关系:。 三、功 1.做功的两个必要因素:
(1)作用在物体上的力;
(2)物体在力的方向上通过的距离。
2.不做功的三种情况
(1)物体受力,但物体没有在力的方向上通过距离。此情况叫“劳而无功”。
(2)物体移动了一段距离,但在此运动方向上没有受到力的作用(如物体因惯性而运动)。此情况叫“不劳无功”。
(3)物体既受到力,又通过一段距离,但两者方向互相垂直(如起重机吊起货物在空中沿水平方向移动)。此情况叫“垂直无功”。 3.功的计算:
(1)公式:一般式 W=Fs ;常用式 W=Gh(克服重力做功)或W=f阻s(克服摩擦阻力做功)。
(2)单位:焦耳(J) 4.注意事项: (1)F与s的方向应在同一直线上(初中要求)(比如一个人提着一重物G,从山脚顺着“之”字形的山路爬到山顶,此时人克服重力做功所移动的距离并不是山路的长,而是从山脚到山顶的高)
(2)做功的多少,由W=Fs决定,而与物体的运动形式无关。
注: 1.判断物体做功的依据:做功的两个必要因素,重点抓住力作用在物体上是否有“成效”。 2.在分析做功情况时还应注意以下几点:
(1)当物体的受力方向与运动方向不垂直时,这个力就要做功。
(2)一个物体同时受几个力的作用时,有一些力做了功,有些力没有做功。因此,讲做功必须指出是哪一个力对哪一个物体做功。
(3)什么叫物体克服阻力做功:若物体在运动方向上受到一个与此方向相反的力F的作用,我们通常说物体克服阻力F做了功。
比如:物体在竖直向上运动h的过程中,物体克服重力做功,功的大小为W=Gh; 再如:物体在水平方向上向前运动s,物体克服摩擦力做功,功的大小为W=fs。 四、功率
1.物理意义:表示物体做功的快慢。 2.定义:物体在单位时间内所做的功。 3.计算式:, P 表示功率,W 表示功,t 表示时间,使用公式计算功率时,必须注意W 和t的对应关系。W 为在t时间内所做的功,而t为做W 这么多的功所用的时间。 4.推导式:,式中F为做功的力而v为速度。 5.单位:瓦(W) 注: 1.注意区别功与功率。功率与功是两个不同的物理量,“功”表示做功的“多少”,而“功率”则表示做功的“快慢”,“多少”与“快慢”的意义不一样。只有在做功时间相同时,做功多的就做功快。否则,做功多,不一定做功就快,即“功率”不一定就大。也就是说:功率与功和时间两个因素有关。
2.由P=W/t变形为P=Fv可知:功率一定时,力F与速度v成反比。 五、机械效率 1.机械效率:有用功与总功的比值叫作机械效率。 2. 公式为: 3.推导式: (1)竖直方向匀速提升物体时,滑轮组的机械效率:, 忽略绳重和摩擦,绳子自由端的拉力:, 滑轮组的机械效率:。 (2)水平方向匀速拉物体时如图所示,滑轮组的机械效率:。 (3)斜面的机械效率:, 注:? 1.机械效率是有用功在总功中所占的比例,其大小是由有用功和总功共同决定的,在比较机械效率大小时,可采用控制变量法,相同时,越大,越小;相同时,越大,越大。 2.判断有用功和额外功,必须抓住工作的目的,为达到目的必须做的功就是有用功,但对我们没有用而不得不做的功就是额外功。并要注意工作目改变了,有用功和额外功也要发生变化。 3.提高机械的机械效率的方法:改进机械结构,尽量减小机械自重,合理使用机械,按规定进行保养以减小摩擦。 4.需要注意的几个问题: (1)机械效率只有大小没有单位; (2)由于有用功总小于总功,所以机械效率总小于1,通常用百分数表示; (3)机械效率是标志机械做功性能的好坏的物理量之一,机械效率越高,做的有用功占总功的比例就越大这个机械的做功性能就越好。 【典型例题】 例1.如图所示在用羊角锤拔钉子时,若O为支点,画出在A点施加的最小力F的示意图及其力臂L。 【答案与解析】1.确定杠杆中的支点和动力作用点的位置;2.连接支点与动力作用点,即连接AO,得到最长的线段;3.经过动力作用点做出与该线段垂直的直线。 例2.如图所示,唐师傅想用最省力的方法把一个油桶推上台阶,请你在图中画出这个力的示意图。 【答案与解析】在处理此类杠杆中最小力的问题时,可按以下步骤进行:①确定支点和动力作用点;
②过动力作用点做出与动力臂垂直的直线,即动力作用线。 例3.假期里明明和他爸爸、妈妈一起参加了一个家庭游戏活动。活动的要求是:家庭成员中的任意两名成员分别站在如图所示的木板上,恰好使木板水平平衡。
(1)若明明和爸爸的体重分别为350N和700N,明明站在左侧离中央支点3m处,明明的爸爸应站在哪一侧?应离中央支点多远才能使木板水平平衡?
(2)若明明和他爸爸已经成功地站在了木板上,现在他们同时开始匀速相向行走,明明的速度是0.4m/s,爸爸的速度是多大才能使木板水平平衡不被破坏? 【答案与解析】(1)明明和爸爸对杠杆施加的力分别为F1=350N,F2=700N,F1的力臂L1=3m,
根据杠杆平衡条件:F1L1=F2L2, 即:350N×3m=700N×L2, 所以,L2=1.5m, 答:爸爸站在距离支点1.5m的另一侧。 (2)设:明明和爸爸匀速行走的速度分别为v1和v2, 行走时间为t,要保证杠杆水平平衡, 则有F1(L1-v1t)=F2(L2-v2t) 350N(3m-0.4m/s×t)=700N(1.5m-v2t) 解得:v2=0.2m/s。 答:明明和爸爸匀速相向行走,明明的速度是0.4m/s,爸爸的速度是0.2m/s才能使木板水平平衡不被破坏。 例4.如图所示,一个厚度均匀的薄木板长2m,木块右端用一根绳子悬挂。绳子所能承受的最大拉力为10N。一个大小不计的木块重40N,它从木块左边的O点开始以0.2m/s的速度向木板右端匀速移动,求:木块运动多长时间绳子断裂?(木板重力不计)。 【答案与解析】根据杠杆的平衡条件:,可得:; 由公式,可得:。 答:木块运动2.5s后绳子断裂。 例5.如图所示,重为500N的某人站在重为350N的木板上,木板成水平状态,整个装置在空中保持静止,每个滑轮自重为50N,不计摩擦和绳重,则人对木板的压力大小为 N。 【答案】300 【解析】方法一:(1)对人、板、滑轮1受力分析图1:,可得:F=450N; (2)对滑轮1受力分析图2:,可得:; (3)对人受力分析图3:,可得:; 因为人受到的支持力和人对板的压力是一对相互作用力大小相等,所以人对板的压力是300N。 方法二:人的重力500N+木板的重力350N+下面的滑轮的重力50N=900N,读图可知,这900N都由最上面的滑轮承担,而且左右拉力相等。因此,上面滑轮右侧的拉力为450N,减去下面滑轮的自重50N,等于400N.这400N又由两段绳子平均分担,因此,人手处的拉力为200N。于是得出,人对木板的压力=人的重力500N-绳子拉人手的力200N=300N。 例6.如图所示,站在小车上的男孩在绳子末端施加50N的水平拉力F,物体M和小车在水平地面上做相向的匀速直线运动,物体M速度为0.2m/s,小车速度为0.3m/s,则地面对物体M的摩擦力为 N,2s后绳子自由端移动的距离为 m。(不计绳重、滑轮重以及绳与滑轮的摩擦) 【答案】150;3 例7.小勇同学利用星期天积极参加社会实践活动,到养老院当义工,在活动中要帮助老人将3壶相同的油从一楼搬到三楼。小勇第一趟将一壶油从一楼提到三楼,用时20s;第二趟将两壶油从一楼提到三楼,用时30s。已知每壶油的质量为5kg,小勇的质量为45kg,每层楼的楼高是3m。(g=10N/kg) (1)第一趟小勇做了多少有用功?小勇做功的总功率是多少? (2)比较小勇两趟做功效率的高低,并说明理由。 【答案与解析】 (1)第一趟做的有用功:; 第一趟做的总功:; 总功的功率:。 (2)第二趟做功效率高。 理由:小勇两次克服自己体重做的额外功不变,第二趟提两壶油增大了有用功,从而增大有用功在总功中的比值,所以第二趟做功效率高; 答:(1)第一趟小勇做了300J的有用功;小勇做功的总功率是150W。(2)第二趟做功效率高。 理由:小勇两次克服自己体重做的额外功不变,第二趟提两壶油增大了有用功,从而增大有用功在总功中的比值,所以第二趟做功效率高。 例8.一辆车开进了泥潭中,司机取来一个动滑轮欲将汽车从泥潭中拉出,如图所示,若司机用750N的拉力在5s内将汽车水平匀速拉动1m,那么司机所做的功是 J,司机做功的功率是 W,若滑轮的机械效率为60%,汽车所受地面的摩擦力是 N。 【答案】1500;300;900 例9.为了将放置在水平地面上、重G=100N的重物提升到高处。小明同学设计了图甲所示的滑轮组装置。当小明用图乙所示随时间变化的竖直向下拉力F拉绳时,重物的速度υ和上升的高度h随时间t变化的关系图象分别如图丙和丁所示.若重物与地面的接触面积S=5×10-2m2,不计摩擦,绳对滑轮的拉力方向均可看成在竖直方向。求: (1)在1~2s内,若重物上升1.25m,拉力F做的功W。 (2)在2~3s内,拉力F的功率P及滑轮组的机械效率η。 (3)若绳子能承受的最大拉力是1500N,小李体重600N,他站在地面向下拉绳子使物体匀速上升,最大能提升多重的物体? 【答案与解析】(1)在1~2s内,拉力F1=50N,重物上升高度h1=1.25m; 拉力F的作用点下降的距离, 拉力做的功:; 绳子自由端的拉力:, 动滑轮的重力为:; (2)由图可知在2~3s内,重物做匀速运动,,拉力,
∵从动滑轮上直接引出的绳子股数(承担物重的绳子股数)n=3, ∴拉力F的作用点下降的速度, 拉力做功功率(总功率):; 滑轮组的机械效率: (3)绳子能承受的最大拉力是1500N,所以物体的最大重力为:; 所以:。
答:(1)在1~2s内,拉力F做的功为187.5J;
(2)在2~3s内,拉力F的功率为300W,滑轮组的机械效率为83.3%;
(3)最大能提升1750N的物体。 例10.如图甲所示的滑轮组。不计绳重和摩擦,物体重G从400N开始逐渐增加,直到绳子被拉断。每次均匀速拉动绳子将物体提升同样的高度。图乙记录了在此过程中滑轮组的机械效率随物体重力的增加而变化的图象。 (1)当滑轮组的机械效率为40%时,绳子的拉力为多大? (2)2个滑轮总重多少? (3)绳子能承受的最大拉力是多少? (4)当滑轮组的机械效率为80%时,物体重多少? 【答案与解析】(1)从甲图中可知,n=4;从乙图中可知,当η=40%时,G=400N, 根据机械效率:,即:。 (2)设两个动滑轮总重G总,则, 即:。 (3)由乙图可知:当物重最大为G′=3200N时,绳子刚好被拉断,则绳子能承受的最大拉力:
。 (4)根据机械效率:,可得:。
答:(1)当滑轮组的机械效率为40%时,绳子的拉力为250N; (2)2个滑轮总重600N; (3)绳子能承受的最大拉力是950N; (4)当滑轮组的机械效率为80%时,物体重2400N。 例11.某同学用如图所示的实验装置测量滑轮组的机械效率,相关数据记录在下表中, (1)实验中,使用滑轮组提升重物时,应竖直向上 拉动弹簧测力计。 (2)第三次实验中,绳端移动的距离为 m,滑轮组的机械效率为 。 (3)分析实验数据发现,同一滑轮组提升重物的重力变大时,滑轮组的机械效率将 (选填“变大”“变小”或“不变”)。 【答案】(1)匀速;(2)0.45m;80%;(3)变大 【解析】(1)实验中应该匀速竖直向上拉动弹簧测力计,以保证拉力大小恒定。 (2)由图示可知,滑轮组承重绳子有效股数n=3, 第3次测量中,弹簧测力计移动的距离s=nh=3×0.15m=0.45m; 滑轮组的机械效率; (3)根据第1次和第2次数据可知,机械效率分别为: ; ; 两次所用滑轮组相同,但第2次物重大于第1次物重,机械效率也大于第1次的机械效率,所以可得使用同一滑轮组,提高物重可以提高滑轮组的机械效率;答案为:(1)匀速;(2)0.45m;80%;(3)变大。 【复习训练】 一、选择 1.当你用手掌托住一只铁球并绕腕关节向上转动时,手就是一个杠杆、球压在掌心上的力是阻力,腕关节是支点,通过前臂中的伸、屈肌的伸、缩产生动力,使托住球的手向上转动(如图)。那么,人体上的这个杠杆应该是( ) A.省力杠杆 B.省距离杠杆 C.既省力又省距离的杠杆 D.既不省力也不省距离的杠杆 2.下列关于功、功率、机械效率的说法正确的是( ) A.做功多的机器机械效率一定高 B.功率小的机器做功慢 C.机械效率高的机器功率一定大 D.功率大的机器做功时间一定短 3. 如图,杠杆在水平位置平衡,若在杠杆两端各取掉相同质量的物体,则( ) A.杠杆左端下降;把支点向左移动,可使杠杆平衡 B.杠杆左端下降;把支点向右移动,可使杠杆平衡 C.杠杆右端下降;把支点向左移动,可使杠杆平衡 D.杠杆右端下降;把支点向右移动,可使杠杆平衡 4.用下图所示的简单机械,使重量同为G的物体都处于静止状态,其中用力最大的是(均不计摩擦)( )
5.如图所示,甲、乙两滑轮组,它们吊起的重物都是G,滑轮重量及摩擦不计,当重物匀速上升时,两滑轮组绳端拉力分别为F甲、F乙,那么F甲:F乙是( ) A. 1:1 B. 2:3 C. 3:2 D. 1:3 6.图中的剪刀剪纸机械效率为80%,这表示( ) A.若作用在剪刀的动力是1N,则阻力是0.8N B.若作用在剪刀的阻力是1N,则动力是0.8N C.若作用在剪刀的动力做功1J,则有0.2J?的功用于剪纸 D.若作用在剪刀的动力做功1J,则有0.8J?的功用于剪纸 7.下列说法中正确的是( ) A.省力的机械不能省功,机械越省力,其机械效率越高 B.做功越快的机械,虽然它做的功不一定多,但是其机械效率是越高的 C.做相同的额外功时,有用功越大的机械效率越高 D.机械效率越低的时候,做功一定是越慢的 8. 一个滑轮组经改进后提高了机械效率,用它把同一物体匀速提升同样的高度,改进后与改进前相比( ) A.有用功减少,总功减少 B.有用功增加,总功增加 C.有用功不变,总功不变 D.有用功不变,总功减少 9.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为W1,机械效率为η1;用乙滑轮所做的总功为W2,机械效率为η2。若不计绳重与摩擦,则( )
A.W1=W2,η1=η2 B.W1=W2,η1<η2 C.W1<W2,η1>η2 D.W1>W2,η1<η2 10.利用如图所示装置将重为100N的物体匀速从斜面的底端拉到顶端.已知斜面的长是5m,高是2m,拉力为F=50N,则该装置的机械效率为( ) A.40% B.50% C.80% D.100% 二、填空 11.如图所示,用固定在墙上的三角支架ABC放置空调室外机。如果A处螺钉松脱,则支架会绕 点倾翻。已知AB长40cm,AC长30cm。室外机的重力为300N,正好处在AB中点处,则A处螺钉的水平拉力为 N(支架重力不计)。为了安全,室外机的位置应尽量 (选填“靠近”或“远离”)墙壁。 12.杠杆在我国古代早就有了许多巧妙的应用,有时人们使用动力臂比阻力臂长的杠杆是为了 ;有时却要使用费力杠杆,那又是为了 。下列工具中①天平、②扳手、③镊子、④羊角锤、⑤裁衣剪刀、⑥瓶盖起子、⑦筷子、⑧钓鱼杆等都是简单机械,其中属于省力杠杆的是 。(填序号) 13.如图所示,某人将重为150N的物体匀速提起,在2s内绳的自由端移动了6m,则重物上升的速度为 m/s,若拉绳的力为60N,则动滑轮重为 N。(不计绳重和摩擦) 14.小童同学用50N的水平推力,使放在水平桌面上重200N的物体做匀速直线运动,若该物体在10s内移动4m,则在此过程中,物体受到的摩擦力是 N,小童做功的功率是 W。 15.如图所示,用平行于斜面的拉力F,将重为2N的物体沿斜面从底端匀速拉至顶端。若不考虑物体与斜面间的摩擦,则拉力F为 N;若斜面的机械效率为80%,则此时拉力F为 N。 16.如图所示,小刚站在高台上通过滑轮组先后竖直向上匀速提升物体A和物体B。假设在拉绳子的过程中,小刚对绳子的拉力与对高台的压力始终在同一直线上,不计绳重和摩擦。已知小刚的质量为50kg,物体A的质量为54kg,物体B的质量为84kg,动滑轮的质量为6kg。当提升物体A时,滑轮组的机械效率为 ,此时小刚对高台的压力是 N;当提升物体B时,小刚拉力做功的功率为180W,则物体B上升的速度为 m/s。(g取10N/Kg) 三、实验探究 17.物理实验小组的同学,利用如图所示的装置,在杠杆支点的两边分别挂上钩码来探究杠杆的平衡条件。
(1)如图甲所示,为使杠杆在水平位置平衡,应将右端的平衡螺母向 (选填“左”或“右”)移动,将杠杆调在水平位置的目的是为了方便测量 。 (2)实验中测得的数据如表所示,表格中漏填的数据为 N。 ?测量序号?动力F1/N?动力臂l1/cm阻力F2/N??阻力臂l2/cm?①?1?20?2?10?②?2?15?1.5?20?③?3?5??15
(3)有的同学按现有方案得出如下结论:“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”。这个结论与杠杆平衡条件不符,原因是实验过程中 (填字母)。 A.没有改变力的大小?????? B.没有改变力的方向 C.没有改变力的作用点???? D.实验次数较少,结论具有偶然性 18.用如图所示装置测量动滑轮的机械效率。实验时,竖直向上的匀速拉动弹簧测力计,使挂在动滑轮下面的钩码缓缓上升。实验数据如下表。 序号动滑轮重G动/N钩码重力G/N钩码上升高度h/m绳的拉力F/N绳端移动距离s/m?机械效率η①0.110.20.60.483.3%②0.120.21.10.4③0.220.21.20.483.3%
(1)第②次实验时,测得动滑轮的机械效率约为 。
(2)分析表中数据可知,对于同一动滑轮,所提升钩码的重力增大,机械效率将 ;提升相同重力的钩码时,动滑轮的重力增大,其机械效率将 。(选填“增大”“减小”或“不变”)
(3)分析表中数据可知,,可能的原因是: 。 四、计算 19.学习了简单机械的有关知识后,小强同学自制了一种简易升降晾衣架,它由4个定滑轮和两个动滑轮组成,绳子的一端固定在天花板上,人用力拉绳子的自由端可以使晾衣架匀速上升,晾衣架在匀速上升过程中横梁保持水平,如图所示,将40N的衣物挂在晾衣架上,人拉绳的力为12.5N时,衣物匀速上升,忽略绳重及摩擦,求: (1)此时该装置的机械效率; (2)将60N的衣物挂在晾衣架上,使其在5s匀速升高1m,人所做的总功和功率各是多少? 20.如图所示,现将一重G1=8100N的实心铝块在水中匀速上提h=2m(未露出水面),已知每个滑轮重G2=900N,不计绳重和各种摩擦,不计水的阻力。已知铝的密度ρ铝=2.7×103kg/m3,水的密度ρ水=1.0×103kg/m3,g取10N/kg。求: (1)滑轮组的机械效率多大? (2)若绳端拉力的功率为P=540W,则铝块上升的速度为多大? 【答案与解析】 一、选择 1.【答案】B 【解析】手是一个杠杆时,如图所示:支点O在腕关节处;球压在掌心上的力是阻力F2,方向竖直向下;过支点作阻力F2 的垂线得到的线段即为阻力臂L2;前臂中的屈肌收缩产生的动力F1,方向水平向右;过支点作动力F1的垂线得到的线段即为动力臂L1;由图可知:阻力臂很明显大于动力臂。所以是费力杠杆,费力杠杆的特点是:省距离。 2.【答案】B 【解析】A、有用功与总功的比值叫机械效率,故机械效率与做功的多少无关,此选项错误;
B、功率反映做功的快慢,功率大则做功快,功率小,则做功慢,此选项正确;
C、机械效率与机械功率大小没有直接关系,此选项错误;
D、功率等于功和做功时间的比值,时间短,功多少不确定,功率大小不确定,此选项错误。
3.【答案】D 【解析】原来水平平衡: 去掉相同质量的物体后,杠杆左边:;杠杆右边; 因为所以 , 则:?,所以杠杆右端下降;把支点向右移动,可使杠杆平衡。 4.【答案】B
【解析】选项A和B中各是一个杠杆,其中A图中的杠杆的动方臂大于阻力臂,是一个省力杠杆,故F1<G;而B图中的杠杆是一个费力杠杆,故F2>G;选项C中是一个定滑轮,定滑轮不省力,故F3=G;选项D中是一个动滑轮,可以省一半的力,故F4<G。综上所述,F2最大。 5.【答案】B 【解析】根据滑轮组省力知识,依题:。 6.【答案】D 【解析】A、B 剪刀可以看做是一个杠杆,根据杠杆的平衡条件F1L1=F2L2知,要比较动力或阻力大小,必须知道动力臂和阻力臂;A、B选项都错误;C、D 利用剪刀的目的是剪纸,所以剪纸做的功是有用功;由机械效率为80%知,如果动力做功1J,有0.8J是用于剪纸。C选项错误,D选项正确。 7.【答案】C 【解析】A、使用任何机械都不省功;机械效率是指有用功与总功的比值,机械效率的高低与是否省力没有必然的联系,故A错误;BD、做功越快的机械,说明功率大,与机械效率没有必然联系,不能确定机械效率的高低;根据机械效率的高低也不能确定做功的快慢;故BD错误;C、根据 和 W总=W有+W额可知,额外功相同时,有用功越大的机械效率越高,故C正确,故选C。 8.【答案】D 9.【答案】C 【解析】因为小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,所以两种情况的有用功相同;当有用功一定时,利用机械时做的额外功越少,则总功越少,机械效率越高。又因乙滑轮是动滑轮,所以利用乙滑轮做的额外功多,则总功越多,机械效率越低,即W1<W2,η1>η2,所以C选项正确。 10.【答案】A 【解析】有用功;总功; 机械效率: 。 二、填空 11.【答案】C;200;靠近 【解析】用固定在墙上的三角支架ABC放置空调室外机。如果A处螺钉松脱,则支架会绕C点倾翻; C点是支点,空调的自身重力是阻力,在阻力与阻力臂一定的情况下,由杠杆平衡条件可知,动力臂越大,动力越小,;;所以F=200N;为了安全,室外机的位置应尽量靠近墙壁,以减小阻力臂,从而减小A处的拉力。 12.【答案】省力;省距离;②④⑥ 【解析】人们使用动力臂比阻力臂长的杠杆是为了省力;有时却要使用费力杠杆,那又是为了省距离; ①天平在使用过程中,动力臂等于阻力臂,是等臂杠杆;②扳手、④羊角锤、⑥瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆;③镊子、⑤裁衣剪刀、⑦筷子、⑧钓鱼杆在使用过程中,动力臂小于阻力臂,是费力杠杆;故答案为:省力;省距离;②④⑥。 13.【答案】1;30 【解析】(1)由图知,n=3,则,重物升高:, 重物上升的速度:。 (2)因为:,所以动滑轮重:。 14.【答案】50;20 【解析】物体在50N的推力作用下,在水平方向做匀速直线运动,所以摩擦力等于推力,也是50N; 物体移动的速度为; 小童做功的功率为P=Fv=50N×0.4m/s=20W。 15.【答案】(1)1;(2)1.25 【解析】(1)如果直接把物体提升0.2m,需要做功:, 使用斜面做的功:; 不考虑摩擦有用功等于总功,即:,则拉力:。 (2)直接把物体提升0.2m所做的功为有用功:, 机械效率:,得总功;则拉力:。 16.【答案】90%;700;0.2 【解析】(1)已知:,,g=10N/Kg, 物体A的重力为:, 动滑轮的重力为:, 从图可知,该滑轮组有3段绳子吊着物体,所以提升物体A时小刚对绳子的拉力为:,
则提升物体A时,滑轮组的机械效率为:。 (2)此时小刚受竖直向上的支持力和竖直向下的重力和拉力,则小刚对高台的压力等于他的体重加上绳子对他的拉力,而,则小刚的重力为:, 所以小刚对高台的压力为:。 (3))物体B的重力为:, 则提升物体B时小刚对绳子的拉力为:, 而拉力做功的功率为, 拉力上升的速度为:, 则物体B上升的速度为:。 三、实验探究 17.【答案】(1)右;力臂;(2)1;(3)B 【解析】(1)杠杆重心左移应将平衡螺母向右调节,直至重心移到支点处;由于力臂是支点到力的作用线的垂直距离,调节杠杆在水平位置平衡时,可以方便的读出力臂; (2)第三组的阻力为; (3)“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”,是在杠杆在水平位置平衡 且动力和阻力的方向都是竖直向下的条件下得出的,也就是实验过程中没有改变动力或阻力的方向。故选项A、C、D错误,选项B正确。 18.【答案】(1)90.9%;(2)增大;减小;(3)滑轮与轮轴间有摩擦、绳子有重力 【解析】(1)由表中实验数据可知,第②次实验时,动滑轮的机械效率: 。
(2)由表中实验序号为①②的实验数据可知,对于同一动滑轮,所提升钩码的重力增大,机械效率将增大;由表中实验序号为②③的实验数据可知,提升相同重力的钩码时,动滑轮的重力增大,其机械效率将减小。
(3)由于滑轮与轮轴间存在摩擦、缠绕滑轮组的绳子有重力,因此。 四、计算 19.【答案与解析】:(1)由图可知,n=4,则该装置的机械效率: ; (2)由可得,晾衣架的重力:G衣架=4F-G=4×12.5N-40N=10N, 人所做的总功:W总′=(G′+G衣架)h=(60N+10N)×1m=70J, 人所做功的功率:。 答:(1)此时该装置的机械效率为80%;(2)功率是14W。 20.【答案与解析】(1)铝块重的质量:, 铝块的体积:; 在水中铝块受到的浮力:; 滑轮组对铝块的拉力:; 使用滑轮组做的有用功:, 不计绳重和各种摩擦,使用滑轮组做的额外功:; ;滑轮组的机械效率:; (2)根据公式:,可得做功时间:; 铝块上升的速度:。 答:(1)滑轮组的机械效率85%;(2)铝块上升的速度为0.09m/s。
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
