人教版七年级数学上册第四章几何图形初步4.3.3余角和补角课件(共19张)
文档属性
| 名称 | 人教版七年级数学上册第四章几何图形初步4.3.3余角和补角课件(共19张) |  | |
| 格式 | zip | ||
| 文件大小 | 536.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-30 08:05:38 | ||
图片预览





文档简介
课件19张PPT。 北京新机场比萨斜塔建于1173年,工程曾间断了两次,历经约二百年才完工,设计为垂直建造,但是在工程开始后不久便由于地基不均匀和土层松软而倾斜,你知道比萨斜塔倾斜多少度角吗?
它现在与地面成多少度角?倾斜了约3.97°.
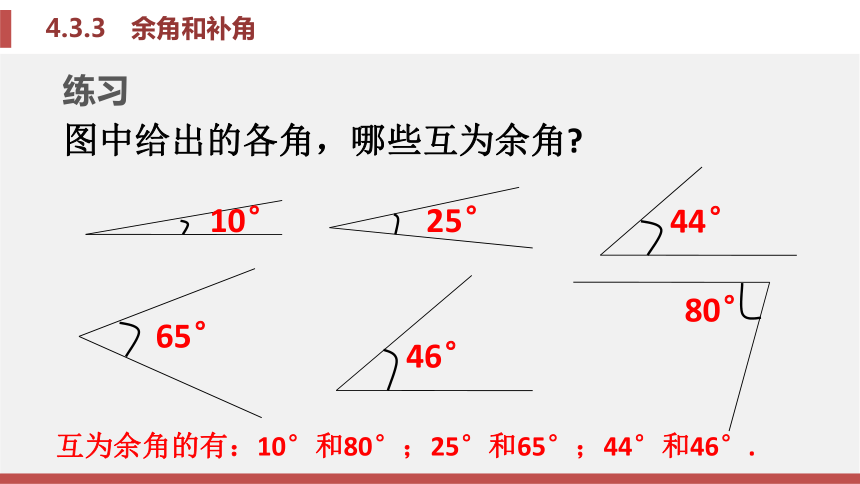
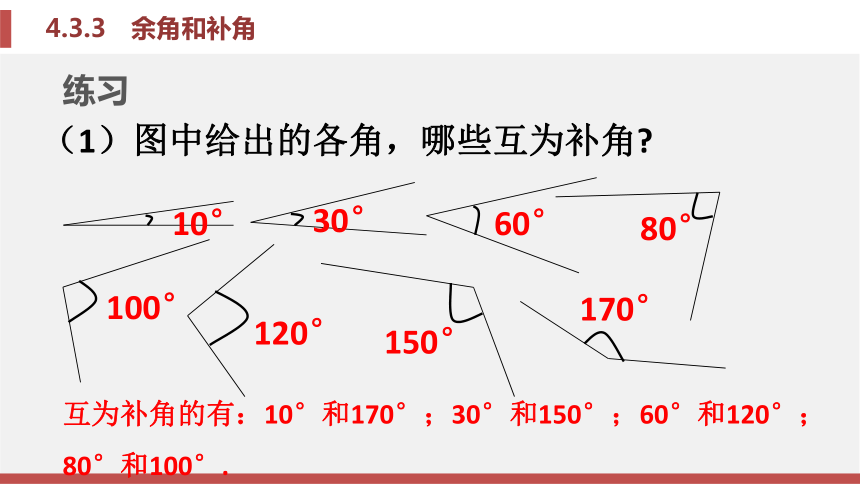
它现在与地面成的夹角约是86.03°.这两个角之和是多少?如果两个角的和等于90°(直角),那么就说这两个角互为余角,即其中一个角是另一个角的余角,即若∠1十∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角. 练习互为余角的有:10°和80°;25°和65°;44°和46°.如果两个角的和等于180°(平角),那么就说这两个角互为补角,即其中一个角是另一个角的补角.即若∠3十∠4=180°,那么∠3是∠ 4的补角,∠ 4也是∠3的补角.练习互为补角的有:10°和170°;30°和150°;60°和120°;80°和100°.(2)填下表.85°135°45°148°175°58°(180-x)°(90- x )°117°37 ′27°37 ′ 103° 13°结论:同一锐角的补角比它的余角大90°.(3)填空
①70°的余角是 ,补角是 .
② ∠α( ∠α<90°)的余角是 ,它的补角是 .20°110°90°-α180°-α(4)思考:∠1与∠2,∠3都互为补角,∠2
和∠3的大小有什么关系?如果∠1与∠2,∠3
都互为余角,∠2和∠3的大小又有什么关系?结论:∠1与∠2,∠3都互为补角,那么∠2=180°-∠1,∠3=180°-∠1,从而∠2=∠3.
∠1与∠2,∠3都互为余角,那么∠2=90°-∠1,∠3=90°-∠1,从而∠2=∠3.补角性质:同角(或等角)的补角相等.
余角性质:同角(或等角)的余角相等.有时以正北、正南方向为基准,描述物体运动的方向.表示方向的角(方位角)在航行、测绘等工作中经常用到. 方位的表示通常用“北偏东多少度”“北偏西多少度”或者“南偏东多少度”“南偏西多少度”来表示.“北偏东45°”“北偏西45°”或者“南偏东45°”“南偏西45°”,分别称为“东北方向”
“西北方向”“东南方向”“西南方向”.画法:以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.同理,可以画出表示货轮C和海岛D方向的射线.● A60°40° B C10°45° D谢 谢 观 看!
它现在与地面成多少度角?倾斜了约3.97°.
它现在与地面成的夹角约是86.03°.这两个角之和是多少?如果两个角的和等于90°(直角),那么就说这两个角互为余角,即其中一个角是另一个角的余角,即若∠1十∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角. 练习互为余角的有:10°和80°;25°和65°;44°和46°.如果两个角的和等于180°(平角),那么就说这两个角互为补角,即其中一个角是另一个角的补角.即若∠3十∠4=180°,那么∠3是∠ 4的补角,∠ 4也是∠3的补角.练习互为补角的有:10°和170°;30°和150°;60°和120°;80°和100°.(2)填下表.85°135°45°148°175°58°(180-x)°(90- x )°117°37 ′27°37 ′ 103° 13°结论:同一锐角的补角比它的余角大90°.(3)填空
①70°的余角是 ,补角是 .
② ∠α( ∠α<90°)的余角是 ,它的补角是 .20°110°90°-α180°-α(4)思考:∠1与∠2,∠3都互为补角,∠2
和∠3的大小有什么关系?如果∠1与∠2,∠3
都互为余角,∠2和∠3的大小又有什么关系?结论:∠1与∠2,∠3都互为补角,那么∠2=180°-∠1,∠3=180°-∠1,从而∠2=∠3.
∠1与∠2,∠3都互为余角,那么∠2=90°-∠1,∠3=90°-∠1,从而∠2=∠3.补角性质:同角(或等角)的补角相等.
余角性质:同角(或等角)的余角相等.有时以正北、正南方向为基准,描述物体运动的方向.表示方向的角(方位角)在航行、测绘等工作中经常用到. 方位的表示通常用“北偏东多少度”“北偏西多少度”或者“南偏东多少度”“南偏西多少度”来表示.“北偏东45°”“北偏西45°”或者“南偏东45°”“南偏西45°”,分别称为“东北方向”
“西北方向”“东南方向”“西南方向”.画法:以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.同理,可以画出表示货轮C和海岛D方向的射线.● A60°40° B C10°45° D谢 谢 观 看!
