人教版七年级数学上册第三章一元一次方程3.2第2课时用移项、合并同类项解一元一次方程课件(共19张)
文档属性
| 名称 | 人教版七年级数学上册第三章一元一次方程3.2第2课时用移项、合并同类项解一元一次方程课件(共19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 461.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-30 00:00:00 | ||
图片预览





文档简介
课件19张PPT。 “复兴号”高铁的速度是350 km/h,北京、上海两地相距1318 km,需要行驶 x 小时,则
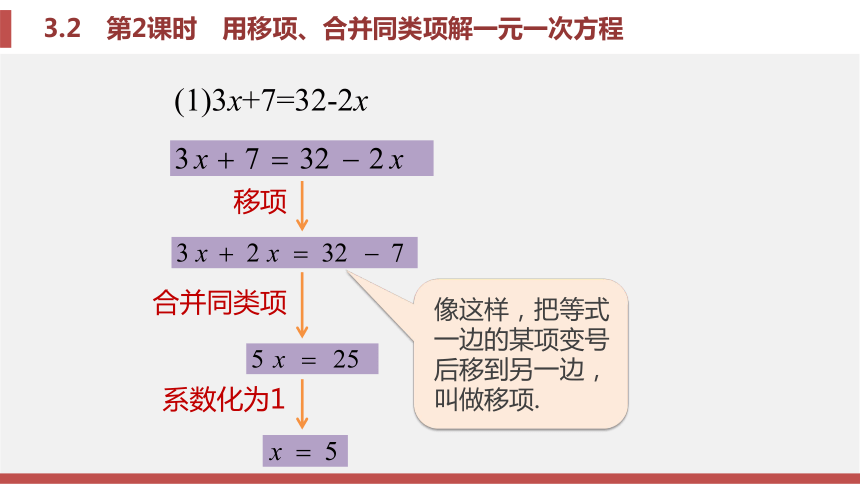
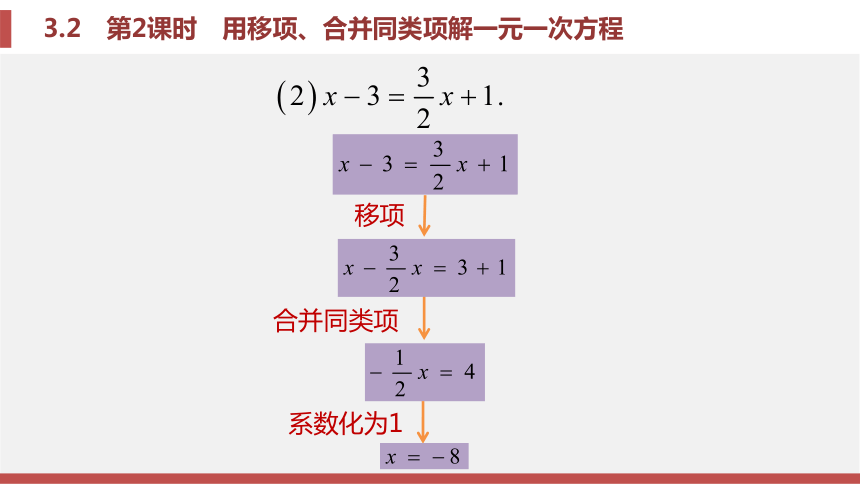
350x = 13183.2 第2课时 用移项、合并同类项解一元一次方程 上节课我们介绍了中亚西亚数学家阿尔—花拉子米写了一本代数书,它重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》,“对消”与“还原”是什么意思呢?哪位同学来说一说?3.2 第2课时 用移项、合并同类项解一元一次方程对消:顾名思义,就是将方程中各项成对消除的意思,相当于现代解方程中的“合并同类项”.还原:就是把方程转换成左边各项都含有未知数,右边各项都不含未知数的形式,相当于现代解方程中的“移项”.3.2 第2课时 用移项、合并同类项解一元一次方程例3 解下列方程:分析:怎样解这两个方程,如何使它向x=a转化?化归的思想3.2 第2课时 用移项、合并同类项解一元一次方程合并同类项系数化为1移项(1)3x+7=32-2x3.2 第2课时 用移项、合并同类项解一元一次方程系数化为1,得x=5.解:移项,得合并同类项,得请根据上面的步骤完成(2)的解答.(1)3x+7=32-2x;3.2 第2课时 用移项、合并同类项解一元一次方程合并同类项系数化为1移项3.2 第2课时 用移项、合并同类项解一元一次方程系数化为1,得 x=-8解:移项,得合并同类项,得3.2 第2课时 用移项、合并同类项解一元一次方程问题2 把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?思考:(1)你认为题中涉及哪些数量关系和相等关系?(2)你认为引进什么样的未知数,根据这样的相等关系列出方程?3.2 第2课时 用移项、合并同类项解一元一次方程分析:设这个班学生有x人.(1)每人分3本,共分出 本,加上剩余20本,
这批书共有 本. (2)每人分4本,需要 本,减去缺的25本,
这批书共有 本.3x4x(3x+20)(4x-25)3.2 第2课时 用移项、合并同类项解一元一次方程表示同一个量的两个不同的式子相等相等关系是: .这批书的总数是一个定值列得方程: .3x+20=4x-253.2 第2课时 用移项、合并同类项解一元一次方程解:依题意,可列方程3x +20=4x -25.系数化为1,得 x =45.移项,得3x -4x =-25-20.合并同类项,得-x =-45.答:这个班有45名学生.3.2 第2课时 用移项、合并同类项解一元一次方程例3 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少? 思考:(1)你准备设哪个未知数?
(2)你能在问题中把表示等量关系的语句
找出来,并用等式进行表示吗?3.2 第2课时 用移项、合并同类项解一元一次方程 等号两边代表
哪个数量?解:设新、旧工艺的废水排量分别为2x t和5x t.根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100移项,得
5x-2x=100+200 合并同类项,得
3x=300 系数化为1,得
x=100 所以 2x=200,
5x=500. 答:新旧工艺产生的废水数量分别为200 t和500 t.3.2 第2课时 用移项、合并同类项解一元一次方程练习 1.解下列方程:3.2 第2课时 用移项、合并同类项解一元一次方程系数化为1,得 x=1解:移项,得合并同类项,得3.2 第2课时 用移项、合并同类项解一元一次方程系数化为1,得 x=-24解:移项,得合并同类项,得3.2 第2课时 用移项、合并同类项解一元一次方程拓展
甲、乙两个商场搞促销活动,甲商场的活动为所有商品全部按标价的8折出售,乙商场的活动为标价200元以下的商品按标价出售,超出200元的部分打7折.现有某件商品在两个商场的标价都为400元,应当在哪个商场购买更实惠?如果标价为600元呢?为800元呢?你能否给顾客一些建议,以便获得更大的实惠呢?谢 谢 观 看!
350x = 13183.2 第2课时 用移项、合并同类项解一元一次方程 上节课我们介绍了中亚西亚数学家阿尔—花拉子米写了一本代数书,它重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》,“对消”与“还原”是什么意思呢?哪位同学来说一说?3.2 第2课时 用移项、合并同类项解一元一次方程对消:顾名思义,就是将方程中各项成对消除的意思,相当于现代解方程中的“合并同类项”.还原:就是把方程转换成左边各项都含有未知数,右边各项都不含未知数的形式,相当于现代解方程中的“移项”.3.2 第2课时 用移项、合并同类项解一元一次方程例3 解下列方程:分析:怎样解这两个方程,如何使它向x=a转化?化归的思想3.2 第2课时 用移项、合并同类项解一元一次方程合并同类项系数化为1移项(1)3x+7=32-2x3.2 第2课时 用移项、合并同类项解一元一次方程系数化为1,得x=5.解:移项,得合并同类项,得请根据上面的步骤完成(2)的解答.(1)3x+7=32-2x;3.2 第2课时 用移项、合并同类项解一元一次方程合并同类项系数化为1移项3.2 第2课时 用移项、合并同类项解一元一次方程系数化为1,得 x=-8解:移项,得合并同类项,得3.2 第2课时 用移项、合并同类项解一元一次方程问题2 把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?思考:(1)你认为题中涉及哪些数量关系和相等关系?(2)你认为引进什么样的未知数,根据这样的相等关系列出方程?3.2 第2课时 用移项、合并同类项解一元一次方程分析:设这个班学生有x人.(1)每人分3本,共分出 本,加上剩余20本,
这批书共有 本. (2)每人分4本,需要 本,减去缺的25本,
这批书共有 本.3x4x(3x+20)(4x-25)3.2 第2课时 用移项、合并同类项解一元一次方程表示同一个量的两个不同的式子相等相等关系是: .这批书的总数是一个定值列得方程: .3x+20=4x-253.2 第2课时 用移项、合并同类项解一元一次方程解:依题意,可列方程3x +20=4x -25.系数化为1,得 x =45.移项,得3x -4x =-25-20.合并同类项,得-x =-45.答:这个班有45名学生.3.2 第2课时 用移项、合并同类项解一元一次方程例3 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少? 思考:(1)你准备设哪个未知数?
(2)你能在问题中把表示等量关系的语句
找出来,并用等式进行表示吗?3.2 第2课时 用移项、合并同类项解一元一次方程 等号两边代表
哪个数量?解:设新、旧工艺的废水排量分别为2x t和5x t.根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100移项,得
5x-2x=100+200 合并同类项,得
3x=300 系数化为1,得
x=100 所以 2x=200,
5x=500. 答:新旧工艺产生的废水数量分别为200 t和500 t.3.2 第2课时 用移项、合并同类项解一元一次方程练习 1.解下列方程:3.2 第2课时 用移项、合并同类项解一元一次方程系数化为1,得 x=1解:移项,得合并同类项,得3.2 第2课时 用移项、合并同类项解一元一次方程系数化为1,得 x=-24解:移项,得合并同类项,得3.2 第2课时 用移项、合并同类项解一元一次方程拓展
甲、乙两个商场搞促销活动,甲商场的活动为所有商品全部按标价的8折出售,乙商场的活动为标价200元以下的商品按标价出售,超出200元的部分打7折.现有某件商品在两个商场的标价都为400元,应当在哪个商场购买更实惠?如果标价为600元呢?为800元呢?你能否给顾客一些建议,以便获得更大的实惠呢?谢 谢 观 看!
