人教版七年级数学上册第三章一元一次方程3.4第3课时比赛、分段计费问题与一元一次方程课件(共28张)
文档属性
| 名称 | 人教版七年级数学上册第三章一元一次方程3.4第3课时比赛、分段计费问题与一元一次方程课件(共28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 737.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-30 00:00:00 | ||
图片预览







文档简介
课件28张PPT。 “复兴号”高铁的速度是350 km/h,北京、上海两地相距1318 km,需要行驶 x 小时,则
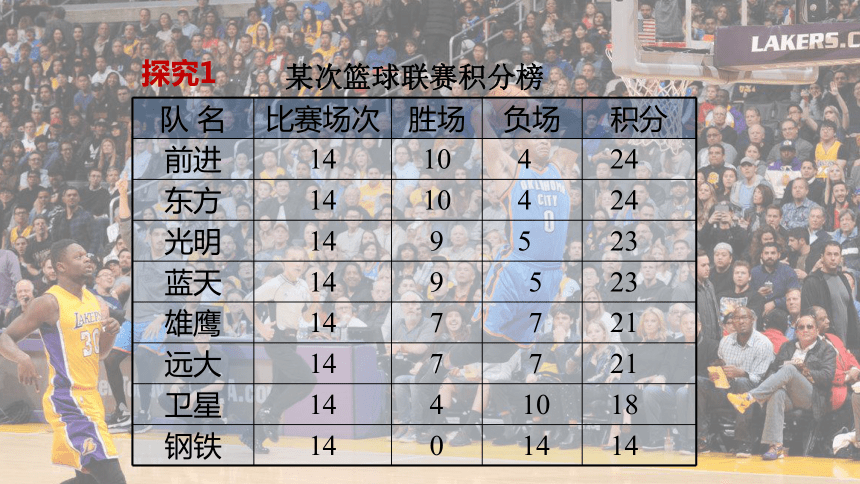
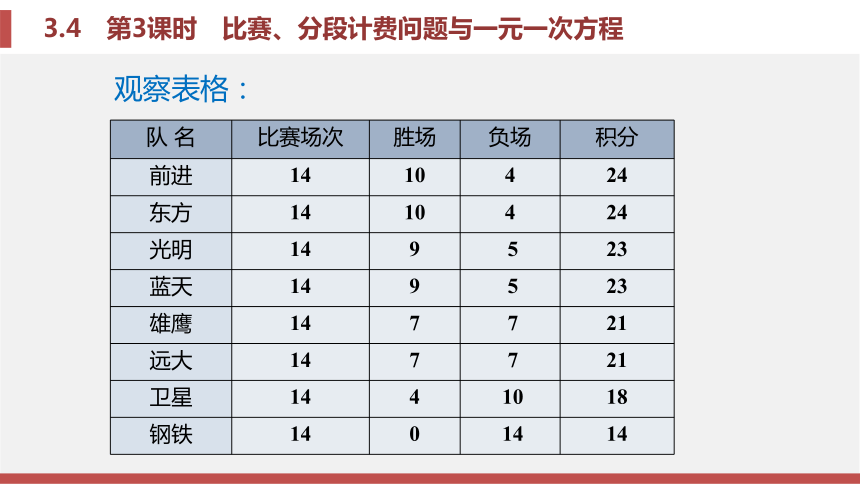
350x = 1318探究1某次篮球联赛积分榜3.4 第3课时 比赛、分段计费问题与一元一次方程(2)某队的胜场总积分能等于它的负场总积分吗?(1)用式子表示总积分与胜、负场数之间的数量关系;解决问题的关键:胜一场积几分,负一场积几分.胜场积分+负场积分=总积分3.4 第3课时 比赛、分段计费问题与一元一次方程观察表格:3.4 第3课时 比赛、分段计费问题与一元一次方程问题1:你选择表格中哪一行能说明负一场积几分呢?最后一行负一场积1分3.4 第3课时 比赛、分段计费问题与一元一次方程问题2:那胜一场积多少分呢?胜一场积2分结论:负一场积1分,胜一场积2分.3.4 第3课时 比赛、分段计费问题与一元一次方程解:若一个队胜m场,则负(14-m)场,总积分为 2m+(14–m) = m+14.即胜m场的总积分为(m +14)分.(1)用式子表示总积分与胜、负场数之间的数量关系;3.4 第3课时 比赛、分段计费问题与一元一次方程(2)某队的胜场总积分能等于它的负场总积分吗?解:设一个队胜了x场,则负了(14-x)场.根据题意,得 2x=14-x.解得x=3.4 第3课时 比赛、分段计费问题与一元一次方程解决实际问题时,要考虑得到的结果是不是符合实际 其中,x (所胜的场数)的值必须是整数,所以 x= 不符合实际.由此可以判定没有哪个队伍的胜场总积分等于负场总积分. 注意:①负场数=比赛场数-胜场数②总积分=胜场积分+负场积分3.4 第3课时 比赛、分段计费问题与一元一次方程思考:如果删去积分表的最后一行,你还能解决这两个问题吗?3.4 第3课时 比赛、分段计费问题与一元一次方程提示:可利用各队胜一场积分相等或利用各队负一场积分相等,任选两个胜、负场数不同的球队列方程解决.3.4 第3课时 比赛、分段计费问题与一元一次方程探究2 下表中有两种移动电话计费方式,请你帮忙计算一下哪种方式更省钱.3.4 第3课时 比赛、分段计费问题与一元一次方程(1)设一个月内用移动电话主叫为t min(t为正整数).根据上表,列表说明:当在不同时间范围内取值时,按方式一和方式二如何计费.(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.考虑下列问题:分 析35001503.4 第3课时 比赛、分段计费问题与一元一次方程营业厅根据 的不同进行收费,所以我们可以根据主叫限定时间进行分情况讨论,把____和____作为不同时间范围的划分点,可以分为几种情况:主叫时间150350(1)t<150(2)t=150(3)150<t<350(4)t=350(5)t>3503.4 第3课时 比赛、分段计费问题与一元一次方程(1)当t取不同范围内的值时,方式一和方式二的计费如下表:585858+0.25(t-150)10858+0.25(t-150)8888888888+0.19(t-350)3.4 第3课时 比赛、分段计费问题与一元一次方程(2)观察上表,可以看出:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.①从表格中,可以看出当t≤150时,按方式一的计费少.②当t从150增加到350时,按方式一的计费由58元增加到108元,而方式二的计费一直是88元,所以方式一在变化过程中,可能在某一主叫时间,两种方式计费相等.3.4 第3课时 比赛、分段计费问题与一元一次方程列方程58+0.25(t-150)=88.
解得t=270.故当 t =270时,两种计费方式的费用相同,都是88元;当150当270270 min时,选择方案二省钱;当t=270 min时,选择方案一和方案二一样.根据以上分析,可以发现3.4 第3课时 比赛、分段计费问题与一元一次方程练习 某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价40元,乒乓球每盒10元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需买球拍6副,乒乓球若干盒(不小于6盒).3.4 第3课时 比赛、分段计费问题与一元一次方程(1)当购买多少盒乒乓球时,两种优惠办法 付款一样?
(2)当购买20盒乒乓球时,请你去办这件事,你打算去哪
家商店购买?为什么? (3)当购买40盒乒乓球时,请你去办这件事, 你打算去哪
家商店购买?为什么?3.4 第3课时 比赛、分段计费问题与一元一次方程解:(1)设当购买乒乓球x盒时,两种优惠办法付款一样.根据题意,得
40 × 6+10(x -6)=(40×6+10x)×90%.解得x=36.答:当购买36盒乒乓球时,两种优惠办法付款一样.3.4 第3课时 比赛、分段计费问题与一元一次方程(2)当购买20盒乒乓球时,去甲商店需付款:
40×6+10× (20-6)=380(元)去乙商店需付款:
(40×6+10×20) ×90%=396(元)因为380元<396元,所以当购买20盒乒乓球时, 去甲商店购买划算.3.4 第3课时 比赛、分段计费问题与一元一次方程(3)当购买40盒乒乓球时,去甲商店需付款:
40 × 6+10(40-6)= 580(元)去乙商店需付款:
(40×6+10×40)×90%=576(元)因为576元<580元,所以当购买40盒乒乓球时, 去乙商店购买划算.3.4 第3课时 比赛、分段计费问题与一元一次方程小 结谢 谢 观 看!
350x = 1318探究1某次篮球联赛积分榜3.4 第3课时 比赛、分段计费问题与一元一次方程(2)某队的胜场总积分能等于它的负场总积分吗?(1)用式子表示总积分与胜、负场数之间的数量关系;解决问题的关键:胜一场积几分,负一场积几分.胜场积分+负场积分=总积分3.4 第3课时 比赛、分段计费问题与一元一次方程观察表格:3.4 第3课时 比赛、分段计费问题与一元一次方程问题1:你选择表格中哪一行能说明负一场积几分呢?最后一行负一场积1分3.4 第3课时 比赛、分段计费问题与一元一次方程问题2:那胜一场积多少分呢?胜一场积2分结论:负一场积1分,胜一场积2分.3.4 第3课时 比赛、分段计费问题与一元一次方程解:若一个队胜m场,则负(14-m)场,总积分为 2m+(14–m) = m+14.即胜m场的总积分为(m +14)分.(1)用式子表示总积分与胜、负场数之间的数量关系;3.4 第3课时 比赛、分段计费问题与一元一次方程(2)某队的胜场总积分能等于它的负场总积分吗?解:设一个队胜了x场,则负了(14-x)场.根据题意,得 2x=14-x.解得x=3.4 第3课时 比赛、分段计费问题与一元一次方程解决实际问题时,要考虑得到的结果是不是符合实际 其中,x (所胜的场数)的值必须是整数,所以 x= 不符合实际.由此可以判定没有哪个队伍的胜场总积分等于负场总积分. 注意:①负场数=比赛场数-胜场数②总积分=胜场积分+负场积分3.4 第3课时 比赛、分段计费问题与一元一次方程思考:如果删去积分表的最后一行,你还能解决这两个问题吗?3.4 第3课时 比赛、分段计费问题与一元一次方程提示:可利用各队胜一场积分相等或利用各队负一场积分相等,任选两个胜、负场数不同的球队列方程解决.3.4 第3课时 比赛、分段计费问题与一元一次方程探究2 下表中有两种移动电话计费方式,请你帮忙计算一下哪种方式更省钱.3.4 第3课时 比赛、分段计费问题与一元一次方程(1)设一个月内用移动电话主叫为t min(t为正整数).根据上表,列表说明:当在不同时间范围内取值时,按方式一和方式二如何计费.(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.考虑下列问题:分 析35001503.4 第3课时 比赛、分段计费问题与一元一次方程营业厅根据 的不同进行收费,所以我们可以根据主叫限定时间进行分情况讨论,把____和____作为不同时间范围的划分点,可以分为几种情况:主叫时间150350(1)t<150(2)t=150(3)150<t<350(4)t=350(5)t>3503.4 第3课时 比赛、分段计费问题与一元一次方程(1)当t取不同范围内的值时,方式一和方式二的计费如下表:585858+0.25(t-150)10858+0.25(t-150)8888888888+0.19(t-350)3.4 第3课时 比赛、分段计费问题与一元一次方程(2)观察上表,可以看出:主叫时间超出限定时间越长,计费越多,并且随着主叫时间的变化,按哪种方式的计费少也会变化.①从表格中,可以看出当t≤150时,按方式一的计费少.②当t从150增加到350时,按方式一的计费由58元增加到108元,而方式二的计费一直是88元,所以方式一在变化过程中,可能在某一主叫时间,两种方式计费相等.3.4 第3课时 比赛、分段计费问题与一元一次方程列方程58+0.25(t-150)=88.
解得t=270.故当 t =270时,两种计费方式的费用相同,都是88元;当150
家商店购买?为什么? (3)当购买40盒乒乓球时,请你去办这件事, 你打算去哪
家商店购买?为什么?3.4 第3课时 比赛、分段计费问题与一元一次方程解:(1)设当购买乒乓球x盒时,两种优惠办法付款一样.根据题意,得
40 × 6+10(x -6)=(40×6+10x)×90%.解得x=36.答:当购买36盒乒乓球时,两种优惠办法付款一样.3.4 第3课时 比赛、分段计费问题与一元一次方程(2)当购买20盒乒乓球时,去甲商店需付款:
40×6+10× (20-6)=380(元)去乙商店需付款:
(40×6+10×20) ×90%=396(元)因为380元<396元,所以当购买20盒乒乓球时, 去甲商店购买划算.3.4 第3课时 比赛、分段计费问题与一元一次方程(3)当购买40盒乒乓球时,去甲商店需付款:
40 × 6+10(40-6)= 580(元)去乙商店需付款:
(40×6+10×40)×90%=576(元)因为576元<580元,所以当购买40盒乒乓球时, 去乙商店购买划算.3.4 第3课时 比赛、分段计费问题与一元一次方程小 结谢 谢 观 看!
