2018-2019学年七年级数学下册9.4平行线的判定作业设计含答案
文档属性
| 名称 | 2018-2019学年七年级数学下册9.4平行线的判定作业设计含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 47.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-30 14:16:59 | ||
图片预览


文档简介
9.4 平行线的判定
一.选择题:
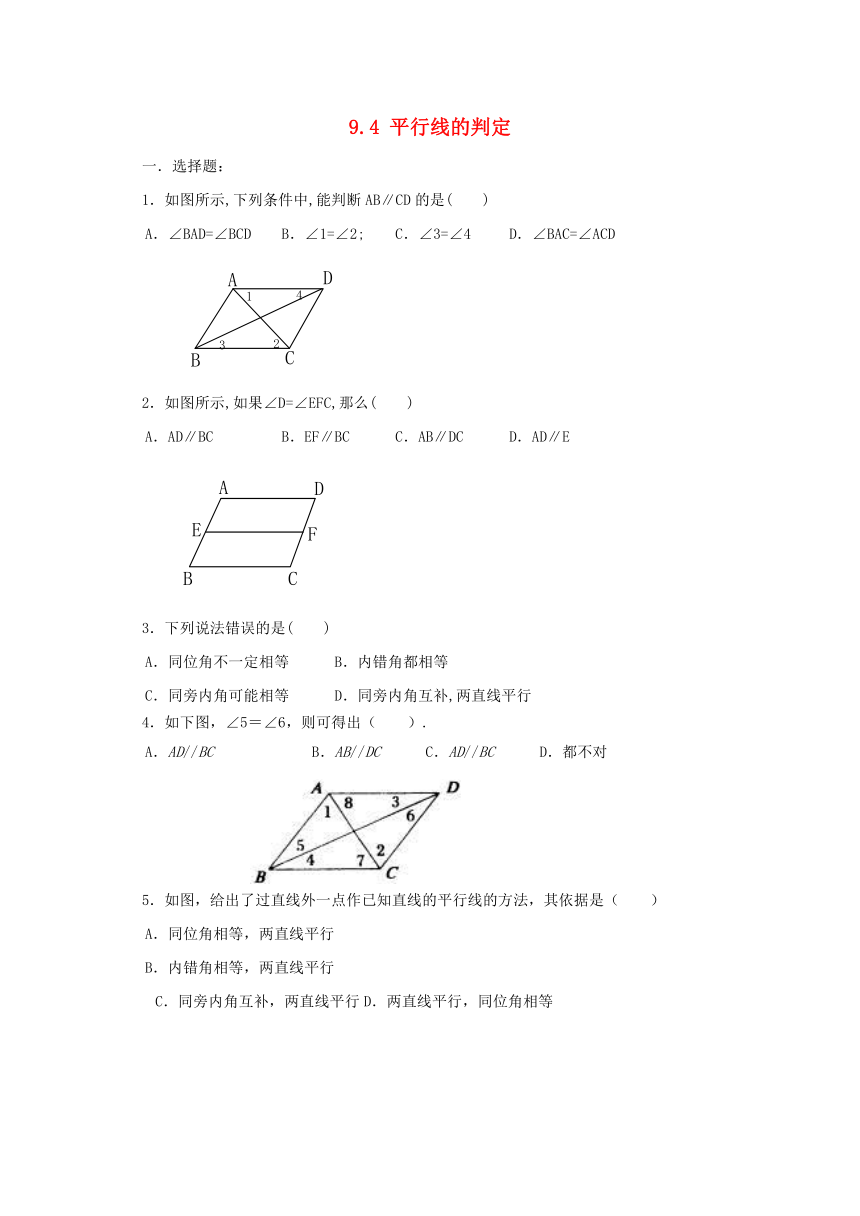
1.如图所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
2.如图所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥E
3.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
4.如下图,∠5=∠6,则可得出( ).
A.AD//BC???? B.AB//DC C.AD//BC ? D.都不对
5.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行D.两直线平行,同位角相等
二.填空题:
6.在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是______.
7.如图,完成下列填空:
①如果∠1=∠C,可得ED∥ ,依据是 .
②如果∠2=∠BED,可得DF∥ ,依据是 .
③如果∠BED=∠A,可得 ,依据是 .
8.填空题(1)如图
∵ (已知),
∴____∥____,理由是(? ?? )
又∵ (已知)
∴_______=,理由是(?? ? ??)
∴_____∥______,理由是(??? ??)
三.解答题:
9.如图所示,已知∠1=∠2,AB平分∠DAB,试说明DC∥AB.
10.如图,AD是一条直线, . .
说明:BE∥CF.
11.如图, ,. 说明:AB∥CD.
参考答案
1.解:选D
2.解:选D
3.解: 选B
4.解:选B
5.解:选A
6.解:相交
7.解:①FC同位角相等,两直线平行②BE 内错角相等,两直线平行③ED∥AC 同位角相等,两直线平行
8.解:AE BD 内错角相等,两直线平行;∠2 ;等量代换;AC ED 同位角相等,两直线平行
9.解:∵AC平分∠DAB,∴∠1=∠CAB,又∵∠1=∠2,∴∠CAB=∠2,∴AB∥CD.
10. 解:∵∠2=115° ∴∠BCF=65° ∴∠1=∠BCF ∴BE ∥CF
11.解:∵∠1=70° ∴∠3=∠1=70°∴ ∠1=∠2=70°∴ AB ∥CD
A
1
B
C
F
E
2
3
D
PAGE
一.选择题:
1.如图所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
2.如图所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥E
3.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
4.如下图,∠5=∠6,则可得出( ).
A.AD//BC???? B.AB//DC C.AD//BC ? D.都不对
5.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行D.两直线平行,同位角相等
二.填空题:
6.在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是______.
7.如图,完成下列填空:
①如果∠1=∠C,可得ED∥ ,依据是 .
②如果∠2=∠BED,可得DF∥ ,依据是 .
③如果∠BED=∠A,可得 ,依据是 .
8.填空题(1)如图
∵ (已知),
∴____∥____,理由是(? ?? )
又∵ (已知)
∴_______=,理由是(?? ? ??)
∴_____∥______,理由是(??? ??)
三.解答题:
9.如图所示,已知∠1=∠2,AB平分∠DAB,试说明DC∥AB.
10.如图,AD是一条直线, . .
说明:BE∥CF.
11.如图, ,. 说明:AB∥CD.
参考答案
1.解:选D
2.解:选D
3.解: 选B
4.解:选B
5.解:选A
6.解:相交
7.解:①FC同位角相等,两直线平行②BE 内错角相等,两直线平行③ED∥AC 同位角相等,两直线平行
8.解:AE BD 内错角相等,两直线平行;∠2 ;等量代换;AC ED 同位角相等,两直线平行
9.解:∵AC平分∠DAB,∴∠1=∠CAB,又∵∠1=∠2,∴∠CAB=∠2,∴AB∥CD.
10. 解:∵∠2=115° ∴∠BCF=65° ∴∠1=∠BCF ∴BE ∥CF
11.解:∵∠1=70° ∴∠3=∠1=70°∴ ∠1=∠2=70°∴ AB ∥CD
A
1
B
C
F
E
2
3
D
PAGE
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
