2018学年冀教版七年级数学上册2.3线段的长短作业设计(含解析)
文档属性
| 名称 | 2018学年冀教版七年级数学上册2.3线段的长短作业设计(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 167.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-02 00:00:00 | ||
图片预览




文档简介
2.3 线段的长短
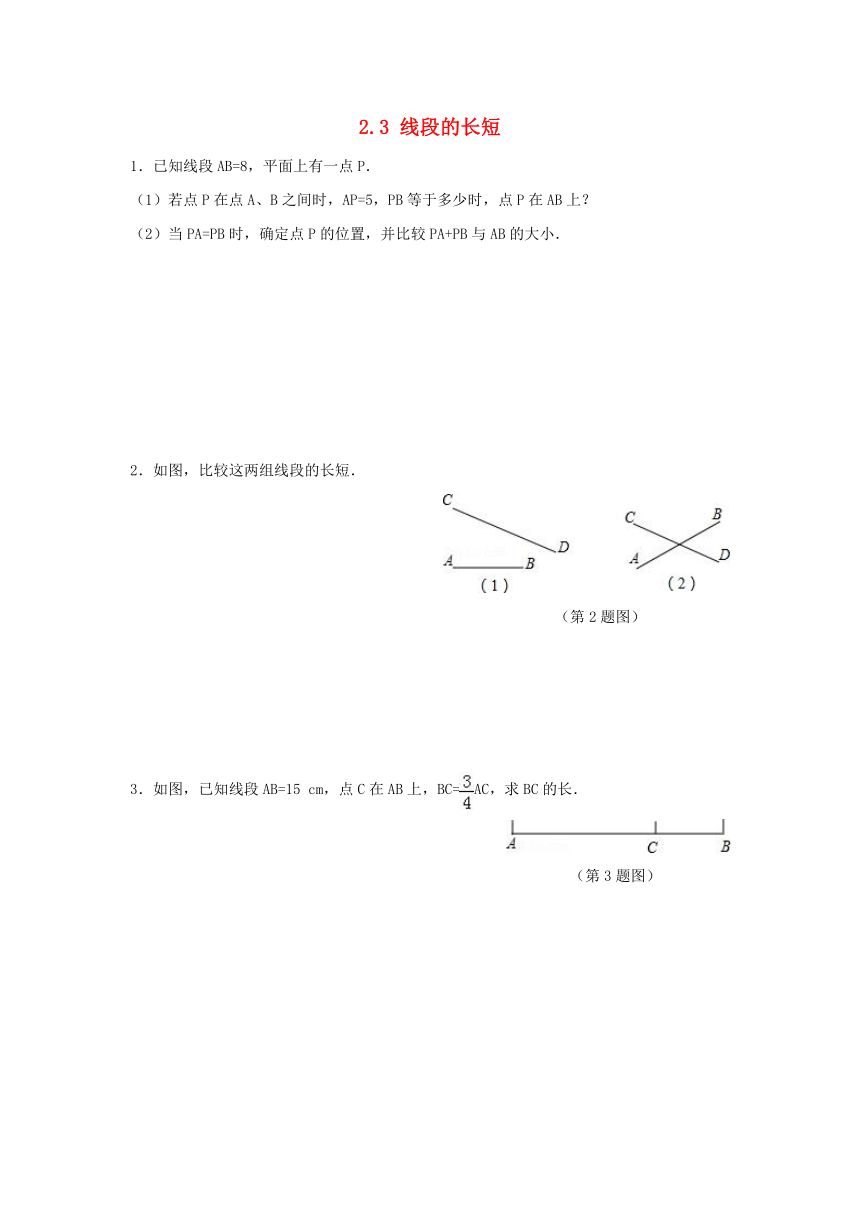
1.已知线段AB=8,平面上有一点P.
(1)若点P在点A、B之间时,AP=5,PB等于多少时,点P在AB上?
(2)当PA=PB时,确定点P的位置,并比较PA+PB与AB的大小.
2.如图,比较这两组线段的长短.
(第2题图)
3.如图,已知线段AB=15 cm,点C在AB上,BC=AC,求BC的长.
(第3题图)
4.如图,C为线段AB的中点,N为线段CB的中点,CN=1cm.求图中线段AC、AN的长度的和为5cm.
(第4题图)
已知线段AB=8厘米,在直线AB上画线段BC=3厘米,求线段AC的长.
点O是线段CD的中点,而点P将CD分为两部分,且CP:PD=,已知线段CD=28cm,求OP的长.
7.如图,AB=6cm,点C是AB的中点,点D是线段AB的六等分点,求CD的长.
(第7题图)
8.如图,M为AB上任一点,C为AM的中点,D为BM的中点,若AB=6,求CD的长.
(第8题图)
9.如图,B,C两点把线段AD分成4:5:7三部分,E是线段AD的中点,CD=14厘米,求:
(1)EC的长;(2)AB:BE的值.
(第9题图)
10.作图题:已知线段a、b、c(a>b>c)
画出满足下列条件的线段:
(1)a﹣b+c;
(2)2a﹣b﹣c;
(3)2(a﹣b)+3(b﹣c).
(第10题图)
11.如图,已知点C在线段AB上,且AC=6 cm,BC=AC,点M,N分别是AC,BC的中点,求线段MN+BN的长度.
(第11题图)
12.如图,AB=20 cm,C是AB上一点,且AC=12 cm,D是AC的中点,E是BC的中点,求线段DE的长.
(第12题图)
13.比较下列各组线段的长短
(1)线段OA与OB.
(2)线段AB与AD.
(3)线段AB、BC与AC.
(1) (2) (3)
(第13题图)
14.如图,已知线段a、b,画线段AB.
(1)画a+b;(2)画2a+b;(3)画2a﹣b.
(第14题图)
参考答案与解析
1.解:(1)3;(2)①当PA=PB时,P在AB的垂直平分线上;
②当P为AB中点时,则AP+PB=AB,利用三角形三边关系得出,此时PA+PB>AB.故PA+PB≥AB.
2.解:(1)把图中的线段AB、线段CD放在一条直线上,使A、C重合,使点D与点B在点A的同侧,点D在线段AB外,所以AB<CD;
(2)把图中的线段AB、线段CD放在一条直线上,使A、C重合,点B和点D重合,所以AB=CD.
3.解:∵AB=15cm,点C在AB上,BC=AC,AC+BC=AB,
∴AC+AC=15,
∴AC==,
∴BC=×=.
4.解:∵N为线段CB的中点,CN=1cm,
∴BC=CN+NB=2(cm).
又∵C为线段AB的中点,
∴AC=BC=2cm,
∴AN=AC+CN=3cm,AC+AN=2+3=5(cm).
5.解:分两种情况:
(1)如答图①.
AC=AB﹣BC=8﹣3=5(厘米);
(2)如答图②.AC=AB+BC=8+3=11(厘米).
① ②
(第5题答图)
答:线段AC的长是5厘米或11厘米.
6.解:∵CP:PD=,CD=28cm,
∴CP=20cm.
又点O是线段CD的中点,
∴CO=14cm,
∴OP=CP﹣CO=6(cm).
7.解:∵AB=6cm,点C是AB的中点,
∴BC=3cm.
∵点D是线段AB的六等分点,
∴BD=1cm,
∴CD=BC﹣BD=3﹣1=2(cm).
8.解:由已知条件可知,AB=6.
∵C为AM的中点,D为MB的中点,
∴CM=AM,DM=BM,
∴CD=CM+DM=AM+BM,
=(AM+BM),
=AB=×6=3.
9.解:设线段AB,BC,CD分别为4x厘米,5x厘米,7x厘米.
∵CD=7x=14,∴x=2.
(1)∵AB=4x=8(厘米),BC=5x=10(厘米),
∴AD=AB+BC+CD=8+10+14=32(厘米),
故EC=AD﹣CD=×32﹣14=2(厘米);
(2)∵BC=10厘米,EC=2厘米,
∴BE=BC﹣EC=10﹣2=8(厘米).
又∵AB=8厘米,
∴AB:BE=8:8=1.
答:EC长是2厘米,AB:BE的值是1.
10.解:所画图形如下答图,其中线段AB即为所求.
(1);
(2)
(3)
(第10题答图)
11.解:∵AC=6cm,
∴BC=AC=4(cm),
∴AB=AC+BC=10(cm).
又∵M、N分别是AC、BC的中点,
∴MN==5(cm),BN=×4=2(cm),
∴MN+BN=7(cm).
12.解:∵AB=20cm,AC=12cm,
∴CB=AB﹣AC=20﹣12=8(cm).
又∵D是AC中点,E是BC中点,
∴DC=AC=×12=6(cm),CE=CB=×8=4(cm),
∴DE=DC+CE=6+4=10(cm).
13.解:(1)OB>OA;
(2)由答图①可知,AD>AB;
(3)由答图②可知,BC>AC>AB.
① ②
(第13题答图)
14.解:(1)如答图①,画线段AC使AC=a,再延长AC至点B,使BC=b,则线段AB即为所求线段;
(2)如答图②,线段AC=2a,BC=b,则线段AB=2a+b;
(3)如答图③,AC=2a,BC=b,则AB=2a﹣b.
① ② ③
(第14题答图)
PAGE
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
