冀教版2018学年七年级数学上册第二章几何图形的初步认识2.6角的大小作业设计含解析
文档属性
| 名称 | 冀教版2018学年七年级数学上册第二章几何图形的初步认识2.6角的大小作业设计含解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-02 00:00:00 | ||
图片预览

文档简介
2.6 角的大小
一.选择题(共10小题)
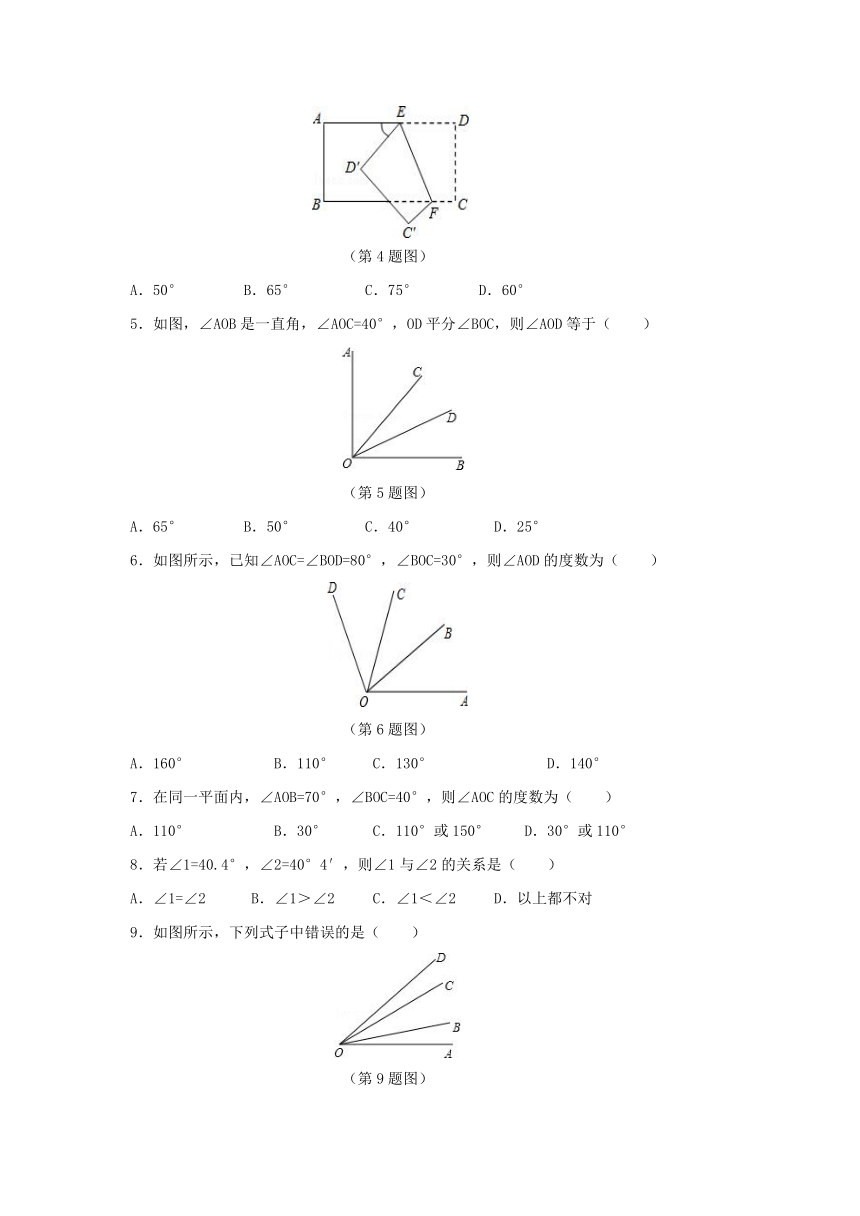
1.如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=( )
(第1题图)
A.90° B.120° C.160° D.180°
2.如图,矩形ABCD沿AE折叠,使点D落在BC边上点F处,如果∠BAF=60°,则∠EAF等于( )
(第2题图)
A.15° B.30° C.45° D.60°
3.如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE,∠COF=34°,则∠BOD的大小为( )
(第3题图)
A.22° B.34° C.56° D.90°
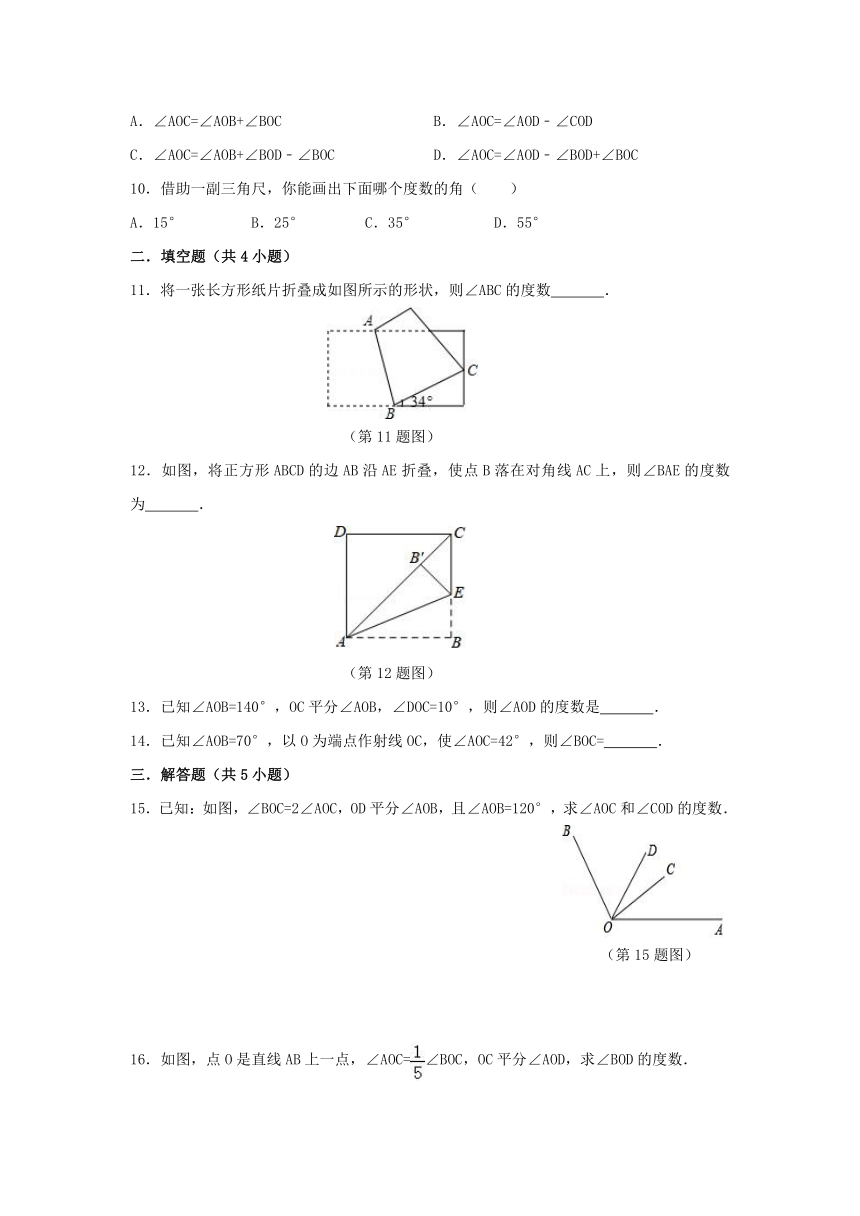
4.如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠AED′=50°,则∠DEF等于( )
(第4题图)
A.50° B.65° C.75° D.60°
5.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于( )
(第5题图)
A.65° B.50° C.40° D.25°
6.如图所示,已知∠AOC=∠BOD=80°,∠BOC=30°,则∠AOD的度数为( )
(第6题图)
A.160° B.110° C.130° D.140°
7.在同一平面内,∠AOB=70°,∠BOC=40°,则∠AOC的度数为( )
A.110° B.30° C.110°或150° D.30°或110°
8.若∠1=40.4°,∠2=40°4′,则∠1与∠2的关系是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.以上都不对
9.如图所示,下列式子中错误的是( )
(第9题图)
A.∠AOC=∠AOB+∠BOC B.∠AOC=∠AOD﹣∠COD
C.∠AOC=∠AOB+∠BOD﹣∠BOC D.∠AOC=∠AOD﹣∠BOD+∠BOC
10.借助一副三角尺,你能画出下面哪个度数的角( )
A.15° B.25° C.35° D.55°
二.填空题(共4小题)
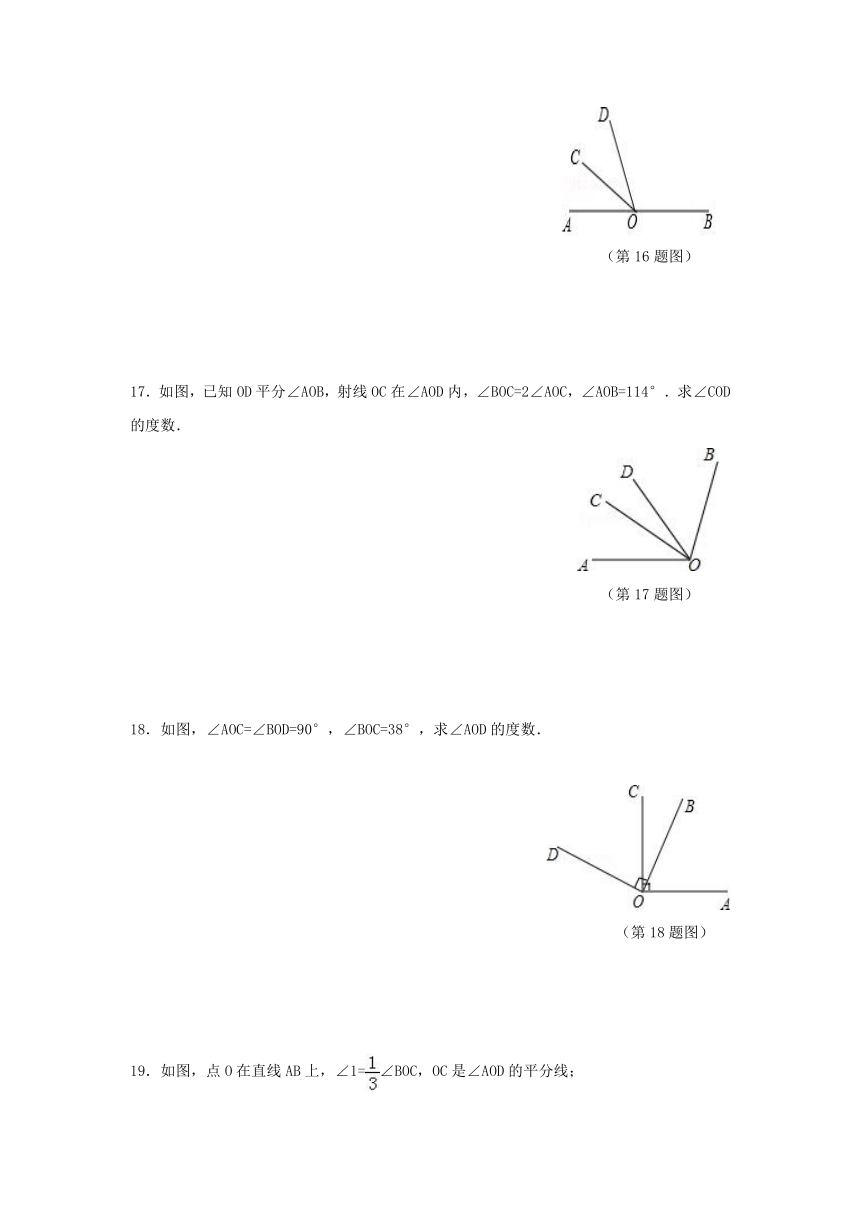
11.将一张长方形纸片折叠成如图所示的形状,则∠ABC的度数 .
(第11题图)
12.如图,将正方形ABCD的边AB沿AE折叠,使点B落在对角线AC上,则∠BAE的度数为 .
(第12题图)
13.已知∠AOB=140°,OC平分∠AOB,∠DOC=10°,则∠AOD的度数是 .
14.已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC= .
三.解答题(共5小题)
15.已知:如图,∠BOC=2∠AOC,OD平分∠AOB,且∠AOB=120°,求∠AOC和∠COD的度数.
(第15题图)
16.如图,点O是直线AB上一点,∠AOC=∠BOC,OC平分∠AOD,求∠BOD的度数.
(第16题图)
17.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°.求∠COD的度数.
(第17题图)
18.如图,∠AOC=∠BOD=90°,∠BOC=38°,求∠AOD的度数.
(第18题图)
19.如图,点O在直线AB上,∠1=∠BOC,OC是∠AOD的平分线;
(1)求:∠2的度数;
(2)试说明:OD⊥AB.
(第19题图)
参考答案与解析
一.1.D【解析】设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,所以∠AOC+∠BOD=90°+a+90°﹣a=180°.故选D.
2.A【解析】∵矩形ABCD中,∠BAD=90°,且∠DAE=∠FAE,∴∠BAF+2∠DAE=90°,∴∠EAF=15°,故选A.
3.A【解析】∵∠COE是直角,∠COF=34°,∴∠EOF=90°﹣34°=56°.∵OF平分∠AOE,
∴∠AOF=∠EOF=56°,∴∠AOC=56°﹣34°=22°,∴∠BOD=∠AOC=22°.故选A.
4.B【解析】∵∠AED′=50°,∴∠DED′=180°﹣∠AED′=180°﹣50°=130°.∵长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,∴∠DEF=∠D′EF,∴∠DEF=∠DED′=×130°=65°.故选B.
5.A【解析】∵∠AOB是一直角,∠AOC=40°,∴∠COB=50°.∵OD平分∠BOC,∴∠COD=25°.∵∠AOD=∠AOC+∠COD,∴∠AOD=65°.故选A.
6.C【解析】∵∠AOC=80°,∠BOC=30°,∴∠AOB=∠AOC﹣∠BOC=80°﹣30°=50°.
又∵∠BOD=80°,∴∠AOD=∠AOB+∠BOD=50°+80°=130°.故选C.
7.D【解析】当OC在∠AOB内时,如答图1所示.∵∠AOB=70°,∠BOC=40°,∴∠AOC=∠AOB﹣∠BOC=30°;当OC在∠AOB外时,如答图2所示.∵∠AOB=70°,∠BOC=40°,∴∠AOC=∠AOB+∠BOC=110°.故选D.
(第7题答图)
8.B【解析】∵∠1=40.4°=40°24′,∠2=40°4′,∴∠1>∠2.故选B.
9.C【解析】A、∠AOC=∠AOB+∠BOC,正确,故本选项错误;B、∠AOC=∠AOD﹣∠COD,正确,故本选项错误;C、∠AOC=∠AOB+∠BOC,∠DOC+∠AOB=∠AOB+∠BOD﹣∠BOC,错误,故本选项正确;D、∠AOC=∠AOD﹣∠BDO+∠BOC,正确,故本选项错误.故选C.
10.A【解析】用一副三角尺,可以画出小于180°的角有:15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,165°.故选A.
二、11.73°【解析】∵∠CBD=34°,∴∠CBE=180°∠CBD=146°,∴∠ABC=∠ABE=∠CBE=73°.
12.22.5°【解析】∵四边形ABCD为正方形,∴∠BAC=45°.由折叠的性质可知,∠BAE=∠B′AE,∴∠BAE=∠BAC=22.5°.
13.60°或80°【解析】分两种情况进行讨论:①如答图1,射线OD在∠AOC的内部.∵OC平分∠AOB,∴∠AOC=∠BOC.∵∠AOB=140°,∴∠AOC=∠BOC=70°.又∵∠COD=10°,∴∠AOD=∠AOC﹣∠COD=60°;②如答图2,射线OD在∠COB的内部.
(第13题答图)
∵OC平分∠AOB,∴∠AOC=∠BOC.∵∠AOB=140°,∴∠AOC=∠BOC=70°.又∵∠C0D=10°,∴∠AOD=∠AOC+∠COD=80°.综上所述,∠AOD=60°或80°.
14.【解析】如图所示,∵∠AOB=70°,∠AOC=42°,∴∠BOC=70°﹣42°=28°,∠BOC′=70°+42°=112°.综上所述∠BOC的度数为112°或28°.
(第14题答图)
三.15.解:设∠AOC=x.∵∠BOC=2∠AOC,∴∠BOC=2x.
∴∠AOB=∠AOC+∠BOC=3x=120°,∴x=40°,∴∠AOC=40°.
∵OD平分∠AOB,∴∠AOD=∠AOB=60°,
∴∠COD=∠AOD﹣∠AOC=20°.
16.解:∵∠AOC+∠BOC=180°,∠AOC=∠COB,∴∠AOC=×180°=30°.
∵OC是∠AOD的平分线,∴∠AOD=2∠AOC=60°,∴∠BOD=180°﹣∠AOD=120°.
解:∵OD平分∠AOB,∠AOB=114°,∴∠AOD=∠BOD==57°.
∵∠BOC=2∠AOC,∠AOB=114°,∴∠AOC=.
∴∠COD=∠AOD﹣∠AOC=57°﹣38°=19°.
18.解:∠AOD=∠AOC+∠BOD﹣∠BOC=90°+90°﹣38°=142°.
19.解:(1)∵∠1=∠BOC,∠1+∠BOC=180°,
∴∠1+3∠1=180°,
解得∠1=45°.
∵OC平分∠AOD,
∴∠2=∠1=45°;
(2)由(1)可得,∠AOD=∠COD+∠AOC=45°+45°=90°,
∴OD⊥AB.
PAGE
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
