冀教版2018学年七年级数学上册第二章几何图形的初步认识2.7角的和与差作业设计含解析
文档属性
| 名称 | 冀教版2018学年七年级数学上册第二章几何图形的初步认识2.7角的和与差作业设计含解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 159.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-02 10:01:14 | ||
图片预览



文档简介
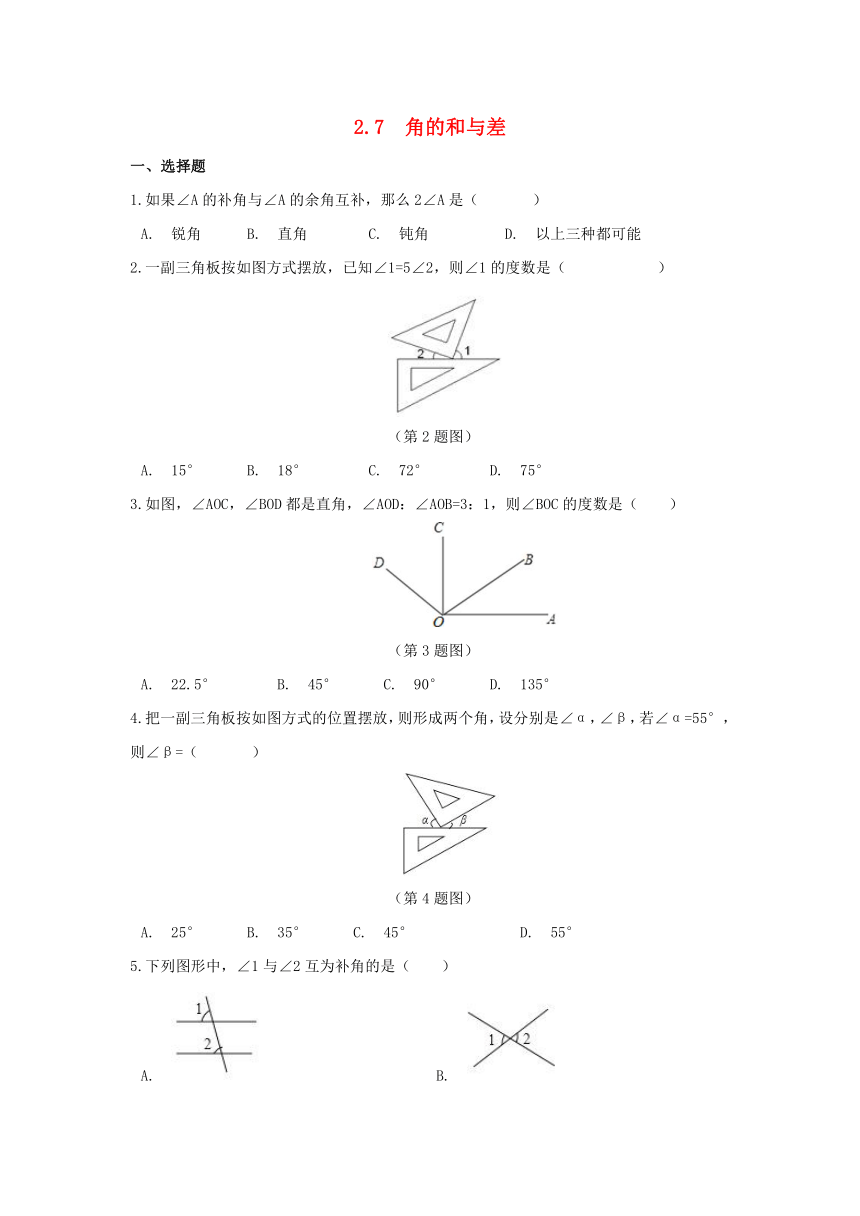
2.7 角的和与差
一、选择题
1.如果∠A的补角与∠A的余角互补,那么2∠A是(?? )
A.?锐角? ?B.?直角????C.?钝角?????D.?以上三种都可能
2.一副三角板按如图方式摆放,已知∠1=5∠2,则∠1的度数是(????? )
(第2题图)
A.?15°???B.?18°????C.?72°????D.?75°
3.如图,∠AOC,∠BOD都是直角,∠AOD:∠AOB=3:1,则∠BOC的度数是( )
?
(第3题图)
A.?22.5°????B.?45° ??C.?90°???D.?135°
4.把一副三角板按如图方式的位置摆放,则形成两个角,设分别是∠α,∠β,若∠α=55°,则∠β=(?? )
(第4题图)
A.?25°???B.?35°???C.?45°???????D.?55°
5.下列图形中,∠1与∠2互为补角的是( )
A.????????????B.?????????????C.???????????D.?
6.如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是(?? )
(第6题图)
?∠ACD=120°???????????? B.?∠ACD=∠BCE??????
?C.?∠ACE=120°??????????? ?D.?∠ACE﹣∠BCD=120°
7.若∠A=34°,则∠A的余角的度数为( )
A.?146°???B.?54°???C.?56°???D.?66°
8.已知∠α和∠β互为余角.若∠α=40°,则∠β等于( )
A.?40°???B.?50°????C.?60°????D.?140°
9.两个锐角的和(? )
A.?必定是锐角????? B.?必定是钝角??????
C.?必定是直角????? D.?可能是锐角,可能是直角,也可能是钝角
如图,已知点O在直线 AB上, ,则 的余角是(???? )
(第10题图)
A.????B.????C.?????D.?
二、填空题
11.如图,图中小于平角的角共有________?个,其中能用一个大写字母表示的角是 ________?.
(第11题图)
12.如果∠1+∠2=90°,而∠2与∠3互余,那么∠1与∠3的数量关系是________.
13.若∠α比60°角的补角的 大35°,则∠α的余角为________°.
14.将一副三角板如图放置,若∠AOD=20°,则∠BOC的大小为________.
(第14题图)
15.已知∠α=40°36′,则∠α的余角为________?.
16.若∠α补角加上30°是∠α余角的3倍,则∠α=________?.
17.若∠A=66°20′,则∠A的余角等于________.?
18.如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB=___度.
(第18题图)
三、解答题
19.一个锐角的补角等于这个锐角的余角的3倍,求这个锐角的度数.
已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.
如图,AO⊥OC,解答下列问题:
①比较∠AOB、∠AOC、∠AOD、∠AOE的大小,并指明其中的锐角、直角、钝角及平角;
②写出∠AOB、∠AOC、∠BOC、∠AOE中某些角之间的两个等量关系.
(第21题图)
22.如图(1)所示,∠AOB、∠COD都是直角.
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示的位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
?
(第22题图)
如图,将书角斜折过去,使角顶点落在A′处,BC为折痕,∠A′BD=∠DBE,求∠CBD的度数.
(第23题图)
参考答案
一、1.B 2.D 3.B 4.B 5.C 6.C 7.C 8.B 9.D 10.A
二、11.7;∠B,∠C 12.相等 13.25 14.160° 15.49°24′ 16.30° 17.23°40′ 18. 180
三、19.解:设这个角的度数为x°,则根据题意,得180﹣x=3(90﹣x),
解得x=45,
即这个锐角为45°.
20.解:设这个角是x,则(180°﹣x)﹣3(90°﹣x)=10°, 解得x=50°.
21.解:(1)∠AOB<∠AOC<∠AOD<∠AOE.
∵AE⊥OC,
∴∠AOC=90°,
∴∠AOB是锐角,∠AOC是直角,∠AOD是钝角,∠AOE是平角;
(2)∠AOB+∠BOC=∠AOC,∠AOB+∠BOC+∠AOC=∠AOE.
22.(1)解:∠AOD与∠COB互补.
理由如下:∵∠AOB、∠COD都是直角,
∴∠AOB=∠COD=90°,
∴∠BOD=∠AOD﹣∠AOB=∠AOD﹣90°,
∠BOD=∠COD﹣∠COB=90°﹣∠COB,
∴∠AOD﹣90°=90°﹣∠COB,
∴∠AOD+∠COB=180°,
∴∠AOD与∠COB互补.
(2)解:成立.
理由如下:∵∠AOB、∠COD都是直角,
∴∠AOB=∠COD=90°.
∵∠AOB+∠BOC+∠COD+∠AOD=360°,
∴∠AOD+∠COB=180°,
∴∠AOD与∠COB互补.
23.解:由题意可知,∠ABC=∠A′BC,∠EBD=∠DBA′, ∴∠CBA′= ∠ABA′,∠A′BD= ∠A′BE,
∴∠CBD=∠CBA′+∠DBA′= (∠A′BA+∠A′BE).
∵∠A′BA+∠A′BE=180°,
∴∠CBD=90°.
PAGE
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
