冀教版2018学年七年级数学上册第二章几何图形的初步认识2.8平面图形的旋转作业设计含解析
文档属性
| 名称 | 冀教版2018学年七年级数学上册第二章几何图形的初步认识2.8平面图形的旋转作业设计含解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 150.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-02 10:04:32 | ||
图片预览


文档简介
2.8 平面图形的旋转
1.(1)计算:+﹣2﹣1;
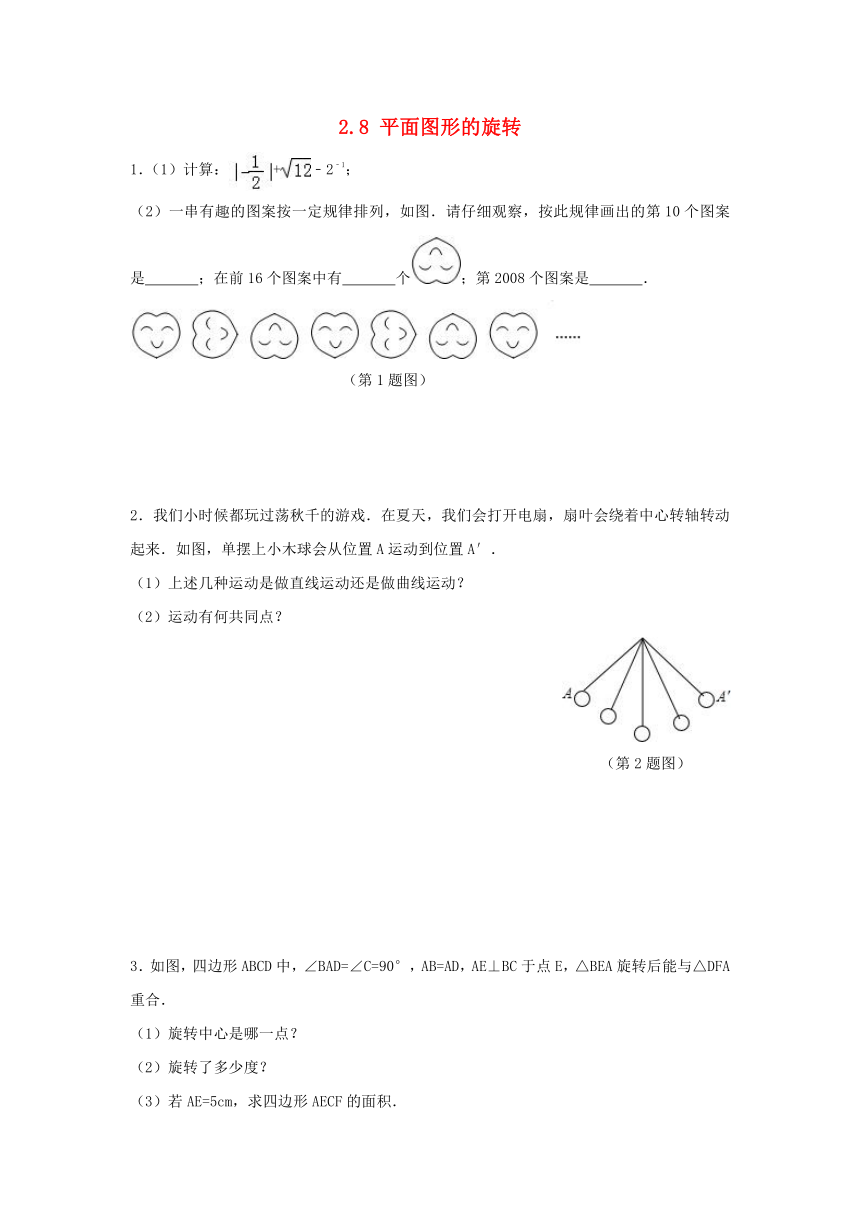
(2)一串有趣的图案按一定规律排列,如图.请仔细观察,按此规律画出的第10个图案是 ;在前16个图案中有 个;第2008个图案是 .
(第1题图)
2.我们小时候都玩过荡秋千的游戏.在夏天,我们会打开电扇,扇叶会绕着中心转轴转动起来.如图,单摆上小木球会从位置A运动到位置A′.
(1)上述几种运动是做直线运动还是做曲线运动?
(2)运动有何共同点?
(第2题图)
3.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于点E,△BEA旋转后能与△DFA重合.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若AE=5cm,求四边形AECF的面积.
(第3题图)
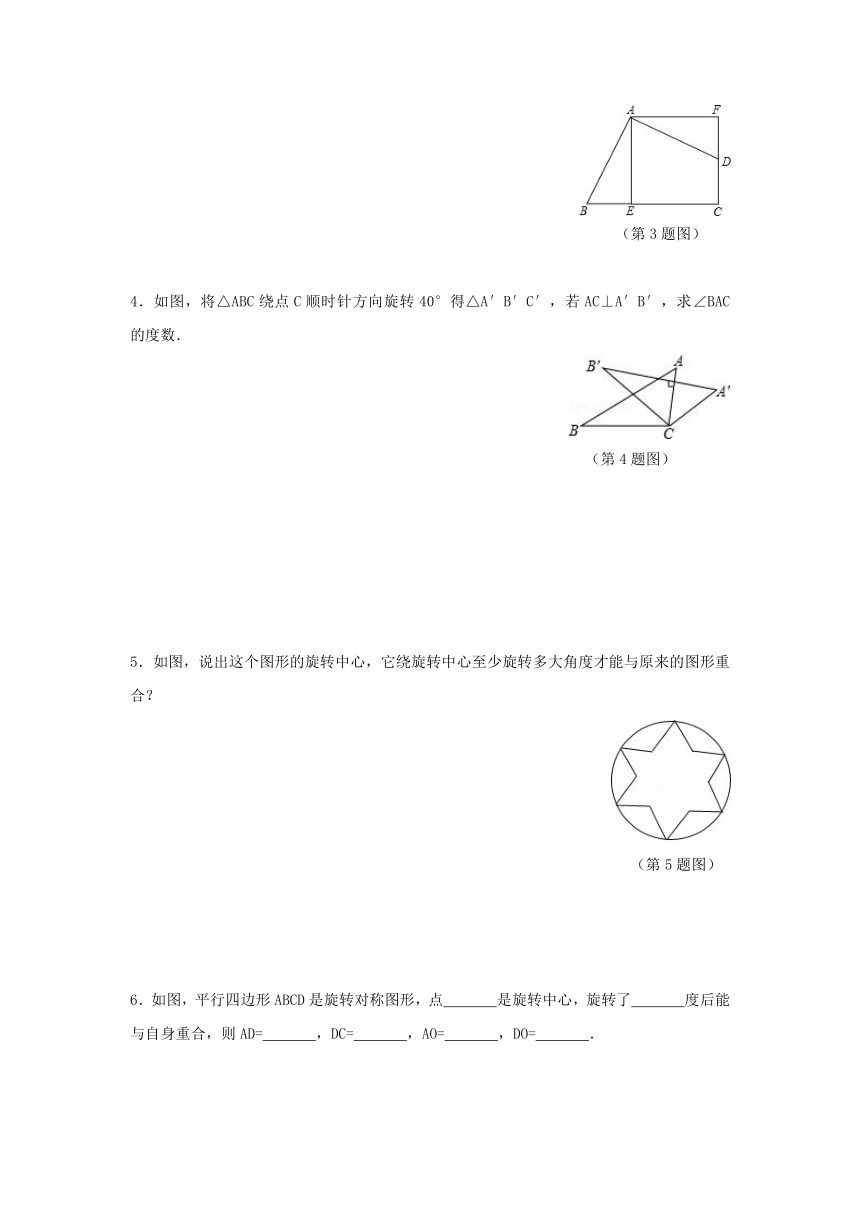
4.如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数.
(第4题图)
5.如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来的图形重合?
(第5题图)
6.如图,平行四边形ABCD是旋转对称图形,点 是旋转中心,旋转了 度后能与自身重合,则AD= ,DC= ,AO= ,DO= .
(第6题图)
7.如图,已知BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是 .
(第7题图)
8.如图,在10×10的正方形网格纸中(每个小方格的边长都是1个单位)有一个△ABC,请在网格纸中画出以点O为旋转中心把△ABC按顺时针方向旋转90°得到的△A′B′C′.
(第8题图)
9.如图,△ABC≌△DFE,AC∥DE,则△ABC经过怎样的变化与△DFE重合?
(第9题图)
10.观察图形由(1)(2)(3)(4)的变化过程,写出每一步图形中各顶点的坐标是如何变化的,图形是如何变化的.
(第10题图)
参考答案与解析
1.解:(1)原式==2;
(2)根据分析,知应分别为,5,.
2.解:(1)上述几种运动是做曲线运动;(2)运动共同点是属于旋转.
3.解:观察:由△BEA到△DFA的旋转过程可知,
(1)点A;
(2)旋转了90度或270度;
(3)由旋转的性质可知,AE=AF,∠F=∠AEB=∠AEC=∠C=90°,
∴四边形AECF是正方形,四边形AECF的面积为AE2=25(cm2).
4.解:∵△ABC绕点C顺时针方向旋转40°得△A′B′C′,
∴∠ACA′=40°,∠A=∠A′.
∵AC⊥A′B′,
∴∠A′=90°﹣40°=50°,
∴∠BAC=50°.
5.解:这个图形的旋转中心为圆心;
∵360°÷6=60°,
∴该图形绕中心至少旋转60度后能和原来的图案互相重合.
6.解:如图平行四边形ABCD是旋转对称图形,点O是旋转中心,旋转了180度后能与自身重合,则AD=BC,DC=AB,AO=OC,DO=OB.
故答案为:O;180,BC;AB;OC;OB.
7.解:如答图.∵△ABC≌△CDE,
∴∠ACB=∠DEC,∠A=∠ECD,
∴∠ACB+∠BCE=90°,
∴∠OFC=∠OGC=∠FCG=90°,
∴∠FOG=90°,
∴旋转角度是90°.
(第7题答图)
8.解:作图如答图.
(第8题答图)
9.解:根据两图形的位置关系可得将△ABC平移使AC与ED重合,
然后以AC的中点为对称中心旋转180°变换即可得到△DFE.
10.解:根据图形和坐标的变化规律可知:
由(1)→(2):纵坐标没变,横坐标变为原来的2倍,因此图形做了横向拉伸变化;
由(2)→(3):点A的横坐标没变,纵坐标变为原来的相反数,因此图形关于x轴对称;
由(3)→(4):图形中三个顶点的横坐标没变,纵坐标都增加了﹣1,即点A、点O、点B向下平移一个单位.因此图形做了平移变化.
PAGE
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
