人教版数学六年级下册3.1.2《圆柱的表面积》教案(表格版)
文档属性
| 名称 | 人教版数学六年级下册3.1.2《圆柱的表面积》教案(表格版) |
|
|
| 格式 | zip | ||
| 文件大小 | 54.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-02 00:00:00 | ||
图片预览

文档简介
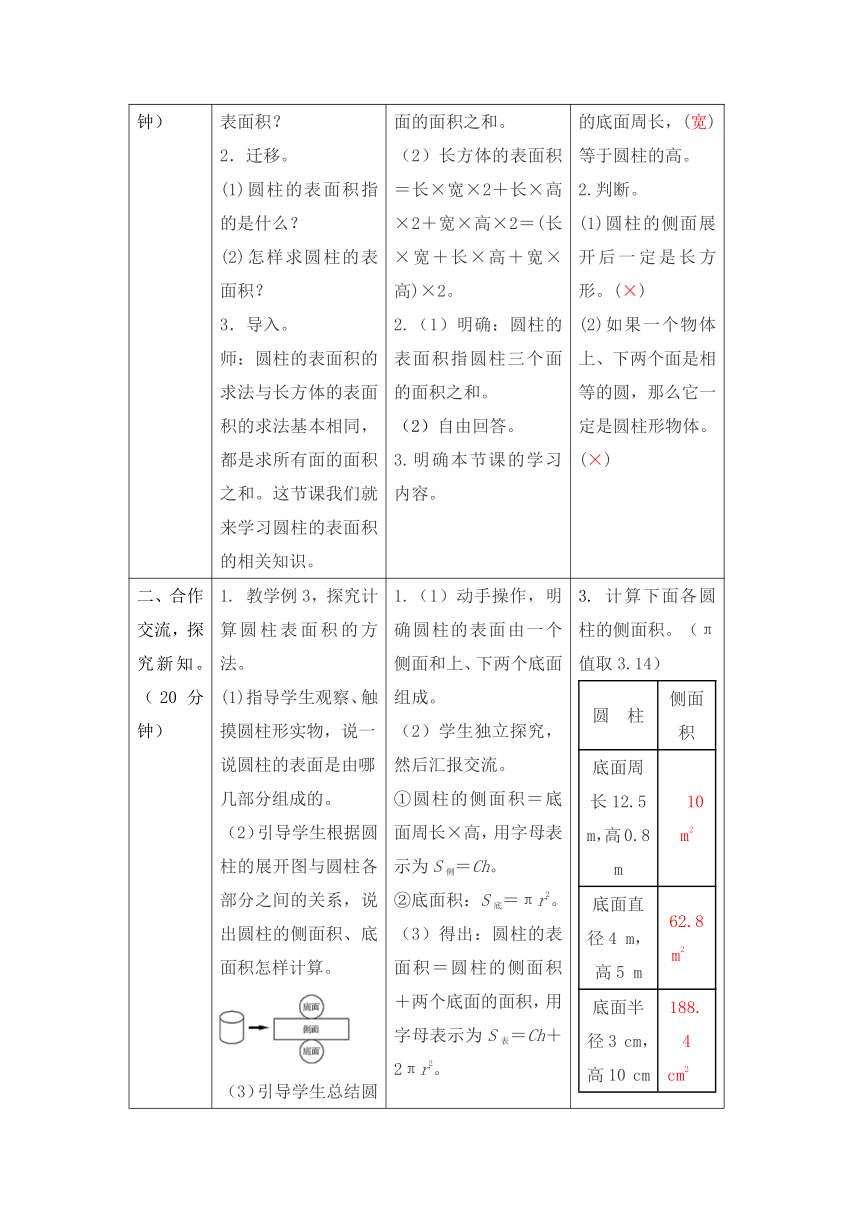
圆柱的表面积
教学设计表
学科:数学年级:六年级 册次:下学校: 教师:
课题
圆柱的表面积(P21例3、P22例4)
课型
新授课
计划学时
1
教学内容分析
例3教学圆柱表面积的概念,探究圆柱表面积的计算方法。例4是圆柱的表面积计算的实际应用。
承前启后
长方形、正方形、圆的面积计算、圆柱的组成→圆柱的表面积→组合图形的表面积
教学目标
1.理解圆柱的表面积的意义。
2.掌握圆柱的侧面积、表面积的计算方法,并能运用公式解决相关的问题。
3.经历圆柱的侧面积、表面积计算公式的推导过程,体验利用旧知迁移新知的学习方法。
重难点
重点:掌握圆柱侧面积、表面积的计算方法。
难点:灵活运用圆柱的侧面积、表面积的知识解决实际问题。
化解措施
知识迁移,动手操作
教学设计思路
复习铺垫,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
学生准备:圆柱形实物、纸制圆柱形厨师帽
教学过程
教师活动
学生活动
同步检测
一、复习铺垫,导入新课。(5分钟)
1.铺垫。
(1)长方体的表面积指的是什么?
(2)怎样求长方体的表面积?
2.迁移。
(1)圆柱的表面积指的是什么?
(2)怎样求圆柱的表面积?
3.导入。
师:圆柱的表面积的求法与长方体的表面积的求法基本相同,都是求所有面的面积之和。这节课我们就来学习圆柱的表面积的相关知识。
1. 思考后回答教师提出的问题。
(1)长方体的表面积指的是长方体的6个面的面积之和。
(2)长方体的表面积=长×宽×2+长×高×2+宽×高×2=(长×宽+长×高+宽×高)×2。
2.(1)明确:圆柱的表面积指圆柱三个面的面积之和。
(2)自由回答。
3.明确本节课的学习内容。
1.把一个圆柱的侧面沿高展开,得到一个长方形,它的(长)等于圆柱的底面周长,(宽)等于圆柱的高。
2.判断。
(1)圆柱的侧面展开后一定是长方形。(×)
(2)如果一个物体上、下两个面是相等的圆,那么它一定是圆柱形物体。(×)
二、合作交流,探究新知。(20分钟)
1. 教学例3,探究计算圆柱表面积的方法。
(1)指导学生观察、触摸圆柱形实物,说一说圆柱的表面是由哪几部分组成的。
(2)引导学生根据圆柱的展开图与圆柱各部分之间的关系,说出圆柱的侧面积、底面积怎样计算。
/
(3)引导学生总结圆柱表面积的计算公式。
2.教学例4,应用圆柱表面积的知识解决实际问题。
(1)课件出示例4,引导学生通过小组合作,明确解题思路。
(2)组织学生讨论解题时要注意的问题。
(3)引导学生进行计算,并汇报计算过程。
3.小结。
师:圆柱的表面积等于圆柱的侧面积加上两个底面的面积,但在运用这一公式解决实际问题时,究竟算几个面,要结合实际,灵活运用。
1.(1)动手操作,明确圆柱的表面由一个侧面和上、下两个底面组成。
(2)学生独立探究,然后汇报交流。
①圆柱的侧面积=底面周长×高,用字母表示为S侧=Ch。
②底面积:S底=πr2。
(3)得出:圆柱的表面积=圆柱的侧面积+两个底面的面积,用字母表示为S表=Ch+2πr2。
2.(1)通过小组讨论、交流,得出:求至少需要用多少面料,就是求圆柱形厨师帽的表面积,也就是求圆柱的表面积。
(2)小组讨论、交流后汇报。
①厨师帽没有下底面,计算表面积时只需要加一个底面的面积。
②计算结果要用“进一法”取近似值,因为实际使用的面料要比计算的结果多一些。
(3)独立计算后汇报计算过程。
帽子的侧面积:
3.14×20×30=1884(cm2)
帽顶的面积:
3.14×(20÷2)2=314(cm2)
需要用的面料:
1884+314=2198≈2200(cm2)
3.认真倾听教师的小结。
3. 计算下面各圆柱的侧面积。(π值取3.14)
圆 柱
侧面积
底面周长12.5 m,高0.8 m
?10 m2
底面直径4 m,高5 m
62.8 m2?
底面半径3 cm,高10 cm
188.4 cm2?
4.计算下面圆柱的表面积。(π值取3.14)
/
3.14×(
2
2
)2×2+3.14×2×1.5=15.7(cm2)
5. 时代广场有一个圆柱形喷水池,底面直径是5 m,深0.8 m,如果要在喷水池的底面和内壁贴上瓷砖,贴瓷砖的面积是多少平方米?(π值取3.14)
3.14×(
5
2
)2+3.14×5×0.8=32.185(m2)
三、巩固应用,提升能力。(10分钟)
1.完成教材第21页“做一做”。
2.完成教材第22页“做一做”。
3.完成教材第23页第2题。
1.独立完成并汇报结果。
2.小组讨论,集体完成。
3.理解求压路的面积就是求圆柱的侧面积。
6. 一个圆柱形笔筒,底面半径是4 cm,高是10 cm,它的表面积是(301.44)cm2。(π值取3.14)
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.已知圆柱的底面半径和高,可以根据公式S表=2πrh+2πr2直接求出圆柱的表面积。
3. 已知圆柱的底面直径和高,求圆柱的表面积时,可以根据公式S表=πdh+来求。
4. 已知圆柱的底面周长和高,求圆柱的表面积,可以根据公式S表=Ch+π(C÷π÷2)2×2?来求。
教师个人补充意见:
板书设计
圆柱的表面积
/ / /
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的表面积=圆柱的侧面积+底面积×2
S表=Ch+2πr2
培优作业
一个长方形的塑料板,利用图中的阴影部分刚好能做成一个圆柱形的带盖水桶(接头处忽略不计)。求这个水桶的表面积。(π值取3.14)
/
水桶的底面直径:16.56÷(1+3.14)=4(dm)
水桶的高:4×2=8(dm)
水桶的表面积:3.14×(
4
2
)2×2+3.14×4×8=125.6(dm2)
教学反思
直观演示可以使学生获得丰富的感性材料,加深对知识本质的理解,有利于培养学生的形象思维能力。因此,在教学中不但要鼓励学生大胆猜想,还要借助多媒体教学,帮助学生建立起圆柱各部分之间的联系,使学生轻松得出结论。
微课设计点
教师可围绕“圆柱表面积的计算方法”设计微课。
教学设计表
学科:数学年级:六年级 册次:下学校: 教师:
课题
圆柱的表面积(P21例3、P22例4)
课型
新授课
计划学时
1
教学内容分析
例3教学圆柱表面积的概念,探究圆柱表面积的计算方法。例4是圆柱的表面积计算的实际应用。
承前启后
长方形、正方形、圆的面积计算、圆柱的组成→圆柱的表面积→组合图形的表面积
教学目标
1.理解圆柱的表面积的意义。
2.掌握圆柱的侧面积、表面积的计算方法,并能运用公式解决相关的问题。
3.经历圆柱的侧面积、表面积计算公式的推导过程,体验利用旧知迁移新知的学习方法。
重难点
重点:掌握圆柱侧面积、表面积的计算方法。
难点:灵活运用圆柱的侧面积、表面积的知识解决实际问题。
化解措施
知识迁移,动手操作
教学设计思路
复习铺垫,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
学生准备:圆柱形实物、纸制圆柱形厨师帽
教学过程
教师活动
学生活动
同步检测
一、复习铺垫,导入新课。(5分钟)
1.铺垫。
(1)长方体的表面积指的是什么?
(2)怎样求长方体的表面积?
2.迁移。
(1)圆柱的表面积指的是什么?
(2)怎样求圆柱的表面积?
3.导入。
师:圆柱的表面积的求法与长方体的表面积的求法基本相同,都是求所有面的面积之和。这节课我们就来学习圆柱的表面积的相关知识。
1. 思考后回答教师提出的问题。
(1)长方体的表面积指的是长方体的6个面的面积之和。
(2)长方体的表面积=长×宽×2+长×高×2+宽×高×2=(长×宽+长×高+宽×高)×2。
2.(1)明确:圆柱的表面积指圆柱三个面的面积之和。
(2)自由回答。
3.明确本节课的学习内容。
1.把一个圆柱的侧面沿高展开,得到一个长方形,它的(长)等于圆柱的底面周长,(宽)等于圆柱的高。
2.判断。
(1)圆柱的侧面展开后一定是长方形。(×)
(2)如果一个物体上、下两个面是相等的圆,那么它一定是圆柱形物体。(×)
二、合作交流,探究新知。(20分钟)
1. 教学例3,探究计算圆柱表面积的方法。
(1)指导学生观察、触摸圆柱形实物,说一说圆柱的表面是由哪几部分组成的。
(2)引导学生根据圆柱的展开图与圆柱各部分之间的关系,说出圆柱的侧面积、底面积怎样计算。
/
(3)引导学生总结圆柱表面积的计算公式。
2.教学例4,应用圆柱表面积的知识解决实际问题。
(1)课件出示例4,引导学生通过小组合作,明确解题思路。
(2)组织学生讨论解题时要注意的问题。
(3)引导学生进行计算,并汇报计算过程。
3.小结。
师:圆柱的表面积等于圆柱的侧面积加上两个底面的面积,但在运用这一公式解决实际问题时,究竟算几个面,要结合实际,灵活运用。
1.(1)动手操作,明确圆柱的表面由一个侧面和上、下两个底面组成。
(2)学生独立探究,然后汇报交流。
①圆柱的侧面积=底面周长×高,用字母表示为S侧=Ch。
②底面积:S底=πr2。
(3)得出:圆柱的表面积=圆柱的侧面积+两个底面的面积,用字母表示为S表=Ch+2πr2。
2.(1)通过小组讨论、交流,得出:求至少需要用多少面料,就是求圆柱形厨师帽的表面积,也就是求圆柱的表面积。
(2)小组讨论、交流后汇报。
①厨师帽没有下底面,计算表面积时只需要加一个底面的面积。
②计算结果要用“进一法”取近似值,因为实际使用的面料要比计算的结果多一些。
(3)独立计算后汇报计算过程。
帽子的侧面积:
3.14×20×30=1884(cm2)
帽顶的面积:
3.14×(20÷2)2=314(cm2)
需要用的面料:
1884+314=2198≈2200(cm2)
3.认真倾听教师的小结。
3. 计算下面各圆柱的侧面积。(π值取3.14)
圆 柱
侧面积
底面周长12.5 m,高0.8 m
?10 m2
底面直径4 m,高5 m
62.8 m2?
底面半径3 cm,高10 cm
188.4 cm2?
4.计算下面圆柱的表面积。(π值取3.14)
/
3.14×(
2
2
)2×2+3.14×2×1.5=15.7(cm2)
5. 时代广场有一个圆柱形喷水池,底面直径是5 m,深0.8 m,如果要在喷水池的底面和内壁贴上瓷砖,贴瓷砖的面积是多少平方米?(π值取3.14)
3.14×(
5
2
)2+3.14×5×0.8=32.185(m2)
三、巩固应用,提升能力。(10分钟)
1.完成教材第21页“做一做”。
2.完成教材第22页“做一做”。
3.完成教材第23页第2题。
1.独立完成并汇报结果。
2.小组讨论,集体完成。
3.理解求压路的面积就是求圆柱的侧面积。
6. 一个圆柱形笔筒,底面半径是4 cm,高是10 cm,它的表面积是(301.44)cm2。(π值取3.14)
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.已知圆柱的底面半径和高,可以根据公式S表=2πrh+2πr2直接求出圆柱的表面积。
3. 已知圆柱的底面直径和高,求圆柱的表面积时,可以根据公式S表=πdh+来求。
4. 已知圆柱的底面周长和高,求圆柱的表面积,可以根据公式S表=Ch+π(C÷π÷2)2×2?来求。
教师个人补充意见:
板书设计
圆柱的表面积
/ / /
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的表面积=圆柱的侧面积+底面积×2
S表=Ch+2πr2
培优作业
一个长方形的塑料板,利用图中的阴影部分刚好能做成一个圆柱形的带盖水桶(接头处忽略不计)。求这个水桶的表面积。(π值取3.14)
/
水桶的底面直径:16.56÷(1+3.14)=4(dm)
水桶的高:4×2=8(dm)
水桶的表面积:3.14×(
4
2
)2×2+3.14×4×8=125.6(dm2)
教学反思
直观演示可以使学生获得丰富的感性材料,加深对知识本质的理解,有利于培养学生的形象思维能力。因此,在教学中不但要鼓励学生大胆猜想,还要借助多媒体教学,帮助学生建立起圆柱各部分之间的联系,使学生轻松得出结论。
微课设计点
教师可围绕“圆柱表面积的计算方法”设计微课。
