人教版数学六年级下册4.1.3《解比例》教案(表格版)
文档属性
| 名称 | 人教版数学六年级下册4.1.3《解比例》教案(表格版) | 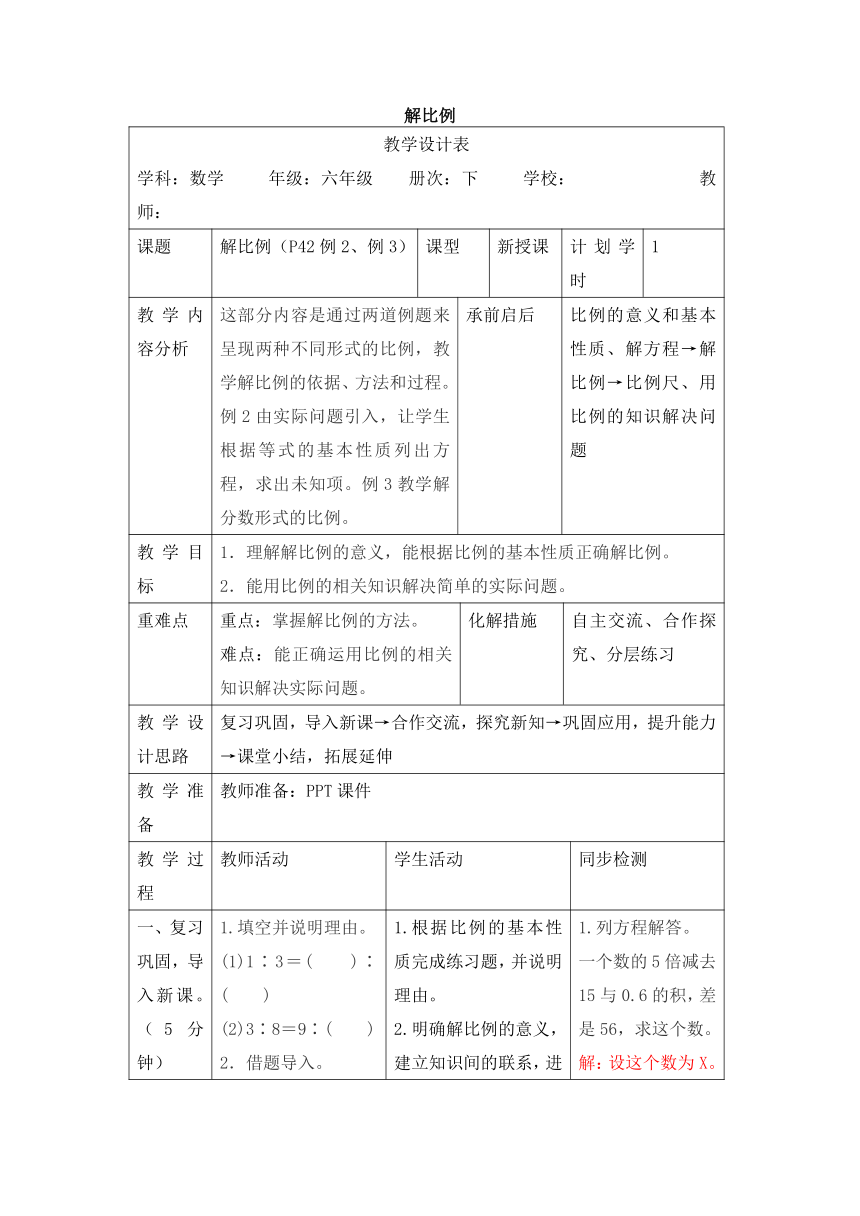 | |
| 格式 | zip | ||
| 文件大小 | 28.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-02 08:47:25 | ||
图片预览


文档简介
解比例
教学设计表
学科:数学 年级:六年级 册次:下 学校: 教师:
课题
解比例(P42例2、例3)
课型
新授课
计划学时
1
教学内容分析
这部分内容是通过两道例题来呈现两种不同形式的比例,教学解比例的依据、方法和过程。例2由实际问题引入,让学生根据等式的基本性质列出方程,求出未知项。例3教学解分数形式的比例。
承前启后
比例的意义和基本性质、解方程→解比例→比例尺、用比例的知识解决问题
教学目标
1.理解解比例的意义,能根据比例的基本性质正确解比例。
2.能用比例的相关知识解决简单的实际问题。
重难点
重点:掌握解比例的方法。
难点:能正确运用比例的相关知识解决实际问题。
化解措施
自主交流、合作探究、分层练习
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.填空并说明理由。
(1)1∶3=( )∶( )
(2)3∶8=9∶( )
2.借题导入。
师:3∶8=9∶( )中的未知项也可以用x表示,写作3∶8=9∶x,求比例中的未知项,叫作解比例。
根据比例的基本性质完成练习题,并说明理由。
明确解比例的意义,建立知识间的联系,进入新课的学习。
1.列方程解答。
一个数的5倍减去15与0.6的积,差是56,求这个数。
解:设这个数为X。
5x-15×0.6=56
X=13
2.在括号里填上适当的数。
3∶5=36∶(60)
(48)∶12=4∶1
二、合作交流,探究新知。(20分钟)
1.教学例2,探究解比例的方法。
(1)课件出示例2,组织学生自由读题,找出题中的已知条件和所求问题。
(2)引导学生理解“1∶10”的意义。
(3)指导学生根据题意写出比例,并引导学生明确未知项可设x代替。
(4)指导学生根据比例的基本性质,将比例转化成方程,再根据解方程的方法求出未知数x,注意提醒学生列比例前要先写设语。
(5)组织学生汇报、并交流列式及解答的依据。
2.教学例3,探究分数形式的比例的解法。
(1)课件出示例3,让学生尝试解比例。
(2)汇报解题思路和方法。
3.引导学生总结解比例的过程,并结合解比例的过程,思考:解比例首先要做什么?然后做什么?
探究解比例的方法。
读题,找出题中的已知条件和所求问题。
明确:模型的高度∶实际的高度=1∶10。
(3)小组讨论、交流,根据相关量之间的关系,尝试列出比例:x:320=1:10。
(4)根据比例的基本性质尝试完成解比例的全过程,并汇报:
解:设这座模型的高度是x?m。
x∶320=1∶10
10x=320×1
x=
x=32
答:这座模型高32 m。
(5)汇报、并交流列式及解答的依据。
2.(1)小组合作交流,尝试解比例。
(2)汇报解法:根据比例的基本性质,把等号两端的分子和分母分别交叉相乘,得到方程2.4x=1.5×6,然后方程的两边同时除以2.4,得出x=3.75。
3.通过讨论明确解比例的过程:根据比例的基本性质把比例转化成方程,再根据以前学的解方程的方法求解。
解比例。
x∶30=20∶12
x=50
x=3
4.南京长江大桥铁路桥模型长6.772 m,它的实际长度和模型长度的比约为1000∶1,南京长江大桥铁路桥的实际长度约为多少米?
解:设南京长江大桥铁路桥的实际长度约为x?m。
x∶6.772=1000∶1 x=6772
5.配制一种农药,药粉和水的质量比是1∶500,现在有水6000 kg,配制这种农药需要药粉多少千克?
解:设配制这种农药需要药粉x?kg。
x∶6000=1∶500
x=12
三、巩固应用,提升能力。(10分钟)
1.完成教材第42页“做一做”。
2.完成教材第44页第8题。
1.独立完成,指名板演。
2.独立完成并汇报结果。
6.一个长方形的长与宽的比是5:3,已知长是2厘米,宽是多少?
1.2厘米
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.根据比例的基本性质解比例时,应该先把比例转化成“两个外项的积=两个内项的积”的形式,再解方程。
3.解分数形式的比例时,应遵循“十字相乘”的原则。
教师个人补充意见:
板书设计
培优作业
用2,3.6,4.5和x组成比例,并求出x的值。
(1)x和2同时为内项(或外项)。
3.6∶x=2∶4.5
2x=3.6×4.5
x=8.1
(2)x和3.6同时为内项(或外项)。
2∶x=3.6∶4.5
3.6x=2×4.5
x=2.5
(3)x和4.5同时为内项(或外项)。
2∶x=4.5∶3.6
4.5x=2×3.6
x=1.6
教学反思
在教学中,采取用原有知识推动新知识的学习策略,巧妙地引导学生将解比例转化成解方程,推动学生走向自主探索之路,使学生主动参与学习的全过程,在把新知融入到原有知识结构的过程中,获得成功的体验。
微课设计点
教师可围绕“解比例的依据和方法”设计微课。
教学设计表
学科:数学 年级:六年级 册次:下 学校: 教师:
课题
解比例(P42例2、例3)
课型
新授课
计划学时
1
教学内容分析
这部分内容是通过两道例题来呈现两种不同形式的比例,教学解比例的依据、方法和过程。例2由实际问题引入,让学生根据等式的基本性质列出方程,求出未知项。例3教学解分数形式的比例。
承前启后
比例的意义和基本性质、解方程→解比例→比例尺、用比例的知识解决问题
教学目标
1.理解解比例的意义,能根据比例的基本性质正确解比例。
2.能用比例的相关知识解决简单的实际问题。
重难点
重点:掌握解比例的方法。
难点:能正确运用比例的相关知识解决实际问题。
化解措施
自主交流、合作探究、分层练习
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.填空并说明理由。
(1)1∶3=( )∶( )
(2)3∶8=9∶( )
2.借题导入。
师:3∶8=9∶( )中的未知项也可以用x表示,写作3∶8=9∶x,求比例中的未知项,叫作解比例。
根据比例的基本性质完成练习题,并说明理由。
明确解比例的意义,建立知识间的联系,进入新课的学习。
1.列方程解答。
一个数的5倍减去15与0.6的积,差是56,求这个数。
解:设这个数为X。
5x-15×0.6=56
X=13
2.在括号里填上适当的数。
3∶5=36∶(60)
(48)∶12=4∶1
二、合作交流,探究新知。(20分钟)
1.教学例2,探究解比例的方法。
(1)课件出示例2,组织学生自由读题,找出题中的已知条件和所求问题。
(2)引导学生理解“1∶10”的意义。
(3)指导学生根据题意写出比例,并引导学生明确未知项可设x代替。
(4)指导学生根据比例的基本性质,将比例转化成方程,再根据解方程的方法求出未知数x,注意提醒学生列比例前要先写设语。
(5)组织学生汇报、并交流列式及解答的依据。
2.教学例3,探究分数形式的比例的解法。
(1)课件出示例3,让学生尝试解比例。
(2)汇报解题思路和方法。
3.引导学生总结解比例的过程,并结合解比例的过程,思考:解比例首先要做什么?然后做什么?
探究解比例的方法。
读题,找出题中的已知条件和所求问题。
明确:模型的高度∶实际的高度=1∶10。
(3)小组讨论、交流,根据相关量之间的关系,尝试列出比例:x:320=1:10。
(4)根据比例的基本性质尝试完成解比例的全过程,并汇报:
解:设这座模型的高度是x?m。
x∶320=1∶10
10x=320×1
x=
x=32
答:这座模型高32 m。
(5)汇报、并交流列式及解答的依据。
2.(1)小组合作交流,尝试解比例。
(2)汇报解法:根据比例的基本性质,把等号两端的分子和分母分别交叉相乘,得到方程2.4x=1.5×6,然后方程的两边同时除以2.4,得出x=3.75。
3.通过讨论明确解比例的过程:根据比例的基本性质把比例转化成方程,再根据以前学的解方程的方法求解。
解比例。
x∶30=20∶12
x=50
x=3
4.南京长江大桥铁路桥模型长6.772 m,它的实际长度和模型长度的比约为1000∶1,南京长江大桥铁路桥的实际长度约为多少米?
解:设南京长江大桥铁路桥的实际长度约为x?m。
x∶6.772=1000∶1 x=6772
5.配制一种农药,药粉和水的质量比是1∶500,现在有水6000 kg,配制这种农药需要药粉多少千克?
解:设配制这种农药需要药粉x?kg。
x∶6000=1∶500
x=12
三、巩固应用,提升能力。(10分钟)
1.完成教材第42页“做一做”。
2.完成教材第44页第8题。
1.独立完成,指名板演。
2.独立完成并汇报结果。
6.一个长方形的长与宽的比是5:3,已知长是2厘米,宽是多少?
1.2厘米
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.根据比例的基本性质解比例时,应该先把比例转化成“两个外项的积=两个内项的积”的形式,再解方程。
3.解分数形式的比例时,应遵循“十字相乘”的原则。
教师个人补充意见:
板书设计
培优作业
用2,3.6,4.5和x组成比例,并求出x的值。
(1)x和2同时为内项(或外项)。
3.6∶x=2∶4.5
2x=3.6×4.5
x=8.1
(2)x和3.6同时为内项(或外项)。
2∶x=3.6∶4.5
3.6x=2×4.5
x=2.5
(3)x和4.5同时为内项(或外项)。
2∶x=4.5∶3.6
4.5x=2×3.6
x=1.6
教学反思
在教学中,采取用原有知识推动新知识的学习策略,巧妙地引导学生将解比例转化成解方程,推动学生走向自主探索之路,使学生主动参与学习的全过程,在把新知融入到原有知识结构的过程中,获得成功的体验。
微课设计点
教师可围绕“解比例的依据和方法”设计微课。
