人教版数学六年级下册4.3.4《用比例解决问题》教案(表格版)
文档属性
| 名称 | 人教版数学六年级下册4.3.4《用比例解决问题》教案(表格版) | 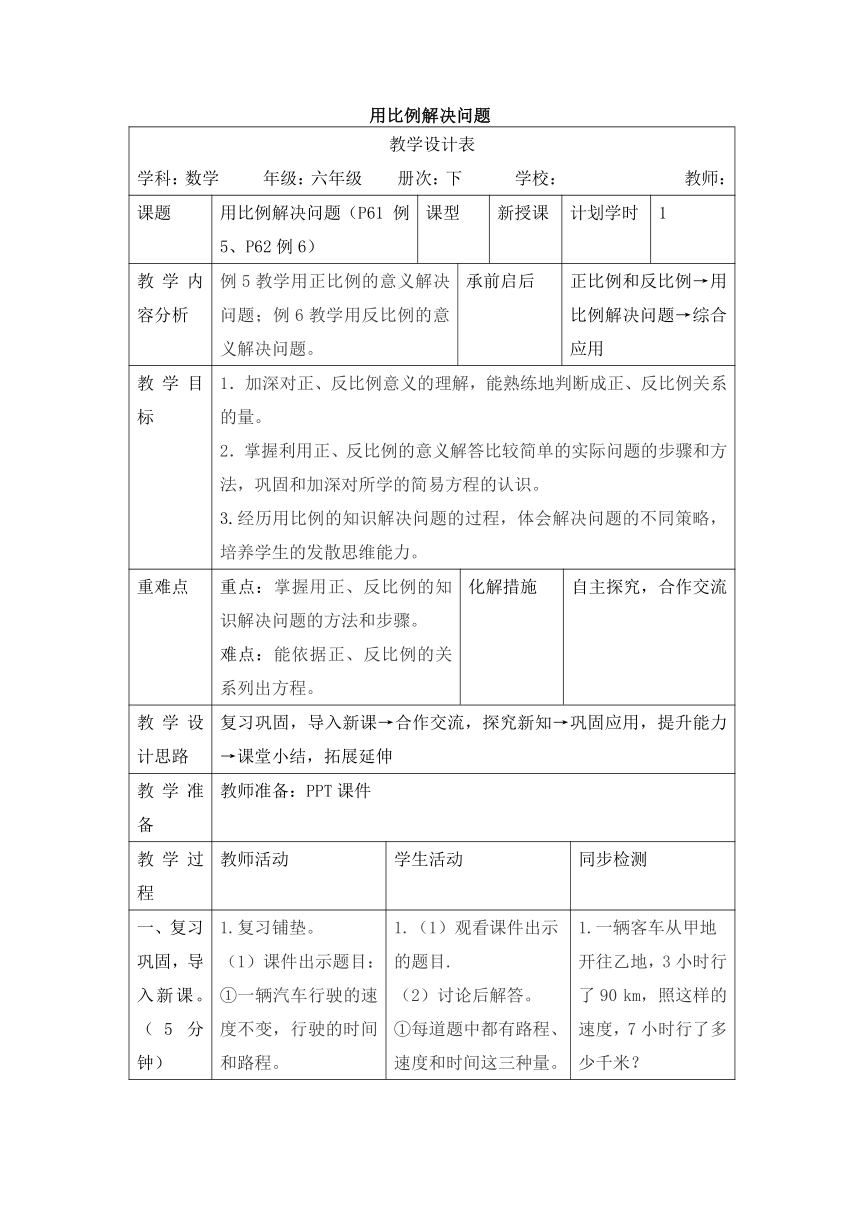 | |
| 格式 | zip | ||
| 文件大小 | 29.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-02 09:05:08 | ||
图片预览


文档简介
用比例解决问题
教学设计表
学科:数学 年级:六年级 册次:下 学校: 教师:
课题
用比例解决问题(P61 例5、P62例6)
课型
新授课
计划学时
1
教学内容分析
例5教学用正比例的意义解决问题;例6教学用反比例的意义解决问题。
承前启后
正比例和反比例→用比例解决问题→综合应用
教学目标
1.加深对正、反比例意义的理解,能熟练地判断成正、反比例关系的量。
2.掌握利用正、反比例的意义解答比较简单的实际问题的步骤和方法,巩固和加深对所学的简易方程的认识。
3.经历用比例的知识解决问题的过程,体会解决问题的不同策略,培养学生的发散思维能力。
重难点
重点:掌握用正、反比例的知识解决问题的方法和步骤。
难点:能依据正、反比例的关系列出方程。
化解措施
自主探究,合作交流
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.复习铺垫。
(1)课件出示题目:
①一辆汽车行驶的速度不变,行驶的时间和路程。
②一辆汽车从甲地开往乙地,行驶的速度和时间。
(2)提出问题:
①每道题中各有哪三种量?
②其中哪种量是不变的?
③相关联的量成什么比例关系?
2.引入新课。
师:生产、生活中的一些实际问题也可以应用比例的知识来解决。今天,我们就来学习用正、反比例的知识解决问题。
1.(1)观看课件出示的题目.
(2)讨论后解答。
①每道题中都有路程、速度和时间这三种量。
②第一道题中速度是不变的;第二道题中路程是不变的。
③第一道题中路程和时间成正比例关系;第二道题中速度和时间成反比例关系。
2.明确本节课的学习内容。
1.一辆客车从甲地开往乙地,3小时行了90 km,照这样的速度,7小时行了多少千米?
90÷3=30(km/h)
30×7=210(km)
二、合作交流,探究新知。(20分钟)
1.用算术法解决问题。
(1)课件出示教材第61页例5,让学生找出题中的已知条件与所求问题。
(2)组织学生独立解答,交流解答的方法。
2.引导用正比例的知识解决问题:
(1)思考和讨论以下问题。
①题中两种相关联的量成什么比例?
②两家的水费与用水的吨数的比值有什么关系?
(2)指导学生根据比例的意义列出方程并解答。
(3)拓展练习:王大爷家上个月的水费是42元,上个月用了多少吨水?
3.用反比例的知识解决问题。
(1)课件出示教材第62页例6,指导学生分析题意,独立解答并汇报。
(2)拓展练习:现在30天的用电量原来只够用多少天?
4.总结用正、反比例的知识解题的思路。
(1)引导学生结合例5、例6的解题过程,总结用比例的知识解决问题的步骤。
(2)组织学生说一说:用比例的知识解题的关键是什么?怎样列出等式?
1.(1)认真观察课件,找出题中的已知条件和所求问题。
(2)独立解答并汇报。
明确:可以用算术法解决。先求出每吨水的价钱,再求出10 吨水的价钱,列式为28÷8×10。
2.(1)讨论后汇报:因为每吨水的价钱一定,所以水费和用水的吨数成正比例,也就是说,两家的水费和用水吨数的比值相等。
(2)根据比例的意义列方程解答后,全班交流解题过程。
(3)分析题意,独立解答后,交流解题思路和解题方法。
3.(1)独立解答并汇报。
(2)独立解答后,交流解题思路和解题方法。
4.交流、总结。
(1)讨论并汇报解题步骤:
①分析题意,判断两种相关联的量成什么比例关系;
②找出两种相关联的量的对应数值,根据比值一定或乘积一定列出比例;
③解比例,检验并写出答语。
(2)明确:解题的关键是正确判断两种相关联的量成什么比例。成正比例根据比值相等列式解答,成反比例根据乘积相等列式解答。
2.一辆货车去距出发地360 km的灾区送救灾物资,1.5小时行驶了90 km,照这样的速度,几小时能到达灾区?
(1)题中相关联的两种量是(路程)和(时间)。
(2)根据“照这样的速度”这句话,可知这辆货车行驶的(速度)是一定的,(路程)和(时间)成正比例关系。
(3)列出比例是(/)(用x表示时间)。
3.用3辆同样的汽车一次可运面粉480袋,照这样计算,用7辆同样的汽车一次可运面粉多少袋?如果设用7辆同样的汽车一次可运面粉x袋,那么可列式为(x∶7=480∶3)。
/
三、巩固应用,提升能力。(10分钟)
1.完成教材第62页“做一做”第1,2题。
2.完成教材第64页第7题。
1.先判断每题中的两种量成什么比例关系,再进行解答。
2.独立完成,汇报时说明理由。
5.一种农药,药液与水的质量之比是1∶1000。用30 g药液配制这种农药需要加水多少克?
30000g
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.用比例的知识解决问题的关键是根据不变量来判断两种相关联的量成哪种比例关系。
教师个人补充意见:
板书设计
/
培优作业
甲、乙两个圆柱形容器底面积之比为4∶3,甲容器中水深7 cm,乙容器中水深3 cm,往两个容器中注入同样多的水,直到水深相等,这时甲容器的水面上升多少厘米?
解:设甲容器的水面上升x?cm。
4x=(7-3+x)×3
4x=4×3+3x
x=12
答:甲容器的水面上升12 cm。
教学反思
温故而知新,本节课重在引导学生系统地整理和复习正、反比例的相关知识,让学生经历数学知识的应用过程。在探索过程中,鼓励学生创造性地运用所学知识解决问题,使学生进一步掌握并巩固用比例的知识解决应用题的方法,同时提高学生的自学能力,激发学生的学习兴趣。
微课设计点
教师可围绕“用比例解决问题的步骤”设计微课。
教学设计表
学科:数学 年级:六年级 册次:下 学校: 教师:
课题
用比例解决问题(P61 例5、P62例6)
课型
新授课
计划学时
1
教学内容分析
例5教学用正比例的意义解决问题;例6教学用反比例的意义解决问题。
承前启后
正比例和反比例→用比例解决问题→综合应用
教学目标
1.加深对正、反比例意义的理解,能熟练地判断成正、反比例关系的量。
2.掌握利用正、反比例的意义解答比较简单的实际问题的步骤和方法,巩固和加深对所学的简易方程的认识。
3.经历用比例的知识解决问题的过程,体会解决问题的不同策略,培养学生的发散思维能力。
重难点
重点:掌握用正、反比例的知识解决问题的方法和步骤。
难点:能依据正、反比例的关系列出方程。
化解措施
自主探究,合作交流
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教师准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.复习铺垫。
(1)课件出示题目:
①一辆汽车行驶的速度不变,行驶的时间和路程。
②一辆汽车从甲地开往乙地,行驶的速度和时间。
(2)提出问题:
①每道题中各有哪三种量?
②其中哪种量是不变的?
③相关联的量成什么比例关系?
2.引入新课。
师:生产、生活中的一些实际问题也可以应用比例的知识来解决。今天,我们就来学习用正、反比例的知识解决问题。
1.(1)观看课件出示的题目.
(2)讨论后解答。
①每道题中都有路程、速度和时间这三种量。
②第一道题中速度是不变的;第二道题中路程是不变的。
③第一道题中路程和时间成正比例关系;第二道题中速度和时间成反比例关系。
2.明确本节课的学习内容。
1.一辆客车从甲地开往乙地,3小时行了90 km,照这样的速度,7小时行了多少千米?
90÷3=30(km/h)
30×7=210(km)
二、合作交流,探究新知。(20分钟)
1.用算术法解决问题。
(1)课件出示教材第61页例5,让学生找出题中的已知条件与所求问题。
(2)组织学生独立解答,交流解答的方法。
2.引导用正比例的知识解决问题:
(1)思考和讨论以下问题。
①题中两种相关联的量成什么比例?
②两家的水费与用水的吨数的比值有什么关系?
(2)指导学生根据比例的意义列出方程并解答。
(3)拓展练习:王大爷家上个月的水费是42元,上个月用了多少吨水?
3.用反比例的知识解决问题。
(1)课件出示教材第62页例6,指导学生分析题意,独立解答并汇报。
(2)拓展练习:现在30天的用电量原来只够用多少天?
4.总结用正、反比例的知识解题的思路。
(1)引导学生结合例5、例6的解题过程,总结用比例的知识解决问题的步骤。
(2)组织学生说一说:用比例的知识解题的关键是什么?怎样列出等式?
1.(1)认真观察课件,找出题中的已知条件和所求问题。
(2)独立解答并汇报。
明确:可以用算术法解决。先求出每吨水的价钱,再求出10 吨水的价钱,列式为28÷8×10。
2.(1)讨论后汇报:因为每吨水的价钱一定,所以水费和用水的吨数成正比例,也就是说,两家的水费和用水吨数的比值相等。
(2)根据比例的意义列方程解答后,全班交流解题过程。
(3)分析题意,独立解答后,交流解题思路和解题方法。
3.(1)独立解答并汇报。
(2)独立解答后,交流解题思路和解题方法。
4.交流、总结。
(1)讨论并汇报解题步骤:
①分析题意,判断两种相关联的量成什么比例关系;
②找出两种相关联的量的对应数值,根据比值一定或乘积一定列出比例;
③解比例,检验并写出答语。
(2)明确:解题的关键是正确判断两种相关联的量成什么比例。成正比例根据比值相等列式解答,成反比例根据乘积相等列式解答。
2.一辆货车去距出发地360 km的灾区送救灾物资,1.5小时行驶了90 km,照这样的速度,几小时能到达灾区?
(1)题中相关联的两种量是(路程)和(时间)。
(2)根据“照这样的速度”这句话,可知这辆货车行驶的(速度)是一定的,(路程)和(时间)成正比例关系。
(3)列出比例是(/)(用x表示时间)。
3.用3辆同样的汽车一次可运面粉480袋,照这样计算,用7辆同样的汽车一次可运面粉多少袋?如果设用7辆同样的汽车一次可运面粉x袋,那么可列式为(x∶7=480∶3)。
/
三、巩固应用,提升能力。(10分钟)
1.完成教材第62页“做一做”第1,2题。
2.完成教材第64页第7题。
1.先判断每题中的两种量成什么比例关系,再进行解答。
2.独立完成,汇报时说明理由。
5.一种农药,药液与水的质量之比是1∶1000。用30 g药液配制这种农药需要加水多少克?
30000g
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.用比例的知识解决问题的关键是根据不变量来判断两种相关联的量成哪种比例关系。
教师个人补充意见:
板书设计
/
培优作业
甲、乙两个圆柱形容器底面积之比为4∶3,甲容器中水深7 cm,乙容器中水深3 cm,往两个容器中注入同样多的水,直到水深相等,这时甲容器的水面上升多少厘米?
解:设甲容器的水面上升x?cm。
4x=(7-3+x)×3
4x=4×3+3x
x=12
答:甲容器的水面上升12 cm。
教学反思
温故而知新,本节课重在引导学生系统地整理和复习正、反比例的相关知识,让学生经历数学知识的应用过程。在探索过程中,鼓励学生创造性地运用所学知识解决问题,使学生进一步掌握并巩固用比例的知识解决应用题的方法,同时提高学生的自学能力,激发学生的学习兴趣。
微课设计点
教师可围绕“用比例解决问题的步骤”设计微课。
