人教版数学六年级下册5.1《鸽巢原理》教案(表格版)
文档属性
| 名称 | 人教版数学六年级下册5.1《鸽巢原理》教案(表格版) | 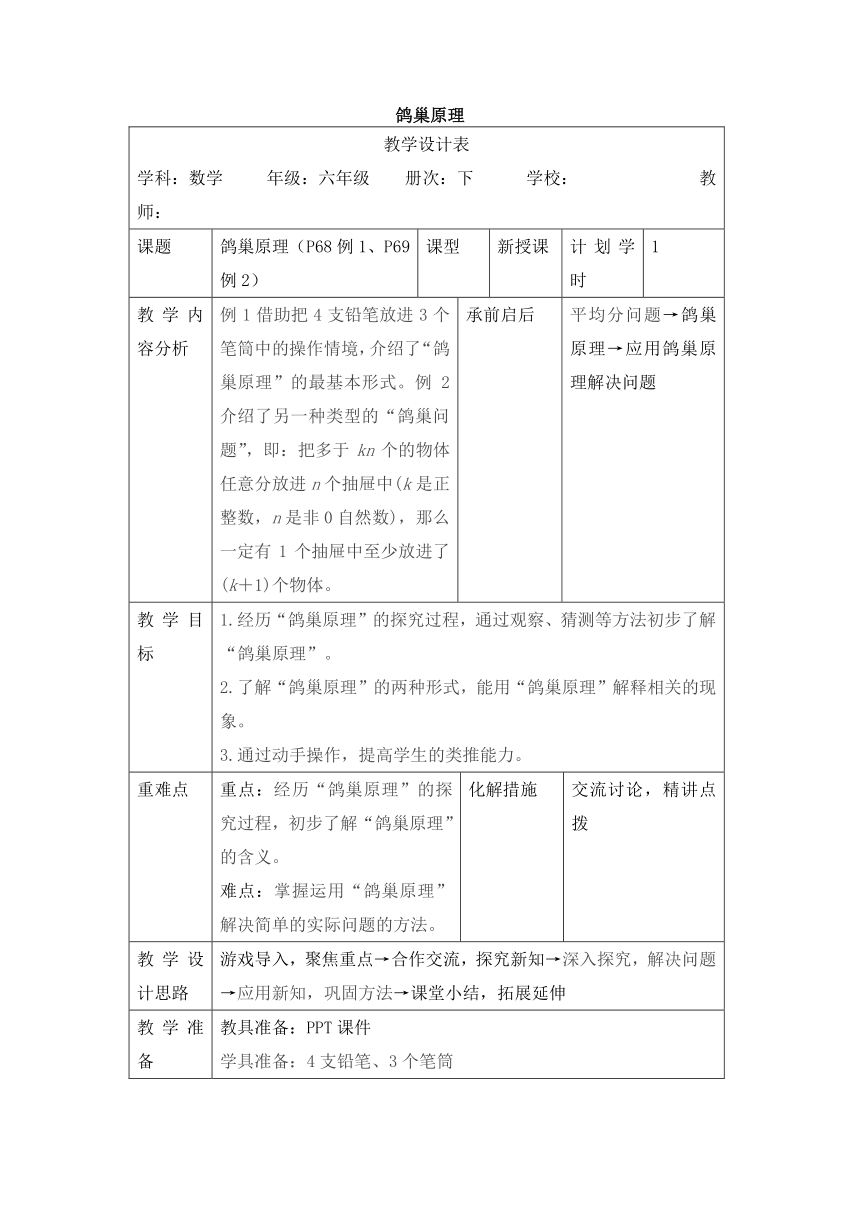 | |
| 格式 | zip | ||
| 文件大小 | 21.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-02 09:07:12 | ||
图片预览



文档简介
鸽巢原理
教学设计表
学科:数学 年级:六年级 册次:下 学校: 教师:
课题
鸽巢原理(P68例1、P69例2)
课型
新授课
计划学时
1
教学内容分析
例1借助把4支铅笔放进3个笔筒中的操作情境,介绍了“鸽巢原理”的最基本形式。例2介绍了另一种类型的“鸽巢问题”,即:把多于kn个的物体任意分放进n个抽屉中(k是正整数,n是非0自然数),那么一定有1个抽屉中至少放进了(k+1)个物体。
承前启后
平均分问题→鸽巢原理→应用鸽巢原理解决问题
教学目标
1.经历“鸽巢原理”的探究过程,通过观察、猜测等方法初步了解“鸽巢原理”。
2.了解“鸽巢原理”的两种形式,能用“鸽巢原理”解释相关的现象。
3.通过动手操作,提高学生的类推能力。
重难点
重点:经历“鸽巢原理”的探究过程,初步了解“鸽巢原理”的含义。
难点:掌握运用“鸽巢原理”解决简单的实际问题的方法。
化解措施
交流讨论,精讲点拨
教学设计思路
游戏导入,聚焦重点→合作交流,探究新知→深入探究,解决问题→应用新知,巩固方法→课堂小结,拓展延伸
教学准备
教具准备:PPT课件
学具准备:4支铅笔、3个笔筒
教学过程
教师活动
学生活动
同步检测
一、游戏导入,聚焦重点。(5分钟)
1.组织学生玩“抽扑克牌”游戏。
(1)准备一副扑克牌,取出大王、小王。选出5位同学,请他们任意抽取1张扑克牌并记在心里,把牌收好。
(2)教师猜测:在这5张扑克牌里,至少有2张是同一花色的。
(3)验证猜想。
(4)再次游戏。
请一名同学抽出14张牌,发现:这14张牌中至少有一对儿。
(5)课件出示:5张牌中至少有2张是同一花色的;14张牌中至少有一对儿。组织学生说一说“至少”的含义。
2.引入新课。
师:老师为什么能作出准确的判断呢?因为这个游戏中蕴含着一个数学原理,这节课我们就一起来研究这个原理。
1.游戏互动,猜想验证。
(1)明确游戏规则,各组选代表参与“抽扑克牌”游戏。
(2)与教师一起猜测结果。
(3)学生代表打开手里的扑克牌,验证教师的猜想,初步感知“至少”的含义。
(4)再次游戏,进一步理解“至少”的含义。
(5)观看课件出示的两句话,用自己的语言说一说“至少”的含义。
(“至少”是指最小的限度,最少。)
2.明确本节课的学习内容。
1.100名同学平均分成5组,每组有多少人?
100÷5=20(人)
2.30名同学去旅游,如果每4人住1间房,那么一共需要几间房?
30÷4=7(间)……2(人)
7+1=8(间)
二、合作交流,探究新知。(13分钟)
1.教学例1,探究鸽巢原理(一)。
(1)课件出示:把4支铅笔放进3个笔筒中,可以怎么放?有几种情况?
(2)引导学生小组合作用自己的方法解决问题。(鼓励学生用放一放、画一画、说一说等不同的方法解决)
(3)组织学生交流、汇报。
2.教师精讲点拨。
(1)强调:不管怎样放,总有1个笔筒里至少有2支铅笔。
(2)点拨:这类问题有两种思考方法:枚举法和假设法。(重点指导、示范用假设法解题的过程)
3.总结:“鸽巢原理 (一) ”。
把m个物体任意分放进n个抽屉中(m>n,m和n是非0自然数),那么一定有1个抽屉中至少放进了2个物体。
1.(1)观看课件出示的题目,读题,分析题意。
(2)小组合作,尝试用不同的方法进行解答。
①用实物操作。
②画图法。
③数的分解法。
……
(3)小组选代表进行汇报:有四种情况,分别是4支,0支,0支;3支,1支,0支;2支,2支,0支;2支,1支,1支。
2.认真倾听教师的讲解和点拨。
(1)明确:不管怎样放,总有1个笔筒里至少有2支铅笔。
(2)理解枚举和假设的思考方法,并对两种方法进行比较。
3.与教师共同归纳,得出一般性结论,理解“鸽巢原理(一)”。
3.填空。
(1)4只鸽子飞回3个鸽笼,至少有(2)只鸽子飞进同一个鸽笼。
(2)把6个球放进5个盒子里,至少有(2)个球放进同一个盒子里。
4.说一说。
(1)7只鸽子飞回到5个鸽舍,至少有2只鸽子飞回到同一个鸽舍里,为什么?
自己说一说
(2)10名同学骑9辆自行车去郊游,至少有2名同学骑同一辆自行车,为什么?
自己说一说
三、深入探究,解决问题。(15分钟)
1.课件出示教材第69页例2情境图,引导学生观察,获取数学信息。
2.引导学生小组合作,用自己喜欢的方法解决问题。(枚举法、假设法)
3.引导学生用“尽量平均分”解题,得出:物体数÷鸽巢数=商……余数,至少数=商+1。
4.尝试解决:把8本书放进3个抽屉里,总有1个抽屉里至少放进几本书?把10本书放进3个抽屉里呢?
5.总结“鸽巢原理 (二) ”。
把多于kn个的物体任意分放进n个抽屉中(k是正整数,n是非0自然数),那么一定有1个抽屉中至少放进了(k+1)个物体。
1.观察情境图,获取数学信息。
2.尝试用自己喜欢的方法解决问题,并交流放法。
3.利用平均分的关系列出除法算式,明确方法。
7÷3=2……1 2+1=3
4.讨论后用算式表示解题过程。
8÷3=2……2 2+1=3
10÷3=3……1 3+1=4
5.交流,感悟“鸽巢原理 (二) ”,并在小组内举例验证。
5.一个班级有40人,至少有几人的属相是相同的?
40÷12=3(人)……4(人)
3+1=4(人)
6. 把10只兔子放进4个兔笼,至少有几只兔子放进同一个兔笼?
10÷4=2(只)……2(只)
2+1=3(只)
三、应用新知,巩固方法。(3分钟)
1.完成教材第68页“做一做”第1,2题。
2.完成教材第69页“做一做”第1,2题。
独立完成后全班交流,并说出计算过程。
7. 体育课上,10个小朋友进行投篮练习,他们一共投进54个球。有1个小朋友至少投进(6)个球。
四、课堂小结,拓展延伸。(4分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.鸽巢原理又称抽屉原理,也称为狄利克雷原理。用它可以解决一些相当复杂甚至无从下手的问题。
3.假设法体现了鸽巢原理的最不利情况。先把待分物体平均分,如果有剩余,那么抽屉里的物品数量至少是平均分的结果再加1。
教师个人补充意见:
板书设计
鸽巢原理
物体数÷鸽巢数=商……余数
至少数=商+1
培优作业
一副扑克牌(取出两张王牌)。
一次至少要拿出多少张,才能保证有2张是相同花色的?
5张
一次至少要拿出多少张,才能保证4种花色都有?
52÷4=13(张) 13×3+1=40(张)
名师点睛
教学中,可借助具体的操作情境,引导学生利用生活经验,自主思考、猜测、验证、推理、交流,使学生在操作、思考中得出一般性的结论,体验并理解“鸽巢原理”的最基本形式。
微课设计点
教师可围绕“鸽巢原理”设计微课。
教学设计表
学科:数学 年级:六年级 册次:下 学校: 教师:
课题
鸽巢原理(P68例1、P69例2)
课型
新授课
计划学时
1
教学内容分析
例1借助把4支铅笔放进3个笔筒中的操作情境,介绍了“鸽巢原理”的最基本形式。例2介绍了另一种类型的“鸽巢问题”,即:把多于kn个的物体任意分放进n个抽屉中(k是正整数,n是非0自然数),那么一定有1个抽屉中至少放进了(k+1)个物体。
承前启后
平均分问题→鸽巢原理→应用鸽巢原理解决问题
教学目标
1.经历“鸽巢原理”的探究过程,通过观察、猜测等方法初步了解“鸽巢原理”。
2.了解“鸽巢原理”的两种形式,能用“鸽巢原理”解释相关的现象。
3.通过动手操作,提高学生的类推能力。
重难点
重点:经历“鸽巢原理”的探究过程,初步了解“鸽巢原理”的含义。
难点:掌握运用“鸽巢原理”解决简单的实际问题的方法。
化解措施
交流讨论,精讲点拨
教学设计思路
游戏导入,聚焦重点→合作交流,探究新知→深入探究,解决问题→应用新知,巩固方法→课堂小结,拓展延伸
教学准备
教具准备:PPT课件
学具准备:4支铅笔、3个笔筒
教学过程
教师活动
学生活动
同步检测
一、游戏导入,聚焦重点。(5分钟)
1.组织学生玩“抽扑克牌”游戏。
(1)准备一副扑克牌,取出大王、小王。选出5位同学,请他们任意抽取1张扑克牌并记在心里,把牌收好。
(2)教师猜测:在这5张扑克牌里,至少有2张是同一花色的。
(3)验证猜想。
(4)再次游戏。
请一名同学抽出14张牌,发现:这14张牌中至少有一对儿。
(5)课件出示:5张牌中至少有2张是同一花色的;14张牌中至少有一对儿。组织学生说一说“至少”的含义。
2.引入新课。
师:老师为什么能作出准确的判断呢?因为这个游戏中蕴含着一个数学原理,这节课我们就一起来研究这个原理。
1.游戏互动,猜想验证。
(1)明确游戏规则,各组选代表参与“抽扑克牌”游戏。
(2)与教师一起猜测结果。
(3)学生代表打开手里的扑克牌,验证教师的猜想,初步感知“至少”的含义。
(4)再次游戏,进一步理解“至少”的含义。
(5)观看课件出示的两句话,用自己的语言说一说“至少”的含义。
(“至少”是指最小的限度,最少。)
2.明确本节课的学习内容。
1.100名同学平均分成5组,每组有多少人?
100÷5=20(人)
2.30名同学去旅游,如果每4人住1间房,那么一共需要几间房?
30÷4=7(间)……2(人)
7+1=8(间)
二、合作交流,探究新知。(13分钟)
1.教学例1,探究鸽巢原理(一)。
(1)课件出示:把4支铅笔放进3个笔筒中,可以怎么放?有几种情况?
(2)引导学生小组合作用自己的方法解决问题。(鼓励学生用放一放、画一画、说一说等不同的方法解决)
(3)组织学生交流、汇报。
2.教师精讲点拨。
(1)强调:不管怎样放,总有1个笔筒里至少有2支铅笔。
(2)点拨:这类问题有两种思考方法:枚举法和假设法。(重点指导、示范用假设法解题的过程)
3.总结:“鸽巢原理 (一) ”。
把m个物体任意分放进n个抽屉中(m>n,m和n是非0自然数),那么一定有1个抽屉中至少放进了2个物体。
1.(1)观看课件出示的题目,读题,分析题意。
(2)小组合作,尝试用不同的方法进行解答。
①用实物操作。
②画图法。
③数的分解法。
……
(3)小组选代表进行汇报:有四种情况,分别是4支,0支,0支;3支,1支,0支;2支,2支,0支;2支,1支,1支。
2.认真倾听教师的讲解和点拨。
(1)明确:不管怎样放,总有1个笔筒里至少有2支铅笔。
(2)理解枚举和假设的思考方法,并对两种方法进行比较。
3.与教师共同归纳,得出一般性结论,理解“鸽巢原理(一)”。
3.填空。
(1)4只鸽子飞回3个鸽笼,至少有(2)只鸽子飞进同一个鸽笼。
(2)把6个球放进5个盒子里,至少有(2)个球放进同一个盒子里。
4.说一说。
(1)7只鸽子飞回到5个鸽舍,至少有2只鸽子飞回到同一个鸽舍里,为什么?
自己说一说
(2)10名同学骑9辆自行车去郊游,至少有2名同学骑同一辆自行车,为什么?
自己说一说
三、深入探究,解决问题。(15分钟)
1.课件出示教材第69页例2情境图,引导学生观察,获取数学信息。
2.引导学生小组合作,用自己喜欢的方法解决问题。(枚举法、假设法)
3.引导学生用“尽量平均分”解题,得出:物体数÷鸽巢数=商……余数,至少数=商+1。
4.尝试解决:把8本书放进3个抽屉里,总有1个抽屉里至少放进几本书?把10本书放进3个抽屉里呢?
5.总结“鸽巢原理 (二) ”。
把多于kn个的物体任意分放进n个抽屉中(k是正整数,n是非0自然数),那么一定有1个抽屉中至少放进了(k+1)个物体。
1.观察情境图,获取数学信息。
2.尝试用自己喜欢的方法解决问题,并交流放法。
3.利用平均分的关系列出除法算式,明确方法。
7÷3=2……1 2+1=3
4.讨论后用算式表示解题过程。
8÷3=2……2 2+1=3
10÷3=3……1 3+1=4
5.交流,感悟“鸽巢原理 (二) ”,并在小组内举例验证。
5.一个班级有40人,至少有几人的属相是相同的?
40÷12=3(人)……4(人)
3+1=4(人)
6. 把10只兔子放进4个兔笼,至少有几只兔子放进同一个兔笼?
10÷4=2(只)……2(只)
2+1=3(只)
三、应用新知,巩固方法。(3分钟)
1.完成教材第68页“做一做”第1,2题。
2.完成教材第69页“做一做”第1,2题。
独立完成后全班交流,并说出计算过程。
7. 体育课上,10个小朋友进行投篮练习,他们一共投进54个球。有1个小朋友至少投进(6)个球。
四、课堂小结,拓展延伸。(4分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.鸽巢原理又称抽屉原理,也称为狄利克雷原理。用它可以解决一些相当复杂甚至无从下手的问题。
3.假设法体现了鸽巢原理的最不利情况。先把待分物体平均分,如果有剩余,那么抽屉里的物品数量至少是平均分的结果再加1。
教师个人补充意见:
板书设计
鸽巢原理
物体数÷鸽巢数=商……余数
至少数=商+1
培优作业
一副扑克牌(取出两张王牌)。
一次至少要拿出多少张,才能保证有2张是相同花色的?
5张
一次至少要拿出多少张,才能保证4种花色都有?
52÷4=13(张) 13×3+1=40(张)
名师点睛
教学中,可借助具体的操作情境,引导学生利用生活经验,自主思考、猜测、验证、推理、交流,使学生在操作、思考中得出一般性的结论,体验并理解“鸽巢原理”的最基本形式。
微课设计点
教师可围绕“鸽巢原理”设计微课。
