江苏省南通市2018-2019学年高一下学期期末考试数学试题 Word版含解析
文档属性
| 名称 | 江苏省南通市2018-2019学年高一下学期期末考试数学试题 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 479.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-04 00:00:00 | ||
图片预览




文档简介
南通市2018-2019学年高一下学期期末调研测试
数学
一、选择题:本题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合M={x|x<0},N={x|x≤0},则( )
A. M∩N= B. MUN=R C. MN D. NM
2.函数定义域为( )
A. (一∞,0] B. [0,+∞) C. (0,+∞) D. (-∞,+∞)
3.在△ABC中,M是BC的中点.若=,=,则=( )
A. B. C. D.
4.在平面直角坐标系xoy中,已知直线l上的一点向右平移2个单位长度,再向下平移4个单位长度后,仍在该直线上,则直线l的斜率为( )
A. -2 B. - C. D. 2
5.已知函数=sinx与的图象的一个交点的横坐标为,则=( )
A. - B. - C. D.
6.下列说法正确的为
①如果两条直线同时平行于第三条直线,那么这两条直线平行;
②如果两条直线同时垂直于第三条直线,那么这两条直线平行;
③如果两条直线同时平行于一个平面,那么这两条直线平行;
④如果两条直线同时垂直于一个平面,那么这两条直线平行.( )
A. ①② B. ②③ C. ③④ D. ①④
7.从两个班级各随机抽取5名学生测量身高(单位:cm),甲班的数据为169,162,150,160,159,乙班的数据为180,160,150,150,165.据此估计甲、乙两班学生的平均身高,及方差,的关系为( )
A. , B. , C. , D. ,
8.函数的图象大致为( )
A. B. C. D.
9.△ABC的内角A,B,C的对边分别为a,b,c,若A=60°,b=10,则结合a的值解三角形有两解的为( )
A. a=8 B. a=9 C. a=10 D. a=11
10.己知函数定义在R上的周期为4的奇函数,且当0≤x≤2时,,函数,则方程的解的个数为( )
A. 4 B. 6 C. 8 D. 10
二、填空题:本题共6小题,每小题5分,共30分。
11.已知角α终边上一点P(-3,4),则sinα=____
12.已知平面向量的夹角为,,则____
13.某校共有学生1600人,其中高一年级400人.为了解各年级学生的兴趣爱好情况,用分层抽样的方法从中抽取容量为80的样本,则应抽取高一学生____人.
14.在棱长为1的正方体ABCD–A1B1C1D1中,点E是棱B1B的中点,则三棱锥D1-DEC1的体积为____.
15.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,如左下图.假定在水流量稳定的情况下,半径为3m的筒车上的每一个盛水桶都按逆时针方向作角速度为rad/min的匀速圆周运动,平面示意图如右下图,己知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点P0处,且∠P0OA=(OA//BC),则8min后该盛水筒到水面的距离为____m.
16.过点P(t,t)作圆C:(x一2)2+y2=1的两条切线,切点为A,B,若直线AB过点(2,),则t=____.
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知点O(0,0),A(2,一1),B(一4,8).
(1)若点C满足,求点C的坐标;
(2)若与垂直,求k.
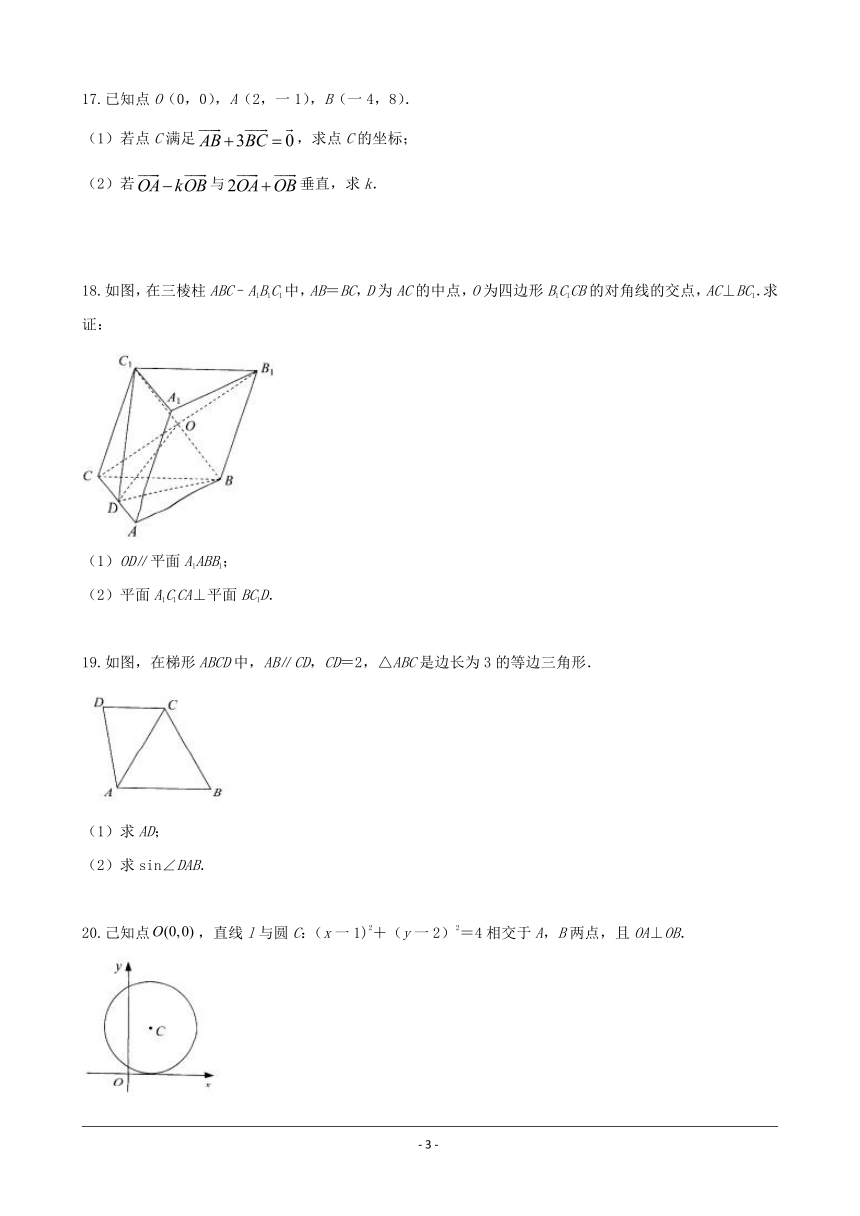
18.如图,在三棱柱ABC–A1B1C1中,AB=BC,D为AC的中点,O为四边形B1C1CB的对角线的交点,AC⊥BC1.求证:
(1)OD∥平面A1ABB1;
(2)平面A1C1CA⊥平面BC1D.
19.如图,在梯形ABCD中,AB∥CD,CD=2,△ABC是边长为3的等边三角形.
(1)求AD;
(2)求sin∠DAB.
20.己知点,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.
(1)若直线OA方程为y=一3x,求直线OB被圆C截得的弦长;
(2)若直线l过点(0,2),求l的方程.
21.已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
0
1
2
3
0
0.7
1.6
3.3
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
22.已知函数.
(1)若f(-1)=f(1),求a,并直接写出函数的单调增区间;
(2)当a≥时,是否存在实数x,使得=一?若存在,试确定这样的实数x的个数;若不存在,请说明理由.
答案与解析
一、选择题:本题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合M={x|x<0},N={x|x≤0},则( )
A. M∩N= B. MUN=R C. MN D. NM
【答案】C
【解析】
【分析】
根据具有包含关系的两个集合的交集与并集的性质求得结果.
【详解】因为,
所以有,
所以有,,
所以只有C是正确的,
故选C.
【点睛】该题考查的是有关集合的问题,涉及到的知识点有判断两集合的关系,具备包含关系的两集合的交并运算的性质,属于简单题目.
2.函数定义域为( )
A. (一∞,0] B. [0,+∞) C. (0,+∞) D. (-∞,+∞)
【答案】A
【解析】
【分析】
根据偶次根式的条件,借助于指数函数的单调性求得结果.
【详解】由题意得,解得,
所以函数的定义域是,
故选A.
【点睛】该题考查的是有关函数定义域的求解问题,属于简单题目.
3.在△ABC中,M是BC的中点.若=,=,则=( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据向量的加法的几何意义即可求得结果.
【详解】在中,M是BC的中点,
又,
所以,
故选D.
【点睛】该题考查的是有关向量的问题,涉及到的知识点有向量的加法运算,属于简单题目.
4.在平面直角坐标系xoy中,已知直线l上的一点向右平移2个单位长度,再向下平移4个单位长度后,仍在该直线上,则直线l的斜率为( )
A. -2 B. - C. D. 2
【答案】A
【解析】
【分析】
首先设出直线l上的一点,进而求得移动变换之后点,根据点在直线上,利用两点斜率坐标公式求得斜率,从而求得结果.
【详解】根据题意,设点是直线l上的一点,
将点向右平移2个单位后再向下平移4个单位得到点,
由已知有:点仍在该直线上,
所以直线的斜率,
所以直线l的斜率为,
故选A.
【点睛】该题考查的是有关直线的斜率问题,涉及到的知识点有平移变换,两点斜率坐标公式,属于简单题目.
5.已知函数=sinx与的图象的一个交点的横坐标为,则=( )
A. - B. - C. D.
【答案】B
【解析】
【分析】
首先根据题中的条件,得到,从而求得,根据题中所给的,进而求得结果.
【详解】由题意得,所以,
所以,因为,
所以,
故选B.
【点睛】该题考查的是有关三角函数的问题,涉及到的知识点有诱导公式,已知三角函数值求角,属于简单题目.
6.下列说法正确的为
①如果两条直线同时平行于第三条直线,那么这两条直线平行;
②如果两条直线同时垂直于第三条直线,那么这两条直线平行;
③如果两条直线同时平行于一个平面,那么这两条直线平行;
④如果两条直线同时垂直于一个平面,那么这两条直线平行.( )
A. ①② B. ②③ C. ③④ D. ①④
【答案】D
【解析】
【分析】
①由平行线的传递性,根据公里四得到其正确性;
②如果两条直线同时垂直于第三条直线,则两直线可以平行,可以相交,也可以异面,从而得到其错误;
③如果两条直线同时平行于一个平面,则两直线可以平行,可以相交,也可以异面从而得到其错误;
④根据线面垂直的性质得到其正确性;
从而得到正确结果.
【详解】①由平行线的传递性:平行于同一直线的两直线平行,所以正确;
②如果两条直线同时垂直于第三条直线,则两直线可以平行,可以相交,也可以异面,所以不正确;
③如果两条直线同时平行于一个平面,则两直线可以平行,可以相交,也可以异面,所以不正确;
④垂直于同一平面的两直线平行,所以正确;
所以正确的说法是①④,
故选D.
【点睛】该题考查的是有关空间立体几何的问题,涉及到的知识点有直线平行的传递性,直线的垂直关系,线面平行,线面垂直,属于简单题目.
7.从两个班级各随机抽取5名学生测量身高(单位:cm),甲班的数据为169,162,150,160,159,乙班的数据为180,160,150,150,165.据此估计甲、乙两班学生的平均身高,及方差,的关系为( )
A. , B. , C. , D. ,
【答案】C
【解析】
【分析】
利用公式求得和,从而得到和的大小,观察两组数据的波动程度,可以得到与的大小,从而求得结果.
【详解】甲班平均身高,
乙班平均身高,
所以,
方差表示数据的波动,当波动越大时,方差越大,
甲班的身高都差不多,波动比较小,而乙班身高差距则比加大,波动比较大,
所以,
故选C.
【点睛】该题考查的是有关所给数据的平均数与方差的比较大小的问题,涉及到的知识点有平均数的公式,观察数据波动程度来衡量方差的大小,属于简单题目.
8.函数的图象大致为( )
A. B. C. D.
【答案】D
【解析】
【分析】
首先判断函数的定义域,结合,从而得到为奇函数,得到函数图象关于原点对称,利用相应的自变量对应的函数值的变化趋势,从而将不满足条件的项排除,从而求得结果.
【详解】函数定义域关于原点对称,,
所以为奇函数,图象关于原点对称,所以先排除B,
当时,,排除A,
当时,,排除C,
故选D.
【点睛】该题考查的是有关函数图象的识别问题,关于图象的选择问题,可以通过函数的定义域,函数图象的对称性,函数的单调性,函数值的符号,函数图象所过的特殊点,将正确选项选出来,属于中档题目.
9.△ABC的内角A,B,C的对边分别为a,b,c,若A=60°,b=10,则结合a的值解三角形有两解的为( )
A. a=8 B. a=9 C. a=10 D. a=11
【答案】B
【解析】
【分析】
根据正弦定理得到,分情况讨论,得到正确的结果.
【详解】由正弦定理知,
由题意知,若,则,只有一解;若,则A>B,只有一解;
从而要使的值解三角形有两解,
则必有,且,即,
解得,即,因此只有B选项符合条件,
故选B.
【点睛】该题考查的是有关根据三角形的解的个数选择边长的可取值的问题,涉及到的知识点有正弦定理,属于简单题目.
10.己知函数定义在R上的周期为4的奇函数,且当0≤x≤2时,,函数,则方程的解的个数为( )
A. 4 B. 6 C. 8 D. 10
【答案】C
【解析】
【分析】
首先根据题中所给的条件,画出函数在区间上的图象,利用对称性画出区间上的图象,利用函数的周期画出函数在区间上的图象,之后在同一坐标系中画出的图象,利用两图象交点的个数求得结果.
【详解】因为函数定义在R上的周期为4的奇函数,
且当0≤x≤2时,,
所以画出函数的图象,在同一坐标系中画出的图象,如图所示:
观察图象可知两个函数图象有8个交点,其中右边3个交点,左边5个交点,所以方程有8个解,
故选C.
【点睛】该题考查的是有关方程解的个数问题,在解题的过程中,将方程解 个数转化为函数图象交点的个数,涉及到的知识点有奇函数图象的对称性,函数的周期性,属于中档题目.
二、填空题:本题共6小题,每小题5分,共30分。
11.已知角α终边上一点P(-3,4),则sinα=____
【答案】
【解析】
【分析】
根据三角函数的定义即可求解.
【详解】解:已知角a的终边经过点,
∴.
故答案为:.
【点睛】本题主要考查三角函数的定义,熟记定义,即可求解,属于基础题型.
12.已知平面向量的夹角为,,则____
【答案】1
【解析】
【分析】
利用向量数量积的定义式求解即可.
【详解】根据题意可得,
故答案是1.
【点睛】该题考查的是有关平面向量数量积的求解问题,涉及到的知识点有平面向量数量积的定义式,属于简单题目.
13.某校共有学生1600人,其中高一年级400人.为了解各年级学生的兴趣爱好情况,用分层抽样的方法从中抽取容量为80的样本,则应抽取高一学生____人.
【答案】20
【解析】
【分析】
利用分层抽样方法直接求解.
【详解】由题意,应抽取高一学生(人),
故答案是20.
【点睛】该题考查的是有关分层抽样中某层所抽个体数的问题,涉及到的知识点有分层抽样要求每个个体被抽到的概率是相等的,列式求得结果,属于简单题目.
14.在棱长为1的正方体ABCD–A1B1C1D1中,点E是棱B1B的中点,则三棱锥D1-DEC1的体积为____.
【答案】
【解析】
【分析】
首先根据题意,画出几何图形,之后将三棱锥的顶点和底面转换,利用等积法求得结果.
【详解】根据题意,画出图形,如图所示:
结合正方体的性质,以及椎体的体积公式,可以求得:
,
故答案是:.
【点睛】该题考查的是有关椎体体积的计算问题,涉及到的知识点有等级法求三棱锥的体积,椎体体积公式,属于简单题目.
15.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,如左下图.假定在水流量稳定的情况下,半径为3m的筒车上的每一个盛水桶都按逆时针方向作角速度为rad/min的匀速圆周运动,平面示意图如右下图,己知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点P0处,且∠P0OA=(OA//BC),则8min后该盛水筒到水面的距离为____m.
【答案】
【解析】
【分析】
由题意可得转动8分钟之后盛水桶所转过的角度,从而确定出其所在的位置,结合三角函数的有关知识,求得点P到水面的距离.
【详解】根据题意可得,8分钟后盛水桶所转过的角为,
而除去一圈,,
所以转8分钟之后P0所转到的位置P满足 ,
所以点P到水面距离,
故答案是:.
【点睛】该题考查的是有关三角函数的应用问题,涉及到的知识点有角速度的应用,三角函数的定义式,属于简单题目.
16.过点P(t,t)作圆C:(x一2)2+y2=1的两条切线,切点为A,B,若直线AB过点(2,),则t=____.
【答案】8
【解析】
【分析】
根据圆的方程得到圆C的圆心坐标和圆的半径,从而求得以为直径的圆的方程,将两圆方程相减,求得两圆公共弦所在直线的方程,根据直线过点的条件,得到关于的等量关系式,最后求得结果.
【详解】因为圆C:的圆心为,,
所以以为直径的圆的方程为,
即,
可得:,
即直线的方程为,
因为直线过点,
所以,解得,
故答案是:8.
【点睛】该题考查的是有关圆的问题,涉及到的知识点有以某条线段为直径的圆的方程,两圆的公共弦所在直线的方程,点在直线上的条件,属于中档题目.
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知点O(0,0),A(2,一1),B(一4,8).
(1)若点C满足,求点C的坐标;
(2)若与垂直,求k.
【答案】(1);(2).
【解析】
【分析】
(1)设出C点的坐标,利用终点减起点坐标求得和的坐标,利用向量运算坐标公式,得到满足的条件求得结果;
(2)利用向量坐标运算公式求得,,利用向量垂直的条件,得到等量关系式,求得结果.
【详解】(1)因为,,所以.
设点C的坐标为,则.
由,得
解得,,
所以点C的坐标为.
(2),,
因为与垂直,
所以,解得.
【点睛】该题考查的是有关向量的问题,涉及到的知识点有向量坐标运算公式及法则,向量垂直的条件,数量积坐标公式,属于简单题目.
18.如图,在三棱柱ABC–A1B1C1中,AB=BC,D为AC的中点,O为四边形B1C1CB的对角线的交点,AC⊥BC1.求证:
(1)OD∥平面A1ABB1;
(2)平面A1C1CA⊥平面BC1D.
【答案】(1)详见解析;(2)详见解析.
【解析】
【分析】
(1)连结,根据三棱柱的性质,得到四边形为平行四边形,从而得到O为的中点,结合题的条件,得到,利用线面平行的判定定理证得结果;
(2)利用等腰三角形,得到,又因为,之后应用线面垂直的判定定理证得平面,再应用面面垂直的判定定理证得平面平面.
【详解】证明:(1)连结,在三棱柱中,
四边形为平行四边形,
从而O为平行四边形对角线的交点,所以O为的中点.
又D是AC的中点,从而在,中,有,
又平面,平面,
所以平面.
(2)在中,因为,D为AC的中点,
所以.
又因为,
,,平面,
所以平面,
因为平面,
所以平面平面.
【点睛】该题考查的是有关立体几何的问题,涉及到的知识点有线面平行的判定,面面垂直的判定,属于简单题目.
19.如图,在梯形ABCD中,AB∥CD,CD=2,△ABC是边长为3的等边三角形.
(1)求AD;
(2)求sin∠DAB.
【答案】(1);(2).
【解析】
【分析】
(1)利用平行线的性质以及题的条件,得到,,利用余弦定理求得的长度;
(2)法1:在中,应用正弦定理求得的值,利用同旁内角互补以及诱导公式求得sin∠DAB的值;法2:利用余弦定理求得的值,利用同角三角函数关系求得,利用正弦和角公式求得sin∠DAB的值.
【详解】(1)在梯形ABCD中,因为,是边长为3的等边三角形,
所以,.
在中,由余弦定理,得
,
所以.
(2)法1:在中,由正弦定理,得,
结合(1)知,.
因为,所以.
从而.
法2:在中,由余弦定理,得
结合(1)知,.
从而.
所以
.
【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有平行线的性质,余弦定理,正弦定理,同角三角函数关系式,属于简单题目.
20.己知点,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.
(1)若直线OA方程为y=一3x,求直线OB被圆C截得的弦长;
(2)若直线l过点(0,2),求l的方程.
【答案】(1);(2).
【解析】
【分析】
(1)根据题意,求得直线OB的方程,利用点到直线的距离公式求得圆心到直线OB的距离,之后应用圆中的特殊三角形,求得弦长;
(2)根据题意,可判断直线的斜率是存在的,设出其方程,与圆的方程联立,得到两根和与两根积,根据OA⊥OB,利用向量数量积等于零得到所满足的等量关系式,求得结果.
【详解】(1)因为直线OA的方程为,,
所以直线OB的方程.
从而圆心到直线OB的距离为:
所以直线OB被团C截得的弦长为:.
(2)依题意,直线l斜率必存在,不妨设其为k,则l的方程为,
又设,.
由得,
所以,.
从而.
所以.
因为,所以,即,解得.
所以l的方程为.
【点睛】该题考查的是有关直线与圆的问题,涉及到的知识点有两直线垂直的条件,直线被圆截得的弦长,直线方程的求解,属于简单题目.
21.已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
0
1
2
3
0
0.7
1.6
3.3
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
【答案】(1)选择函数模型,函数解析式为;(2)以1百公里/小时航行时可使AB段的航行费用最少,且最少航行费用为2.1万元.
【解析】
【分析】
(1)对题中所给的三个函数解析式进行分析,对应其性质,结合题中所给的条件,作出正确的选择,之后利用待定系数法求得解析式,得出结果;
(2)根据题意,列出函数解析式,之后应用配方法求得最值,得到结果.
【详解】(1)若选择函数模型,则该函数在上为单调减函数,
这与试验数据相矛盾,所以不选择该函数模型.
若选择函数模型,须,这与试验数据在时有意义矛盾,
所以不选择该函数模型.
从而只能选择函数模型,由试验数据得,
,即,解得
故所求函数解析式为:.
(2)设超级快艇在AB段的航行费用为y(万元),
则所需时间为(小时),其中,
结合(1)知,
所以当时,.
答:当该超级快艇以1百公里/小时航行时可使AB段的航行费用最少,且最少航行费用为2.1万元.
【点睛】该题考查的是有关函数的应用题,涉及到的知识点有函数模型的正确选择,等量关系式的建立,配方法求二次式的最值,属于简单题目.
22.已知函数.
(1)若f(-1)=f(1),求a,并直接写出函数的单调增区间;
(2)当a≥时,是否存在实数x,使得=一?若存在,试确定这样的实数x的个数;若不存在,请说明理由.
【答案】(1),单调增区间为,;(2)2个.
【解析】
【分析】
(1)首先根据题中所给的函数解析式,利用,得到所满足的等量关系式,求得的值,从而得到函数的解析式,进而求得函数的单调增区间;
(2)根据条件,结合函数解析式,分类讨论,分析性质,
【详解】(1)由,得,解得.
此时,函数
所以函数的单调增区间为,.
(2)显然,不满足;
若,则,由,得,
化简,得,无解:
若,则,由,得,
化简,得.
令,.
当时,;
下面证明函数在上是单调增函数.
任取,且,
则
由于
,
所以,即,故在上是单调增函数。
因为,,
所以,又函数的图象不间断,所以函数在上有且只有一个零点.
即当时,有且只有一个实数x满足.
因为当满足时,实数也一定满足,即满足的根成对出现(互为相反数);
所以,所有满足的实数x的个数为2.
【点睛】该题考查的是有关函数解析式中参数的确定,分段函数的单调区间的求解,是否存在类问题的求解思路,分类讨论思想的应用,属于较难题目.
数学
一、选择题:本题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合M={x|x<0},N={x|x≤0},则( )
A. M∩N= B. MUN=R C. MN D. NM
2.函数定义域为( )
A. (一∞,0] B. [0,+∞) C. (0,+∞) D. (-∞,+∞)
3.在△ABC中,M是BC的中点.若=,=,则=( )
A. B. C. D.
4.在平面直角坐标系xoy中,已知直线l上的一点向右平移2个单位长度,再向下平移4个单位长度后,仍在该直线上,则直线l的斜率为( )
A. -2 B. - C. D. 2
5.已知函数=sinx与的图象的一个交点的横坐标为,则=( )
A. - B. - C. D.
6.下列说法正确的为
①如果两条直线同时平行于第三条直线,那么这两条直线平行;
②如果两条直线同时垂直于第三条直线,那么这两条直线平行;
③如果两条直线同时平行于一个平面,那么这两条直线平行;
④如果两条直线同时垂直于一个平面,那么这两条直线平行.( )
A. ①② B. ②③ C. ③④ D. ①④
7.从两个班级各随机抽取5名学生测量身高(单位:cm),甲班的数据为169,162,150,160,159,乙班的数据为180,160,150,150,165.据此估计甲、乙两班学生的平均身高,及方差,的关系为( )
A. , B. , C. , D. ,
8.函数的图象大致为( )
A. B. C. D.
9.△ABC的内角A,B,C的对边分别为a,b,c,若A=60°,b=10,则结合a的值解三角形有两解的为( )
A. a=8 B. a=9 C. a=10 D. a=11
10.己知函数定义在R上的周期为4的奇函数,且当0≤x≤2时,,函数,则方程的解的个数为( )
A. 4 B. 6 C. 8 D. 10
二、填空题:本题共6小题,每小题5分,共30分。
11.已知角α终边上一点P(-3,4),则sinα=____
12.已知平面向量的夹角为,,则____
13.某校共有学生1600人,其中高一年级400人.为了解各年级学生的兴趣爱好情况,用分层抽样的方法从中抽取容量为80的样本,则应抽取高一学生____人.
14.在棱长为1的正方体ABCD–A1B1C1D1中,点E是棱B1B的中点,则三棱锥D1-DEC1的体积为____.
15.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,如左下图.假定在水流量稳定的情况下,半径为3m的筒车上的每一个盛水桶都按逆时针方向作角速度为rad/min的匀速圆周运动,平面示意图如右下图,己知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点P0处,且∠P0OA=(OA//BC),则8min后该盛水筒到水面的距离为____m.
16.过点P(t,t)作圆C:(x一2)2+y2=1的两条切线,切点为A,B,若直线AB过点(2,),则t=____.
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知点O(0,0),A(2,一1),B(一4,8).
(1)若点C满足,求点C的坐标;
(2)若与垂直,求k.
18.如图,在三棱柱ABC–A1B1C1中,AB=BC,D为AC的中点,O为四边形B1C1CB的对角线的交点,AC⊥BC1.求证:
(1)OD∥平面A1ABB1;
(2)平面A1C1CA⊥平面BC1D.
19.如图,在梯形ABCD中,AB∥CD,CD=2,△ABC是边长为3的等边三角形.
(1)求AD;
(2)求sin∠DAB.
20.己知点,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.
(1)若直线OA方程为y=一3x,求直线OB被圆C截得的弦长;
(2)若直线l过点(0,2),求l的方程.
21.已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
0
1
2
3
0
0.7
1.6
3.3
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
22.已知函数.
(1)若f(-1)=f(1),求a,并直接写出函数的单调增区间;
(2)当a≥时,是否存在实数x,使得=一?若存在,试确定这样的实数x的个数;若不存在,请说明理由.
答案与解析
一、选择题:本题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合M={x|x<0},N={x|x≤0},则( )
A. M∩N= B. MUN=R C. MN D. NM
【答案】C
【解析】
【分析】
根据具有包含关系的两个集合的交集与并集的性质求得结果.
【详解】因为,
所以有,
所以有,,
所以只有C是正确的,
故选C.
【点睛】该题考查的是有关集合的问题,涉及到的知识点有判断两集合的关系,具备包含关系的两集合的交并运算的性质,属于简单题目.
2.函数定义域为( )
A. (一∞,0] B. [0,+∞) C. (0,+∞) D. (-∞,+∞)
【答案】A
【解析】
【分析】
根据偶次根式的条件,借助于指数函数的单调性求得结果.
【详解】由题意得,解得,
所以函数的定义域是,
故选A.
【点睛】该题考查的是有关函数定义域的求解问题,属于简单题目.
3.在△ABC中,M是BC的中点.若=,=,则=( )
A. B. C. D.
【答案】D
【解析】
【分析】
根据向量的加法的几何意义即可求得结果.
【详解】在中,M是BC的中点,
又,
所以,
故选D.
【点睛】该题考查的是有关向量的问题,涉及到的知识点有向量的加法运算,属于简单题目.
4.在平面直角坐标系xoy中,已知直线l上的一点向右平移2个单位长度,再向下平移4个单位长度后,仍在该直线上,则直线l的斜率为( )
A. -2 B. - C. D. 2
【答案】A
【解析】
【分析】
首先设出直线l上的一点,进而求得移动变换之后点,根据点在直线上,利用两点斜率坐标公式求得斜率,从而求得结果.
【详解】根据题意,设点是直线l上的一点,
将点向右平移2个单位后再向下平移4个单位得到点,
由已知有:点仍在该直线上,
所以直线的斜率,
所以直线l的斜率为,
故选A.
【点睛】该题考查的是有关直线的斜率问题,涉及到的知识点有平移变换,两点斜率坐标公式,属于简单题目.
5.已知函数=sinx与的图象的一个交点的横坐标为,则=( )
A. - B. - C. D.
【答案】B
【解析】
【分析】
首先根据题中的条件,得到,从而求得,根据题中所给的,进而求得结果.
【详解】由题意得,所以,
所以,因为,
所以,
故选B.
【点睛】该题考查的是有关三角函数的问题,涉及到的知识点有诱导公式,已知三角函数值求角,属于简单题目.
6.下列说法正确的为
①如果两条直线同时平行于第三条直线,那么这两条直线平行;
②如果两条直线同时垂直于第三条直线,那么这两条直线平行;
③如果两条直线同时平行于一个平面,那么这两条直线平行;
④如果两条直线同时垂直于一个平面,那么这两条直线平行.( )
A. ①② B. ②③ C. ③④ D. ①④
【答案】D
【解析】
【分析】
①由平行线的传递性,根据公里四得到其正确性;
②如果两条直线同时垂直于第三条直线,则两直线可以平行,可以相交,也可以异面,从而得到其错误;
③如果两条直线同时平行于一个平面,则两直线可以平行,可以相交,也可以异面从而得到其错误;
④根据线面垂直的性质得到其正确性;
从而得到正确结果.
【详解】①由平行线的传递性:平行于同一直线的两直线平行,所以正确;
②如果两条直线同时垂直于第三条直线,则两直线可以平行,可以相交,也可以异面,所以不正确;
③如果两条直线同时平行于一个平面,则两直线可以平行,可以相交,也可以异面,所以不正确;
④垂直于同一平面的两直线平行,所以正确;
所以正确的说法是①④,
故选D.
【点睛】该题考查的是有关空间立体几何的问题,涉及到的知识点有直线平行的传递性,直线的垂直关系,线面平行,线面垂直,属于简单题目.
7.从两个班级各随机抽取5名学生测量身高(单位:cm),甲班的数据为169,162,150,160,159,乙班的数据为180,160,150,150,165.据此估计甲、乙两班学生的平均身高,及方差,的关系为( )
A. , B. , C. , D. ,
【答案】C
【解析】
【分析】
利用公式求得和,从而得到和的大小,观察两组数据的波动程度,可以得到与的大小,从而求得结果.
【详解】甲班平均身高,
乙班平均身高,
所以,
方差表示数据的波动,当波动越大时,方差越大,
甲班的身高都差不多,波动比较小,而乙班身高差距则比加大,波动比较大,
所以,
故选C.
【点睛】该题考查的是有关所给数据的平均数与方差的比较大小的问题,涉及到的知识点有平均数的公式,观察数据波动程度来衡量方差的大小,属于简单题目.
8.函数的图象大致为( )
A. B. C. D.
【答案】D
【解析】
【分析】
首先判断函数的定义域,结合,从而得到为奇函数,得到函数图象关于原点对称,利用相应的自变量对应的函数值的变化趋势,从而将不满足条件的项排除,从而求得结果.
【详解】函数定义域关于原点对称,,
所以为奇函数,图象关于原点对称,所以先排除B,
当时,,排除A,
当时,,排除C,
故选D.
【点睛】该题考查的是有关函数图象的识别问题,关于图象的选择问题,可以通过函数的定义域,函数图象的对称性,函数的单调性,函数值的符号,函数图象所过的特殊点,将正确选项选出来,属于中档题目.
9.△ABC的内角A,B,C的对边分别为a,b,c,若A=60°,b=10,则结合a的值解三角形有两解的为( )
A. a=8 B. a=9 C. a=10 D. a=11
【答案】B
【解析】
【分析】
根据正弦定理得到,分情况讨论,得到正确的结果.
【详解】由正弦定理知,
由题意知,若,则,只有一解;若,则A>B,只有一解;
从而要使的值解三角形有两解,
则必有,且,即,
解得,即,因此只有B选项符合条件,
故选B.
【点睛】该题考查的是有关根据三角形的解的个数选择边长的可取值的问题,涉及到的知识点有正弦定理,属于简单题目.
10.己知函数定义在R上的周期为4的奇函数,且当0≤x≤2时,,函数,则方程的解的个数为( )
A. 4 B. 6 C. 8 D. 10
【答案】C
【解析】
【分析】
首先根据题中所给的条件,画出函数在区间上的图象,利用对称性画出区间上的图象,利用函数的周期画出函数在区间上的图象,之后在同一坐标系中画出的图象,利用两图象交点的个数求得结果.
【详解】因为函数定义在R上的周期为4的奇函数,
且当0≤x≤2时,,
所以画出函数的图象,在同一坐标系中画出的图象,如图所示:
观察图象可知两个函数图象有8个交点,其中右边3个交点,左边5个交点,所以方程有8个解,
故选C.
【点睛】该题考查的是有关方程解的个数问题,在解题的过程中,将方程解 个数转化为函数图象交点的个数,涉及到的知识点有奇函数图象的对称性,函数的周期性,属于中档题目.
二、填空题:本题共6小题,每小题5分,共30分。
11.已知角α终边上一点P(-3,4),则sinα=____
【答案】
【解析】
【分析】
根据三角函数的定义即可求解.
【详解】解:已知角a的终边经过点,
∴.
故答案为:.
【点睛】本题主要考查三角函数的定义,熟记定义,即可求解,属于基础题型.
12.已知平面向量的夹角为,,则____
【答案】1
【解析】
【分析】
利用向量数量积的定义式求解即可.
【详解】根据题意可得,
故答案是1.
【点睛】该题考查的是有关平面向量数量积的求解问题,涉及到的知识点有平面向量数量积的定义式,属于简单题目.
13.某校共有学生1600人,其中高一年级400人.为了解各年级学生的兴趣爱好情况,用分层抽样的方法从中抽取容量为80的样本,则应抽取高一学生____人.
【答案】20
【解析】
【分析】
利用分层抽样方法直接求解.
【详解】由题意,应抽取高一学生(人),
故答案是20.
【点睛】该题考查的是有关分层抽样中某层所抽个体数的问题,涉及到的知识点有分层抽样要求每个个体被抽到的概率是相等的,列式求得结果,属于简单题目.
14.在棱长为1的正方体ABCD–A1B1C1D1中,点E是棱B1B的中点,则三棱锥D1-DEC1的体积为____.
【答案】
【解析】
【分析】
首先根据题意,画出几何图形,之后将三棱锥的顶点和底面转换,利用等积法求得结果.
【详解】根据题意,画出图形,如图所示:
结合正方体的性质,以及椎体的体积公式,可以求得:
,
故答案是:.
【点睛】该题考查的是有关椎体体积的计算问题,涉及到的知识点有等级法求三棱锥的体积,椎体体积公式,属于简单题目.
15.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,如左下图.假定在水流量稳定的情况下,半径为3m的筒车上的每一个盛水桶都按逆时针方向作角速度为rad/min的匀速圆周运动,平面示意图如右下图,己知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点P0处,且∠P0OA=(OA//BC),则8min后该盛水筒到水面的距离为____m.
【答案】
【解析】
【分析】
由题意可得转动8分钟之后盛水桶所转过的角度,从而确定出其所在的位置,结合三角函数的有关知识,求得点P到水面的距离.
【详解】根据题意可得,8分钟后盛水桶所转过的角为,
而除去一圈,,
所以转8分钟之后P0所转到的位置P满足 ,
所以点P到水面距离,
故答案是:.
【点睛】该题考查的是有关三角函数的应用问题,涉及到的知识点有角速度的应用,三角函数的定义式,属于简单题目.
16.过点P(t,t)作圆C:(x一2)2+y2=1的两条切线,切点为A,B,若直线AB过点(2,),则t=____.
【答案】8
【解析】
【分析】
根据圆的方程得到圆C的圆心坐标和圆的半径,从而求得以为直径的圆的方程,将两圆方程相减,求得两圆公共弦所在直线的方程,根据直线过点的条件,得到关于的等量关系式,最后求得结果.
【详解】因为圆C:的圆心为,,
所以以为直径的圆的方程为,
即,
可得:,
即直线的方程为,
因为直线过点,
所以,解得,
故答案是:8.
【点睛】该题考查的是有关圆的问题,涉及到的知识点有以某条线段为直径的圆的方程,两圆的公共弦所在直线的方程,点在直线上的条件,属于中档题目.
三、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知点O(0,0),A(2,一1),B(一4,8).
(1)若点C满足,求点C的坐标;
(2)若与垂直,求k.
【答案】(1);(2).
【解析】
【分析】
(1)设出C点的坐标,利用终点减起点坐标求得和的坐标,利用向量运算坐标公式,得到满足的条件求得结果;
(2)利用向量坐标运算公式求得,,利用向量垂直的条件,得到等量关系式,求得结果.
【详解】(1)因为,,所以.
设点C的坐标为,则.
由,得
解得,,
所以点C的坐标为.
(2),,
因为与垂直,
所以,解得.
【点睛】该题考查的是有关向量的问题,涉及到的知识点有向量坐标运算公式及法则,向量垂直的条件,数量积坐标公式,属于简单题目.
18.如图,在三棱柱ABC–A1B1C1中,AB=BC,D为AC的中点,O为四边形B1C1CB的对角线的交点,AC⊥BC1.求证:
(1)OD∥平面A1ABB1;
(2)平面A1C1CA⊥平面BC1D.
【答案】(1)详见解析;(2)详见解析.
【解析】
【分析】
(1)连结,根据三棱柱的性质,得到四边形为平行四边形,从而得到O为的中点,结合题的条件,得到,利用线面平行的判定定理证得结果;
(2)利用等腰三角形,得到,又因为,之后应用线面垂直的判定定理证得平面,再应用面面垂直的判定定理证得平面平面.
【详解】证明:(1)连结,在三棱柱中,
四边形为平行四边形,
从而O为平行四边形对角线的交点,所以O为的中点.
又D是AC的中点,从而在,中,有,
又平面,平面,
所以平面.
(2)在中,因为,D为AC的中点,
所以.
又因为,
,,平面,
所以平面,
因为平面,
所以平面平面.
【点睛】该题考查的是有关立体几何的问题,涉及到的知识点有线面平行的判定,面面垂直的判定,属于简单题目.
19.如图,在梯形ABCD中,AB∥CD,CD=2,△ABC是边长为3的等边三角形.
(1)求AD;
(2)求sin∠DAB.
【答案】(1);(2).
【解析】
【分析】
(1)利用平行线的性质以及题的条件,得到,,利用余弦定理求得的长度;
(2)法1:在中,应用正弦定理求得的值,利用同旁内角互补以及诱导公式求得sin∠DAB的值;法2:利用余弦定理求得的值,利用同角三角函数关系求得,利用正弦和角公式求得sin∠DAB的值.
【详解】(1)在梯形ABCD中,因为,是边长为3的等边三角形,
所以,.
在中,由余弦定理,得
,
所以.
(2)法1:在中,由正弦定理,得,
结合(1)知,.
因为,所以.
从而.
法2:在中,由余弦定理,得
结合(1)知,.
从而.
所以
.
【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有平行线的性质,余弦定理,正弦定理,同角三角函数关系式,属于简单题目.
20.己知点,直线l与圆C:(x一1)2+(y一2)2=4相交于A,B两点,且OA⊥OB.
(1)若直线OA方程为y=一3x,求直线OB被圆C截得的弦长;
(2)若直线l过点(0,2),求l的方程.
【答案】(1);(2).
【解析】
【分析】
(1)根据题意,求得直线OB的方程,利用点到直线的距离公式求得圆心到直线OB的距离,之后应用圆中的特殊三角形,求得弦长;
(2)根据题意,可判断直线的斜率是存在的,设出其方程,与圆的方程联立,得到两根和与两根积,根据OA⊥OB,利用向量数量积等于零得到所满足的等量关系式,求得结果.
【详解】(1)因为直线OA的方程为,,
所以直线OB的方程.
从而圆心到直线OB的距离为:
所以直线OB被团C截得的弦长为:.
(2)依题意,直线l斜率必存在,不妨设其为k,则l的方程为,
又设,.
由得,
所以,.
从而.
所以.
因为,所以,即,解得.
所以l的方程为.
【点睛】该题考查的是有关直线与圆的问题,涉及到的知识点有两直线垂直的条件,直线被圆截得的弦长,直线方程的求解,属于简单题目.
21.已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
0
1
2
3
0
0.7
1.6
3.3
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
【答案】(1)选择函数模型,函数解析式为;(2)以1百公里/小时航行时可使AB段的航行费用最少,且最少航行费用为2.1万元.
【解析】
【分析】
(1)对题中所给的三个函数解析式进行分析,对应其性质,结合题中所给的条件,作出正确的选择,之后利用待定系数法求得解析式,得出结果;
(2)根据题意,列出函数解析式,之后应用配方法求得最值,得到结果.
【详解】(1)若选择函数模型,则该函数在上为单调减函数,
这与试验数据相矛盾,所以不选择该函数模型.
若选择函数模型,须,这与试验数据在时有意义矛盾,
所以不选择该函数模型.
从而只能选择函数模型,由试验数据得,
,即,解得
故所求函数解析式为:.
(2)设超级快艇在AB段的航行费用为y(万元),
则所需时间为(小时),其中,
结合(1)知,
所以当时,.
答:当该超级快艇以1百公里/小时航行时可使AB段的航行费用最少,且最少航行费用为2.1万元.
【点睛】该题考查的是有关函数的应用题,涉及到的知识点有函数模型的正确选择,等量关系式的建立,配方法求二次式的最值,属于简单题目.
22.已知函数.
(1)若f(-1)=f(1),求a,并直接写出函数的单调增区间;
(2)当a≥时,是否存在实数x,使得=一?若存在,试确定这样的实数x的个数;若不存在,请说明理由.
【答案】(1),单调增区间为,;(2)2个.
【解析】
【分析】
(1)首先根据题中所给的函数解析式,利用,得到所满足的等量关系式,求得的值,从而得到函数的解析式,进而求得函数的单调增区间;
(2)根据条件,结合函数解析式,分类讨论,分析性质,
【详解】(1)由,得,解得.
此时,函数
所以函数的单调增区间为,.
(2)显然,不满足;
若,则,由,得,
化简,得,无解:
若,则,由,得,
化简,得.
令,.
当时,;
下面证明函数在上是单调增函数.
任取,且,
则
由于
,
所以,即,故在上是单调增函数。
因为,,
所以,又函数的图象不间断,所以函数在上有且只有一个零点.
即当时,有且只有一个实数x满足.
因为当满足时,实数也一定满足,即满足的根成对出现(互为相反数);
所以,所有满足的实数x的个数为2.
【点睛】该题考查的是有关函数解析式中参数的确定,分段函数的单调区间的求解,是否存在类问题的求解思路,分类讨论思想的应用,属于较难题目.
同课章节目录
