江西省武宁一中沙田校区2018-2019学年高一下学期期末考试数学试题 Word版含解析
文档属性
| 名称 | 江西省武宁一中沙田校区2018-2019学年高一下学期期末考试数学试题 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 684.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-04 00:00:00 | ||
图片预览




文档简介
武宁一中沙田校区2018-2019下学期高一年级期末考试
数学试题
一、选择题,
1.直线 的倾斜角为( )
A. B. C. D.
2.奥林匹克会旗中央有5个互相套连的圆环,颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作,每人分得1个,则事件“甲分得红色”与“乙分得红色”是( )
A. 对立事件 B. 不可能事件
C. 互斥但不对立事件 D. 不是互斥事件
3.对于空间中的直线,以及平面,,下列说法正确的是( )
A. 若,,,则
B. 若,,,则
C. 若 ,,,则
D. 若,,,则
4.一组数据的茎叶图如图所示,则数据落在区间内的概率为( )
A. 0.2 B. 0.4 C. 0.5 D. 0.6
5.已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的平均数和方差分别为 ( )
A. B. C. D.
6.空气质量指数是反映空气质量状况的指数,指数值越小,表明空气质量越好,其对应关系如表:
指数值
0~50
51~100
101~150
151~200
201~300
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
如图是某市10月1日-20日指数变化趋势:
下列叙述错误的是( )
A. 这20天中指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
7.按照程序框图(如图)执行,第4个输出的数是( )
A. 5 B. 6 C. 7 D. 8
8.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹马进行一场比赛、齐王获胜的概率是( )
A. B. C. D.
9.为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
A. 12 B. 9 C. 8 D. 6
10.一个圆经过以下三个点,,,且圆心在轴上,则圆的标准方程为( )
A. B.
C. D.
11.若三条直线,,相交于同一点,则点到原点的距离的最小值为( )
A. B. C. D.
12.在四面体中,是边长为的等边三角形,,,,则四面体的体积为( )
A. B. C. D.
二、填空题(将答案填在答题纸上)
13.已知具有线性相关关系的两个量之间的一组数据如表:
0
1
2
3
4
2.2
4.3
4.5
6.7
且回直线方程是,则的值为____.
14.甲、乙、丙三人射击同一目标,命中目标的概率分别为,,,且彼此射击互不影响,现在三人射击该目标各一次,则目标被击中的概率为____.(用数字作答)
15.过点作圆:的两条切线,切点分别为,,则点到直线的距离为____.
16.已知,,,且,,,,.若在线段上(不含端点)存在不同的两点,使得,则实数的取值范围是___.
三、解答题.
17.从含有两件正品,和一件次品的3件产品中每次任取一件,连续取两次,求取出的两件产品中恰有一件是次品的概率.
(1)每次取出不放回;
(2)每次取出后放回.
18.(1)设直线的方程为.若直线在两坐标轴上的截距相等,求直线的方程;
(2)过直线:上的点作直线,若直线,与轴围成的三角形的面积为2,则直线的方程.
19.某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为)进行统计,按照,,,,的分组作出频率分布直方图,已知得分在,的频数分别为8,2.
(1)求样本容量和频率分布直方图中的的值;
(2)估计本次竞赛学生成绩的中位数;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在内的概率.
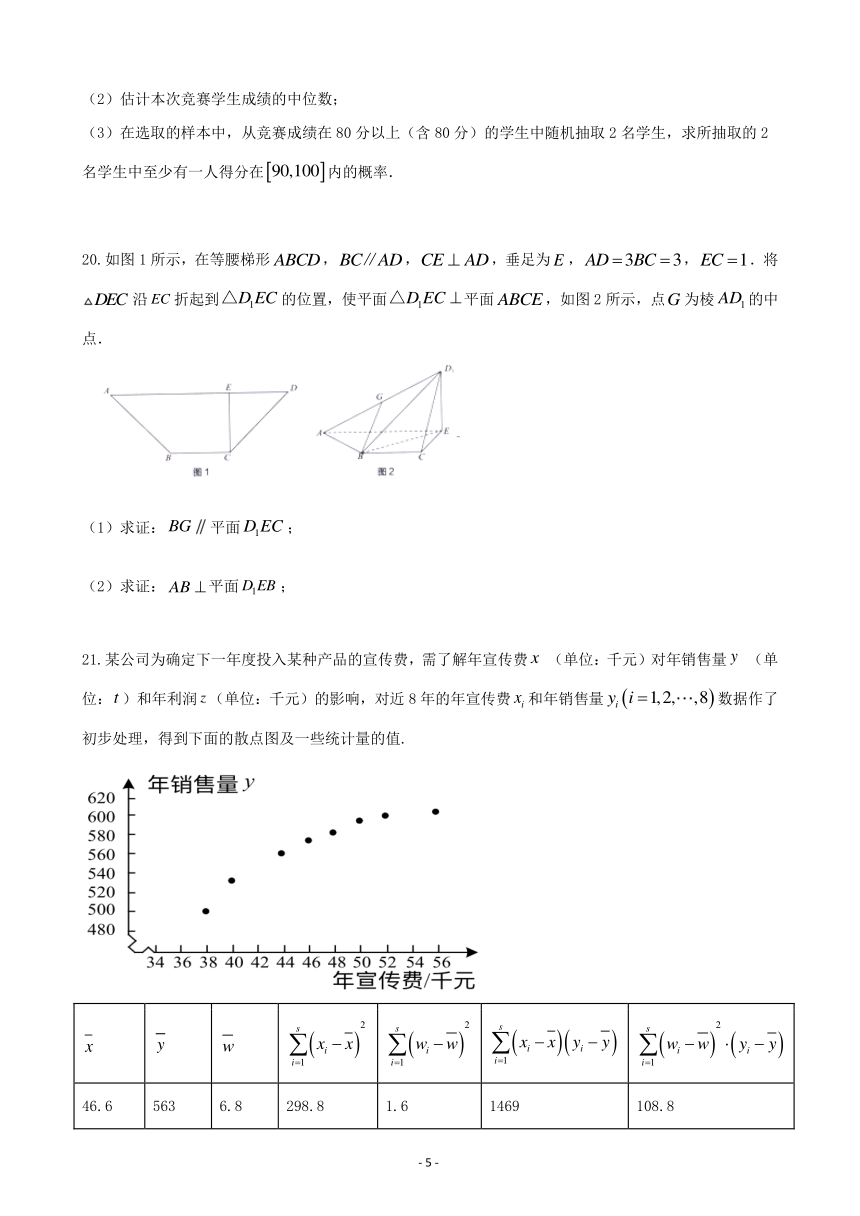
20.如图1所示,在等腰梯形,,,垂足为,,.将沿折起到的位置,使平面平面,如图2所示,点为棱的中点.
(1)求证:平面;
(2)求证:平面;
21.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 (单位:千元)对年销售量 (单位:)和年利润(单位:千元)的影响,对近8年的年宣传费和年销售量数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
563
6.8
298.8
1.6
1469
108.8
表中,
(1)根据散点图判断,与哪一个适宜作为年销售量关于年宣传费的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立关于的回归方程;
(3)以知这种产品的年利率与、的关系为.根据(2)的结果求年宣传费时,年销售量及年利润的预报值是多少?
附:对于一组数据,……,其回归线的斜率和截距的最小二乘估计分别为:,
22.已知圆:.
(1)过点向圆引切线,求切线的方程;
(2)过点任作一条直线交圆于、两点,问在轴上是否存在点,使得?若存在,求出的坐标,若不存在,请说明理由.
答案与解析
一、选择题,
1.直线 的倾斜角为( )
A. B. C. D.
【答案】A
【解析】
【分析】
直线的倾斜角就是斜率,从而求得倾斜角.
【详解】解:直线的斜率,设其倾斜角为,,
则,∴.故选:A.
【点睛】本题主要考查直线的倾斜角及斜率的关系,难度较小.
2.奥林匹克会旗中央有5个互相套连的圆环,颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作,每人分得1个,则事件“甲分得红色”与“乙分得红色”是( )
A. 对立事件 B. 不可能事件
C. 互斥但不对立事件 D. 不是互斥事件
【答案】C
【解析】
甲、乙不能同时得到红色,因而这两个事件是互斥事件;又甲、乙可能都得不到红色,即“甲或乙分得红色”的事件不是必然事件,故这两个事件不是对立事件.选C.
3.对于空间中的直线,以及平面,,下列说法正确的是( )
A. 若,,,则
B. 若,,,则
C. 若 ,,,则
D. 若,,,则
【答案】D
【解析】
【分析】
根据空间直线和平面的位置关系对四个选项逐一排除,由此确定正确的选项
【详解】对于A选项,可能异面,故A错误;对于B选项,可能有,故B错误;对于C选项,的夹角不一定为90°,故C错误;因为,故,因为,故,故D正确,故选D.
【点睛】本小题主要考查空间两条直线的位置关系,考查直线和平面、平面和平面位置关系的判断,属于基础题.
4.一组数据的茎叶图如图所示,则数据落在区间内的概率为( )
A. 0.2 B. 0.4 C. 0.5 D. 0.6
【答案】D
【解析】
【分析】
根据茎叶图个原始数据落在区间内的个数,由古典概型的概率公式可得结论.
【详解】由茎叶图个原始数据,数出落在区间内的共有6个,
包括2个个个,2个30,
所以数据落在区间内的概率为,故选D.
【点睛】本题主要考查古典概型概率公式的应用,属于简单题. 在解古典概型概率题时,首先求出样本空间中基本事件的总数,其次求出概率事件中含有多少个基本事件,然后根据公式求得概率.
5.已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的平均数和方差分别为 ( )
A. B. C. D.
【答案】A
【解析】
【分析】
由中位数为5,求出x值,再利用平均数和方差公式计算即可得到答案.
【详解】∵﹣1,0,4,x,7,14中位数为5,
∴,
∴x=6,
∴这组数据的平均数是
这组数据的方差是
故选:A.
【点睛】本题考查对一组数据的中位数,平均数,方差的计算,掌握各公式是求解的关键.
6.空气质量指数是反映空气质量状况的指数,指数值越小,表明空气质量越好,其对应关系如表:
指数值
0~50
51~100
101~150
151~200
201~300
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
如图是某市10月1日-20日指数变化趋势:
下列叙述错误的是( )
A. 这20天中指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
【答案】C
【解析】
【分析】
根据所给图象,结合中位数的定义、指数与污染程度的关系以及古典概型概率公式,对四个选项逐一判断即可.
【详解】对,因为第10天与第11天指数值都略高100,所以中位数略高于100,正确;
对,中度污染及以上的有第11,13,14,15,17天,共5天占,正确;
对,由图知,前半个月中,前4天的空气质量越来越好,后11天该市的空气质量越来越差,错误;
对,由图知,10月上旬大部分指数在100以下,10月中旬大部分指数在100以上,所以正确,故选C.
【点睛】与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际问题转化为数学模型进行解答.
7.按照程序框图(如图)执行,第4个输出的数是( )
A. 5 B. 6 C. 7 D. 8
【答案】C
【解析】
【分析】
按步骤写出对应程序,从而得到答案.
【详解】解:第一次输出的,则,满足条件,然后
第二次输出的,则,满足条件,然后
第三次输出的,则,满足条件,然后
第四次输出的,则,满足条件,然后
第五次输出的,则,不满足条件,然后退出循环
故第4个输出的数是7 故选:C.
【点睛】本题主要考查算法框图,重在考查学生的计算能力和分析能力.
8.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹马进行一场比赛、齐王获胜的概率是( )
A. B. C. D.
【答案】A
【解析】
【分析】
首先求出满足 “从双方的马匹中随机选一匹马进行一场比赛” 这一条件的事件数,然后求出满足“齐王获胜”这一条件的事件数,根据古典概型公式得出结果.
【详解】解:因为双方各有3匹马,
所以“从双方的马匹中随机选一匹马进行一场比赛”的事件数为9种,
满足“齐王获胜”的这一条件的情况为:
齐王派出上等马,则获胜的事件数为3;
齐王派出中等马,则获胜的事件数为2;
齐王派出下等马,则获胜的事件数为1;
故满足“齐王获胜”这一条件的事件数为6种,
根据古典概型公式可得,齐王获胜的概率,故选A.
【点睛】本题考查了古典概型问题,解题的关键是求出满足条件的事件数,再根据古典概型的计算公式求解问题,属于基础题.
9.为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
A. 12 B. 9 C. 8 D. 6
【答案】B
【解析】
试题分析:根据题意,设阴影部分的面积为S,则正方形的面积为36,
向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,
则向正方形内随机投掷一点,其落到阴影部分概率P=;
而,则,
解可得,S=9;
考点:模拟方法估计概率
10.一个圆经过以下三个点,,,且圆心在轴上,则圆的标准方程为( )
A. B.
C. D.
【答案】D
【解析】
【分析】
根据题意设出圆心,利用圆心到三点的距离相等建立等式,从而求得标准方程.
【详解】解:设圆心坐标为,半径为,则圆的方程为,
则,解得,.
∴圆的标准方程为.
故选:D.
【点睛】本题主要考查圆的标准方程,重点找出圆心及半径是关键,难度不大.
11.若三条直线,,相交于同一点,则点到原点的距离的最小值为( )
A. B. C. D.
【答案】A
【解析】
【分析】
联立直线求得交点,找出m,n的关系,从而表示出距离得到答案.
【详解】解:联立,解得,.
∵三条直线,,相交于同一点,∴.
则点到原点的距离的最小值为原点到直线的距离.
故选:A.
【点睛】本题主要考查学生的计算能力,以及对点线距的掌握情况,难度不大.
12.在四面体中,是边长为的等边三角形,,,,则四面体的体积为( )
A. B. C. D.
【答案】C
【解析】
【分析】
把四面体补成如图所示的三棱锥,其中,可以证明平面且、均为直角三角形,通过计算可得.
【详解】如图,延长至,使得,连接,
因为,故为等腰三角形,
又,故,
所以即,故,
因为,所以,所以,
因,平面,平面,
所以平面,
所以,
因为的中点,所以,
因为,故为直角三角形,
所以,
又,而,故即为直角三角形,
所以,所以,故选C.
【点睛】不规则三棱锥的体积的计算,应尽量找寻其高,如果高难以确定,则可以把给定的几何体补成容易计算体积的几何体,注意补体时利用已有的垂直关系.
二、填空题(将答案填在答题纸上)
13.已知具有线性相关关系的两个量之间的一组数据如表:
0
1
2
3
4
2.2
4.3
4.5
6.7
且回直线方程是,则的值为____.
【答案】4.8
【解析】
【分析】
求出数据中心,代入回归方程即可求出m的值.
【详解】2,.
∴0.95×2+2.6,解得m=4.8.
故答案为4.8.
【点睛】本题考查了线性回归方程的性质,属于基础题.
14.甲、乙、丙三人射击同一目标,命中目标的概率分别为,,,且彼此射击互不影响,现在三人射击该目标各一次,则目标被击中的概率为____.(用数字作答)
【答案】
【解析】
分析:根据独立事件同时发生的概率和对立事件的概率公式求解即可.
详解:由题意得,甲、乙、丙三人射击同一目标都未击中的概率为
,
所以甲、乙、丙至少一人击中的概率为,
即目标被击中的概率为.
点睛:解答概率问题的关键是认清概率的类型、选择合适的公式求解,对于含有“至多”、“至少”等词语的问题一般可根据对立事件的概率求解,可减少运算量、提高解题的效率.
15.过点作圆:的两条切线,切点分别为,,则点到直线的距离为____.
【答案】
【解析】
【分析】
根据圆的切线长定理,可知 ,设则的长度就是点到直线的距离,在中,利用相似三角形,得到比例式,可以求出,进而求出。
【详解】连接 设因为是圆的两条切线,所以
则,显然相似于
所以点到直线的距离为。
【点睛】本题考查了直线与圆的位置关系,解题中充分利用直角三角形相似是关键。
16.已知,,,且,,,,.若在线段上(不含端点)存在不同的两点,使得,则实数的取值范围是___.
【答案】
【解析】
【分析】
利用距离关系即可列出不等式,从而得到取值范围.
【详解】解:直线方程,即,由已知得且则可得到,由于,所以,则,由于则,所以,所以
解得:
【点睛】本题主要考查直线与圆位置关系的关系,利用点线距建立不等式是解题的关键,难度中档.
三、解答题.
17.从含有两件正品,和一件次品的3件产品中每次任取一件,连续取两次,求取出的两件产品中恰有一件是次品的概率.
(1)每次取出不放回;
(2)每次取出后放回.
【答案】(1)
(2)
【解析】
试题分析:
(1)由题意列出所有可能的结果,共有6种,然后结合古典概型公式可得每次取出不放回的概率为;
(2) 由题意列出所有可能的结果,共有9种,然后结合古典概型公式可得每次取出放回的概率为;
试题解析:
(1)每次取出一个,取后不放回地连续取两次,其一切可能的结果组成的基本事件有6个,即.用A表示“取出的两件中,恰好有一件次品”这一事件,则.
(2)由题意知本题是一个古典概型,试验发生包含的事件是每次取出一个,取后放回地连续取两次,其一切可能的结果组成的基本事件有9个,即:
用B表示“取出的两种中,恰好有一件次品”这一事件,则.
18.(1)设直线的方程为.若直线在两坐标轴上的截距相等,求直线的方程;
(2)过直线:上的点作直线,若直线,与轴围成的三角形的面积为2,则直线的方程.
【答案】(1) 或 (2) 或.
【解析】
【分析】
(1)表示出截距,然后建立等量关系得到答案.
(2)计算出与x,y轴的坐标,然后建立等量关系,即可得到直线方程.
【详解】解:(1)当直线过原点时,该直线在轴和轴上的截距为0,∴,方程即为.
当直线不经过原点时,截距存在且均不为0,直线方程为 ∴
∴,方程即为.综上,直线的方程为或.
(2)①若直线的斜率不存在,则直线的方程为,
直线,直线和轴围成的三角形的面积为2,符合题意;
②若直线的斜率,则直线与轴没有交点,不符合题意;
③若直线的斜率,设其方程为,令,得,依题意
有,解得,所以直线的方程为,即.
综上可知,直线的方程为或.
【点睛】本题主要考查直线的相关量的含义,截距不是距离,注意截距为0的情况。细心分析题目,难度不大.
19.某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为)进行统计,按照,,,,的分组作出频率分布直方图,已知得分在,的频数分别为8,2.
(1)求样本容量和频率分布直方图中的的值;
(2)估计本次竞赛学生成绩的中位数;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在内的概率.
【答案】(1);(2);(3).
【解析】
试题分析:(1)借助题设条件运用频率分布直方图求解;(2)借助题设条件运用频率分布直方图中提供的数据信息求解;(3)运用列举法和古典概型计算公式求解.
试题解析:
(1)由题意可知,样本容量n==50, ……………………2分
,x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030; ……………………4分
(2)设本次竞赛学生成绩的中位数为m,平均分为,
则[0.016+0.03]×10+(m﹣70)×0.040 =0.5,解得, ……………………6分
=(55×0.016+65×0.030+75×0.040+85×0.010+95×0.004]×10=70.6, ……………………8分
(3)由题意可知,分数在[80,90)内的学生有5人,记这5人分别为a1,a2,a3,a4,a5,
分数在[90,100]内的学生有2人,记这2人分别为b1,b2.抽取的2名学生的所有情况有21种,
分别为:(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a1,b1),(a1,b2),(a2,a3),
(a2,a4),(a2,a5),(a2,b1),(a2,b2),(a3,a4),(a3,a5),(a3,b1),
(a3,b2),(a4,a5),(a4,b1),(a4,b2),(a5,b1),(a5,b2),(b1,b2). ……………………10分
其中2名同学的分数都不在[90,100]内的情况有10种,分别为:
(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a2,a3),(a2,a4),(a2,a5),(a3,a4),(a3,a5),(a4,a5).
∴所抽取的2名学生中至少有一人得分在[90,100]内的概率. ……………………12分
考点:频率分布直方图、频率与频数的关系及古典概型的计算公式等有关知识的综合运用.
【易错点晴】本题以学校中数学竞赛的数学成绩的抽样统计的频率分布直方图为背景,设置了三个较为平常的数学问题.解答时一定要充分利用题设中提供的频率分布直方图所提供的数据信息,结合题设条件进行求解.第一问中求的是频率分布直方图中的未知数的值,运用该频率分布直方图时一定要注意该图的纵坐标是频率与组距的比值,这一点解题很容易被忽视.第二问中求的是中位数和平均数,求解时先依据中位数这个概念建立了方程求解,再运用平均数公式进行求解;第三问是运用简单枚举法一一列举出基本事件的所有可能和符合条件的事件的可能,最后运用古典概型的计算公式求出其概率的值.这是一道非常平常的考查基础知识和基本方法的基础题.
20.如图1所示,在等腰梯形,,,垂足为,,.将沿折起到的位置,使平面平面,如图2所示,点为棱的中点.
(1)求证:平面;
(2)求证:平面;
【答案】(1)见证明;(2)见证明
【解析】
【分析】
(1)利用线线平行可证明线面平行;
(2)利用线线垂直可证明线面垂直.
【详解】(1)证明:在图1的等腰梯形内,过作的垂线,垂足为,
∵,∴,又∵,,,
∴四边形为正方形,且,为中点.
在图2中,连结,∵点是的中点,∴.
又∵,,,平面,,平面,
∴平面平面,又∵面,∴平面;
(2)证明:∵平面平面,平面平面,,
平面,∴平面.又∵平面,∴.
又,,,满足,
∴.又,
平面;
【点睛】注意线面垂直和线面平面的判定方法,意在考查学生的理解能力和空间想象能力,难度中档.
21.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 (单位:千元)对年销售量 (单位:)和年利润(单位:千元)的影响,对近8年的年宣传费和年销售量数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
563
6.8
298.8
1.6
1469
108.8
表中,
(1)根据散点图判断,与哪一个适宜作为年销售量关于年宣传费的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立关于的回归方程;
(3)以知这种产品的年利率与、的关系为.根据(2)的结果求年宣传费时,年销售量及年利润的预报值是多少?
附:对于一组数据,……,其回归线的斜率和截距的最小二乘估计分别为:,
【答案】(1) 适宜作为年销售量关于年宣传费的回归方程类型. (2) (3)66.32
【解析】
【分析】
(1)根据图形可知选择曲线更加符合;
(2)通过最小二乘法计算即可得到回归方程;
(3)找到z和x的函数,转化为二次函数即可得到最值.
【详解】解:(1)由散点图可以判断,适宜作为年销售量关于年宣传费的回归方程类型.
(2)令,先建立关于的线性回归方程.由于
,.
所以关于线性回归方程为,
因此关于的回归方程为.
(3)(i)由(II)知,当时,年销售量的预报值
年利润的预报值.
【点睛】本题主要考查回归分析,对相关含义的理解是解决本题的关键,意在考查学生的转化能力及计算能力.
22.已知圆:.
(1)过点向圆引切线,求切线的方程;
(2)过点任作一条直线交圆于、两点,问在轴上是否存在点,使得?若存在,求出的坐标,若不存在,请说明理由.
【答案】(1) 或;(2)见解析
【解析】
【分析】
(1)通过直线与圆的位置关系相切,建立方程计算得到直线方程;
(2)将角度相等问题转化为斜率和为0,从而直曲联立,建立韦达定理得到N的坐标.
【详解】解:(1)设切线的方程为,∵与圆相切,
∴,解得或.∴的方程为或;
(2)假设存在,当直线与轴不垂直时,设直线的方程为,代入,得,
设,,∴,.
∵,
而
,
∵,
∴,即,得.
当直线与轴垂直时,也成立.故存在点,使得.
【点睛】本题主要考查直线与圆的位置关系,将角度相等问题转化为斜率和为0问题是解决本题的关键,意在考查学生的计算能力及划归能力.
数学试题
一、选择题,
1.直线 的倾斜角为( )
A. B. C. D.
2.奥林匹克会旗中央有5个互相套连的圆环,颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作,每人分得1个,则事件“甲分得红色”与“乙分得红色”是( )
A. 对立事件 B. 不可能事件
C. 互斥但不对立事件 D. 不是互斥事件
3.对于空间中的直线,以及平面,,下列说法正确的是( )
A. 若,,,则
B. 若,,,则
C. 若 ,,,则
D. 若,,,则
4.一组数据的茎叶图如图所示,则数据落在区间内的概率为( )
A. 0.2 B. 0.4 C. 0.5 D. 0.6
5.已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的平均数和方差分别为 ( )
A. B. C. D.
6.空气质量指数是反映空气质量状况的指数,指数值越小,表明空气质量越好,其对应关系如表:
指数值
0~50
51~100
101~150
151~200
201~300
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
如图是某市10月1日-20日指数变化趋势:
下列叙述错误的是( )
A. 这20天中指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
7.按照程序框图(如图)执行,第4个输出的数是( )
A. 5 B. 6 C. 7 D. 8
8.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹马进行一场比赛、齐王获胜的概率是( )
A. B. C. D.
9.为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
A. 12 B. 9 C. 8 D. 6
10.一个圆经过以下三个点,,,且圆心在轴上,则圆的标准方程为( )
A. B.
C. D.
11.若三条直线,,相交于同一点,则点到原点的距离的最小值为( )
A. B. C. D.
12.在四面体中,是边长为的等边三角形,,,,则四面体的体积为( )
A. B. C. D.
二、填空题(将答案填在答题纸上)
13.已知具有线性相关关系的两个量之间的一组数据如表:
0
1
2
3
4
2.2
4.3
4.5
6.7
且回直线方程是,则的值为____.
14.甲、乙、丙三人射击同一目标,命中目标的概率分别为,,,且彼此射击互不影响,现在三人射击该目标各一次,则目标被击中的概率为____.(用数字作答)
15.过点作圆:的两条切线,切点分别为,,则点到直线的距离为____.
16.已知,,,且,,,,.若在线段上(不含端点)存在不同的两点,使得,则实数的取值范围是___.
三、解答题.
17.从含有两件正品,和一件次品的3件产品中每次任取一件,连续取两次,求取出的两件产品中恰有一件是次品的概率.
(1)每次取出不放回;
(2)每次取出后放回.
18.(1)设直线的方程为.若直线在两坐标轴上的截距相等,求直线的方程;
(2)过直线:上的点作直线,若直线,与轴围成的三角形的面积为2,则直线的方程.
19.某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为)进行统计,按照,,,,的分组作出频率分布直方图,已知得分在,的频数分别为8,2.
(1)求样本容量和频率分布直方图中的的值;
(2)估计本次竞赛学生成绩的中位数;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在内的概率.
20.如图1所示,在等腰梯形,,,垂足为,,.将沿折起到的位置,使平面平面,如图2所示,点为棱的中点.
(1)求证:平面;
(2)求证:平面;
21.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 (单位:千元)对年销售量 (单位:)和年利润(单位:千元)的影响,对近8年的年宣传费和年销售量数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
563
6.8
298.8
1.6
1469
108.8
表中,
(1)根据散点图判断,与哪一个适宜作为年销售量关于年宣传费的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立关于的回归方程;
(3)以知这种产品的年利率与、的关系为.根据(2)的结果求年宣传费时,年销售量及年利润的预报值是多少?
附:对于一组数据,……,其回归线的斜率和截距的最小二乘估计分别为:,
22.已知圆:.
(1)过点向圆引切线,求切线的方程;
(2)过点任作一条直线交圆于、两点,问在轴上是否存在点,使得?若存在,求出的坐标,若不存在,请说明理由.
答案与解析
一、选择题,
1.直线 的倾斜角为( )
A. B. C. D.
【答案】A
【解析】
【分析】
直线的倾斜角就是斜率,从而求得倾斜角.
【详解】解:直线的斜率,设其倾斜角为,,
则,∴.故选:A.
【点睛】本题主要考查直线的倾斜角及斜率的关系,难度较小.
2.奥林匹克会旗中央有5个互相套连的圆环,颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作,每人分得1个,则事件“甲分得红色”与“乙分得红色”是( )
A. 对立事件 B. 不可能事件
C. 互斥但不对立事件 D. 不是互斥事件
【答案】C
【解析】
甲、乙不能同时得到红色,因而这两个事件是互斥事件;又甲、乙可能都得不到红色,即“甲或乙分得红色”的事件不是必然事件,故这两个事件不是对立事件.选C.
3.对于空间中的直线,以及平面,,下列说法正确的是( )
A. 若,,,则
B. 若,,,则
C. 若 ,,,则
D. 若,,,则
【答案】D
【解析】
【分析】
根据空间直线和平面的位置关系对四个选项逐一排除,由此确定正确的选项
【详解】对于A选项,可能异面,故A错误;对于B选项,可能有,故B错误;对于C选项,的夹角不一定为90°,故C错误;因为,故,因为,故,故D正确,故选D.
【点睛】本小题主要考查空间两条直线的位置关系,考查直线和平面、平面和平面位置关系的判断,属于基础题.
4.一组数据的茎叶图如图所示,则数据落在区间内的概率为( )
A. 0.2 B. 0.4 C. 0.5 D. 0.6
【答案】D
【解析】
【分析】
根据茎叶图个原始数据落在区间内的个数,由古典概型的概率公式可得结论.
【详解】由茎叶图个原始数据,数出落在区间内的共有6个,
包括2个个个,2个30,
所以数据落在区间内的概率为,故选D.
【点睛】本题主要考查古典概型概率公式的应用,属于简单题. 在解古典概型概率题时,首先求出样本空间中基本事件的总数,其次求出概率事件中含有多少个基本事件,然后根据公式求得概率.
5.已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的平均数和方差分别为 ( )
A. B. C. D.
【答案】A
【解析】
【分析】
由中位数为5,求出x值,再利用平均数和方差公式计算即可得到答案.
【详解】∵﹣1,0,4,x,7,14中位数为5,
∴,
∴x=6,
∴这组数据的平均数是
这组数据的方差是
故选:A.
【点睛】本题考查对一组数据的中位数,平均数,方差的计算,掌握各公式是求解的关键.
6.空气质量指数是反映空气质量状况的指数,指数值越小,表明空气质量越好,其对应关系如表:
指数值
0~50
51~100
101~150
151~200
201~300
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
如图是某市10月1日-20日指数变化趋势:
下列叙述错误的是( )
A. 这20天中指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
【答案】C
【解析】
【分析】
根据所给图象,结合中位数的定义、指数与污染程度的关系以及古典概型概率公式,对四个选项逐一判断即可.
【详解】对,因为第10天与第11天指数值都略高100,所以中位数略高于100,正确;
对,中度污染及以上的有第11,13,14,15,17天,共5天占,正确;
对,由图知,前半个月中,前4天的空气质量越来越好,后11天该市的空气质量越来越差,错误;
对,由图知,10月上旬大部分指数在100以下,10月中旬大部分指数在100以上,所以正确,故选C.
【点睛】与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际问题转化为数学模型进行解答.
7.按照程序框图(如图)执行,第4个输出的数是( )
A. 5 B. 6 C. 7 D. 8
【答案】C
【解析】
【分析】
按步骤写出对应程序,从而得到答案.
【详解】解:第一次输出的,则,满足条件,然后
第二次输出的,则,满足条件,然后
第三次输出的,则,满足条件,然后
第四次输出的,则,满足条件,然后
第五次输出的,则,不满足条件,然后退出循环
故第4个输出的数是7 故选:C.
【点睛】本题主要考查算法框图,重在考查学生的计算能力和分析能力.
8.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马,现从双方的马匹中随机选一匹马进行一场比赛、齐王获胜的概率是( )
A. B. C. D.
【答案】A
【解析】
【分析】
首先求出满足 “从双方的马匹中随机选一匹马进行一场比赛” 这一条件的事件数,然后求出满足“齐王获胜”这一条件的事件数,根据古典概型公式得出结果.
【详解】解:因为双方各有3匹马,
所以“从双方的马匹中随机选一匹马进行一场比赛”的事件数为9种,
满足“齐王获胜”的这一条件的情况为:
齐王派出上等马,则获胜的事件数为3;
齐王派出中等马,则获胜的事件数为2;
齐王派出下等马,则获胜的事件数为1;
故满足“齐王获胜”这一条件的事件数为6种,
根据古典概型公式可得,齐王获胜的概率,故选A.
【点睛】本题考查了古典概型问题,解题的关键是求出满足条件的事件数,再根据古典概型的计算公式求解问题,属于基础题.
9.为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
A. 12 B. 9 C. 8 D. 6
【答案】B
【解析】
试题分析:根据题意,设阴影部分的面积为S,则正方形的面积为36,
向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,
则向正方形内随机投掷一点,其落到阴影部分概率P=;
而,则,
解可得,S=9;
考点:模拟方法估计概率
10.一个圆经过以下三个点,,,且圆心在轴上,则圆的标准方程为( )
A. B.
C. D.
【答案】D
【解析】
【分析】
根据题意设出圆心,利用圆心到三点的距离相等建立等式,从而求得标准方程.
【详解】解:设圆心坐标为,半径为,则圆的方程为,
则,解得,.
∴圆的标准方程为.
故选:D.
【点睛】本题主要考查圆的标准方程,重点找出圆心及半径是关键,难度不大.
11.若三条直线,,相交于同一点,则点到原点的距离的最小值为( )
A. B. C. D.
【答案】A
【解析】
【分析】
联立直线求得交点,找出m,n的关系,从而表示出距离得到答案.
【详解】解:联立,解得,.
∵三条直线,,相交于同一点,∴.
则点到原点的距离的最小值为原点到直线的距离.
故选:A.
【点睛】本题主要考查学生的计算能力,以及对点线距的掌握情况,难度不大.
12.在四面体中,是边长为的等边三角形,,,,则四面体的体积为( )
A. B. C. D.
【答案】C
【解析】
【分析】
把四面体补成如图所示的三棱锥,其中,可以证明平面且、均为直角三角形,通过计算可得.
【详解】如图,延长至,使得,连接,
因为,故为等腰三角形,
又,故,
所以即,故,
因为,所以,所以,
因,平面,平面,
所以平面,
所以,
因为的中点,所以,
因为,故为直角三角形,
所以,
又,而,故即为直角三角形,
所以,所以,故选C.
【点睛】不规则三棱锥的体积的计算,应尽量找寻其高,如果高难以确定,则可以把给定的几何体补成容易计算体积的几何体,注意补体时利用已有的垂直关系.
二、填空题(将答案填在答题纸上)
13.已知具有线性相关关系的两个量之间的一组数据如表:
0
1
2
3
4
2.2
4.3
4.5
6.7
且回直线方程是,则的值为____.
【答案】4.8
【解析】
【分析】
求出数据中心,代入回归方程即可求出m的值.
【详解】2,.
∴0.95×2+2.6,解得m=4.8.
故答案为4.8.
【点睛】本题考查了线性回归方程的性质,属于基础题.
14.甲、乙、丙三人射击同一目标,命中目标的概率分别为,,,且彼此射击互不影响,现在三人射击该目标各一次,则目标被击中的概率为____.(用数字作答)
【答案】
【解析】
分析:根据独立事件同时发生的概率和对立事件的概率公式求解即可.
详解:由题意得,甲、乙、丙三人射击同一目标都未击中的概率为
,
所以甲、乙、丙至少一人击中的概率为,
即目标被击中的概率为.
点睛:解答概率问题的关键是认清概率的类型、选择合适的公式求解,对于含有“至多”、“至少”等词语的问题一般可根据对立事件的概率求解,可减少运算量、提高解题的效率.
15.过点作圆:的两条切线,切点分别为,,则点到直线的距离为____.
【答案】
【解析】
【分析】
根据圆的切线长定理,可知 ,设则的长度就是点到直线的距离,在中,利用相似三角形,得到比例式,可以求出,进而求出。
【详解】连接 设因为是圆的两条切线,所以
则,显然相似于
所以点到直线的距离为。
【点睛】本题考查了直线与圆的位置关系,解题中充分利用直角三角形相似是关键。
16.已知,,,且,,,,.若在线段上(不含端点)存在不同的两点,使得,则实数的取值范围是___.
【答案】
【解析】
【分析】
利用距离关系即可列出不等式,从而得到取值范围.
【详解】解:直线方程,即,由已知得且则可得到,由于,所以,则,由于则,所以,所以
解得:
【点睛】本题主要考查直线与圆位置关系的关系,利用点线距建立不等式是解题的关键,难度中档.
三、解答题.
17.从含有两件正品,和一件次品的3件产品中每次任取一件,连续取两次,求取出的两件产品中恰有一件是次品的概率.
(1)每次取出不放回;
(2)每次取出后放回.
【答案】(1)
(2)
【解析】
试题分析:
(1)由题意列出所有可能的结果,共有6种,然后结合古典概型公式可得每次取出不放回的概率为;
(2) 由题意列出所有可能的结果,共有9种,然后结合古典概型公式可得每次取出放回的概率为;
试题解析:
(1)每次取出一个,取后不放回地连续取两次,其一切可能的结果组成的基本事件有6个,即.用A表示“取出的两件中,恰好有一件次品”这一事件,则.
(2)由题意知本题是一个古典概型,试验发生包含的事件是每次取出一个,取后放回地连续取两次,其一切可能的结果组成的基本事件有9个,即:
用B表示“取出的两种中,恰好有一件次品”这一事件,则.
18.(1)设直线的方程为.若直线在两坐标轴上的截距相等,求直线的方程;
(2)过直线:上的点作直线,若直线,与轴围成的三角形的面积为2,则直线的方程.
【答案】(1) 或 (2) 或.
【解析】
【分析】
(1)表示出截距,然后建立等量关系得到答案.
(2)计算出与x,y轴的坐标,然后建立等量关系,即可得到直线方程.
【详解】解:(1)当直线过原点时,该直线在轴和轴上的截距为0,∴,方程即为.
当直线不经过原点时,截距存在且均不为0,直线方程为 ∴
∴,方程即为.综上,直线的方程为或.
(2)①若直线的斜率不存在,则直线的方程为,
直线,直线和轴围成的三角形的面积为2,符合题意;
②若直线的斜率,则直线与轴没有交点,不符合题意;
③若直线的斜率,设其方程为,令,得,依题意
有,解得,所以直线的方程为,即.
综上可知,直线的方程为或.
【点睛】本题主要考查直线的相关量的含义,截距不是距离,注意截距为0的情况。细心分析题目,难度不大.
19.某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为)进行统计,按照,,,,的分组作出频率分布直方图,已知得分在,的频数分别为8,2.
(1)求样本容量和频率分布直方图中的的值;
(2)估计本次竞赛学生成绩的中位数;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在内的概率.
【答案】(1);(2);(3).
【解析】
试题分析:(1)借助题设条件运用频率分布直方图求解;(2)借助题设条件运用频率分布直方图中提供的数据信息求解;(3)运用列举法和古典概型计算公式求解.
试题解析:
(1)由题意可知,样本容量n==50, ……………………2分
,x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030; ……………………4分
(2)设本次竞赛学生成绩的中位数为m,平均分为,
则[0.016+0.03]×10+(m﹣70)×0.040 =0.5,解得, ……………………6分
=(55×0.016+65×0.030+75×0.040+85×0.010+95×0.004]×10=70.6, ……………………8分
(3)由题意可知,分数在[80,90)内的学生有5人,记这5人分别为a1,a2,a3,a4,a5,
分数在[90,100]内的学生有2人,记这2人分别为b1,b2.抽取的2名学生的所有情况有21种,
分别为:(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a1,b1),(a1,b2),(a2,a3),
(a2,a4),(a2,a5),(a2,b1),(a2,b2),(a3,a4),(a3,a5),(a3,b1),
(a3,b2),(a4,a5),(a4,b1),(a4,b2),(a5,b1),(a5,b2),(b1,b2). ……………………10分
其中2名同学的分数都不在[90,100]内的情况有10种,分别为:
(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a2,a3),(a2,a4),(a2,a5),(a3,a4),(a3,a5),(a4,a5).
∴所抽取的2名学生中至少有一人得分在[90,100]内的概率. ……………………12分
考点:频率分布直方图、频率与频数的关系及古典概型的计算公式等有关知识的综合运用.
【易错点晴】本题以学校中数学竞赛的数学成绩的抽样统计的频率分布直方图为背景,设置了三个较为平常的数学问题.解答时一定要充分利用题设中提供的频率分布直方图所提供的数据信息,结合题设条件进行求解.第一问中求的是频率分布直方图中的未知数的值,运用该频率分布直方图时一定要注意该图的纵坐标是频率与组距的比值,这一点解题很容易被忽视.第二问中求的是中位数和平均数,求解时先依据中位数这个概念建立了方程求解,再运用平均数公式进行求解;第三问是运用简单枚举法一一列举出基本事件的所有可能和符合条件的事件的可能,最后运用古典概型的计算公式求出其概率的值.这是一道非常平常的考查基础知识和基本方法的基础题.
20.如图1所示,在等腰梯形,,,垂足为,,.将沿折起到的位置,使平面平面,如图2所示,点为棱的中点.
(1)求证:平面;
(2)求证:平面;
【答案】(1)见证明;(2)见证明
【解析】
【分析】
(1)利用线线平行可证明线面平行;
(2)利用线线垂直可证明线面垂直.
【详解】(1)证明:在图1的等腰梯形内,过作的垂线,垂足为,
∵,∴,又∵,,,
∴四边形为正方形,且,为中点.
在图2中,连结,∵点是的中点,∴.
又∵,,,平面,,平面,
∴平面平面,又∵面,∴平面;
(2)证明:∵平面平面,平面平面,,
平面,∴平面.又∵平面,∴.
又,,,满足,
∴.又,
平面;
【点睛】注意线面垂直和线面平面的判定方法,意在考查学生的理解能力和空间想象能力,难度中档.
21.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 (单位:千元)对年销售量 (单位:)和年利润(单位:千元)的影响,对近8年的年宣传费和年销售量数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
563
6.8
298.8
1.6
1469
108.8
表中,
(1)根据散点图判断,与哪一个适宜作为年销售量关于年宣传费的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立关于的回归方程;
(3)以知这种产品的年利率与、的关系为.根据(2)的结果求年宣传费时,年销售量及年利润的预报值是多少?
附:对于一组数据,……,其回归线的斜率和截距的最小二乘估计分别为:,
【答案】(1) 适宜作为年销售量关于年宣传费的回归方程类型. (2) (3)66.32
【解析】
【分析】
(1)根据图形可知选择曲线更加符合;
(2)通过最小二乘法计算即可得到回归方程;
(3)找到z和x的函数,转化为二次函数即可得到最值.
【详解】解:(1)由散点图可以判断,适宜作为年销售量关于年宣传费的回归方程类型.
(2)令,先建立关于的线性回归方程.由于
,.
所以关于线性回归方程为,
因此关于的回归方程为.
(3)(i)由(II)知,当时,年销售量的预报值
年利润的预报值.
【点睛】本题主要考查回归分析,对相关含义的理解是解决本题的关键,意在考查学生的转化能力及计算能力.
22.已知圆:.
(1)过点向圆引切线,求切线的方程;
(2)过点任作一条直线交圆于、两点,问在轴上是否存在点,使得?若存在,求出的坐标,若不存在,请说明理由.
【答案】(1) 或;(2)见解析
【解析】
【分析】
(1)通过直线与圆的位置关系相切,建立方程计算得到直线方程;
(2)将角度相等问题转化为斜率和为0,从而直曲联立,建立韦达定理得到N的坐标.
【详解】解:(1)设切线的方程为,∵与圆相切,
∴,解得或.∴的方程为或;
(2)假设存在,当直线与轴不垂直时,设直线的方程为,代入,得,
设,,∴,.
∵,
而
,
∵,
∴,即,得.
当直线与轴垂直时,也成立.故存在点,使得.
【点睛】本题主要考查直线与圆的位置关系,将角度相等问题转化为斜率和为0问题是解决本题的关键,意在考查学生的计算能力及划归能力.
同课章节目录
