人教版数学四年级下册第九单元《数学广角——鸡兔同笼》教案(表格版)
文档属性
| 名称 | 人教版数学四年级下册第九单元《数学广角——鸡兔同笼》教案(表格版) |
|
|
| 格式 | zip | ||
| 文件大小 | 22.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-03 00:00:00 | ||
图片预览

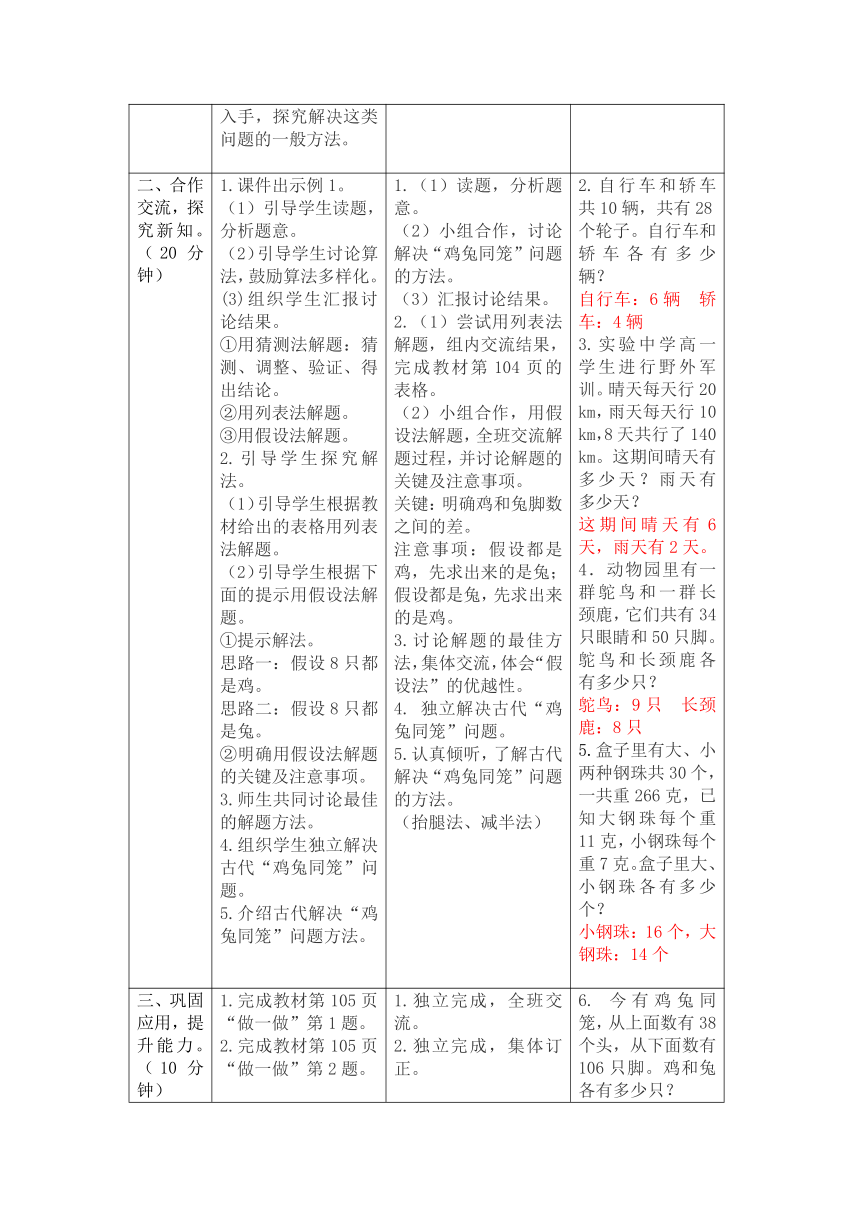
文档简介
数学广角——鸡兔同笼
教学设计表
学科:数学 年级:四年级 册次:下 学校: 教师:
课题
数学广角——鸡兔同笼(P103、P104例1)
课型
新授课
计划学时
1
教学内容分析
例1是在古代趣题的基础上呈现的一道数据较小的“鸡兔同笼”问题。在引导学生探索解题方法的过程中,呈现了猜测、列表、假设等方法。
承前启后
分析应用题的方法→“鸡兔同笼”问题的解法→解决问题的策略
教学目标
1.了解“鸡兔同笼”问题的结构特点,掌握用“假设法”“猜测法”“列表法”解决问题的具体过程,初步形成解决此类问题的一般性策略。
2.经历用不同的方法解决“鸡兔同笼”问题的过程,使学生体会解题策略的多样化,渗透化繁为简的思想。
重难点
重点:尝试用不同的方法解决“鸡兔同笼”问题,体会用“假设法”解决问题的优越性。
难点:理解用“假设法”解决“鸡兔同笼”问题的算理。
化解措施
猜测验证,合作探究。
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教具准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.课件出示教材第103页主题图。
(1)组织学生说一说获得了哪些信息。
(2)出示“鸡兔同笼”原题,简介来历。
(3)让学生通过猜测、估计,并进行数据调整,尝试解决问题。
2.导入新课:因为“鸡兔同笼”问题比较难解,所以本节课我们采用“化繁为简”的方法,从简单的问题入手,探究解决这类问题的一般方法。
1.(1)交流,并汇报获取的信息。
(2)理解“鸡兔同笼”原题的题意。
(3)先估计、猜测鸡兔各有多少只,再调整数据,发现由于原题数据比较大,不容易得出答案,体会从简单问题入手的必要性。
?2.明确本节课的学习内容。
1.填空。
大约一千五百年前,我国古代数学名著(《孙子算经》)中记载了一道数学趣题,就是著名的“鸡兔同笼”问题?。
二、合作交流,探究新知。(20分钟)
1.课件出示例1。
(1)引导学生读题,分析题意。
(2)引导学生讨论算法,鼓励算法多样化。
(3)组织学生汇报讨论结果。
①用猜测法解题:猜测、调整、验证、得出结论。
②用列表法解题。
③用假设法解题。
2.引导学生探究解法。
(1)引导学生根据教材给出的表格用列表法解题。
(2)引导学生根据下面的提示用假设法解题。
①提示解法。
思路一:假设8只都是鸡。
思路二:假设8只都是兔。
②明确用假设法解题的关键及注意事项。
3.师生共同讨论最佳的解题方法。
4.组织学生独立解决古代“鸡兔同笼”问题。
5.介绍古代解决“鸡兔同笼”问题方法。
1.(1)读题,分析题意。
(2)小组合作,讨论解决“鸡兔同笼”问题的方法。
(3)汇报讨论结果。
2.(1)尝试用列表法解题,组内交流结果,完成教材第104页的表格。
(2)小组合作,用假设法解题,全班交流解题过程,并讨论解题的关键及注意事项。
关键:明确鸡和兔脚数之间的差。
注意事项:假设都是鸡,先求出来的是兔;假设都是兔,先求出来的是鸡。
3.讨论解题的最佳方法,集体交流,体会“假设法”的优越性。
4. 独立解决古代“鸡兔同笼”问题。
5.认真倾听,了解古代解决“鸡兔同笼”问题的方法。
(抬腿法、减半法)
2.自行车和轿车共10辆,共有28个轮子。自行车和轿车各有多少辆?
自行车:6辆 轿车:4辆
3.实验中学高一学生进行野外军训。晴天每天行20 km,雨天每天行10 km,8天共行了140 km。这期间晴天有多少天?雨天有多少天?
这期间晴天有6天,雨天有2天。
4.动物园里有一群鸵鸟和一群长颈鹿,它们共有34只眼睛和50只脚。鸵鸟和长颈鹿各有多少只?
鸵鸟:9只 长颈鹿:8只
5.盒子里有大、小两种钢珠共30个,一共重266克,已知大钢珠每个重11克,小钢珠每个重7克。盒子里大、小钢珠各有多少个?
小钢珠:16个,大钢珠:14个
三、巩固应用,提升能力。(10分钟)
1.完成教材第105页“做一做”第1题。
2.完成教材第105页“做一做”第2题。
1.独立完成,全班交流。
2.独立完成,集体订正。
6. 今有鸡兔同笼,从上面数有38个头,从下面数有106只脚。鸡和兔各有多少只?
鸡:23只 兔:15只
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.用假设法解“鸡兔同笼”问题有多种思路,古人用的抬腿法就是假设法的另一种情况。
教师个人补充意见:
板书设计
数学广角——鸡兔同笼
培优作业
1.鸡与兔共有120只,鸡比兔多120只脚。鸡和兔各有多少只?
兔的只数:
(2×120-120)÷(2+4)
=120÷6
=20(只)
鸡的只数:120-20=100(只)
2.100个和尚共吃100个馒头,大和尚每人吃3个,小和尚每3个人吃1个,求大、小和尚各有多少人。
100个和尚可以分为100÷4=25(组),因为每个组里有1个大和尚和3个小和尚,所以大和尚的人数是1×25=25(人),小和尚的人数是100-25=75(人)。
3.小红参加数学竞赛,共20道题,规定答对一题得5分,答错一题倒扣3分(不答按答错计算),小红做完这些题共得68分。小红答对了多少道题,答错了多少道题?
答错的题数:(20×5-68)÷(5+3)=4(道)
答对的题数:20-4=16(道)
答:小红答对了16道题,答错了4道题。
4.蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀(蝉另一对较小的翅膀忽略不计)。现有三种动物18只,共112条腿和22对翅膀,蜘蛛、蜻蜓、蝉各有几只?
蜘蛛:(112-6×18)÷(8-6)=2(只)
蜻蜓和蝉的只数之和:18-2=16(只)
蜻蜓:(22-16×1)÷(2-1)=6(只)
蝉:16-6=10(只)
答:蜘蛛有2只,蜻蜓有6只,蝉有10只。
提示:因为蜻蜓和蝉都有6条腿,所以可以把蜻蜓和蝉看作一组,蜘蛛看作另一组,先根据腿数求出蜘蛛的只数以及蜻蜓和蝉的只数之和,再根据翅膀的对数分别求出蜻蜓和蝉的只数。
教学反思
“鸡兔同笼”问题的解题方法有很多,教学中教师要适时引导和点拨,鼓励学生尝试多种解法,同时使学生正确地理解每一种解法。
微课设计点
教师可围绕“解决鸡兔同笼问题的方法”设计微课。
教学设计表
学科:数学 年级:四年级 册次:下 学校: 教师:
课题
数学广角——鸡兔同笼(P103、P104例1)
课型
新授课
计划学时
1
教学内容分析
例1是在古代趣题的基础上呈现的一道数据较小的“鸡兔同笼”问题。在引导学生探索解题方法的过程中,呈现了猜测、列表、假设等方法。
承前启后
分析应用题的方法→“鸡兔同笼”问题的解法→解决问题的策略
教学目标
1.了解“鸡兔同笼”问题的结构特点,掌握用“假设法”“猜测法”“列表法”解决问题的具体过程,初步形成解决此类问题的一般性策略。
2.经历用不同的方法解决“鸡兔同笼”问题的过程,使学生体会解题策略的多样化,渗透化繁为简的思想。
重难点
重点:尝试用不同的方法解决“鸡兔同笼”问题,体会用“假设法”解决问题的优越性。
难点:理解用“假设法”解决“鸡兔同笼”问题的算理。
化解措施
猜测验证,合作探究。
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教具准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.课件出示教材第103页主题图。
(1)组织学生说一说获得了哪些信息。
(2)出示“鸡兔同笼”原题,简介来历。
(3)让学生通过猜测、估计,并进行数据调整,尝试解决问题。
2.导入新课:因为“鸡兔同笼”问题比较难解,所以本节课我们采用“化繁为简”的方法,从简单的问题入手,探究解决这类问题的一般方法。
1.(1)交流,并汇报获取的信息。
(2)理解“鸡兔同笼”原题的题意。
(3)先估计、猜测鸡兔各有多少只,再调整数据,发现由于原题数据比较大,不容易得出答案,体会从简单问题入手的必要性。
?2.明确本节课的学习内容。
1.填空。
大约一千五百年前,我国古代数学名著(《孙子算经》)中记载了一道数学趣题,就是著名的“鸡兔同笼”问题?。
二、合作交流,探究新知。(20分钟)
1.课件出示例1。
(1)引导学生读题,分析题意。
(2)引导学生讨论算法,鼓励算法多样化。
(3)组织学生汇报讨论结果。
①用猜测法解题:猜测、调整、验证、得出结论。
②用列表法解题。
③用假设法解题。
2.引导学生探究解法。
(1)引导学生根据教材给出的表格用列表法解题。
(2)引导学生根据下面的提示用假设法解题。
①提示解法。
思路一:假设8只都是鸡。
思路二:假设8只都是兔。
②明确用假设法解题的关键及注意事项。
3.师生共同讨论最佳的解题方法。
4.组织学生独立解决古代“鸡兔同笼”问题。
5.介绍古代解决“鸡兔同笼”问题方法。
1.(1)读题,分析题意。
(2)小组合作,讨论解决“鸡兔同笼”问题的方法。
(3)汇报讨论结果。
2.(1)尝试用列表法解题,组内交流结果,完成教材第104页的表格。
(2)小组合作,用假设法解题,全班交流解题过程,并讨论解题的关键及注意事项。
关键:明确鸡和兔脚数之间的差。
注意事项:假设都是鸡,先求出来的是兔;假设都是兔,先求出来的是鸡。
3.讨论解题的最佳方法,集体交流,体会“假设法”的优越性。
4. 独立解决古代“鸡兔同笼”问题。
5.认真倾听,了解古代解决“鸡兔同笼”问题的方法。
(抬腿法、减半法)
2.自行车和轿车共10辆,共有28个轮子。自行车和轿车各有多少辆?
自行车:6辆 轿车:4辆
3.实验中学高一学生进行野外军训。晴天每天行20 km,雨天每天行10 km,8天共行了140 km。这期间晴天有多少天?雨天有多少天?
这期间晴天有6天,雨天有2天。
4.动物园里有一群鸵鸟和一群长颈鹿,它们共有34只眼睛和50只脚。鸵鸟和长颈鹿各有多少只?
鸵鸟:9只 长颈鹿:8只
5.盒子里有大、小两种钢珠共30个,一共重266克,已知大钢珠每个重11克,小钢珠每个重7克。盒子里大、小钢珠各有多少个?
小钢珠:16个,大钢珠:14个
三、巩固应用,提升能力。(10分钟)
1.完成教材第105页“做一做”第1题。
2.完成教材第105页“做一做”第2题。
1.独立完成,全班交流。
2.独立完成,集体订正。
6. 今有鸡兔同笼,从上面数有38个头,从下面数有106只脚。鸡和兔各有多少只?
鸡:23只 兔:15只
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.用假设法解“鸡兔同笼”问题有多种思路,古人用的抬腿法就是假设法的另一种情况。
教师个人补充意见:
板书设计
数学广角——鸡兔同笼
培优作业
1.鸡与兔共有120只,鸡比兔多120只脚。鸡和兔各有多少只?
兔的只数:
(2×120-120)÷(2+4)
=120÷6
=20(只)
鸡的只数:120-20=100(只)
2.100个和尚共吃100个馒头,大和尚每人吃3个,小和尚每3个人吃1个,求大、小和尚各有多少人。
100个和尚可以分为100÷4=25(组),因为每个组里有1个大和尚和3个小和尚,所以大和尚的人数是1×25=25(人),小和尚的人数是100-25=75(人)。
3.小红参加数学竞赛,共20道题,规定答对一题得5分,答错一题倒扣3分(不答按答错计算),小红做完这些题共得68分。小红答对了多少道题,答错了多少道题?
答错的题数:(20×5-68)÷(5+3)=4(道)
答对的题数:20-4=16(道)
答:小红答对了16道题,答错了4道题。
4.蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀(蝉另一对较小的翅膀忽略不计)。现有三种动物18只,共112条腿和22对翅膀,蜘蛛、蜻蜓、蝉各有几只?
蜘蛛:(112-6×18)÷(8-6)=2(只)
蜻蜓和蝉的只数之和:18-2=16(只)
蜻蜓:(22-16×1)÷(2-1)=6(只)
蝉:16-6=10(只)
答:蜘蛛有2只,蜻蜓有6只,蝉有10只。
提示:因为蜻蜓和蝉都有6条腿,所以可以把蜻蜓和蝉看作一组,蜘蛛看作另一组,先根据腿数求出蜘蛛的只数以及蜻蜓和蝉的只数之和,再根据翅膀的对数分别求出蜻蜓和蝉的只数。
教学反思
“鸡兔同笼”问题的解题方法有很多,教学中教师要适时引导和点拨,鼓励学生尝试多种解法,同时使学生正确地理解每一种解法。
微课设计点
教师可围绕“解决鸡兔同笼问题的方法”设计微课。
