人教版数学四年级下册10.2《图形与几何》教案(表格版)
文档属性
| 名称 | 人教版数学四年级下册10.2《图形与几何》教案(表格版) |
|
|
| 格式 | zip | ||
| 文件大小 | 74.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-03 00:00:00 | ||
图片预览


文档简介
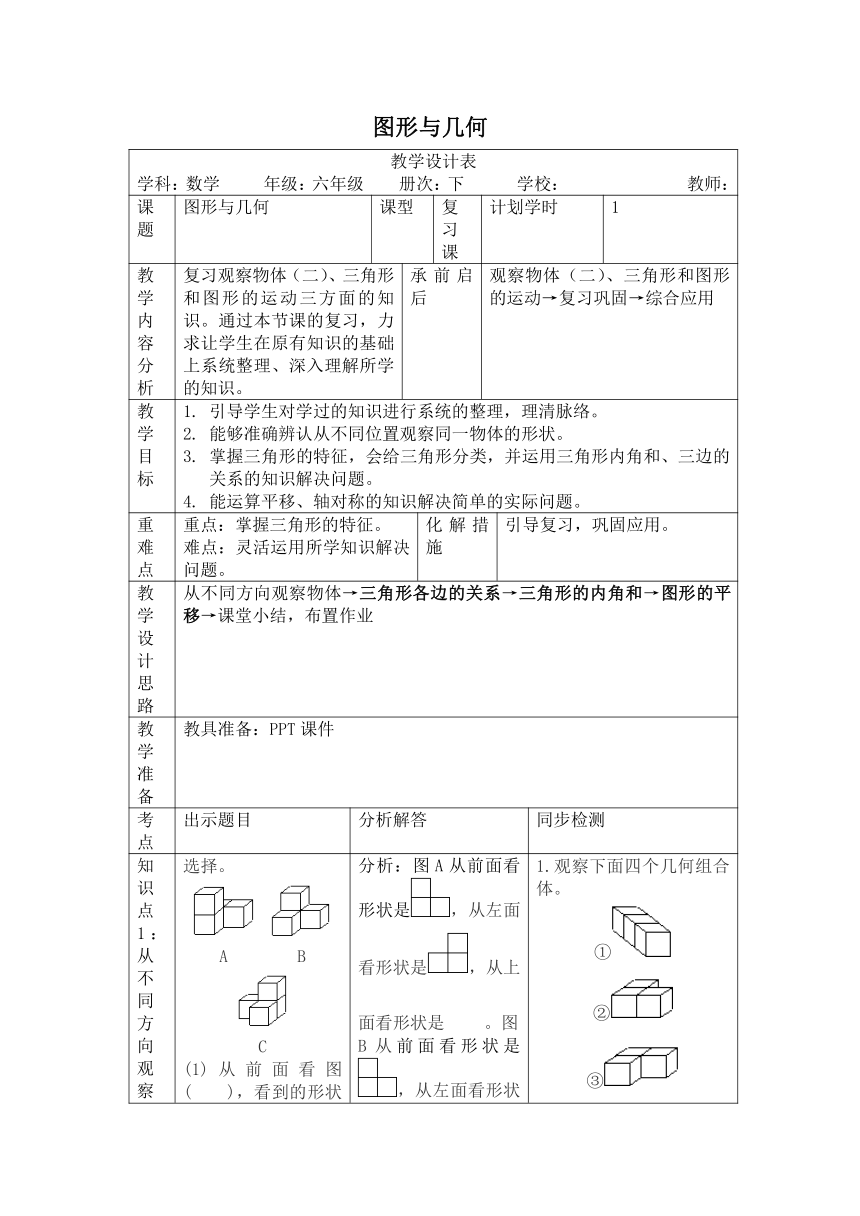
图形与几何
教学设计表
学科:数学 年级:六年级 册次:下 学校: 教师:
课题
图形与几何
课型
复习课
计划学时
1
教学内容分析
复习观察物体(二)、三角形和图形的运动三方面的知识。通过本节课的复习,力求让学生在原有知识的基础上系统整理、深入理解所学的知识。
承前启后
观察物体(二)、三角形和图形的运动→复习巩固→综合应用
教学目标
引导学生对学过的知识进行系统的整理,理清脉络。
能够准确辨认从不同位置观察同一物体的形状。
掌握三角形的特征,会给三角形分类,并运用三角形内角和、三边的关系的知识解决问题。
能运算平移、轴对称的知识解决简单的实际问题。
重难点
重点:掌握三角形的特征。
难点:灵活运用所学知识解决问题。
化解措施
引导复习,巩固应用。
教学设计思路
从不同方向观察物体→三角形各边的关系→三角形的内角和→图形的平移→课堂小结,布置作业
教学准备
教具准备:PPT课件
考点
出示题目
分析解答
同步检测
知识点1:从不同方向观察物体。
选择。
/ /
A B
/ C
(1)从前面看图( ),看到的形状是?/。
(2)从前面和左面看图( ),看到的形状都是?/。
(3)从左面看图( ),看到的形状是?/。
(4)从上面看图( ),看到的形状是?/。
分析:图A从前面看形状是/,从左面看形状是/,从上面看形状是/。图B从前面看形状是/,从左面看形状是/,从上面看形状是/。图C从前面看形状是/,从左面看形状是/,从上面看形状是/。
规范解答:(1)A、B (2) B (3)B、C (4)A、B
1.观察下面四个几何组合体。
①/
②/
③/
④/
(1)从前面看,哪几个几何组合体的形状是相同的?
②③④
(2)从右面看,哪几个几何组合体的形状是相同的?
②③④
知识点2:三角形各边的关系。
在能围成三角形的数据后面画“√”。
(1)2厘米、3厘米、4厘米 ( )
(2)10厘米、17厘米、30厘米 ( )
(3)4分米、4分米、1米 ( )
(4)7米、8米、12米 ( )
分析:本题利用“三角形任意两边长度的和大于第三边”来进行判断。第(1)题中2+3>4,2+4>3,3+4>2,这一组数据能围成三角形。同理,第(4)题中的三个数据也可以围成三角形。第(2)题中10+17<30,这组数据不能围成三角形。第(3)题中,1米=10分米,4+4<10,这组数据不能围成三角形。
规范解答:(1)(√)
(2)( )
(3)( )
(4)(√)
2.从下面四条线段中选择三条围成一个三角形,围成的是(等腰)三角形,它的周长是(14)cm。
/
/
/
/
知识点3:三角形的内角和。
如下图,四边形ABCD中,∠D=50°,DA=DC,∠1=20°,AB=AC,求四边形各角的度数。
/
分析:在三角形ACD中,因为DA=DC,所以三角形ACD是等腰三角形,∠D=50°,根据三角形内角和是180°,可求出∠2、∠4的度数,同理可求出∠3的度数。知道∠1、∠2、∠3、∠4的度数,四边形各个内角的度数便可求出。
规范解答:∠2=∠4=(180°-50°)÷2=65°,∠3=∠B=(180°-20°)÷2=80°。
四边形各角的度数:∠D=50°,∠BAD=∠1+∠4=20°+65°=85°,∠B=80°,∠BCD=∠2+∠3=65°+80°=145°。
3.求未知角的度数。
(1)//
∠C=(50°)
(2)
∠1=(20°)
∠2=(145°)
知识点4:图形的平移。
在下面的方格图中,图形A如何平移得到图形B?先回答,再画一画。
/
分析:在平移时,先确定方向,再确定平移的距离。要知道一个图形平移了几格,先找出平移前后相对应的一组点,再数出对应点之间有几格,整个图形就平移了几格。
规范解答:将图形A先向左平移7格,再向下平移3格得到图形B,或将图形A先向下平移3格,再向左平移7格得到图形B。
/
按要求画一画。
/
(1)画出图形A向右平移8格得到的图形B。
(2)画出图形B向下平移4格得到的图形C。
(3)以直线l为对称轴画出图形A的轴对称图形D。
自己完成
课堂小结,布置作业。
1.这节课我们学习了什么?引导学生回顾总结。/
2. 教师布置作业。
教师个人补充意见:
板书设计
图形与几何
观察物体
平移和轴对称
培优作业
如下图,将这个正方体的表面涂上红色。
/
(1)1个面是红色的小正方体有多少个?
24个
(2)2个面是红色的小正方体有多少个?
24个
(3)3个面是红色的小正方体有多少个?
8个
名师点睛
在教学中,结合相应的练习题,对所学知识进行回顾与整理,在完成练习的同时请学生说说相关的概念和理论知识,而不是单纯地让学生背条条框框。这样既能使学生理解所学知识,又能提高学生解决问题的能力。
教学设计表
学科:数学 年级:六年级 册次:下 学校: 教师:
课题
图形与几何
课型
复习课
计划学时
1
教学内容分析
复习观察物体(二)、三角形和图形的运动三方面的知识。通过本节课的复习,力求让学生在原有知识的基础上系统整理、深入理解所学的知识。
承前启后
观察物体(二)、三角形和图形的运动→复习巩固→综合应用
教学目标
引导学生对学过的知识进行系统的整理,理清脉络。
能够准确辨认从不同位置观察同一物体的形状。
掌握三角形的特征,会给三角形分类,并运用三角形内角和、三边的关系的知识解决问题。
能运算平移、轴对称的知识解决简单的实际问题。
重难点
重点:掌握三角形的特征。
难点:灵活运用所学知识解决问题。
化解措施
引导复习,巩固应用。
教学设计思路
从不同方向观察物体→三角形各边的关系→三角形的内角和→图形的平移→课堂小结,布置作业
教学准备
教具准备:PPT课件
考点
出示题目
分析解答
同步检测
知识点1:从不同方向观察物体。
选择。
/ /
A B
/ C
(1)从前面看图( ),看到的形状是?/。
(2)从前面和左面看图( ),看到的形状都是?/。
(3)从左面看图( ),看到的形状是?/。
(4)从上面看图( ),看到的形状是?/。
分析:图A从前面看形状是/,从左面看形状是/,从上面看形状是/。图B从前面看形状是/,从左面看形状是/,从上面看形状是/。图C从前面看形状是/,从左面看形状是/,从上面看形状是/。
规范解答:(1)A、B (2) B (3)B、C (4)A、B
1.观察下面四个几何组合体。
①/
②/
③/
④/
(1)从前面看,哪几个几何组合体的形状是相同的?
②③④
(2)从右面看,哪几个几何组合体的形状是相同的?
②③④
知识点2:三角形各边的关系。
在能围成三角形的数据后面画“√”。
(1)2厘米、3厘米、4厘米 ( )
(2)10厘米、17厘米、30厘米 ( )
(3)4分米、4分米、1米 ( )
(4)7米、8米、12米 ( )
分析:本题利用“三角形任意两边长度的和大于第三边”来进行判断。第(1)题中2+3>4,2+4>3,3+4>2,这一组数据能围成三角形。同理,第(4)题中的三个数据也可以围成三角形。第(2)题中10+17<30,这组数据不能围成三角形。第(3)题中,1米=10分米,4+4<10,这组数据不能围成三角形。
规范解答:(1)(√)
(2)( )
(3)( )
(4)(√)
2.从下面四条线段中选择三条围成一个三角形,围成的是(等腰)三角形,它的周长是(14)cm。
/
/
/
/
知识点3:三角形的内角和。
如下图,四边形ABCD中,∠D=50°,DA=DC,∠1=20°,AB=AC,求四边形各角的度数。
/
分析:在三角形ACD中,因为DA=DC,所以三角形ACD是等腰三角形,∠D=50°,根据三角形内角和是180°,可求出∠2、∠4的度数,同理可求出∠3的度数。知道∠1、∠2、∠3、∠4的度数,四边形各个内角的度数便可求出。
规范解答:∠2=∠4=(180°-50°)÷2=65°,∠3=∠B=(180°-20°)÷2=80°。
四边形各角的度数:∠D=50°,∠BAD=∠1+∠4=20°+65°=85°,∠B=80°,∠BCD=∠2+∠3=65°+80°=145°。
3.求未知角的度数。
(1)//
∠C=(50°)
(2)
∠1=(20°)
∠2=(145°)
知识点4:图形的平移。
在下面的方格图中,图形A如何平移得到图形B?先回答,再画一画。
/
分析:在平移时,先确定方向,再确定平移的距离。要知道一个图形平移了几格,先找出平移前后相对应的一组点,再数出对应点之间有几格,整个图形就平移了几格。
规范解答:将图形A先向左平移7格,再向下平移3格得到图形B,或将图形A先向下平移3格,再向左平移7格得到图形B。
/
按要求画一画。
/
(1)画出图形A向右平移8格得到的图形B。
(2)画出图形B向下平移4格得到的图形C。
(3)以直线l为对称轴画出图形A的轴对称图形D。
自己完成
课堂小结,布置作业。
1.这节课我们学习了什么?引导学生回顾总结。/
2. 教师布置作业。
教师个人补充意见:
板书设计
图形与几何
观察物体
平移和轴对称
培优作业
如下图,将这个正方体的表面涂上红色。
/
(1)1个面是红色的小正方体有多少个?
24个
(2)2个面是红色的小正方体有多少个?
24个
(3)3个面是红色的小正方体有多少个?
8个
名师点睛
在教学中,结合相应的练习题,对所学知识进行回顾与整理,在完成练习的同时请学生说说相关的概念和理论知识,而不是单纯地让学生背条条框框。这样既能使学生理解所学知识,又能提高学生解决问题的能力。
