五年级上册数学课件-9.2图形密铺的奥秘 冀教版(共21张PPT)
文档属性
| 名称 | 五年级上册数学课件-9.2图形密铺的奥秘 冀教版(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-05 09:39:53 | ||
图片预览





文档简介
课件21张PPT。没 有 缝 隙不重叠冀教版五年级上册数学探 索 乐 园
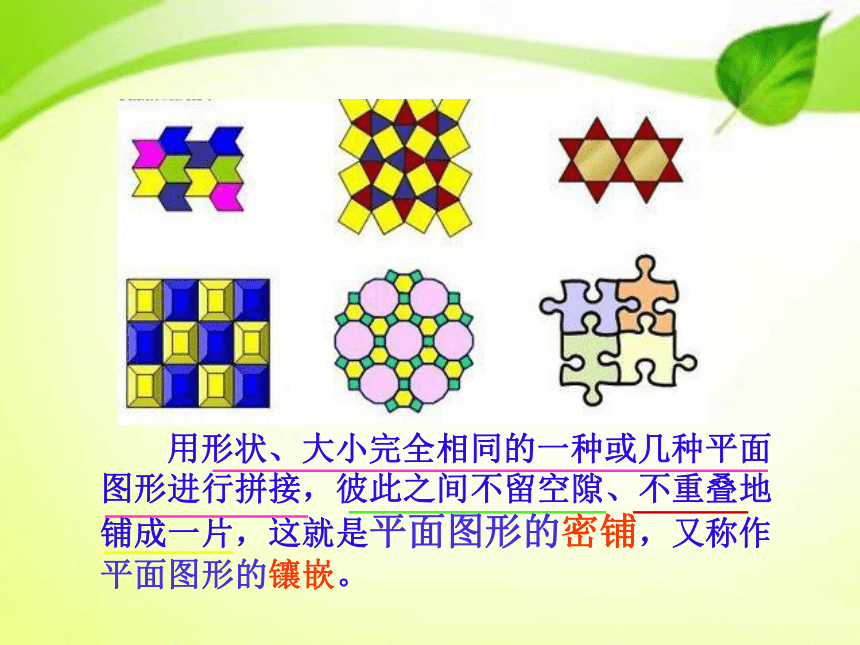
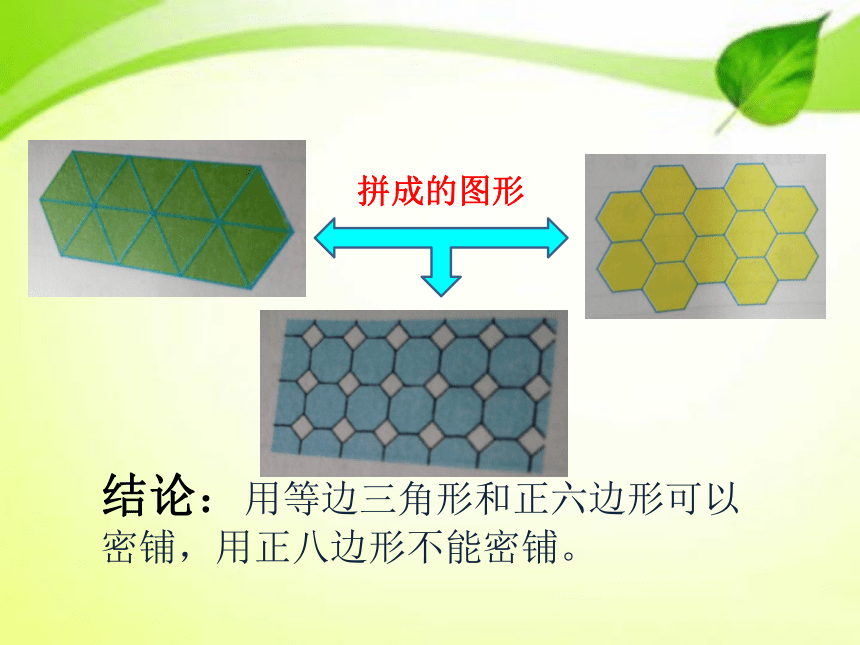
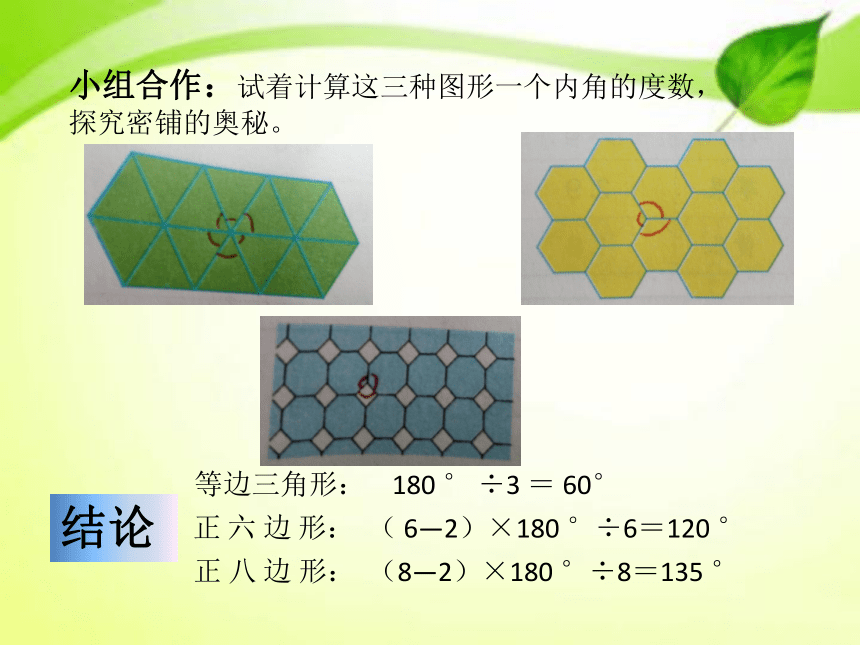
——密铺 无论是什么形状的地砖,只要可以将一块地面的中间既不留空隙,也不重叠铺满,就是密铺。观察图片,试着总结什么叫密铺? 用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称作平面图形的镶嵌。猜一猜:用下面的图形可以密铺吗?怎样知道大家的猜测是否正确呢?咱们来试一试吧!正三角形正六边形正八边形结论:用等边三角形和正六边形可以密铺,用正八边形不能密铺。拼成的图形小组合作:试着计算这三种图形一个内角的度数,探究密铺的奥秘。等边三角形: 180 ° ÷3 = 60° 正 六 边 形: ( 6—2)×180 °÷6=120 °正 八 边 形: (8—2)×180 °÷8=135 °结论能密铺图形的关键是:
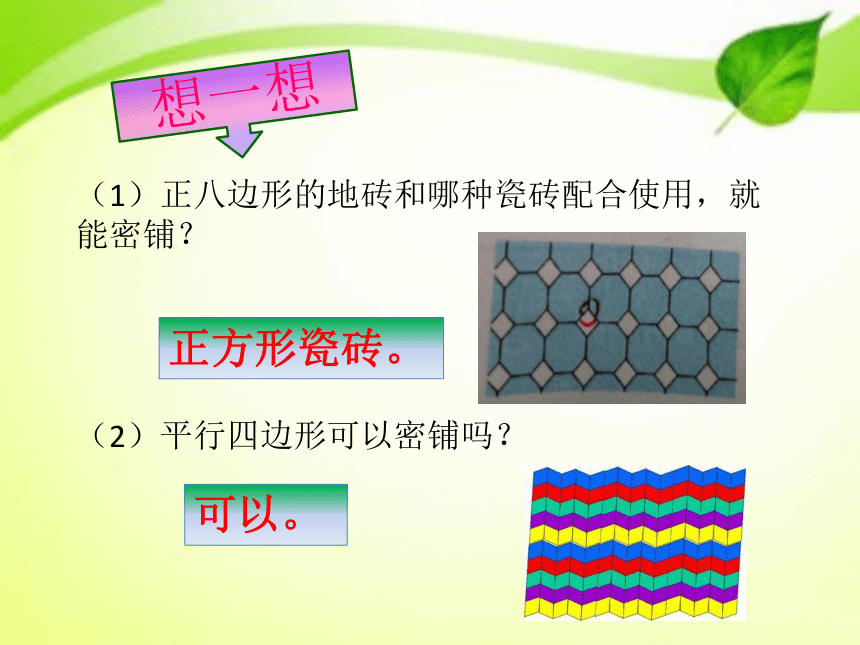
能组成360° 的角。(1)正八边形的地砖和哪种瓷砖配合使用,就能密铺?
(2)平行四边形可以密铺吗?
正方形瓷砖。可以。想一想
1619年——数学家奇柏第一个利用正多边形铺
嵌平面。 1891年——苏联物理学家弗德洛夫发现了十七
种不同的铺砌平面的对称图案。 1924年——数学家波利亚和尼格利重新发现这
个事实。 ??? 最富趣味的是荷兰艺术家埃舍尔与密铺。他到西班牙旅行时,受到阿罕伯拉宫种类繁多的马赛克图案的启发,创造了各种并不局限于几何图形包括鱼、青蛙、狗、人、蜥蜴等密铺作品。这些作品结合了数学与艺术,给人留下深刻印象,更让人对数学产生另一种看法。密铺的历史背景阿罕伯拉宫艺术中的密铺现象艺术中的密铺现象艺术中的密铺现象艺术中的密铺现象生活中的密铺现象客厅生活中的密铺现象水立方生活中的密铺现象高楼大厦自然中的密铺现象菠萝自然中的密铺现象蜂巢自然中的密铺现象乌 龟试一试1、若用同一种平面图形密铺,我们学过的平面图形哪些还能密铺,那些不能?
2、用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能密铺呢?生活中不缺乏美,
缺少的是发现美的眼睛!
——密铺 无论是什么形状的地砖,只要可以将一块地面的中间既不留空隙,也不重叠铺满,就是密铺。观察图片,试着总结什么叫密铺? 用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称作平面图形的镶嵌。猜一猜:用下面的图形可以密铺吗?怎样知道大家的猜测是否正确呢?咱们来试一试吧!正三角形正六边形正八边形结论:用等边三角形和正六边形可以密铺,用正八边形不能密铺。拼成的图形小组合作:试着计算这三种图形一个内角的度数,探究密铺的奥秘。等边三角形: 180 ° ÷3 = 60° 正 六 边 形: ( 6—2)×180 °÷6=120 °正 八 边 形: (8—2)×180 °÷8=135 °结论能密铺图形的关键是:
能组成360° 的角。(1)正八边形的地砖和哪种瓷砖配合使用,就能密铺?
(2)平行四边形可以密铺吗?
正方形瓷砖。可以。想一想
1619年——数学家奇柏第一个利用正多边形铺
嵌平面。 1891年——苏联物理学家弗德洛夫发现了十七
种不同的铺砌平面的对称图案。 1924年——数学家波利亚和尼格利重新发现这
个事实。 ??? 最富趣味的是荷兰艺术家埃舍尔与密铺。他到西班牙旅行时,受到阿罕伯拉宫种类繁多的马赛克图案的启发,创造了各种并不局限于几何图形包括鱼、青蛙、狗、人、蜥蜴等密铺作品。这些作品结合了数学与艺术,给人留下深刻印象,更让人对数学产生另一种看法。密铺的历史背景阿罕伯拉宫艺术中的密铺现象艺术中的密铺现象艺术中的密铺现象艺术中的密铺现象生活中的密铺现象客厅生活中的密铺现象水立方生活中的密铺现象高楼大厦自然中的密铺现象菠萝自然中的密铺现象蜂巢自然中的密铺现象乌 龟试一试1、若用同一种平面图形密铺,我们学过的平面图形哪些还能密铺,那些不能?
2、用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能密铺呢?生活中不缺乏美,
缺少的是发现美的眼睛!
