(新教材)人教B版数学必修二5.1.2数据的数字特征 (78张PPT)
文档属性
| 名称 | (新教材)人教B版数学必修二5.1.2数据的数字特征 (78张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-08 14:58:25 | ||
图片预览











文档简介
课件78张PPT。5.1.2 数据的数字特征 1.最值
一组数据的最值指的是其中的最大值与最小值,最值反映的是这组数最极端的情况.
一般地,最大值用max表示,最小值用min表示.2.平均数
(1)定义:如果给定的一组数是x1,x2,…,xn,则这组数的
平均数为 (x1+x2+…+xn).
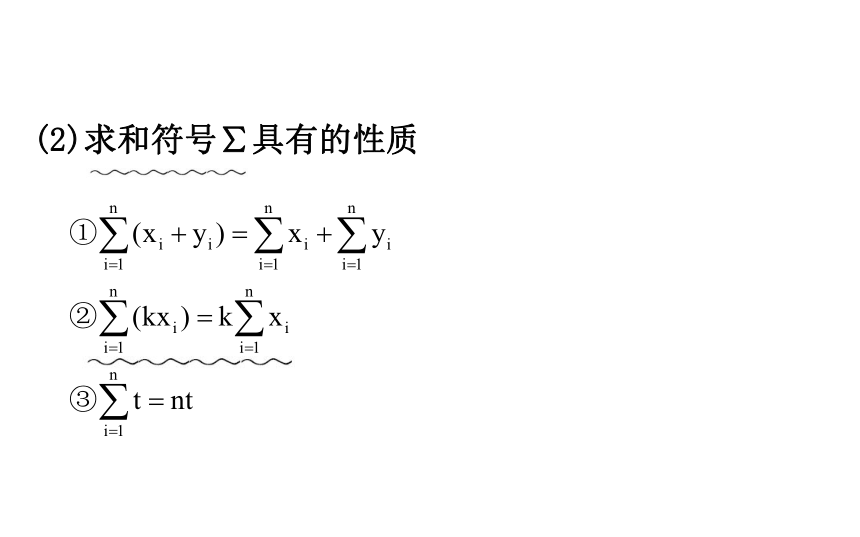
这一公式在数学中常简记为 (2)求和符号∑具有的性质
(3)如果x1,x2,…,xn,的平均数为 ,且a,b为常数,则
ax1+b,ax2+b,…,axn+b的平均数是a +b.【思考】
(1)x5+x6+…+x15如何用符号∑表示?
提示:x5+x6+…+x15= (2)如何证明
提示: =kx1+kx2+…+kxn
=k(x1+x2+…+xn)= .3.中位数
(1)如果一组数有奇数个数,且按照从小到大排列后为
x1,x2,…,x2n+1,则称xn+1为这组数的中位数;
(2)如果一组数有偶数个数,且按照从小到大排列后为
x1,x2,…,x2n,则称 为这组数的中位数.4.百分位数
(1)定义:一组数的p%(p∈(0,100))分位数指的是满足
下列条件的一个数值:至少有p%的数据不大于该值,且
至少有 %的数据不小于该值.(2)计算方法:
设一组数按照从小到大排列后为x1,x2,…,xn,计算
i=np%的值,如果i不是整数,设i0为大于i的最小整数,
取 为p%分位数;如果i是整数,取 为p%分位数.
规定:0分位数是x1(即最小值),100%分位数是xn(即最
大值)【思考】
中位数和百分位数的关系是什么?
提示:中位数是50%分位数.5.众数
一组数据中,某个数据出现的次数称为这个数据的频数,出现次数最多的数据称为这组数据的众数.
6.极差
一组数的极差指的是这组数的最大值减去最小值所得的差.7.方差与标准差
①如果x1,x2,…,xn,的平均数为 ,则方差s2
= ,方差的算术平方根称为标准差.
②如果x1,x2,…,xn,的方差为s2,且a,b为常数,则ax1+b,ax2+b,…,axn+b的方差是a2s2.【思考】
(1)方差和标准差的取值范围是什么?
方差、标准差为0的含义是什么?
提示:标准差、方差的取值范围:[0,+∞).
标准差、方差为0时,样本各数据全相等,表明数据没有波动幅度.(2)方差和标准差是如何反映一组数据的离散程度的?
提示:标准差、方差越大,数据的离散程度越大;标准差、方差越小,数据的离散程度越小.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)对于一组数据来说,众数是唯一的. ( )
(2)中位数在一组数据中是唯一的,且一定是这组数据中的一个数据. ( )(3)x1,x2,x3的平均数为 ,方差为s2,则2x1-1,2x2-1,
2x3-1的平均数为2 -1,方差为4s2-1. ( )
(4)方差、标准差是反映样本波动大小的特征数.( )
提示:(1)×.众数可能不唯一.
(2)×.中位数在一组数据中是唯一的,可能是这组数据中的一个数据,也可能不是这组数据中的数据.
(3)×.2x1-1,2x2-1,2x3-1的平均数为2 -1,方差为4s2,故错误.
(4)√.2.已知一组数据为20,30,40,50,50,60,70,80.其中平
均数、中位数和众数的大小关系是 ( )
A.平均数>中位数>众数 B.平均数<中位数<众数
C.中位数<众数<平均数 D.众数=中位数=平均数
【解析】选D.平均数、中位数、众数皆为50.3.1,3,5,7,9,11,13,15,17,19的25%分位数是 ( )
A.3 B.5 C.6 D.7
【解析】选B.因为数据个数为10,而且10×25%=2.5,因此这组数据的25%分位数为5.4.样本101,98,102,100,99的标准差为 ( )
A. B.0 C.1 D.2
【解析】选A.样本平均数 =100,方差s2=2,
所以标准差s= .类型一 最值、平均数、众数
【典例】某公司员工的月工资情况如表所示:
(1)分别计算该公司员工月工资的最值、平均数、和众数.
(2)你认为用哪个数来代表该公司员工的月工资更合理?【思维·引】(1)依据最值、众数的定义及平均数的计算公式求值.
(2)根据第(1)问的计算结果和实际意义作答.【解析】(1)该公司员工月工资的最大值为8 000元,
最小值为700元,众数为1 000元.平均数为 (8 000
×1+5 000×2+4 000×5+2 000×8+1 000×20+800
×12+700×2)=1 700(元),(2)用众数,因为最大值为8 000元且只有一个,无法代表该公司员工的月工资,平均数受到最大值的影响,也无法代表该公司员工的月工资,每月拿1 000元的员工最多,众数代表该公司员工的月工资最合理.
【内化·悟】
众数和平均数各有什么优缺点?提示:【类题·通】
1.最值和众数的求法
在样本数据中出现次数最多的数据即为众数,最大的数是最大值,最小的数是最小值.2.求平均数的步骤
(1)求和:数据x1,x2,…,xn的和为x1+x2+…+xn.
(2)求平均数:和除以数据的个数n,即x1,x2,…,xn的平均数为 (x1+x2+…+xn).
【习练·破】
某校在一次考试中,甲、乙两班学生的数学成绩统计如下:
选用平均数与众数评估这两个班的成绩.【解析】甲班平均数为 (50×1+60×6+70×12+80×
11+90×15+100×5)=79.6(分),
乙班平均数为 (50×3+60×5+70×15+80×3+90×
13+100×11)=80.2(分),从平均分看成绩较好的是乙班;
甲班众数为90分,乙班众数为70分,从众数看成绩较好
的是甲班.【加练·固】
1.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为
a;x4,x5,…,x10的平均数为b,则样本数据的平均数为
( )
A. B.
C. D. 【解析】选A.因为x1,x2,x3的平均数为a,所以x1,x2,
x3的和为3a,因为x4,x5,…,x10的平均数为b,所以x4,
x5,…,x10的和为7b,则样本数据的和为3a+7b,样本数
据的平均数为 .2.某小区广场上有甲、乙两群市民正在进行晨练,两群市民的年龄如下(单位:岁):
甲群:13,13,14,15,15,15,15,16,17,17;
乙群:54,3,4,4,5,6,6,6,6,56.(1)甲群市民年龄的平均数、中位数和众数各是多少岁?其中哪个统计量能较好地反映甲群市民的年龄特征?
(2)乙群市民年龄的平均数、中位数和众数各是多少岁?其中哪个统计量能较好地反映乙群市民的年龄特征?【解析】(1)甲群市民年龄的平均数为
=15(岁).
中位数为15岁,众数为15岁.
平均数、中位数和众数相等,因此它们都能较好地反映甲群市民的年龄特征.(2)乙群市民年龄的平均数为
=15(岁),
中位数为6岁,众数为6岁.
由于乙群市民大多数是儿童,所以中位数和众数能较好地反映乙群市民的年龄特征,而平均数的可靠性较差.类型二 中位数、百分位数的计算
【典例】1.已知一组数据8,6,4,7,11,6,8,9,10,5,则该组数据的中位数是________.?2.甲、乙两名篮球运动员在随机抽取的12场比赛中的
得分情况如下:甲运动员得分:12,15,20,25,31,31,36,
36,37,39,44,49.
乙运动员得分:8,13,14,16,23,26,28,29,31,38,39,51.
求甲、乙两名运动员得分的25%分位数,75%分位数和
90%分位数. 【思维·引】
1.排序并数出数据总数,依据中位数的定义计算;
2.依据百分位数的定义计算.【解析】1.已知数据从小到大排列为:4,5,6,6,7,8,8,
9,10,11,共10个数,所以中位数是 =7.5.
答案:7.52.两组数据都是12个数,而且12×25%=3,12×75%=9,
12×90%=10.8,
因此,甲运动员得分的25%分位数为 =22.5,
甲运动员得分的75%分位数为 =38,
甲运动员得分的90%分位数为x11=44.乙运动员得分的25%分位数为 =15,
乙运动员得分的75%分位数为 =34.5,
乙运动员得分的90%分位数为x11=39.
【内化·悟】
一组数据的中位数和百分位数一定在数据中出现吗?
提示:当数据个数是偶数个时,中位数是中间两数的平均数,不一定在这些数据中出现.求p%分位数时,若i=np%是整数,也是如此.【类题·通】
1.求中位数的一般步骤
(1)把数据按大小顺序排列.
(2)找出排列后位于中间位置的数据,即为中位数.若中间位置有两个数据,则求出这两个数据的平均数作为中位数.2.求百分位数的一般步骤
(1)排序:按照从小到大排列:x1,x2,…,xn.
(2)计算:求i=np%的值.
(3)求值:【习练·破】
在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:分别求这些运动员成绩的中位数,25%分位数,75%分位数.
【解析】这组数据有17个数,
17×25%=4.25,17×75%=12.75,
这组数据的中位数是x9=1.70,
25%分位数是x5=1.60,75%分位数是x13=1.75.【加练·固】
某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4
则(1)命中环数的中位数为________.?
(2)命中环数的25%分位数为________.?
(3)命中环数的75%分位数为________.?【解析】这组数据按照从小到大排列后为4,4,5,7,7,7,8,9,9,10,
所以命中环数的中位数为 =7.
因为这组数据的个数为10,而且10×25%=2.5,
10×75%=7.5,因此命中环数的25%分位数为x3=5,命中环数的75%分位数为x8=9.
答案:(1)7 (2)5 (3)9
类型三 极差、方差与标准差的计算和应用
角度1 计算问题
【典例】1.设n个数据x1,x2,…,xn的平均数为 ,则其方
差s2= [ ].若数据a1,a2,a3,
a4的方差为3,则数据2a1+1,2a2+1,2a3+1,2a4+1的方差是( )
A.6 B.8 C.10 D.122.甲、乙两种水稻试验品种连续5年的平均单位面积产量如下(单位:吨/公顷).
则甲、乙两种水稻产量的极差分别为________、________.?3.(2019·江苏高考)已知一组数据6,7,8,8,9,10,则该组数据的方差是________.?【思维·引】1.若变量x的方差为s2,y=ax+b,则变量y的方差为a2s2.
2.依据极差的定义求值;
3.首先求得平均数,然后求解方差即可.【解析】1.选D.因为数据a1,a2,a3,a4的方差s2=3,所以数据2a1+1,2a2+1,2a3+1,2a4+1的方差是22·s2=22×3=12.
2.甲种水稻产量的极差为10.2-9.8=0.4,
乙种水稻产量的极差为10.8-9.4=1.4.
答案:0.4 1.43.该组数据的平均数为 =8,
所以该组数据的方差是
[(6-8)2+(7-8)2+(8-8)2+(8-8)2+(9-8)2+(10-8)2]= .
答案: 【素养·探】
在与极差、方差与标准差计算有关的问题中,经常利用核心素养中的数学运算,通过对数据极差、方差和标准差的计算,提高运算能力.
将本例3的数据中增加一个数“8”,方差是多少?与原数据的方差相比有什么变化?【解析】由题意,该组数据的平均数为
=8,
所以该组数据的方差是 [(6-8)2+(7-8)2+(8-8)2+
(8-8)2+(9-8)2+(10-8)2+(8-8)2]= 角度2 应用问题
【典例】某厂准备在甲、乙两位工人中派一名工人参加省活动技能大赛,为此安排甲、乙两位工人在厂实习基地现场进行加工直径为30 mm的零件测试,他俩各加工10个零件,甲、乙两个人加工这10个零件的数据(单位:mm)用如下的数表所示:注:表格中第一列表示的意义是:甲、乙现场加工第一个零件的数据分别是30.0和30.2,第二列表示的意义是:甲、乙现场加工第二个零件的数据分别是30.0和29.8,…,其他列,以此类推. (1)若考虑平均数与完全符合要求的个数,你认为谁的成绩好些?
(2)计算甲、乙两个人的方差,考虑平均数与方差,说明谁的成绩好一些?【思维·引】(1)根据表中数据可求出甲、乙的平均数,分别确定甲、乙的完全符合要求的个数.
(2)分别求出甲和乙的方差,较小的成绩好些.【解析】(1)根据表中数据可得:
所以两人的平均数相等,但甲的完全符合要求的个数为5个,而乙为2个,所以甲的成绩好些.(2)因为 =
且 =
所以 > ,即在平均数相同的情况下,甲的波动性小,所以甲的成绩好些.【类题·通】
1.计算标准差的五个步骤
(1)算出样本数据的平均数 .
(2)算出每个样本数据与样本数据平均数的差:
xi- (i=1,2,3,…,n).(3)算出(2)中xi- (i=1,2,3,…,n)的平方.
(4)算出(3)中n个平方数的平均数,即为样本方差.
(5)算出(4)中方差的算术平方根,即为样本标准差.
2.标准差(方差)的两个作用
(1)标准差(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.
(2)在实际应用中,常常把平均数与标准差结合起来进行决策.在平均值相等的情况下,比较方差或标准差来确定稳定性.【习练·破】
1.已知样本9,10,11,x,y的平均数是10,方差是2,则xy=________.?【解析】由平均数得9+10+11+x+y=50,
所以x+y=20,又由(9-10)2+(10-10)2+(11-10)2+(x-10)2+
(y-10)2=( )2×5=10,
得x2+y2-20(x+y)=-192,
(x+y)2-2xy-20(x+y)=-192,
把x+y=20代入,得xy=96.
答案:962.某校高二年级在一次数学选拔赛中,由于甲、乙两人的竞赛成绩相同,从而决定根据平时在相同条件下进行的六次测试成绩确定出最佳人选,这六次测试的成绩数据如表:求两人比赛成绩的平均数以及方差,并且分析成绩的稳定性,从中选出一位参加数学竞赛.【解析】设甲、乙两人成绩的平均数分别为 , ,
则 =130+ (-3+8+0+7+5+1)=133,
=130+ (3-1+8+4-2+6)=133,
= [(-6)2+52+(-3)2+42+22+(-2)2]= ,
= [02+(-4)2+52+12+(-5)2+32]= .因此,甲与乙的平均数相同,由于乙的方差较小,所以乙的成绩比甲的成绩稳定,选乙参加竞赛比较合适.
【加练·固】甲、乙两台机床同时加工直径为100 mm
的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差.
(2)根据计算结果判断哪台机床加工零件的质量更稳定.【解析】(1) = ×(99+100+98+100+100+103)=100,
= ×(99+100+102+99+100+100)=100.
= ×[(99-100)2+(100-100)2+(98-100)2+
(100-100)2+(100-100)2+(103-100)2]= ,
= ×[(99-100)2+(100-100)2+(102-100)2+
(99-100)2+(100-100)2+(100-100)2]=1.(2)两台机床所加工零件的直径的平均值相同,
又 > ,
所以乙机床加工零件的质量更稳定.
一组数据的最值指的是其中的最大值与最小值,最值反映的是这组数最极端的情况.
一般地,最大值用max表示,最小值用min表示.2.平均数
(1)定义:如果给定的一组数是x1,x2,…,xn,则这组数的
平均数为 (x1+x2+…+xn).
这一公式在数学中常简记为 (2)求和符号∑具有的性质
(3)如果x1,x2,…,xn,的平均数为 ,且a,b为常数,则
ax1+b,ax2+b,…,axn+b的平均数是a +b.【思考】
(1)x5+x6+…+x15如何用符号∑表示?
提示:x5+x6+…+x15= (2)如何证明
提示: =kx1+kx2+…+kxn
=k(x1+x2+…+xn)= .3.中位数
(1)如果一组数有奇数个数,且按照从小到大排列后为
x1,x2,…,x2n+1,则称xn+1为这组数的中位数;
(2)如果一组数有偶数个数,且按照从小到大排列后为
x1,x2,…,x2n,则称 为这组数的中位数.4.百分位数
(1)定义:一组数的p%(p∈(0,100))分位数指的是满足
下列条件的一个数值:至少有p%的数据不大于该值,且
至少有 %的数据不小于该值.(2)计算方法:
设一组数按照从小到大排列后为x1,x2,…,xn,计算
i=np%的值,如果i不是整数,设i0为大于i的最小整数,
取 为p%分位数;如果i是整数,取 为p%分位数.
规定:0分位数是x1(即最小值),100%分位数是xn(即最
大值)【思考】
中位数和百分位数的关系是什么?
提示:中位数是50%分位数.5.众数
一组数据中,某个数据出现的次数称为这个数据的频数,出现次数最多的数据称为这组数据的众数.
6.极差
一组数的极差指的是这组数的最大值减去最小值所得的差.7.方差与标准差
①如果x1,x2,…,xn,的平均数为 ,则方差s2
= ,方差的算术平方根称为标准差.
②如果x1,x2,…,xn,的方差为s2,且a,b为常数,则ax1+b,ax2+b,…,axn+b的方差是a2s2.【思考】
(1)方差和标准差的取值范围是什么?
方差、标准差为0的含义是什么?
提示:标准差、方差的取值范围:[0,+∞).
标准差、方差为0时,样本各数据全相等,表明数据没有波动幅度.(2)方差和标准差是如何反映一组数据的离散程度的?
提示:标准差、方差越大,数据的离散程度越大;标准差、方差越小,数据的离散程度越小.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)对于一组数据来说,众数是唯一的. ( )
(2)中位数在一组数据中是唯一的,且一定是这组数据中的一个数据. ( )(3)x1,x2,x3的平均数为 ,方差为s2,则2x1-1,2x2-1,
2x3-1的平均数为2 -1,方差为4s2-1. ( )
(4)方差、标准差是反映样本波动大小的特征数.( )
提示:(1)×.众数可能不唯一.
(2)×.中位数在一组数据中是唯一的,可能是这组数据中的一个数据,也可能不是这组数据中的数据.
(3)×.2x1-1,2x2-1,2x3-1的平均数为2 -1,方差为4s2,故错误.
(4)√.2.已知一组数据为20,30,40,50,50,60,70,80.其中平
均数、中位数和众数的大小关系是 ( )
A.平均数>中位数>众数 B.平均数<中位数<众数
C.中位数<众数<平均数 D.众数=中位数=平均数
【解析】选D.平均数、中位数、众数皆为50.3.1,3,5,7,9,11,13,15,17,19的25%分位数是 ( )
A.3 B.5 C.6 D.7
【解析】选B.因为数据个数为10,而且10×25%=2.5,因此这组数据的25%分位数为5.4.样本101,98,102,100,99的标准差为 ( )
A. B.0 C.1 D.2
【解析】选A.样本平均数 =100,方差s2=2,
所以标准差s= .类型一 最值、平均数、众数
【典例】某公司员工的月工资情况如表所示:
(1)分别计算该公司员工月工资的最值、平均数、和众数.
(2)你认为用哪个数来代表该公司员工的月工资更合理?【思维·引】(1)依据最值、众数的定义及平均数的计算公式求值.
(2)根据第(1)问的计算结果和实际意义作答.【解析】(1)该公司员工月工资的最大值为8 000元,
最小值为700元,众数为1 000元.平均数为 (8 000
×1+5 000×2+4 000×5+2 000×8+1 000×20+800
×12+700×2)=1 700(元),(2)用众数,因为最大值为8 000元且只有一个,无法代表该公司员工的月工资,平均数受到最大值的影响,也无法代表该公司员工的月工资,每月拿1 000元的员工最多,众数代表该公司员工的月工资最合理.
【内化·悟】
众数和平均数各有什么优缺点?提示:【类题·通】
1.最值和众数的求法
在样本数据中出现次数最多的数据即为众数,最大的数是最大值,最小的数是最小值.2.求平均数的步骤
(1)求和:数据x1,x2,…,xn的和为x1+x2+…+xn.
(2)求平均数:和除以数据的个数n,即x1,x2,…,xn的平均数为 (x1+x2+…+xn).
【习练·破】
某校在一次考试中,甲、乙两班学生的数学成绩统计如下:
选用平均数与众数评估这两个班的成绩.【解析】甲班平均数为 (50×1+60×6+70×12+80×
11+90×15+100×5)=79.6(分),
乙班平均数为 (50×3+60×5+70×15+80×3+90×
13+100×11)=80.2(分),从平均分看成绩较好的是乙班;
甲班众数为90分,乙班众数为70分,从众数看成绩较好
的是甲班.【加练·固】
1.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为
a;x4,x5,…,x10的平均数为b,则样本数据的平均数为
( )
A. B.
C. D. 【解析】选A.因为x1,x2,x3的平均数为a,所以x1,x2,
x3的和为3a,因为x4,x5,…,x10的平均数为b,所以x4,
x5,…,x10的和为7b,则样本数据的和为3a+7b,样本数
据的平均数为 .2.某小区广场上有甲、乙两群市民正在进行晨练,两群市民的年龄如下(单位:岁):
甲群:13,13,14,15,15,15,15,16,17,17;
乙群:54,3,4,4,5,6,6,6,6,56.(1)甲群市民年龄的平均数、中位数和众数各是多少岁?其中哪个统计量能较好地反映甲群市民的年龄特征?
(2)乙群市民年龄的平均数、中位数和众数各是多少岁?其中哪个统计量能较好地反映乙群市民的年龄特征?【解析】(1)甲群市民年龄的平均数为
=15(岁).
中位数为15岁,众数为15岁.
平均数、中位数和众数相等,因此它们都能较好地反映甲群市民的年龄特征.(2)乙群市民年龄的平均数为
=15(岁),
中位数为6岁,众数为6岁.
由于乙群市民大多数是儿童,所以中位数和众数能较好地反映乙群市民的年龄特征,而平均数的可靠性较差.类型二 中位数、百分位数的计算
【典例】1.已知一组数据8,6,4,7,11,6,8,9,10,5,则该组数据的中位数是________.?2.甲、乙两名篮球运动员在随机抽取的12场比赛中的
得分情况如下:甲运动员得分:12,15,20,25,31,31,36,
36,37,39,44,49.
乙运动员得分:8,13,14,16,23,26,28,29,31,38,39,51.
求甲、乙两名运动员得分的25%分位数,75%分位数和
90%分位数. 【思维·引】
1.排序并数出数据总数,依据中位数的定义计算;
2.依据百分位数的定义计算.【解析】1.已知数据从小到大排列为:4,5,6,6,7,8,8,
9,10,11,共10个数,所以中位数是 =7.5.
答案:7.52.两组数据都是12个数,而且12×25%=3,12×75%=9,
12×90%=10.8,
因此,甲运动员得分的25%分位数为 =22.5,
甲运动员得分的75%分位数为 =38,
甲运动员得分的90%分位数为x11=44.乙运动员得分的25%分位数为 =15,
乙运动员得分的75%分位数为 =34.5,
乙运动员得分的90%分位数为x11=39.
【内化·悟】
一组数据的中位数和百分位数一定在数据中出现吗?
提示:当数据个数是偶数个时,中位数是中间两数的平均数,不一定在这些数据中出现.求p%分位数时,若i=np%是整数,也是如此.【类题·通】
1.求中位数的一般步骤
(1)把数据按大小顺序排列.
(2)找出排列后位于中间位置的数据,即为中位数.若中间位置有两个数据,则求出这两个数据的平均数作为中位数.2.求百分位数的一般步骤
(1)排序:按照从小到大排列:x1,x2,…,xn.
(2)计算:求i=np%的值.
(3)求值:【习练·破】
在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如表所示:分别求这些运动员成绩的中位数,25%分位数,75%分位数.
【解析】这组数据有17个数,
17×25%=4.25,17×75%=12.75,
这组数据的中位数是x9=1.70,
25%分位数是x5=1.60,75%分位数是x13=1.75.【加练·固】
某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4
则(1)命中环数的中位数为________.?
(2)命中环数的25%分位数为________.?
(3)命中环数的75%分位数为________.?【解析】这组数据按照从小到大排列后为4,4,5,7,7,7,8,9,9,10,
所以命中环数的中位数为 =7.
因为这组数据的个数为10,而且10×25%=2.5,
10×75%=7.5,因此命中环数的25%分位数为x3=5,命中环数的75%分位数为x8=9.
答案:(1)7 (2)5 (3)9
类型三 极差、方差与标准差的计算和应用
角度1 计算问题
【典例】1.设n个数据x1,x2,…,xn的平均数为 ,则其方
差s2= [ ].若数据a1,a2,a3,
a4的方差为3,则数据2a1+1,2a2+1,2a3+1,2a4+1的方差是( )
A.6 B.8 C.10 D.122.甲、乙两种水稻试验品种连续5年的平均单位面积产量如下(单位:吨/公顷).
则甲、乙两种水稻产量的极差分别为________、________.?3.(2019·江苏高考)已知一组数据6,7,8,8,9,10,则该组数据的方差是________.?【思维·引】1.若变量x的方差为s2,y=ax+b,则变量y的方差为a2s2.
2.依据极差的定义求值;
3.首先求得平均数,然后求解方差即可.【解析】1.选D.因为数据a1,a2,a3,a4的方差s2=3,所以数据2a1+1,2a2+1,2a3+1,2a4+1的方差是22·s2=22×3=12.
2.甲种水稻产量的极差为10.2-9.8=0.4,
乙种水稻产量的极差为10.8-9.4=1.4.
答案:0.4 1.43.该组数据的平均数为 =8,
所以该组数据的方差是
[(6-8)2+(7-8)2+(8-8)2+(8-8)2+(9-8)2+(10-8)2]= .
答案: 【素养·探】
在与极差、方差与标准差计算有关的问题中,经常利用核心素养中的数学运算,通过对数据极差、方差和标准差的计算,提高运算能力.
将本例3的数据中增加一个数“8”,方差是多少?与原数据的方差相比有什么变化?【解析】由题意,该组数据的平均数为
=8,
所以该组数据的方差是 [(6-8)2+(7-8)2+(8-8)2+
(8-8)2+(9-8)2+(10-8)2+(8-8)2]= 角度2 应用问题
【典例】某厂准备在甲、乙两位工人中派一名工人参加省活动技能大赛,为此安排甲、乙两位工人在厂实习基地现场进行加工直径为30 mm的零件测试,他俩各加工10个零件,甲、乙两个人加工这10个零件的数据(单位:mm)用如下的数表所示:注:表格中第一列表示的意义是:甲、乙现场加工第一个零件的数据分别是30.0和30.2,第二列表示的意义是:甲、乙现场加工第二个零件的数据分别是30.0和29.8,…,其他列,以此类推. (1)若考虑平均数与完全符合要求的个数,你认为谁的成绩好些?
(2)计算甲、乙两个人的方差,考虑平均数与方差,说明谁的成绩好一些?【思维·引】(1)根据表中数据可求出甲、乙的平均数,分别确定甲、乙的完全符合要求的个数.
(2)分别求出甲和乙的方差,较小的成绩好些.【解析】(1)根据表中数据可得:
所以两人的平均数相等,但甲的完全符合要求的个数为5个,而乙为2个,所以甲的成绩好些.(2)因为 =
且 =
所以 > ,即在平均数相同的情况下,甲的波动性小,所以甲的成绩好些.【类题·通】
1.计算标准差的五个步骤
(1)算出样本数据的平均数 .
(2)算出每个样本数据与样本数据平均数的差:
xi- (i=1,2,3,…,n).(3)算出(2)中xi- (i=1,2,3,…,n)的平方.
(4)算出(3)中n个平方数的平均数,即为样本方差.
(5)算出(4)中方差的算术平方根,即为样本标准差.
2.标准差(方差)的两个作用
(1)标准差(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.
(2)在实际应用中,常常把平均数与标准差结合起来进行决策.在平均值相等的情况下,比较方差或标准差来确定稳定性.【习练·破】
1.已知样本9,10,11,x,y的平均数是10,方差是2,则xy=________.?【解析】由平均数得9+10+11+x+y=50,
所以x+y=20,又由(9-10)2+(10-10)2+(11-10)2+(x-10)2+
(y-10)2=( )2×5=10,
得x2+y2-20(x+y)=-192,
(x+y)2-2xy-20(x+y)=-192,
把x+y=20代入,得xy=96.
答案:962.某校高二年级在一次数学选拔赛中,由于甲、乙两人的竞赛成绩相同,从而决定根据平时在相同条件下进行的六次测试成绩确定出最佳人选,这六次测试的成绩数据如表:求两人比赛成绩的平均数以及方差,并且分析成绩的稳定性,从中选出一位参加数学竞赛.【解析】设甲、乙两人成绩的平均数分别为 , ,
则 =130+ (-3+8+0+7+5+1)=133,
=130+ (3-1+8+4-2+6)=133,
= [(-6)2+52+(-3)2+42+22+(-2)2]= ,
= [02+(-4)2+52+12+(-5)2+32]= .因此,甲与乙的平均数相同,由于乙的方差较小,所以乙的成绩比甲的成绩稳定,选乙参加竞赛比较合适.
【加练·固】甲、乙两台机床同时加工直径为100 mm
的零件,为检验质量,各从中抽取6件测量,数据为:
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差.
(2)根据计算结果判断哪台机床加工零件的质量更稳定.【解析】(1) = ×(99+100+98+100+100+103)=100,
= ×(99+100+102+99+100+100)=100.
= ×[(99-100)2+(100-100)2+(98-100)2+
(100-100)2+(100-100)2+(103-100)2]= ,
= ×[(99-100)2+(100-100)2+(102-100)2+
(99-100)2+(100-100)2+(100-100)2]=1.(2)两台机床所加工零件的直径的平均值相同,
又 > ,
所以乙机床加工零件的质量更稳定.
