(新教材)人教B版数学必修二6.2.3平面向量的坐标及其运算(74张PPT)
文档属性
| 名称 | (新教材)人教B版数学必修二6.2.3平面向量的坐标及其运算(74张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-08 00:00:00 | ||
图片预览











文档简介
课件74张PPT。6.2.3
平面向量的坐标及其运算1.平面向量的坐标
(1)向量的垂直:平面上的两个非零向量a,b,如果它们所在的直线互相垂直,则称向量a,b垂直,记作a⊥b.规定零向量与任意向量都垂直.(2)向量的正交分解:如果平面向量的基底{e1,e2}中,e1⊥e2,则称这组基底为正交基底,在正交基底下向量的分解称为向量的正交分解.
(3)向量的坐标:给定平面内两个相互垂直的单位向量e1,e2,对于平面内的向量a,如果a=xe1+ye2,则称(x,y)为向量a的坐标,记作a=(x,y). 【思考】
(1)正交分解与平面向量基本定理有何联系?
提示:正交分解是平面向量基本定理的特殊形式(基底垂直时). (2)平面中,若以e1的方向为x轴的正方向,以e2的方向为y轴的正方向,则e1,e2的坐标分别是什么?
提示:e1=(1,0),e2=(0,1).(3)向量的坐标就是其终点的坐标吗?
提示:不一定,以坐标原点O为始点的向量坐标就是该向量的终点坐标,如果向量不是以坐标原点为始点,则向量坐标就跟终点坐标不同,而对同一向量或相等向量(向量坐标相同),若选择不同的始点坐标,则终点坐标也不同. 2.平面上向量的运算与坐标的关系
若a=(x1,y1),b=(x2,y2),λ∈R,则:
(1)a+b=(x1+x2,y1+y2),
(2)a-b=(x1-x2,y1-y2),
(3)λa=(λx1,λy1).(4)向量相等的充要条件:a=b?x1=x2且y1=y2.
(5)模长公式:|a|= 【思考】
(1)平面向量的加法坐标运算法则若写成“若a= (x1,y1),b=(x2,y2),则a+b=(y1+y2,x1+x2)”可以吗?
提示:不可以,两向量的横坐标之和作为和向量的横坐标,纵坐标之和作为和向量的纵坐标. (2)如果μ,v是两个实数,那么μa+vb,μa-vb的坐标如何表示?
提示:μa+vb=(μx1+vx2,μy1+vy2),
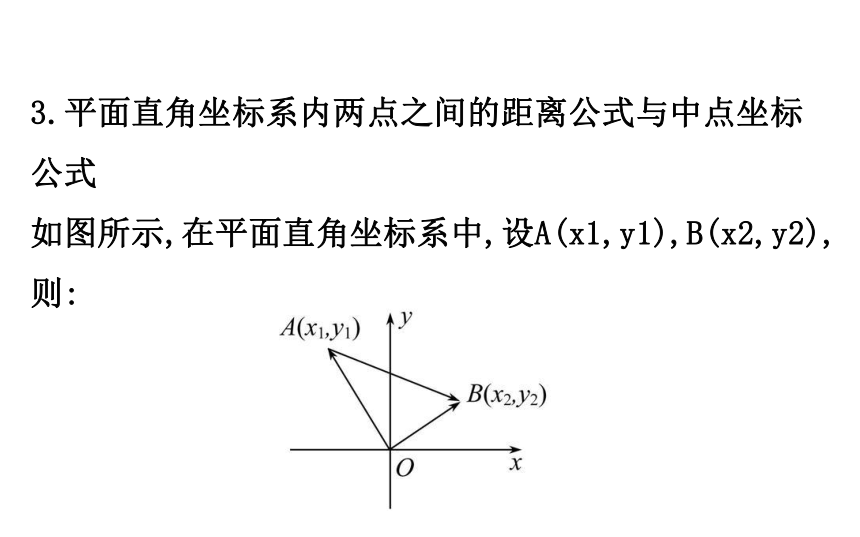
μa-vb=(μx1-vx2,μy1-vy2).3.平面直角坐标系内两点之间的距离公式与中点坐标公式
如图所示,在平面直角坐标系中,设A(x1,y1),B(x2,y2),则:(1)向量 =(x1,y1), =(x2,y2),向量 =(x2-x1,
y2-y1).
(2)它们之间的距离:AB=| |=
(3)设AB的中点M(x,y),则x= 【思考】
“若A(x1,y1),B(x2,y2),则 =(x1-x2,y1-y2)”对吗?
提示:不对,应该用终点坐标减去始点坐标. 4.向量平行的坐标表示
设向量a=(x1,y1),b=(x2,y2),则a∥b?x2y1=x1y2.【思考】
把x1y2-x2y1=0写成x1y1-x2y2=0或x1x2-y1y2=0可以吗?怎样记忆此公式的表达式?
提示:写成x1y1-x2y2=0或x1x2-y1y2=0都是不对的,这一公式可简记为:纵横交错积相减.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)两个向量的终点不同,则这两个向量的坐标一定不同. ( )
(2)当向量的始点在坐标原点时,向量的坐标就是向量终点的坐标. ( ) (3)两向量差的坐标与两向量的顺序无关. ( )
(4)向量(2,3)与向量(-4,-6)同向. ( )【提示】(1)×.对于同一个向量,无论位置在哪里,坐标都一样.
(2)√.根据向量的坐标表示,当始点在原点时,终点与始点坐标之差等于终点坐标.
(3)×.根据两向量差的运算,两向量差的坐标与两向量的顺序有关.(4)×.因为(-4,-6)=-2(2,3),所以向量(2,3)与向量(-4,-6)反向.2.已知a=(2,1),b=(3,-2),则3a-2b的坐标是( )
A.(0,-7) B.(0,7)
C.(-1,3) D.(12,-1)【解析】选B.3a-2b=3(2,1)-2(3,-2)=(6,3)-(6,-4)
=(0,7).3.下列向量组中,不共线的向量组是 ( )
A.e1=(0,0),e2=(1,-2)
B.e1=(-1,2),e2=(5,7)
C.e1=(3,5),e2=(6,10)
D.e1=(2,-3),e2= 【解析】选B.A选项中,e1=0e2,C选项中,e2=2e1,D选项
中,e2= e1,两向量都共线,只有B选项中不共线.类型一 向量的坐标表示
【典例】1.已知e1,e2是平面内两个相互垂直的单位向量,且a=4e1-3e2,则向量a的坐标为 ( )
A.(4e1,3e2) B.(4e1,-3e2)
C.(4,3) D.(4,-3)2.已知O是坐标原点,点A在第二象限,| |=6,∠xOA= 150°,向量 的坐标为________.?
【思维·引】1.利用向量坐标的定义解决.
2.画出图形,用解三角形的方法求点的坐标,进而求向量的坐标.【解析】1.选D.由向量坐标的定义可知,向量a的坐标
为(4,-3).
2.设点A(x,y),则x=| |cos 150°=6cos 150°=
-3 ,y=| |sin 150°=6sin 150°=3,即A(-3 ,
3),所以 =(-3 ,3).
答案:(-3 ,3)【内化·悟】
1.如果一个向量的始点为原点,那么怎样求该向量的坐标?
提示:求出终点坐标,终点坐标即向量的坐标.2.如果一个向量的始点不是原点,要求它的坐标,需要求哪些量?
提示:需要求表示该向量的有向线段的始点和终点的坐标.【类题·通】
求向量坐标的方法
(1)定义法:将向量用两个相互垂直的单位向量e1,e2表示出来.(2)平移法:把向量的始点移至坐标原点,终点坐标即为向量的坐标.
(3)求差法:先求出这个向量的始点、终点坐标,再运用终点坐标减去始点坐标即得该向量的坐标. 【习练·破】
已知边长为2的正三角形ABC,顶点A在坐标原点,AB边
在x轴上,C在第一象限,D为AC的中点,分别求向量
的坐标. 【解析】如图,正三角形ABC的边长为2,则顶点A(0,0),B(2,0),C(2cos 60°,2sin 60°),
所以
所以 【加练·固】
如图,已知边长为1的正方形ABCD中,顶点A在坐标原
点,AB与x轴正半轴成30°角.求点B及点D的坐标及
的坐标.【解析】由题知B,D分别是30°,120°角的终边与以O为圆心的单位圆的交点.设B(x1,y1),D(x2,y2).
由三角函数的定义,得
x1=cos 30°= ,y1=sin 30°= ,所以B
x2=cos 120°=- ,y2=sin 120°= ,所以D
所以 类型二 向量的坐标运算
【典例】1.(2019·邢台高一检测)已知点A(0,1),
B(3,2),向量 =(-3,-3),则向量 = ( )
A.(3,2) B.(-3,-2) C.(-1,-2) D.(1,2)2.已知M(3,-2),N(-5,-1), 则| |=
________,点P的坐标为________.?
【思维·引】1.由 计算.
2.先用模长公式求模,再设出点P的坐标,利用坐标运算及向量相等的条件构造方程组求解.【解析】1.选B.因为A(0,1),B(3,2),所以 =(3,1),所以
2.设P(x,y), =(x-3,y+2), =(-8,1),
所以 所以
所以
答案: 【内化·悟】
本例1中,可否先求出点C的坐标,进而再求向量 ?提示:可以,设点C的坐标为(x,y).
因为A(0,1), =(-3,-3),
所以
所以点C的坐标为(-3,-2).
又B(3,2),所以 =(-6,-4), =(-3,-2).【类题·通】
平面向量坐标运算的技巧
(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.(2)若已知有向线段两端点的坐标,则可先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可完全类比数的运算进行. 【习练·破】
若A,B,C三点的坐标分别为(2,-4),(0,6),(-8,10),
求 的坐标.【解析】因为 =(-2,10), =(-8,4), =(-10,14),
所以 +2 =(-2,10)+2(-8,4)
=(-2,10)+(-16,8)=(-18,18),
=(-8,4)- (-10,14)
=(-8,4)-(-5,7)=(-3,-3).类型三 向量共线的坐标表示
角度1 向量共线的判定
【典例】已知两点A(4,1),B(7,-3),则与向量 共线的单位向量是 ( )【思维·引】利用向量共线的坐标表示判断.
【解析】选B.因为 =(7,-3)-(4,1)=(3,-4),由向量
共线的条件可知,A,B,C选项中的向量均与 共线,但
A,C中向量不是单位向量.【素养·探】
本题主要考查向量共线坐标表示的应用,突出考查数学运算的核心素养.
本例选项中有哪些向量与 共线,其中有反向的向量吗?提示:因为 =(7,-3)-(4,1)=(3,-4),故A.(3,-4),
B. C.(-6,8)均与 共线,且B,C选项的向量
与 反向.角度2 利用向量共线的坐标表示求参数
【典例】若向量a=(1,1),b=(x,1),u=a+2b,v=2a-b.
(1)若u=3v,求x.
(2)若u∥v,求x,并判断u与v是同向还是反向.【思维·引】(1)先求出u与v的坐标,再由向量相等可求x.
(2)由u∥v求出x,再将u用v表示出来,写成u=λv的形式,根据λ的值判断同向还是反向.【解析】因为a=(1,1),b=(x,1),
所以u=(1,1)+2(x,1)=(1,1)+(2x,2)=(2x+1,3);
v=2(1,1)-(x,1)=(2-x,1).(1)u=3v?(2x+1,3)=3(2-x,1)?(2x+1,3)=(6-3x,3) ?2x+1=6-3x.解得x=1.
(2)u∥v?(2x+1)×1-3(2-x)=0.解得x=1.
所以u=(3,3),v=(1,1).所以u与v同向. 【内化·悟】
1.由共线的坐标条件求参数的解题步骤是怎样的?
提示:(1)分别写出共线的两个向量的坐标.
(2)通过共线条件列出方程(组).
(3)解方程(组)求出参数.2.如何判断共线的向量u与v是同向还是反向?
提示:写成u=λv的形式,若λ>0,同向,若λ<0,反向.角度3 三点共线问题
【典例】已知A(1,-3),B 且A,B,C三点共线,则C的坐标可以是 ( )
A.(-9,1) B.(9,-1)
C.(9,1) D.(-9,-1)【思维·引】设出点C的坐标,因为A,B,C三点共线,写
出向量 (或 ),由向量共线的条件结合选项
求解.【解析】选C.设点C的坐标是(x,y),
因为A,B,C三点共线,所以
因为
=(x,y)-(1,-3)=(x-1,y+3),
所以7(y+3)- (x-1)=0,整理得x-2y=7,
经检验可知点(9,1)符合要求.【发散·拓】求证:若A(x1,y1),B(x2,y2),C(x3,y3),则A,B,C三点共线的条件为(x2-x1)(y3-y1)-(x3-x1)(y2-y1)=0.证明:若三点A(x1,y1),B(x2,y2),C(x3,y3)共线,则有
从而(x2-x1,y2-y1)=λ(x3-x2,y3-y2),即(x2-
x1)(y3-y2)=(x3-x2)(y2-y1),显然由 ,也可得
到(x2-x1)(y3-y1)=(x3-x1)(y2-y1),或由 ,得
到(x3-x2)(y3-y1)=(x3-x1)(y3-y2).当这些条件中有一
个成立时,A,B,C三点共线.【延伸·练】若A(3,-6),B(-5,2),C(6,y)三点共线,则y= ( )
A.13 B.-13 C.9 D.-9【解析】选D.因为A,B,C三点共线,
所以(-5-3)(y+6)-(6-3)(2+6)=0,
所以y=-9.【类题·通】
1.利用向量共线的条件处理求值问题的思路
(1)利用共线向量定理a=λb(b≠0)列方程组求解.
(2)利用向量平行的坐标表达式x1y2-x2y1=0直接求解.2.三点共线问题的实质是向量共线问题,只要利用三点构造出两个向量,再使用向量共线的条件解决即可.【习练·破】
(2018·全国卷Ⅲ)已知向量a=(1,2),b=(2,-2),c= (1,λ).若c∥(2a+b),则λ=________.?【解析】2a+b=2(1,2)+(2,-2)=(4,2),c=(1,λ),
由c∥(2a+b),得4λ-2=0,得λ= .
答案: 【加练·固】
已知a=(1,2),b=(-3,2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向?【解析】方法一:ka+b=k(1,2)+(-3,2)=(k-3,2k+2),
a-3b=(1,2)-3(-3,2)=(10,-4),
当ka+b与a-3b平行时,存在唯一实数λ,
使ka+b=λ(a-3b).由(k-3,2k+2)=λ(10,-4),
所以 解得k=λ=- .
当k=- 时,ka+b与a-3b平行,
这时ka+b=- a+b=- (a-3b),
因为λ=- <0,
所以ka+b与a-3b反向.方法二:由题知ka+b=(k-3,2k+2),
a-3b=(10,-4),因为ka+b与a-3b平行,
所以(k-3)×(-4)-10×(2k+2)=0,解得k=- .
这时ka+b= =- (a-3b).
所以当k=- 时,ka+b与a-3b平行,并且反向.
平面向量的坐标及其运算1.平面向量的坐标
(1)向量的垂直:平面上的两个非零向量a,b,如果它们所在的直线互相垂直,则称向量a,b垂直,记作a⊥b.规定零向量与任意向量都垂直.(2)向量的正交分解:如果平面向量的基底{e1,e2}中,e1⊥e2,则称这组基底为正交基底,在正交基底下向量的分解称为向量的正交分解.
(3)向量的坐标:给定平面内两个相互垂直的单位向量e1,e2,对于平面内的向量a,如果a=xe1+ye2,则称(x,y)为向量a的坐标,记作a=(x,y). 【思考】
(1)正交分解与平面向量基本定理有何联系?
提示:正交分解是平面向量基本定理的特殊形式(基底垂直时). (2)平面中,若以e1的方向为x轴的正方向,以e2的方向为y轴的正方向,则e1,e2的坐标分别是什么?
提示:e1=(1,0),e2=(0,1).(3)向量的坐标就是其终点的坐标吗?
提示:不一定,以坐标原点O为始点的向量坐标就是该向量的终点坐标,如果向量不是以坐标原点为始点,则向量坐标就跟终点坐标不同,而对同一向量或相等向量(向量坐标相同),若选择不同的始点坐标,则终点坐标也不同. 2.平面上向量的运算与坐标的关系
若a=(x1,y1),b=(x2,y2),λ∈R,则:
(1)a+b=(x1+x2,y1+y2),
(2)a-b=(x1-x2,y1-y2),
(3)λa=(λx1,λy1).(4)向量相等的充要条件:a=b?x1=x2且y1=y2.
(5)模长公式:|a|= 【思考】
(1)平面向量的加法坐标运算法则若写成“若a= (x1,y1),b=(x2,y2),则a+b=(y1+y2,x1+x2)”可以吗?
提示:不可以,两向量的横坐标之和作为和向量的横坐标,纵坐标之和作为和向量的纵坐标. (2)如果μ,v是两个实数,那么μa+vb,μa-vb的坐标如何表示?
提示:μa+vb=(μx1+vx2,μy1+vy2),
μa-vb=(μx1-vx2,μy1-vy2).3.平面直角坐标系内两点之间的距离公式与中点坐标公式
如图所示,在平面直角坐标系中,设A(x1,y1),B(x2,y2),则:(1)向量 =(x1,y1), =(x2,y2),向量 =(x2-x1,
y2-y1).
(2)它们之间的距离:AB=| |=
(3)设AB的中点M(x,y),则x= 【思考】
“若A(x1,y1),B(x2,y2),则 =(x1-x2,y1-y2)”对吗?
提示:不对,应该用终点坐标减去始点坐标. 4.向量平行的坐标表示
设向量a=(x1,y1),b=(x2,y2),则a∥b?x2y1=x1y2.【思考】
把x1y2-x2y1=0写成x1y1-x2y2=0或x1x2-y1y2=0可以吗?怎样记忆此公式的表达式?
提示:写成x1y1-x2y2=0或x1x2-y1y2=0都是不对的,这一公式可简记为:纵横交错积相减.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)两个向量的终点不同,则这两个向量的坐标一定不同. ( )
(2)当向量的始点在坐标原点时,向量的坐标就是向量终点的坐标. ( ) (3)两向量差的坐标与两向量的顺序无关. ( )
(4)向量(2,3)与向量(-4,-6)同向. ( )【提示】(1)×.对于同一个向量,无论位置在哪里,坐标都一样.
(2)√.根据向量的坐标表示,当始点在原点时,终点与始点坐标之差等于终点坐标.
(3)×.根据两向量差的运算,两向量差的坐标与两向量的顺序有关.(4)×.因为(-4,-6)=-2(2,3),所以向量(2,3)与向量(-4,-6)反向.2.已知a=(2,1),b=(3,-2),则3a-2b的坐标是( )
A.(0,-7) B.(0,7)
C.(-1,3) D.(12,-1)【解析】选B.3a-2b=3(2,1)-2(3,-2)=(6,3)-(6,-4)
=(0,7).3.下列向量组中,不共线的向量组是 ( )
A.e1=(0,0),e2=(1,-2)
B.e1=(-1,2),e2=(5,7)
C.e1=(3,5),e2=(6,10)
D.e1=(2,-3),e2= 【解析】选B.A选项中,e1=0e2,C选项中,e2=2e1,D选项
中,e2= e1,两向量都共线,只有B选项中不共线.类型一 向量的坐标表示
【典例】1.已知e1,e2是平面内两个相互垂直的单位向量,且a=4e1-3e2,则向量a的坐标为 ( )
A.(4e1,3e2) B.(4e1,-3e2)
C.(4,3) D.(4,-3)2.已知O是坐标原点,点A在第二象限,| |=6,∠xOA= 150°,向量 的坐标为________.?
【思维·引】1.利用向量坐标的定义解决.
2.画出图形,用解三角形的方法求点的坐标,进而求向量的坐标.【解析】1.选D.由向量坐标的定义可知,向量a的坐标
为(4,-3).
2.设点A(x,y),则x=| |cos 150°=6cos 150°=
-3 ,y=| |sin 150°=6sin 150°=3,即A(-3 ,
3),所以 =(-3 ,3).
答案:(-3 ,3)【内化·悟】
1.如果一个向量的始点为原点,那么怎样求该向量的坐标?
提示:求出终点坐标,终点坐标即向量的坐标.2.如果一个向量的始点不是原点,要求它的坐标,需要求哪些量?
提示:需要求表示该向量的有向线段的始点和终点的坐标.【类题·通】
求向量坐标的方法
(1)定义法:将向量用两个相互垂直的单位向量e1,e2表示出来.(2)平移法:把向量的始点移至坐标原点,终点坐标即为向量的坐标.
(3)求差法:先求出这个向量的始点、终点坐标,再运用终点坐标减去始点坐标即得该向量的坐标. 【习练·破】
已知边长为2的正三角形ABC,顶点A在坐标原点,AB边
在x轴上,C在第一象限,D为AC的中点,分别求向量
的坐标. 【解析】如图,正三角形ABC的边长为2,则顶点A(0,0),B(2,0),C(2cos 60°,2sin 60°),
所以
所以 【加练·固】
如图,已知边长为1的正方形ABCD中,顶点A在坐标原
点,AB与x轴正半轴成30°角.求点B及点D的坐标及
的坐标.【解析】由题知B,D分别是30°,120°角的终边与以O为圆心的单位圆的交点.设B(x1,y1),D(x2,y2).
由三角函数的定义,得
x1=cos 30°= ,y1=sin 30°= ,所以B
x2=cos 120°=- ,y2=sin 120°= ,所以D
所以 类型二 向量的坐标运算
【典例】1.(2019·邢台高一检测)已知点A(0,1),
B(3,2),向量 =(-3,-3),则向量 = ( )
A.(3,2) B.(-3,-2) C.(-1,-2) D.(1,2)2.已知M(3,-2),N(-5,-1), 则| |=
________,点P的坐标为________.?
【思维·引】1.由 计算.
2.先用模长公式求模,再设出点P的坐标,利用坐标运算及向量相等的条件构造方程组求解.【解析】1.选B.因为A(0,1),B(3,2),所以 =(3,1),所以
2.设P(x,y), =(x-3,y+2), =(-8,1),
所以 所以
所以
答案: 【内化·悟】
本例1中,可否先求出点C的坐标,进而再求向量 ?提示:可以,设点C的坐标为(x,y).
因为A(0,1), =(-3,-3),
所以
所以点C的坐标为(-3,-2).
又B(3,2),所以 =(-6,-4), =(-3,-2).【类题·通】
平面向量坐标运算的技巧
(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.(2)若已知有向线段两端点的坐标,则可先求出向量的坐标,然后再进行向量的坐标运算.
(3)向量的线性坐标运算可完全类比数的运算进行. 【习练·破】
若A,B,C三点的坐标分别为(2,-4),(0,6),(-8,10),
求 的坐标.【解析】因为 =(-2,10), =(-8,4), =(-10,14),
所以 +2 =(-2,10)+2(-8,4)
=(-2,10)+(-16,8)=(-18,18),
=(-8,4)- (-10,14)
=(-8,4)-(-5,7)=(-3,-3).类型三 向量共线的坐标表示
角度1 向量共线的判定
【典例】已知两点A(4,1),B(7,-3),则与向量 共线的单位向量是 ( )【思维·引】利用向量共线的坐标表示判断.
【解析】选B.因为 =(7,-3)-(4,1)=(3,-4),由向量
共线的条件可知,A,B,C选项中的向量均与 共线,但
A,C中向量不是单位向量.【素养·探】
本题主要考查向量共线坐标表示的应用,突出考查数学运算的核心素养.
本例选项中有哪些向量与 共线,其中有反向的向量吗?提示:因为 =(7,-3)-(4,1)=(3,-4),故A.(3,-4),
B. C.(-6,8)均与 共线,且B,C选项的向量
与 反向.角度2 利用向量共线的坐标表示求参数
【典例】若向量a=(1,1),b=(x,1),u=a+2b,v=2a-b.
(1)若u=3v,求x.
(2)若u∥v,求x,并判断u与v是同向还是反向.【思维·引】(1)先求出u与v的坐标,再由向量相等可求x.
(2)由u∥v求出x,再将u用v表示出来,写成u=λv的形式,根据λ的值判断同向还是反向.【解析】因为a=(1,1),b=(x,1),
所以u=(1,1)+2(x,1)=(1,1)+(2x,2)=(2x+1,3);
v=2(1,1)-(x,1)=(2-x,1).(1)u=3v?(2x+1,3)=3(2-x,1)?(2x+1,3)=(6-3x,3) ?2x+1=6-3x.解得x=1.
(2)u∥v?(2x+1)×1-3(2-x)=0.解得x=1.
所以u=(3,3),v=(1,1).所以u与v同向. 【内化·悟】
1.由共线的坐标条件求参数的解题步骤是怎样的?
提示:(1)分别写出共线的两个向量的坐标.
(2)通过共线条件列出方程(组).
(3)解方程(组)求出参数.2.如何判断共线的向量u与v是同向还是反向?
提示:写成u=λv的形式,若λ>0,同向,若λ<0,反向.角度3 三点共线问题
【典例】已知A(1,-3),B 且A,B,C三点共线,则C的坐标可以是 ( )
A.(-9,1) B.(9,-1)
C.(9,1) D.(-9,-1)【思维·引】设出点C的坐标,因为A,B,C三点共线,写
出向量 (或 ),由向量共线的条件结合选项
求解.【解析】选C.设点C的坐标是(x,y),
因为A,B,C三点共线,所以
因为
=(x,y)-(1,-3)=(x-1,y+3),
所以7(y+3)- (x-1)=0,整理得x-2y=7,
经检验可知点(9,1)符合要求.【发散·拓】求证:若A(x1,y1),B(x2,y2),C(x3,y3),则A,B,C三点共线的条件为(x2-x1)(y3-y1)-(x3-x1)(y2-y1)=0.证明:若三点A(x1,y1),B(x2,y2),C(x3,y3)共线,则有
从而(x2-x1,y2-y1)=λ(x3-x2,y3-y2),即(x2-
x1)(y3-y2)=(x3-x2)(y2-y1),显然由 ,也可得
到(x2-x1)(y3-y1)=(x3-x1)(y2-y1),或由 ,得
到(x3-x2)(y3-y1)=(x3-x1)(y3-y2).当这些条件中有一
个成立时,A,B,C三点共线.【延伸·练】若A(3,-6),B(-5,2),C(6,y)三点共线,则y= ( )
A.13 B.-13 C.9 D.-9【解析】选D.因为A,B,C三点共线,
所以(-5-3)(y+6)-(6-3)(2+6)=0,
所以y=-9.【类题·通】
1.利用向量共线的条件处理求值问题的思路
(1)利用共线向量定理a=λb(b≠0)列方程组求解.
(2)利用向量平行的坐标表达式x1y2-x2y1=0直接求解.2.三点共线问题的实质是向量共线问题,只要利用三点构造出两个向量,再使用向量共线的条件解决即可.【习练·破】
(2018·全国卷Ⅲ)已知向量a=(1,2),b=(2,-2),c= (1,λ).若c∥(2a+b),则λ=________.?【解析】2a+b=2(1,2)+(2,-2)=(4,2),c=(1,λ),
由c∥(2a+b),得4λ-2=0,得λ= .
答案: 【加练·固】
已知a=(1,2),b=(-3,2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向?【解析】方法一:ka+b=k(1,2)+(-3,2)=(k-3,2k+2),
a-3b=(1,2)-3(-3,2)=(10,-4),
当ka+b与a-3b平行时,存在唯一实数λ,
使ka+b=λ(a-3b).由(k-3,2k+2)=λ(10,-4),
所以 解得k=λ=- .
当k=- 时,ka+b与a-3b平行,
这时ka+b=- a+b=- (a-3b),
因为λ=- <0,
所以ka+b与a-3b反向.方法二:由题知ka+b=(k-3,2k+2),
a-3b=(10,-4),因为ka+b与a-3b平行,
所以(k-3)×(-4)-10×(2k+2)=0,解得k=- .
这时ka+b= =- (a-3b).
所以当k=- 时,ka+b与a-3b平行,并且反向.
