六年级上册数学课件-分数除法 人教新课标(2019秋) (共 38 张ppt)
文档属性
| 名称 | 六年级上册数学课件-分数除法 人教新课标(2019秋) (共 38 张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-06 09:00:21 | ||
图片预览








文档简介
(共38张PPT)
2
0
1
9
分数除法
课程大纲
Teaching Programme
倒数的认识
分数除法法则
分数方程
解决问题
01
倒数的认识
Teaching background
倒数的认识 Teaching background
乘积是1的两个数,互为倒数。
那么a、b互为倒数;
a是b的倒数,b是a的倒数。
注:① 互为倒数的两个数,可以是整数,也可以是分数,小数。
② 倒数是一种关系,不是一种数,不能说a是倒数,b是倒数。
③ “1”的倒数是它本身。
④ “0”没有倒数
练习 Teaching background
判断对错
1、因为a×b=1,所以a、b互为倒数。
2、因为a×b=1,所以a、b都是倒数。
3、因为a×b=1,所以a是b的倒数,b是a的倒数。
4、因为5×0.2=1,所以他们互为倒数。
6、因为0.5+0.5=1,所以他们互为倒数。
7、因为1的倒数是1,所以0的倒数是0.
( )
( )
( )
( )
( )
( )
求倒数 Teaching background
求倒数
整数的倒数
分数的倒数
小数的倒数
带分数的倒数
求倒数 Teaching background
整数的倒数:求3的倒数。
本身做分母,分子是1。
a的倒数是
求倒数 Teaching background
分数的倒数:求 的倒数。
分数的倒数就是,
分子分母倒过来。
的倒数是
1
1
1
1
求倒数 Teaching background
带分数的倒数:求 的倒数。
现将带分数化成假分数,
再求假分数的倒数。
7
10
求倒数 Teaching background
小数的倒数:求 的倒数。
现将小数化成分数,
再求分数的倒数。
4
3
求倒数 Teaching background
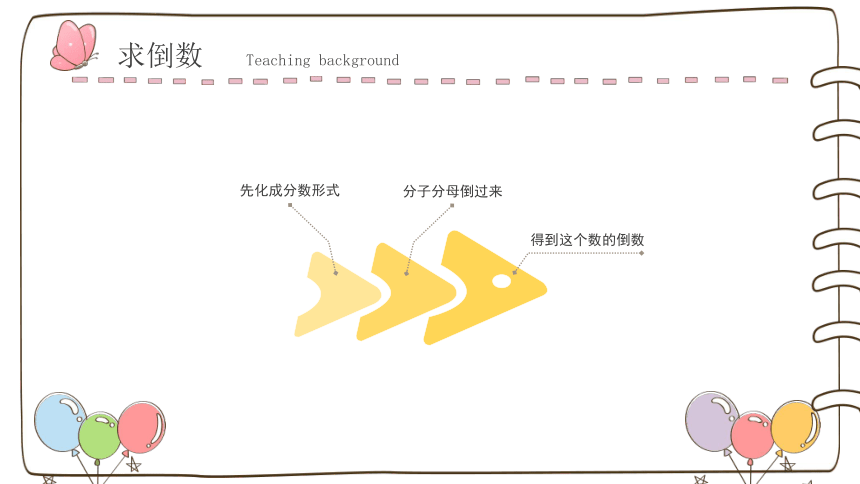
得到这个数的倒数
分子分母倒过来
先化成分数形式
补充 Teaching background
1、真分数的倒数是假分数,大于1,大于它本身。
2、假分数的倒数是真分数,小于1 ,小于它本身。
3、带分数的倒数是真分数,小于1,小于它本身。
4、大于1的数,倒数小于1,小于它本身。
6、小于1 的数,倒数大于1,大于它本身。
补充
02
分数除法
The teaching process
分数除法 The teaching process
除以一个数等于乘以这个数的倒数,零除外。
1、除号变乘号
2、前面不变
3、后面求倒数
练习 The teaching process
例:
2
1
练习 The teaching process
例:
分数除法递等式运算 The teaching process
1、找到除号,带后面的数变成乘倒数。
2、变乘法后,有简便运算的按照乘法运算定律计算。
3、没有简便运算的按照运算顺序计算。
例:
练习 The teaching process
补充 The teaching process
分数除法的比较大小:
找相同。
剩余的数比较大小。
把比较结果反过来。
>
03
分数方程
Analysis of teaching
解分数方程 The teaching process
1、将所有X放到等号左边。
2、如果有多个X,按照分配律合并成一个。
3、依次消除X以外所有的数字,后算的先消除。
4、加法运算用减法消除,乘法运算用除法消除。
5、遇到(-X)时,利用X=被减数-差求解。
6、遇到(÷X)时,利用X=被除数÷商求解。
解分数方程 The teaching process
1、将所有X放等号左边。(同时减X,同时加X)
例:
解分数方程 The teaching process
2、多个X合并成一个。(分配律)
例:
解分数方程 The teaching process
3、消除X以外的所有数字。(用逆运算移项)
例:
解分数方程 The teaching process
4、遇到(-X)和(÷X)的情况。(用数学关系)
例:
移项思想 The teaching process
练习 The teaching process
04
解决问题
Analysis of teaching
解决问题 Teaching background
A
B
C
D
单位1问题
效率速度问题
和差比问题
复杂方程
解决问题 Teaching background
1、单位“1”问题
谁是谁的几分之几?
谁占谁的几分之几?
谁的几分之几是谁?
谁比谁多几分之几?
谁比谁少几分之几?
含有没单位的分数。
存在是占比关系。
单位“1”未知。
比较量已知。
单位“1”=比较量÷分数
练习 Teaching background
1、学校有 20 个足球,足球比篮球多1/4,篮球有多少个?
2、学校有 20 个足球,足球比篮球少1/5,篮球有多少个?
3、五年级有 270 人,是四年级人数的1/9,四年级有多少人?
4、五年级有 270 人,比四年级多1/4,四年级有多少人?
5、一种彩电, 现在每台售价 1800 元, 是原来售价的1/10, 原来每台售价多少元?
6、一种彩电, 现在每台售价 1800 元, 比原来降低了1/10, 原来每台售价多少元?
7、一个正方形的周长为3/5米,它的边长是多少?
8、一个长方形的面积是3平方米,长为2/3米,宽是多少?
解决问题 Teaching background
2、和差比问题
谁是谁的几分之几?
谁占谁的几分之几?
谁的几分之几是谁?
谁比谁多几分之几?
谁比谁少几分之几?
存在是占比关系。
单位“1”,比较量都未知。
已知和差关系。
设单位“1”为X,比较量为aX。
根据和差关系列方程。
根据问题解完整。
练习 Teaching background
1、一个长方形的周长是7/8米,长是宽的6倍,长宽分别是多少?
2、香蕉是苹果的1/3,苹果比香蕉多20千克,香蕉苹果各有多少?
3、香蕉是苹果的1/3,苹果和香蕉共40千克,香蕉苹果各有多少?
4、香蕉比苹果多1/3,香蕉有20千克,苹果有多少千克?
5、香蕉比苹果多1/3,苹果和香蕉共35千克,香蕉苹果各有多少?
6、香蕉比苹果少1/3,苹果和香蕉共50千克,香蕉苹果各有多少?
解决问题 Teaching background
3、效率问题
单独完成要多久?
单独行驶要多久?
单独完成要几次?
单独放满要多久?
单独放空要多久?
共同完成一项任务,单独完成时间。
将总量看成单位“1”。
效率=1/时间。
合作情况时间=需工作总量÷效率和。
放水情况时间=1÷效率差。
练习 Teaching background
1、一项工程,甲单独6天完成,乙单独8天完成,两队合作几天?
2、一项工程,甲单独4天完成,乙单独3天完成,合作几天一半?
3、一项工程,甲单独6天完成,乙单独4天完成,甲先做2天,剩下合作,这项工程共花了几天?
4、一批货,货车运要10趟,皮卡运要25趟,一起运,要几趟?
5、从A地到B地,轿车要4小时,卡车要8小时,对开,多久相遇?
6、一个水池,进水管开6小时放满,出水管开9小时排空,
一起开,多久放满水池?
解决问题 Teaching background
4、复杂方程问题
不属于任何上述问题。
涉及对象比较多。
存在等量条件,“正好”,“相当于”。
选取合适的对象作为单位“1”。
根据等量条件列方程。
练习 Teaching background
1、学校有男生240人,其中女生的3/4正好是男生的1/2,女生有多少人?
2、学校有学生500人,男生比女生的5/6多40人,男生女生各有多少人?
3、一本书,第一天看了这本书的1/5,第二天看了50页,这时剩下的比已经看了的多60页,这本书有多少页?
2
0
1
9
感谢聆听
欢迎提问
2
0
1
9
分数除法
课程大纲
Teaching Programme
倒数的认识
分数除法法则
分数方程
解决问题
01
倒数的认识
Teaching background
倒数的认识 Teaching background
乘积是1的两个数,互为倒数。
那么a、b互为倒数;
a是b的倒数,b是a的倒数。
注:① 互为倒数的两个数,可以是整数,也可以是分数,小数。
② 倒数是一种关系,不是一种数,不能说a是倒数,b是倒数。
③ “1”的倒数是它本身。
④ “0”没有倒数
练习 Teaching background
判断对错
1、因为a×b=1,所以a、b互为倒数。
2、因为a×b=1,所以a、b都是倒数。
3、因为a×b=1,所以a是b的倒数,b是a的倒数。
4、因为5×0.2=1,所以他们互为倒数。
6、因为0.5+0.5=1,所以他们互为倒数。
7、因为1的倒数是1,所以0的倒数是0.
( )
( )
( )
( )
( )
( )
求倒数 Teaching background
求倒数
整数的倒数
分数的倒数
小数的倒数
带分数的倒数
求倒数 Teaching background
整数的倒数:求3的倒数。
本身做分母,分子是1。
a的倒数是
求倒数 Teaching background
分数的倒数:求 的倒数。
分数的倒数就是,
分子分母倒过来。
的倒数是
1
1
1
1
求倒数 Teaching background
带分数的倒数:求 的倒数。
现将带分数化成假分数,
再求假分数的倒数。
7
10
求倒数 Teaching background
小数的倒数:求 的倒数。
现将小数化成分数,
再求分数的倒数。
4
3
求倒数 Teaching background
得到这个数的倒数
分子分母倒过来
先化成分数形式
补充 Teaching background
1、真分数的倒数是假分数,大于1,大于它本身。
2、假分数的倒数是真分数,小于1 ,小于它本身。
3、带分数的倒数是真分数,小于1,小于它本身。
4、大于1的数,倒数小于1,小于它本身。
6、小于1 的数,倒数大于1,大于它本身。
补充
02
分数除法
The teaching process
分数除法 The teaching process
除以一个数等于乘以这个数的倒数,零除外。
1、除号变乘号
2、前面不变
3、后面求倒数
练习 The teaching process
例:
2
1
练习 The teaching process
例:
分数除法递等式运算 The teaching process
1、找到除号,带后面的数变成乘倒数。
2、变乘法后,有简便运算的按照乘法运算定律计算。
3、没有简便运算的按照运算顺序计算。
例:
练习 The teaching process
补充 The teaching process
分数除法的比较大小:
找相同。
剩余的数比较大小。
把比较结果反过来。
>
03
分数方程
Analysis of teaching
解分数方程 The teaching process
1、将所有X放到等号左边。
2、如果有多个X,按照分配律合并成一个。
3、依次消除X以外所有的数字,后算的先消除。
4、加法运算用减法消除,乘法运算用除法消除。
5、遇到(-X)时,利用X=被减数-差求解。
6、遇到(÷X)时,利用X=被除数÷商求解。
解分数方程 The teaching process
1、将所有X放等号左边。(同时减X,同时加X)
例:
解分数方程 The teaching process
2、多个X合并成一个。(分配律)
例:
解分数方程 The teaching process
3、消除X以外的所有数字。(用逆运算移项)
例:
解分数方程 The teaching process
4、遇到(-X)和(÷X)的情况。(用数学关系)
例:
移项思想 The teaching process
练习 The teaching process
04
解决问题
Analysis of teaching
解决问题 Teaching background
A
B
C
D
单位1问题
效率速度问题
和差比问题
复杂方程
解决问题 Teaching background
1、单位“1”问题
谁是谁的几分之几?
谁占谁的几分之几?
谁的几分之几是谁?
谁比谁多几分之几?
谁比谁少几分之几?
含有没单位的分数。
存在是占比关系。
单位“1”未知。
比较量已知。
单位“1”=比较量÷分数
练习 Teaching background
1、学校有 20 个足球,足球比篮球多1/4,篮球有多少个?
2、学校有 20 个足球,足球比篮球少1/5,篮球有多少个?
3、五年级有 270 人,是四年级人数的1/9,四年级有多少人?
4、五年级有 270 人,比四年级多1/4,四年级有多少人?
5、一种彩电, 现在每台售价 1800 元, 是原来售价的1/10, 原来每台售价多少元?
6、一种彩电, 现在每台售价 1800 元, 比原来降低了1/10, 原来每台售价多少元?
7、一个正方形的周长为3/5米,它的边长是多少?
8、一个长方形的面积是3平方米,长为2/3米,宽是多少?
解决问题 Teaching background
2、和差比问题
谁是谁的几分之几?
谁占谁的几分之几?
谁的几分之几是谁?
谁比谁多几分之几?
谁比谁少几分之几?
存在是占比关系。
单位“1”,比较量都未知。
已知和差关系。
设单位“1”为X,比较量为aX。
根据和差关系列方程。
根据问题解完整。
练习 Teaching background
1、一个长方形的周长是7/8米,长是宽的6倍,长宽分别是多少?
2、香蕉是苹果的1/3,苹果比香蕉多20千克,香蕉苹果各有多少?
3、香蕉是苹果的1/3,苹果和香蕉共40千克,香蕉苹果各有多少?
4、香蕉比苹果多1/3,香蕉有20千克,苹果有多少千克?
5、香蕉比苹果多1/3,苹果和香蕉共35千克,香蕉苹果各有多少?
6、香蕉比苹果少1/3,苹果和香蕉共50千克,香蕉苹果各有多少?
解决问题 Teaching background
3、效率问题
单独完成要多久?
单独行驶要多久?
单独完成要几次?
单独放满要多久?
单独放空要多久?
共同完成一项任务,单独完成时间。
将总量看成单位“1”。
效率=1/时间。
合作情况时间=需工作总量÷效率和。
放水情况时间=1÷效率差。
练习 Teaching background
1、一项工程,甲单独6天完成,乙单独8天完成,两队合作几天?
2、一项工程,甲单独4天完成,乙单独3天完成,合作几天一半?
3、一项工程,甲单独6天完成,乙单独4天完成,甲先做2天,剩下合作,这项工程共花了几天?
4、一批货,货车运要10趟,皮卡运要25趟,一起运,要几趟?
5、从A地到B地,轿车要4小时,卡车要8小时,对开,多久相遇?
6、一个水池,进水管开6小时放满,出水管开9小时排空,
一起开,多久放满水池?
解决问题 Teaching background
4、复杂方程问题
不属于任何上述问题。
涉及对象比较多。
存在等量条件,“正好”,“相当于”。
选取合适的对象作为单位“1”。
根据等量条件列方程。
练习 Teaching background
1、学校有男生240人,其中女生的3/4正好是男生的1/2,女生有多少人?
2、学校有学生500人,男生比女生的5/6多40人,男生女生各有多少人?
3、一本书,第一天看了这本书的1/5,第二天看了50页,这时剩下的比已经看了的多60页,这本书有多少页?
2
0
1
9
感谢聆听
欢迎提问
