湘教版数学九上3.5相似三角形的应用课件(19张PPT)
文档属性
| 名称 | 湘教版数学九上3.5相似三角形的应用课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 114.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-06 13:07:39 | ||
图片预览






文档简介
课件19张PPT。 导入新课
1、若△ABC~△ , 你能说出哪些结论?相似三角形的性质有哪些?
2、你能根据哪些条件判定△ABC~△ ?相似三角形有哪些判定方法?
一、相似三角形性质的直接应用
例1、如图,已知在△ABC中,DE∥AB,DE=3,BC=7,根据性质回答问题:
(1)AD:AB
(2)S△ADE:S △ ABC
(3)S △ ADE:S 四边形 DBCE 例2、如图,AB是斜靠在墙壁上的长梯。梯脚B距墙80cm,梯上点D距墙70cm,BD长55cm,梯子AB的长( )A、440 B、400
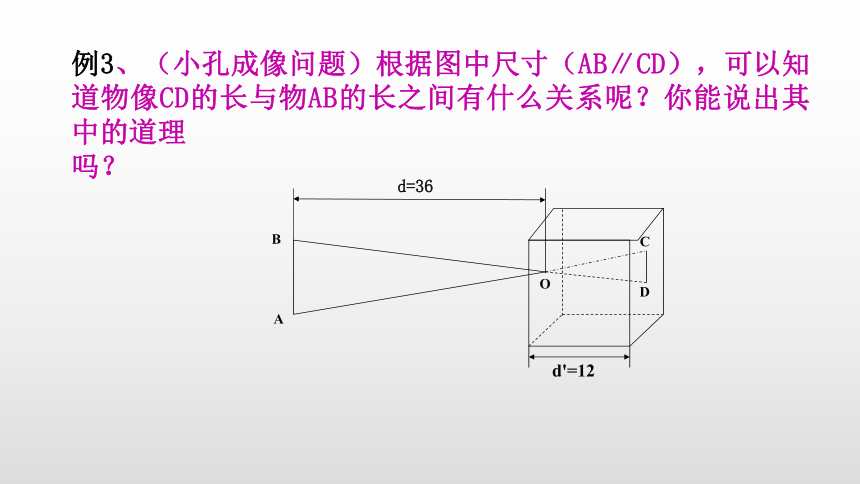
C、385 D、365A 例3、(小孔成像问题)根据图中尺寸(AB∥CD),可以知道物像CD的长与物AB的长之间有什么关系呢?你能说出其中的道理
吗?
二、相似三角形在动态问题中的应用 例1:在Rt△ABC中,A=90o,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,速度是每秒2个单位;动点E从点A出发,沿线段AC运动,每秒1个单位,两点同时出发,运动多长时间, △ ADE与 △ ABC相似?
解:∵△ ADE 与△ ABC相似
∴AE/AC=AD/AB
或AE/AB=AD/AC
设运动的时间是t秒,
则AE=t, AD=8-2t
∴t/6=8-2t/8或8-2t/6=t/8
解得:t=12/5或32/11
∴经过t=12/5或32/11秒两个三角形相似。 三、相似三角形在测量高度问题中的应用 例1:阳光明媚的一天,数学兴趣小组的同学去测量一棵树的高度(这棵树底部可以到达,顶部不可以到达),他们带了以下工具:皮尺,标杆,一副三角尺,小平面镜。请你在他们提供的工具中选出所需的工具,设计一种测量方案。(1)所需工具是( );
(2)请在下图中画出测量的示意图;
(3)设树高AB为x,请用所测数据(用小写字母表示)求出x。皮尺,标杆解:如图,测得标杆DE=a,树高和树影分别为AC=b,EF=c,
∵△DEF∽△ABC
∴ DE/BA=FE/CA
∴a/x=c/b ∴x=ab/c 例2: 如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB ⊥ BD,CD ⊥ BD, 且测得AB=1.2m,BP=1.8m, PD=12m,那么该古城墙的高度是( )CA、6米 B、8米 C、18米 D、24米B 例3:要测量旗杆的高度,在阳光下,一名同学测得一根1米长的标杆的影长0.4米,同时另一名同学测得旗杆高度时,发现影子不全落在地面上,有一部分落在教学楼上,测得影子长为2米,落在地面上的影子长为4.4米,则旗杆的高度为( )米。A、 10 B、 11 C 、 12 D、 13D 四、相似三角形在实际问题中的应用 例1:如图,阳光通过窗口照在室内(太阳光线是平行光线),在地面上留下2.7m宽的亮区,已知亮区到窗口下墙脚的距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.1.8解:由已知得,△CBD ∽△ CAE则
CB/CA=CD/CE
∴ CB/(CB+1.8)=(8.7-2.7)/8.7
解得:CB=4
∴窗口底边离地面的高度BC是4米。 如图,铁道口的栏杆的短臂长1米,长臂长16米,当短臂端点下降0.5米时,长臂端点升高( )(杆的宽度忽略不计)A7米 B8米 C9米 D10米B课堂练习 如图,在斜坡顶部有一铁塔AB,B 是CD的中点,CD是水平的,在阳光下,塔影DE留在坡面上,已知塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子落在坡面上,小华站在平地上,影子落在地面上,两人的影长分别为2米和1米,那么塔高AB为( )米。BA 24米 B 22米
C 20米 D 18米A 布置作业练习1、2、4 板书设计3.5相似三角形的应用一、相似三角形性质的直接应用
二、相似三角形在函数中的应用
三、相似三角形在动态问题中的应用四、相似三角形在测 量高度问题中的应用五、相似三角形在实际问题中的应用
1、若△ABC~△ , 你能说出哪些结论?相似三角形的性质有哪些?
2、你能根据哪些条件判定△ABC~△ ?相似三角形有哪些判定方法?
一、相似三角形性质的直接应用
例1、如图,已知在△ABC中,DE∥AB,DE=3,BC=7,根据性质回答问题:
(1)AD:AB
(2)S△ADE:S △ ABC
(3)S △ ADE:S 四边形 DBCE 例2、如图,AB是斜靠在墙壁上的长梯。梯脚B距墙80cm,梯上点D距墙70cm,BD长55cm,梯子AB的长( )A、440 B、400
C、385 D、365A 例3、(小孔成像问题)根据图中尺寸(AB∥CD),可以知道物像CD的长与物AB的长之间有什么关系呢?你能说出其中的道理
吗?
二、相似三角形在动态问题中的应用 例1:在Rt△ABC中,A=90o,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,速度是每秒2个单位;动点E从点A出发,沿线段AC运动,每秒1个单位,两点同时出发,运动多长时间, △ ADE与 △ ABC相似?
解:∵△ ADE 与△ ABC相似
∴AE/AC=AD/AB
或AE/AB=AD/AC
设运动的时间是t秒,
则AE=t, AD=8-2t
∴t/6=8-2t/8或8-2t/6=t/8
解得:t=12/5或32/11
∴经过t=12/5或32/11秒两个三角形相似。 三、相似三角形在测量高度问题中的应用 例1:阳光明媚的一天,数学兴趣小组的同学去测量一棵树的高度(这棵树底部可以到达,顶部不可以到达),他们带了以下工具:皮尺,标杆,一副三角尺,小平面镜。请你在他们提供的工具中选出所需的工具,设计一种测量方案。(1)所需工具是( );
(2)请在下图中画出测量的示意图;
(3)设树高AB为x,请用所测数据(用小写字母表示)求出x。皮尺,标杆解:如图,测得标杆DE=a,树高和树影分别为AC=b,EF=c,
∵△DEF∽△ABC
∴ DE/BA=FE/CA
∴a/x=c/b ∴x=ab/c 例2: 如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB ⊥ BD,CD ⊥ BD, 且测得AB=1.2m,BP=1.8m, PD=12m,那么该古城墙的高度是( )CA、6米 B、8米 C、18米 D、24米B 例3:要测量旗杆的高度,在阳光下,一名同学测得一根1米长的标杆的影长0.4米,同时另一名同学测得旗杆高度时,发现影子不全落在地面上,有一部分落在教学楼上,测得影子长为2米,落在地面上的影子长为4.4米,则旗杆的高度为( )米。A、 10 B、 11 C 、 12 D、 13D 四、相似三角形在实际问题中的应用 例1:如图,阳光通过窗口照在室内(太阳光线是平行光线),在地面上留下2.7m宽的亮区,已知亮区到窗口下墙脚的距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.1.8解:由已知得,△CBD ∽△ CAE则
CB/CA=CD/CE
∴ CB/(CB+1.8)=(8.7-2.7)/8.7
解得:CB=4
∴窗口底边离地面的高度BC是4米。 如图,铁道口的栏杆的短臂长1米,长臂长16米,当短臂端点下降0.5米时,长臂端点升高( )(杆的宽度忽略不计)A7米 B8米 C9米 D10米B课堂练习 如图,在斜坡顶部有一铁塔AB,B 是CD的中点,CD是水平的,在阳光下,塔影DE留在坡面上,已知塔底座宽CD=12米,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在点E处,影子落在坡面上,小华站在平地上,影子落在地面上,两人的影长分别为2米和1米,那么塔高AB为( )米。BA 24米 B 22米
C 20米 D 18米A 布置作业练习1、2、4 板书设计3.5相似三角形的应用一、相似三角形性质的直接应用
二、相似三角形在函数中的应用
三、相似三角形在动态问题中的应用四、相似三角形在测 量高度问题中的应用五、相似三角形在实际问题中的应用
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
