2019秋北师大版九年级数学上册第一章特殊平行四边形2矩形的性质与判定教学课件(共22张PPT)
文档属性
| 名称 | 2019秋北师大版九年级数学上册第一章特殊平行四边形2矩形的性质与判定教学课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-06 18:31:25 | ||
图片预览








文档简介
(共22张PPT)
教学课件
数学 九年级上册 北师大版
第一章 特殊平行四边形
1.2 矩形的性质与判定
1、能用综合法证明矩形的性质定理、判定定理以及相关结论;
2、能用矩形的性质进行简单的证明与计算.
请从边、角、对角线三个方面说一说平行四边形有哪些性质?
边:对边平行且相等;
角:对角相等;
对角线:对角线互相平分.
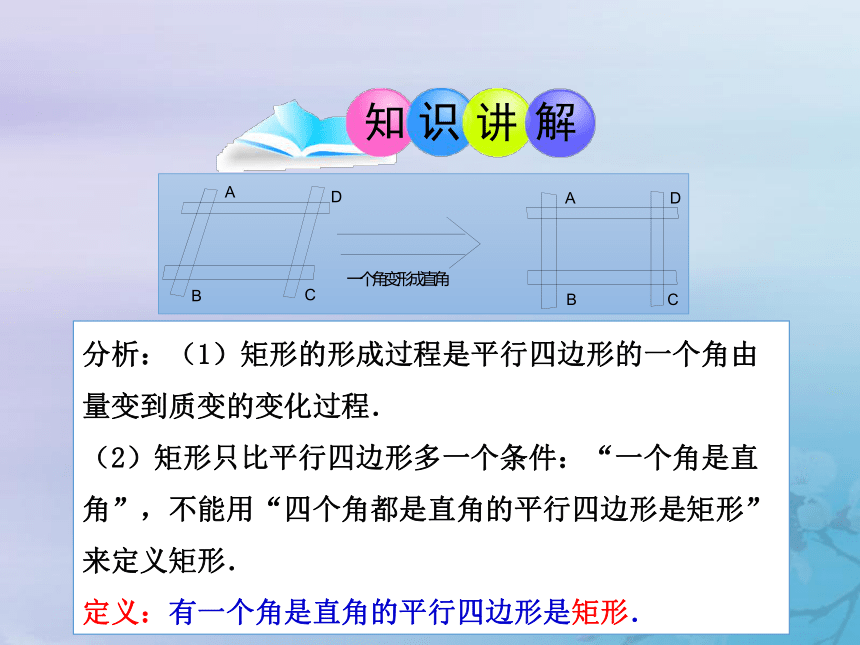
分析:(1)矩形的形成过程是平行四边形的一个角由量变到质变的变化过程.
(2)矩形只比平行四边形多一个条件:“一个角是直角”,不能用“四个角都是直角的平行四边形是矩形”来定义矩形.
定义:有一个角是直角的平行四边形是矩形.
矩形与平行四边形之间的关系
(3)矩形是特殊的平行四边形,具有平行四边形的一切性质(共性),还具有它自己特殊的性质(个性).
(4)从边、角、对角线方面,观察或度量猜想矩形的特殊性质.
①边:对边平行且相等(与平行四边形相同),邻边互相垂直;
②角:四个角是直角(性质1);
③对角线:相等且互相平分.
定理:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.
证明:
∵ 四边形ABCD是矩形.
∴∠A=90?,四边形ABCD是平行四边形.
∴∠C=∠A=90?,
∠B=180?-∠A=90?,
∠D=180?-∠A=90?.
求证:∠A=∠B=∠C=∠D=90?.
∴四边形ABCD是矩形.
定理:矩形的两条对角线相等.
已知:如图,AC,BD是矩形ABCD的两条对角线.
求证: AC=BD.
证明:
∵ 四边形ABCD是矩形.
∴AB=DC,∠ABC=∠DCB=90°.
分析:根据矩形的性质,可转化
为全等三角形(SAS)来证明.
∵BC=CB.
∴△ABC≌△DCB(SAS).
∴AC=DB.
推论:直角三角形斜边上的中线等于斜边的一半.
练一练:如图,在矩形ABCD中:
问:在Rt△ABC中,斜边AC上的中线是OB,它与斜边的关系是OB= AC.
问:是不是所有的三角形都有这样的性质? 关键是是不是任何一个三角形都可以放进一个矩形里?
【例1】已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=120°,AB=2.5cm.求矩形对角线的长.
解析:
∵四边形ABCD是矩形.
你认为例1还可以怎么去解?
定理:有三个角是直角的四边形是矩形.
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.
证明:
∵ ∠A=∠B=∠C=90°.
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
定理:对角线相等的平行四边形是矩形.
已知:如图,在□ABCD中,对角线AC=BD.
求证:平行四边形ABCD是矩形.
分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.
证明:
∴AB=CD,AB∥CD.
∵AC=DB,BC=CB.
∴ △ABC≌△DCB.
∴∠ABC=∠DCB.
∵四边形ABCD是平行四边形.
∵∠ABC+∠DCB=180°.
∴∠ABC=90°.
∴四边形ABCD是矩形.
下列各句判定矩形的说法是否正确?为什么?
(1)对角线相等的四边形是矩形;( )
(2)对角线互相平分且相等的四边形是矩形;( )
(3)有四个角是直角的四边形是矩形;( )
(4)对角线相等,且有一个角是直角的四边形是矩形;
( )
√
√
╳
╳
定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
求证:△ABC是直角三角形.
已知:CD是△ABC边AB上的中线,且
分析:要证明△ABC是直角三角形,可以将点A,B,C构造平行四边形,然后证明其对角线相等,即可证明是矩形.
证明:延长CD到E,使DE=DC,连接AE,BE.
∴四边形ACBE是平行四边形.
∵AB=2CD,CE=2CD.
∴ AC=DB.
∴四边形ACBE是矩形.
∵ AD=BD,CD=ED.
∴∠ACB=90°.
∴△ABC是直角三角形.
1.如图所示,已知□ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2,④AB⊥BC中,能说明□ABCD是矩形的有 (填写序号).
解析:根据对角线相等的平行四边形是矩形;矩形的定义.
答案:① ④
2.如图,在△ABC中,AB=AC=8,AD是底边上的高,E为AC的中点,则DE= .
解析:根据直角三角形斜边的中线等于斜边的一半可得,DE等于AC的一半,所以DE=4.
答案:4
3.如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.(1)求∠CAE的度数;
(2)取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.
解析:(1)在等边△ABC中,∵点D是BC边的中点,∴∠DAC=30?,又∵等边△ADE,∴∠DAE=60?,∴∠CAE=30?.
(2)在等边△ABC中,∵F是AB边的中点,D是BC边的中点,∴CF=AD,∠CFA=90?,又∵AD=AE,∴AE=CF,由(1)知∠CAE=30?,∴∠EAF=60?+30?=90?,∴∠CFA=∠EAF,∴CF∥AE,∵AE=CF,∴四边形AFCE是平行四边形,又∵∠CFA=90?,∴四边形AFCE是矩形.
4.已知:如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.
求证:四边形BMDN是矩形.
证明:在正三角形ABD和BCD中,M、N分别为BC、AD的中点.
∴BN⊥AD,DM⊥BC,∠DBC=60°,
∠BND=∠DMB=90°,∠NBD=30°.
∴∠NBM=90°.
∴四边形BMDN是矩形.
通过本课时的学习,需要我们掌握:
1、矩形的性质:
(1)矩形的四个角都是直角;
(2)矩形的对角线相等;
(3)推论:直角三角形斜边上的中线等于斜边的一半.
2、矩形的判定定理:
(1)定义:有一个角是直角的平行四边形是矩形;
(2)对角线相等的平行四边形是矩形;
(3)有三个角是直角的四边形是矩形.
3、直角三角形斜边上的中线等于斜边上的一半.
教学课件
数学 九年级上册 北师大版
第一章 特殊平行四边形
1.2 矩形的性质与判定
1、能用综合法证明矩形的性质定理、判定定理以及相关结论;
2、能用矩形的性质进行简单的证明与计算.
请从边、角、对角线三个方面说一说平行四边形有哪些性质?
边:对边平行且相等;
角:对角相等;
对角线:对角线互相平分.
分析:(1)矩形的形成过程是平行四边形的一个角由量变到质变的变化过程.
(2)矩形只比平行四边形多一个条件:“一个角是直角”,不能用“四个角都是直角的平行四边形是矩形”来定义矩形.
定义:有一个角是直角的平行四边形是矩形.
矩形与平行四边形之间的关系
(3)矩形是特殊的平行四边形,具有平行四边形的一切性质(共性),还具有它自己特殊的性质(个性).
(4)从边、角、对角线方面,观察或度量猜想矩形的特殊性质.
①边:对边平行且相等(与平行四边形相同),邻边互相垂直;
②角:四个角是直角(性质1);
③对角线:相等且互相平分.
定理:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.
证明:
∵ 四边形ABCD是矩形.
∴∠A=90?,四边形ABCD是平行四边形.
∴∠C=∠A=90?,
∠B=180?-∠A=90?,
∠D=180?-∠A=90?.
求证:∠A=∠B=∠C=∠D=90?.
∴四边形ABCD是矩形.
定理:矩形的两条对角线相等.
已知:如图,AC,BD是矩形ABCD的两条对角线.
求证: AC=BD.
证明:
∵ 四边形ABCD是矩形.
∴AB=DC,∠ABC=∠DCB=90°.
分析:根据矩形的性质,可转化
为全等三角形(SAS)来证明.
∵BC=CB.
∴△ABC≌△DCB(SAS).
∴AC=DB.
推论:直角三角形斜边上的中线等于斜边的一半.
练一练:如图,在矩形ABCD中:
问:在Rt△ABC中,斜边AC上的中线是OB,它与斜边的关系是OB= AC.
问:是不是所有的三角形都有这样的性质? 关键是是不是任何一个三角形都可以放进一个矩形里?
【例1】已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=120°,AB=2.5cm.求矩形对角线的长.
解析:
∵四边形ABCD是矩形.
你认为例1还可以怎么去解?
定理:有三个角是直角的四边形是矩形.
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.
证明:
∵ ∠A=∠B=∠C=90°.
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
定理:对角线相等的平行四边形是矩形.
已知:如图,在□ABCD中,对角线AC=BD.
求证:平行四边形ABCD是矩形.
分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.
证明:
∴AB=CD,AB∥CD.
∵AC=DB,BC=CB.
∴ △ABC≌△DCB.
∴∠ABC=∠DCB.
∵四边形ABCD是平行四边形.
∵∠ABC+∠DCB=180°.
∴∠ABC=90°.
∴四边形ABCD是矩形.
下列各句判定矩形的说法是否正确?为什么?
(1)对角线相等的四边形是矩形;( )
(2)对角线互相平分且相等的四边形是矩形;( )
(3)有四个角是直角的四边形是矩形;( )
(4)对角线相等,且有一个角是直角的四边形是矩形;
( )
√
√
╳
╳
定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
求证:△ABC是直角三角形.
已知:CD是△ABC边AB上的中线,且
分析:要证明△ABC是直角三角形,可以将点A,B,C构造平行四边形,然后证明其对角线相等,即可证明是矩形.
证明:延长CD到E,使DE=DC,连接AE,BE.
∴四边形ACBE是平行四边形.
∵AB=2CD,CE=2CD.
∴ AC=DB.
∴四边形ACBE是矩形.
∵ AD=BD,CD=ED.
∴∠ACB=90°.
∴△ABC是直角三角形.
1.如图所示,已知□ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2,④AB⊥BC中,能说明□ABCD是矩形的有 (填写序号).
解析:根据对角线相等的平行四边形是矩形;矩形的定义.
答案:① ④
2.如图,在△ABC中,AB=AC=8,AD是底边上的高,E为AC的中点,则DE= .
解析:根据直角三角形斜边的中线等于斜边的一半可得,DE等于AC的一半,所以DE=4.
答案:4
3.如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.(1)求∠CAE的度数;
(2)取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.
解析:(1)在等边△ABC中,∵点D是BC边的中点,∴∠DAC=30?,又∵等边△ADE,∴∠DAE=60?,∴∠CAE=30?.
(2)在等边△ABC中,∵F是AB边的中点,D是BC边的中点,∴CF=AD,∠CFA=90?,又∵AD=AE,∴AE=CF,由(1)知∠CAE=30?,∴∠EAF=60?+30?=90?,∴∠CFA=∠EAF,∴CF∥AE,∵AE=CF,∴四边形AFCE是平行四边形,又∵∠CFA=90?,∴四边形AFCE是矩形.
4.已知:如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.
求证:四边形BMDN是矩形.
证明:在正三角形ABD和BCD中,M、N分别为BC、AD的中点.
∴BN⊥AD,DM⊥BC,∠DBC=60°,
∠BND=∠DMB=90°,∠NBD=30°.
∴∠NBM=90°.
∴四边形BMDN是矩形.
通过本课时的学习,需要我们掌握:
1、矩形的性质:
(1)矩形的四个角都是直角;
(2)矩形的对角线相等;
(3)推论:直角三角形斜边上的中线等于斜边的一半.
2、矩形的判定定理:
(1)定义:有一个角是直角的平行四边形是矩形;
(2)对角线相等的平行四边形是矩形;
(3)有三个角是直角的四边形是矩形.
3、直角三角形斜边上的中线等于斜边上的一半.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
