北师大版初中数学七年级下册知识讲解,巩固练习(教学资料,补习资料):第14讲 全等三角形判定一(基础)含答案
文档属性
| 名称 | 北师大版初中数学七年级下册知识讲解,巩固练习(教学资料,补习资料):第14讲 全等三角形判定一(基础)含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 161.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-06 00:00:00 | ||
图片预览



文档简介
全等三角形判定一(SSS,ASA,AAS)(基础)
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,判定方法2——“角边角”,判定方法3——“角角边”;能运用它们判定两个三角形全等.
2.能把证明角相等或线段相等的问题,转化为证明它们所在的两个三角形全等.
【要点梳理】
要点一、全等三角形判定1——“边边边”
全等三角形判定1——“边边边”
三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
要点诠释:如图,如果/=AB,/=AC,/=BC,则△ABC≌△/.
/
要点二、全等三角形判定2——“角边角”
全等三角形判定2——“角边角”
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
要点诠释:如图,如果∠A=∠/,AB=/,∠B=∠/,则△ABC≌△/.
/
要点三、全等三角形判定3——“角角边”
1.全等三角形判定3——“角角边”
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
2.三个角对应相等的两个三角形不一定全等.
如图,在△ABC和△ADE中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC和△ADE不全等.这说明,三个角对应相等的两个三角形不一定全等.
/
要点四、如何选择三角形证全等
1.可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
2.可以从已知出发,看已知条件确定证哪两个三角形全等;
3.由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
4.如果以上方法都行不通,就添加辅助线,构造全等三角形.
【典型例题】
类型一、全等三角形的判定1——“边边边”
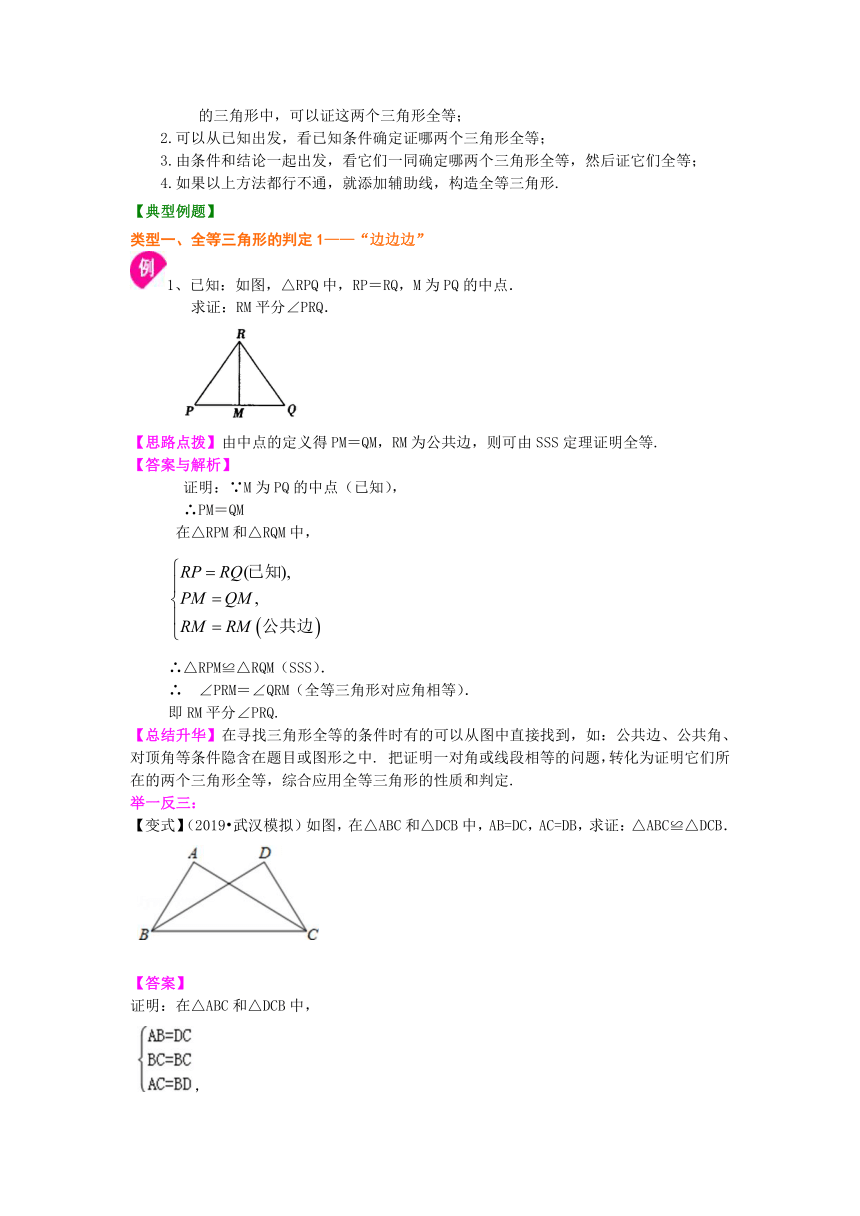
/1、已知:如图,△RPQ中,RP=RQ,M为PQ的中点.
求证:RM平分∠PRQ.
/
【思路点拨】由中点的定义得PM=QM,RM为公共边,则可由SSS定理证明全等.
【答案与解析】
证明:∵M为PQ的中点(已知),
∴PM=QM
在△RPM和△RQM中,
/
∴△RPM≌△RQM(SSS).
∴ ∠PRM=∠QRM(全等三角形对应角相等).
即RM平分∠PRQ.
【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.
举一反三:
【变式】(2019?武汉模拟)如图,在△ABC和△DCB中,AB=DC,AC=DB,求证:△ABC≌△DCB.
/
【答案】
证明:在△ABC和△DCB中,
/,
∴△ABC≌△DCB(SSS).
类型二、全等三角形的判定2——“角边角”
/2、(2019?安徽模拟)如图,点P在∠AOB的平分线上,若使△AOP≌△BOP,则需添加的一个条件是.
(1)小明添加的条件是:AP=BP.你认同吗?
(2)你添加的条件是 ,请用你添加的条件完成证明.
/
【思路点拨】(1)根据全等三角形的判定进行解答即可;(2)添加∠APO=∠BPO,利用ASA判断得出△AOP≌△BOP.
【答案】 (1)不认同;(2)∠APO=∠BPO.
【解析】
解:(1)不认同,按小明添加的条件,就是用“边边角”证明全等,而“边边角”是不能说明三角形全等的;
(2)∠APO=∠BPO.
理由:∵点P在∠AOB的平分线上,
∴∠AOP=∠BOP,
在△AOP和△BOP中
/,
∴△AOP≌△BOP(ASA).
故答案为:∠APO=∠BPO.
【总结升华】此题主要考查了全等三角形的判定,全等三角形的判定方法中,选用哪一种方法,取决于题目中的已知条件.
举一反三:
【变式】如图,AB∥CD,AF∥DE,BE=CF.求证:AB=CD.
/
【答案】
证明:∵AB∥CD,∴∠B=∠C.
∵AF∥DE,,∴∠AFB=∠DEC.
又∵BE=CF,∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
//
∴△ABF≌△DCE(ASA)
∴AB=CD(全等三角形对应边相等).
类型三、全等三角形的判定3——“角角边”
/3、已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.
求证:AD=AC.
/
【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.
【答案与解析】
证明:∵AB⊥AE,AD⊥AC,
∴∠CAD=∠BAE=90°
∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD
在△BAC和△EAD中
/
∴△BAC≌△EAD(AAS)
∴AC =AD
【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
举一反三:
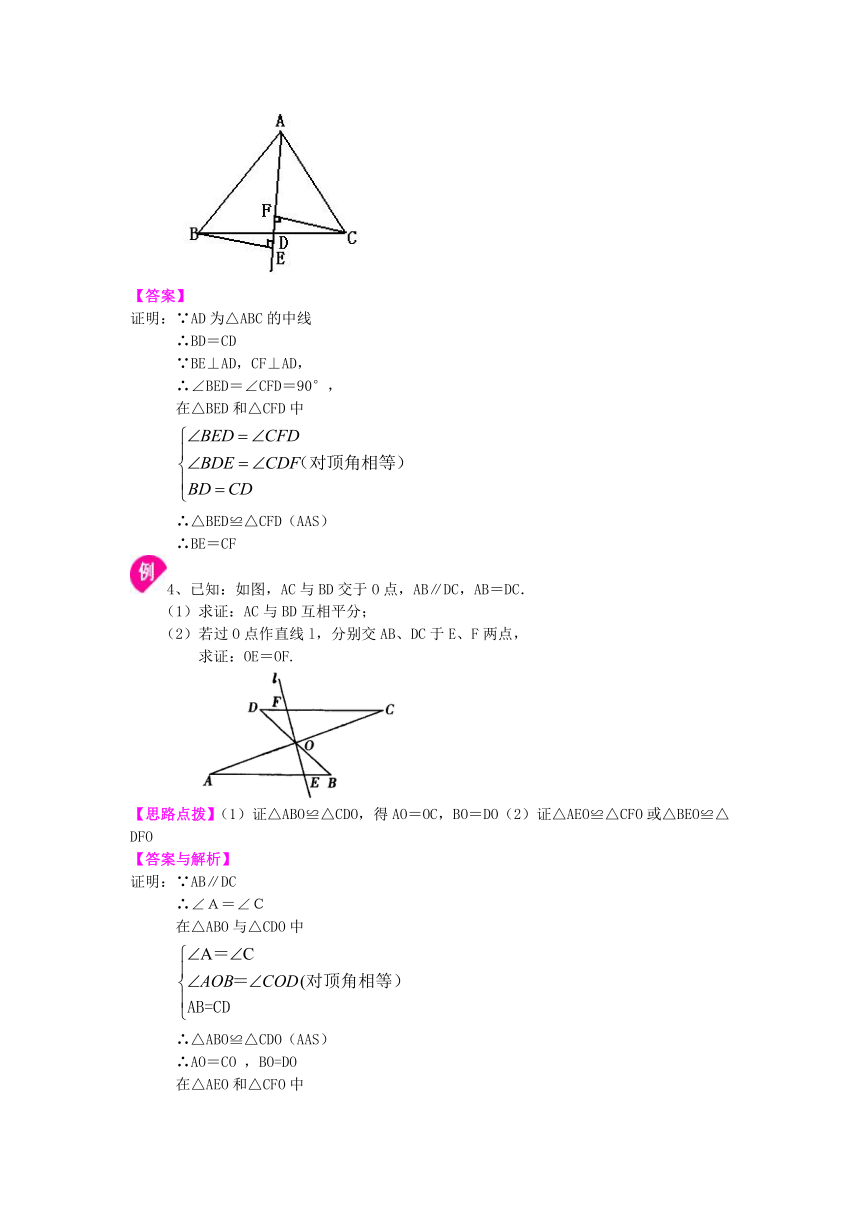
【变式】如图,AD是△ABC的中线,过C、B分别作AD及AD的延长线的垂线CF、BE.
求证:BE=CF.
/
【答案】
证明:∵AD为△ABC的中线
∴BD=CD ∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BED和△CFD中
/
∴△BED≌△CFD(AAS)
∴BE=CF
/4、已知:如图,AC与BD交于O点,AB∥DC,AB=DC.
(1)求证:AC与BD互相平分;
(2)若过O点作直线l,分别交AB、DC于E、F两点,
求证:OE=OF.
/
【思路点拨】(1)证△ABO≌△CDO,得AO=OC,BO=DO(2)证△AEO≌△CFO或△BEO≌△DFO
【答案与解析】
证明:∵AB∥DC
∴∠A=∠C
在△ABO与△CDO中
/
∴△ABO≌△CDO(AAS)
∴AO=CO ,BO=DO
在△AEO和△CFO中
/
∴△AEO≌△CFO(ASA)
∴OE=OF.
【总结升华】证明线段相等,就是证明它们所在的两个三角形全等.利用平行线找角等是本题的关键.
类型四、全等三角形判定的实际应用
/5、在一次战役中,我军阵地与敌军碉堡隔河相望,为了炸掉敌军的碉堡,要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,一名战士想出了这样一个办法:他面向碉堡站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部.然后,他转身向后,保持刚才的姿态,这时视线落在了自己这岸的某一点上.接着,他用步测的办法量出了自己与该点的距离,这个距离就是他与碉堡的距离.这名战士的方法有道理吗?请画图并结合图形说明理由.
【答案与解析】
/
设战士的身高为AB,点C是碉堡的底部,点D是被观测到的我军阵地岸上的点,由在观察过程中视线与帽檐的夹角不变,可知∠BAD=∠BAC,∠ABD=∠ABC=90°.
在△ABD和△ABC中,
/
∴△ABD≌△ABC(ASA)
∴BD=BC.
这名战士的方法有道理.
【总结升华】解决本题的关键是结合图形说明那名战士测出的距离就是阵地与碉堡的距离,可以先画出示意图,然后利用全等三角形进行说明.解决本题的关键是建立数学模型,将实际问题转化为数学问题并运用数学知识来分析和解决.
【巩固练习】
一、选择题
1. 能确定△ABC≌△DEF的条件是 ( )
A.AB=DE,BC=EF,∠A=∠E
B.AB=DE,BC=EF,∠C=∠E
C.∠A=∠E,AB=EF,∠B=∠D
D.∠A=∠D,AB=DE,∠B=∠E
2.(2019?杭州模拟)用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是( )
/
A. SSS B. SAS C. ASA D. AAS
3.AD是△ABC的角平分线,作DE⊥AB于E,DF⊥AC于F,下列结论错误的是( )
A.DE=DF B.AE=AF C.BD=CD D.∠ADE=∠ADF
4.(2019?黔西南州)如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
/
A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC
5. 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
/
6.如图,∠1=∠2,∠3=∠4,下面结论中错误的是( )
A.△ADC≌△BCD B.△ABD≌△BAC
C.△ABO≌△CDO D.△AOD≌△BOC
/
二、填空题
7.(2019秋?石林县校级月考)如图,AC=AD,BC=BD,则△ABC≌△ ;应用的判定方法是(简写) .
/
8. 在△ABC和△/中,∠A=44°,∠B=67°,∠/=69°,∠/=44°,且AC= /,则这两个三角形_________全等.(填“一定”或“不一定”)
9. 已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.
/
10. 如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对.
/
11.(2019?通州区一模)在学习“用直尺和圆规作射线OC,使它平分∠AOB”时,教科书介绍如下:*作法:(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
(2)分别以D,E为圆心,以大于/DE的同样长为半径作弧,两弧交于点C;
(3)作射线OC.
则OC就是所求作的射线.
小明同学想知道为什么这样做,所得到射线OC就是∠AOB的平分线.
小华的思路是连接DC、EC,可证△ODC≌△OEC,就能得到∠AOC=∠BOC.其中证明△ODC≌△OEC的理由是 .
/
12. 已知:如图,∠B=∠DEF,AB=DE,要说明△ABC≌△DEF,
(1)若以“ASA”为依据,还缺条件
(2)若以“AAS”为依据,还缺条件
/
三、解答题
13.阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB全等吗?若全等,试写出证明过程;若不全等,请说明理由.
答:△AOD≌△COB.
证明:在△AOD和△COB中,
/
∴ △AOD≌△COB (ASA).
问:这位同学的回答及证明过程正确吗?为什么?
14. 已知如图,E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:AC与BD互相平分. /
15. (2019秋?越秀区校级期中)已知:如图, AB∥CD, OA = OD, BC过O点, 点E、F在直线AOD上, 且∠E=∠F.
求证:EB=CF.
/
【答案与解析】
一.选择题
1. 【答案】D;
【解析】A、B选项是SSA,没有这种判定,C选项字母不对应.
2. 【答案】A;
【解析】从角平分线的作法得出,△AFD与△AED的三边全部相等,则△AFD≌△AED.
3. 【答案】C;
【解析】可由AAS证全等,得到A、B、D三个选项是正确的.
4. 【答案】C;
【解析】解:解:选项A、添加AB=DE可用AAS进行判定,故本选项错误;
选项B、添加AC=DF可用AAS进行判定,故本选项错误;
选项C、添加∠A=∠D不能判定△ABC≌△DEF,故本选项正确;
选项D、添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项错误.
故选C.
5. 【答案】C;
【解析】由ASA定理,可以确定△ABC.
6. 【答案】C;
【解析】△ABO与△CDO中,只能找出三对角相等,不能判定全等.
二、填空题
7. 【答案】ABD;SSS.
8. 【答案】一定;
【解析】由题意,△ABC≌△/,注意对应角和对应边.
9. 【答案】6;
【解析】△ABF≌△CDE,BE=CF=2,EF=10-2-2=6.
10.【答案】5;
【解析】△ABO≌△CDO,△AFO≌△CEO,△DFO≌△BEO,△AOD≌△COB,△ABD≌△CDB.
11.【答案】SSS;
【解析】解:由作法可知:CD=CE,OD=OE,
又∵OC=OC,
∴根据SSS可推出△OCD和△OCE全等,
故答案为:SSS.
12.【答案】(1)∠A=∠D;(2)∠ACB=∠F;
三、解答题
13. 【解析】
解: 这位同学的回答及证明过程不正确.
因为∠D所对的是AO,∠C所对的是OB,证明中用到了OA=OB,这不是一组对应边,所以不能由ASA去证明全等.
14.【解析】
证明: ∵BF=DE,
∴BF-EF=DE-EF,即BE=DF
在△ABE和△CDF中,
/
∴△ABE≌△CDF(SSS)
∴∠B=∠D,
在△ABO和△CDO中
/
∴△ABO≌△CDO(AAS)
∴AO=OC,BO=DO,AC与BD互相平分.
15.【解析】
证明:∵AB∥CD,
∴∠CDO=∠BAO
在△OAB和△ODC中,
/
∴△OAB≌△ODC(ASA)
∴OC=OB
在△OCF和△OBE中
/
∴△OCF≌△OBE(AAS)
∴EB=CF
【学习目标】
1.理解和掌握全等三角形判定方法1——“边边边”,判定方法2——“角边角”,判定方法3——“角角边”;能运用它们判定两个三角形全等.
2.能把证明角相等或线段相等的问题,转化为证明它们所在的两个三角形全等.
【要点梳理】
要点一、全等三角形判定1——“边边边”
全等三角形判定1——“边边边”
三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
要点诠释:如图,如果/=AB,/=AC,/=BC,则△ABC≌△/.
/
要点二、全等三角形判定2——“角边角”
全等三角形判定2——“角边角”
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
要点诠释:如图,如果∠A=∠/,AB=/,∠B=∠/,则△ABC≌△/.
/
要点三、全等三角形判定3——“角角边”
1.全等三角形判定3——“角角边”
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
2.三个角对应相等的两个三角形不一定全等.
如图,在△ABC和△ADE中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC和△ADE不全等.这说明,三个角对应相等的两个三角形不一定全等.
/
要点四、如何选择三角形证全等
1.可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;
2.可以从已知出发,看已知条件确定证哪两个三角形全等;
3.由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;
4.如果以上方法都行不通,就添加辅助线,构造全等三角形.
【典型例题】
类型一、全等三角形的判定1——“边边边”
/1、已知:如图,△RPQ中,RP=RQ,M为PQ的中点.
求证:RM平分∠PRQ.
/
【思路点拨】由中点的定义得PM=QM,RM为公共边,则可由SSS定理证明全等.
【答案与解析】
证明:∵M为PQ的中点(已知),
∴PM=QM
在△RPM和△RQM中,
/
∴△RPM≌△RQM(SSS).
∴ ∠PRM=∠QRM(全等三角形对应角相等).
即RM平分∠PRQ.
【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.
举一反三:
【变式】(2019?武汉模拟)如图,在△ABC和△DCB中,AB=DC,AC=DB,求证:△ABC≌△DCB.
/
【答案】
证明:在△ABC和△DCB中,
/,
∴△ABC≌△DCB(SSS).
类型二、全等三角形的判定2——“角边角”
/2、(2019?安徽模拟)如图,点P在∠AOB的平分线上,若使△AOP≌△BOP,则需添加的一个条件是.
(1)小明添加的条件是:AP=BP.你认同吗?
(2)你添加的条件是 ,请用你添加的条件完成证明.
/
【思路点拨】(1)根据全等三角形的判定进行解答即可;(2)添加∠APO=∠BPO,利用ASA判断得出△AOP≌△BOP.
【答案】 (1)不认同;(2)∠APO=∠BPO.
【解析】
解:(1)不认同,按小明添加的条件,就是用“边边角”证明全等,而“边边角”是不能说明三角形全等的;
(2)∠APO=∠BPO.
理由:∵点P在∠AOB的平分线上,
∴∠AOP=∠BOP,
在△AOP和△BOP中
/,
∴△AOP≌△BOP(ASA).
故答案为:∠APO=∠BPO.
【总结升华】此题主要考查了全等三角形的判定,全等三角形的判定方法中,选用哪一种方法,取决于题目中的已知条件.
举一反三:
【变式】如图,AB∥CD,AF∥DE,BE=CF.求证:AB=CD.
/
【答案】
证明:∵AB∥CD,∴∠B=∠C.
∵AF∥DE,,∴∠AFB=∠DEC.
又∵BE=CF,∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
//
∴△ABF≌△DCE(ASA)
∴AB=CD(全等三角形对应边相等).
类型三、全等三角形的判定3——“角角边”
/3、已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.
求证:AD=AC.
/
【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.
【答案与解析】
证明:∵AB⊥AE,AD⊥AC,
∴∠CAD=∠BAE=90°
∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD
在△BAC和△EAD中
/
∴△BAC≌△EAD(AAS)
∴AC =AD
【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.
举一反三:
【变式】如图,AD是△ABC的中线,过C、B分别作AD及AD的延长线的垂线CF、BE.
求证:BE=CF.
/
【答案】
证明:∵AD为△ABC的中线
∴BD=CD ∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BED和△CFD中
/
∴△BED≌△CFD(AAS)
∴BE=CF
/4、已知:如图,AC与BD交于O点,AB∥DC,AB=DC.
(1)求证:AC与BD互相平分;
(2)若过O点作直线l,分别交AB、DC于E、F两点,
求证:OE=OF.
/
【思路点拨】(1)证△ABO≌△CDO,得AO=OC,BO=DO(2)证△AEO≌△CFO或△BEO≌△DFO
【答案与解析】
证明:∵AB∥DC
∴∠A=∠C
在△ABO与△CDO中
/
∴△ABO≌△CDO(AAS)
∴AO=CO ,BO=DO
在△AEO和△CFO中
/
∴△AEO≌△CFO(ASA)
∴OE=OF.
【总结升华】证明线段相等,就是证明它们所在的两个三角形全等.利用平行线找角等是本题的关键.
类型四、全等三角形判定的实际应用
/5、在一次战役中,我军阵地与敌军碉堡隔河相望,为了炸掉敌军的碉堡,要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,一名战士想出了这样一个办法:他面向碉堡站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部.然后,他转身向后,保持刚才的姿态,这时视线落在了自己这岸的某一点上.接着,他用步测的办法量出了自己与该点的距离,这个距离就是他与碉堡的距离.这名战士的方法有道理吗?请画图并结合图形说明理由.
【答案与解析】
/
设战士的身高为AB,点C是碉堡的底部,点D是被观测到的我军阵地岸上的点,由在观察过程中视线与帽檐的夹角不变,可知∠BAD=∠BAC,∠ABD=∠ABC=90°.
在△ABD和△ABC中,
/
∴△ABD≌△ABC(ASA)
∴BD=BC.
这名战士的方法有道理.
【总结升华】解决本题的关键是结合图形说明那名战士测出的距离就是阵地与碉堡的距离,可以先画出示意图,然后利用全等三角形进行说明.解决本题的关键是建立数学模型,将实际问题转化为数学问题并运用数学知识来分析和解决.
【巩固练习】
一、选择题
1. 能确定△ABC≌△DEF的条件是 ( )
A.AB=DE,BC=EF,∠A=∠E
B.AB=DE,BC=EF,∠C=∠E
C.∠A=∠E,AB=EF,∠B=∠D
D.∠A=∠D,AB=DE,∠B=∠E
2.(2019?杭州模拟)用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是( )
/
A. SSS B. SAS C. ASA D. AAS
3.AD是△ABC的角平分线,作DE⊥AB于E,DF⊥AC于F,下列结论错误的是( )
A.DE=DF B.AE=AF C.BD=CD D.∠ADE=∠ADF
4.(2019?黔西南州)如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
/
A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC
5. 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
/
6.如图,∠1=∠2,∠3=∠4,下面结论中错误的是( )
A.△ADC≌△BCD B.△ABD≌△BAC
C.△ABO≌△CDO D.△AOD≌△BOC
/
二、填空题
7.(2019秋?石林县校级月考)如图,AC=AD,BC=BD,则△ABC≌△ ;应用的判定方法是(简写) .
/
8. 在△ABC和△/中,∠A=44°,∠B=67°,∠/=69°,∠/=44°,且AC= /,则这两个三角形_________全等.(填“一定”或“不一定”)
9. 已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.
/
10. 如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对.
/
11.(2019?通州区一模)在学习“用直尺和圆规作射线OC,使它平分∠AOB”时,教科书介绍如下:*作法:(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
(2)分别以D,E为圆心,以大于/DE的同样长为半径作弧,两弧交于点C;
(3)作射线OC.
则OC就是所求作的射线.
小明同学想知道为什么这样做,所得到射线OC就是∠AOB的平分线.
小华的思路是连接DC、EC,可证△ODC≌△OEC,就能得到∠AOC=∠BOC.其中证明△ODC≌△OEC的理由是 .
/
12. 已知:如图,∠B=∠DEF,AB=DE,要说明△ABC≌△DEF,
(1)若以“ASA”为依据,还缺条件
(2)若以“AAS”为依据,还缺条件
/
三、解答题
13.阅读下题及一位同学的解答过程:如图,AB和CD相交于点O,且OA=OB,∠A=∠C.那么△AOD与△COB全等吗?若全等,试写出证明过程;若不全等,请说明理由.
答:△AOD≌△COB.
证明:在△AOD和△COB中,
/
∴ △AOD≌△COB (ASA).
问:这位同学的回答及证明过程正确吗?为什么?
14. 已知如图,E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:AC与BD互相平分. /
15. (2019秋?越秀区校级期中)已知:如图, AB∥CD, OA = OD, BC过O点, 点E、F在直线AOD上, 且∠E=∠F.
求证:EB=CF.
/
【答案与解析】
一.选择题
1. 【答案】D;
【解析】A、B选项是SSA,没有这种判定,C选项字母不对应.
2. 【答案】A;
【解析】从角平分线的作法得出,△AFD与△AED的三边全部相等,则△AFD≌△AED.
3. 【答案】C;
【解析】可由AAS证全等,得到A、B、D三个选项是正确的.
4. 【答案】C;
【解析】解:解:选项A、添加AB=DE可用AAS进行判定,故本选项错误;
选项B、添加AC=DF可用AAS进行判定,故本选项错误;
选项C、添加∠A=∠D不能判定△ABC≌△DEF,故本选项正确;
选项D、添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项错误.
故选C.
5. 【答案】C;
【解析】由ASA定理,可以确定△ABC.
6. 【答案】C;
【解析】△ABO与△CDO中,只能找出三对角相等,不能判定全等.
二、填空题
7. 【答案】ABD;SSS.
8. 【答案】一定;
【解析】由题意,△ABC≌△/,注意对应角和对应边.
9. 【答案】6;
【解析】△ABF≌△CDE,BE=CF=2,EF=10-2-2=6.
10.【答案】5;
【解析】△ABO≌△CDO,△AFO≌△CEO,△DFO≌△BEO,△AOD≌△COB,△ABD≌△CDB.
11.【答案】SSS;
【解析】解:由作法可知:CD=CE,OD=OE,
又∵OC=OC,
∴根据SSS可推出△OCD和△OCE全等,
故答案为:SSS.
12.【答案】(1)∠A=∠D;(2)∠ACB=∠F;
三、解答题
13. 【解析】
解: 这位同学的回答及证明过程不正确.
因为∠D所对的是AO,∠C所对的是OB,证明中用到了OA=OB,这不是一组对应边,所以不能由ASA去证明全等.
14.【解析】
证明: ∵BF=DE,
∴BF-EF=DE-EF,即BE=DF
在△ABE和△CDF中,
/
∴△ABE≌△CDF(SSS)
∴∠B=∠D,
在△ABO和△CDO中
/
∴△ABO≌△CDO(AAS)
∴AO=OC,BO=DO,AC与BD互相平分.
15.【解析】
证明:∵AB∥CD,
∴∠CDO=∠BAO
在△OAB和△ODC中,
/
∴△OAB≌△ODC(ASA)
∴OC=OB
在△OCF和△OBE中
/
∴△OCF≌△OBE(AAS)
∴EB=CF
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
